 . Usually, we pick the notation that causes the least confusion.
. Usually, we pick the notation that causes the least confusion.In calculus, you’ll be asked to do two things: differentiate and integrate. In this section, you’re going to learn differentiation. Integration will come later, in the second half of this book. Before we go about the business of learning how to take derivatives, however, here’s a brief note about notation. Read this!
There are several different notations for derivatives in calculus. We’ll use two different types interchangeably throughout this book, so get used to them now.
We’ll refer to functions three different ways: f(x), u or v, and y. For example, we might write: f(x) = x3, g(x) = x4, h(x) = x5. We’ll also use notation like: u = sin x and v = cos x. Or we might use: y =  . Usually, we pick the notation that causes the least confusion.
. Usually, we pick the notation that causes the least confusion.
The derivatives of the functions will use notation that depends on the function, as shown in the following table:
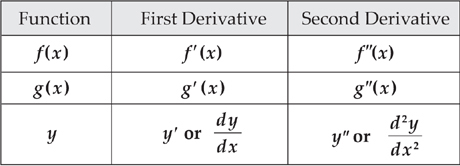
In addition, if we refer to a derivative of a function in general (for example, ax2 + bx + c), we might enclose the expression in parentheses and use either of the following notations:
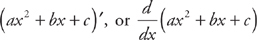
Sometimes math books refer to a derivative using either Dx or fx. We’re not going to use either of them.
In the last chapter, you learned how to find a derivative using the definition of the derivative, a process that is very time-consuming and sometimes involves a lot of complex algebra. Fortunately, there’s a shortcut to taking derivatives, so you’ll never have to use the definition again—except when it’s a question on an exam!
The basic technique for taking a derivative is called the Power Rule.
Rule No. 1: If y = xn, then 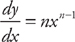
That’s it. Wasn’t that simple? Of course, this and all of the following rules can be derived easily from the definition of the derivative. Look at these next few examples of the Power Rule in action:
Example 1: If y = x5, then  .
.
Example 2: If y = x20, then 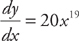 .
.
Example 3: If f(x) = x–5, then f′(x) = –5x–6.
When the power is a fraction, you should be careful to get the subtraction right (you’ll see the powers 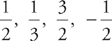 , and
, and 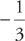 often, so be comfortable with subtracting 1 from them).
often, so be comfortable with subtracting 1 from them).
Example 4: If 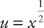 , then
, then 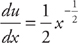 .
.
Example 5: If y = x1, then 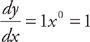 . (Because x0 is 1!)
. (Because x0 is 1!)
When the power is 0, the derivative is 0.
Example 6: If y = x0, then 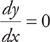 .
.
This leads to the next three rules:
Rule No. 2: If y = x, then  = 1
= 1
Rule No. 3: If y = kx, then  = k (where k is a constant)
= k (where k is a constant)
Rule No. 4: If y = k, then  = 0 (where k is a constant)
= 0 (where k is a constant)
Note: For future reference, a, b, c, n, and k always stand for constants.
Example 7: If y = 8x4, then  = 32x3.
= 32x3.
Example 8: If y = 5x100, then y′ = 500x99.
Example 9: If y = –3x–5, then  = 15x−6.
= 15x−6.
Example 10: If 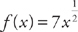 , then
, then 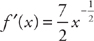 .
.
Example 11: If y = x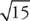 , then
, then  .
.
Example 12: If y = 12, then  = 0.
= 0.
If you have any questions about any of these 12 examples (especially the last two), review the rules. Now for one last rule.
If y = axn + bxm, where a and b are constants, then
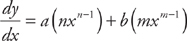
This works for subtraction, too.
Example 13: If y = 3x4 + 8x10, then  = 12x3 + 80x9.
= 12x3 + 80x9.
Example 14: If 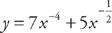 , then
, then  .
.
Example 15: If y = 5x4(2 – x3), then  = 40x3 − 35x6.
= 40x3 − 35x6.
Example 16: If y = (3x2 + 5)(x – 1), then

Example 17: If y = ax3 + bx2 + cx + d, then  = 3ax2 + 2bx + c.
= 3ax2 + 2bx + c.
After you’ve worked through all 17 of these examples, you should be able to take the derivative of any polynomial with ease.
As you may have noticed from the examples above, in calculus, you are often asked to convert from fractions and radicals to negative powers and fractional powers. In addition, don’t freak out if your answer doesn’t match any of the answer choices. Since answers to problems are often presented in simplified form, your answer may not be simplified enough.
There are two basic expressions that you’ll often be asked to differentiate. You can make your life easier by memorizing the following derivatives:

This may sound like a big deal, but it isn’t. This term refers only to taking the derivative of a function more than once. You don’t have to stop at the first derivative of a function; you can keep taking derivatives. The derivative of a first derivative is called the second derivative. The derivative of the second derivative is called the third derivative, and so on.
Generally, you’ll have to take only first and second derivatives.

Here are some sample problems involving the rules we discussed above. As you work, cover the answers with an index card, and then check your work after you’re done. By the time you finish them, you should know the rules by heart.
PROBLEM 1. If 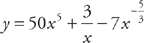 , then
, then 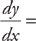
Answer: 
PROBLEM 2. If y = 9x4 + 6x2 – 7x + 11, then 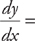
Answer:  = 9(4x3) + 6(2x) − 7(1) + 0 = 36x3 + 12x − 7
= 9(4x3) + 6(2x) − 7(1) + 0 = 36x3 + 12x − 7
PROBLEM 3. If 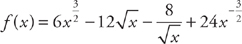 , then f′(x) =
, then f′(x) =
Answer: 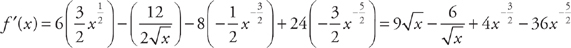
How’d you do? Did you notice the changes in notation? How about the fractional powers, radical signs, and x’s in denominators? You should be able to switch back and forth between notations, between fractional powers and radical signs, and between negative powers in a numerator and positive powers in a denominator.
Find the derivative of each expression and simplify. The answers are in Chapter 23.
1. (4x2 + 1)2
2. (x5 + 3x)2
3. 11x7
4. 8x10
5. 18x3 + 12x + 11
6.  (x12 + 17)
(x12 + 17)
7. − (x9 + 2x3 – 9)
(x9 + 2x3 – 9)
8. π5
10. –8x–8 + 12
11. 6x–7 – 4
14. (6x2 + 3)(12x – 4)
15. (3 – x – 2x3)(6 + x4)
16. e10 + π3 – 7
19. (x2 + 8x – 4)(2x–2 + x–4)
20. 0
21. (x + 1)3
23. x(2x + 7)(x – 2)
25. ax5 + bx4 + cx3 + dx2 + ex + f
Now that you know how to find derivatives of simple polynomials, it’s time to get more complicated. What if you had to find the derivative of this?
f(x) = (x3 + 5x2 – 4x + 1)(x5 – 7x4 + x)
You could multiply out the expression and take the derivative of each term, like this:
f(x) = x8 – 2x7 – 39x6 + 29x5 – 6x4 + 5x3 – 4x2 + x
And the derivative is:
f′(x) = 8x7 – 14x6 – 234x5 + 145x4 – 24x3 + 15x2 – 8x + 1
Needless to say, this process is messy. Naturally, there’s an easier way. When a function involves two terms multiplied by each other, we use the Product Rule.
The Product Rule: If f(x) = uv, then f′(x) = 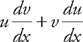
To find the derivative of two things multiplied by each other, you multiply the first function by the derivative of the second, and add that to the second function multiplied by the derivative of the first.
Let’s use the Product Rule to find the derivative of our example.
f′(x) = (x3 + 5x2 – 4x + 1)(5x4 – 28x3 + 1) + (x5 – 7x4 + x)(3x2 + 10x – 4)
If we were to simplify this, we’d get the same answer as before. But, here’s the best part: We’re not going to simplify it. One of the great things about the AP exam is that when it’s difficult to simplify an expression, you almost never have to. Nonetheless, you’ll often need to simplify expressions when you’re taking second derivatives, or when you use the derivative in some other equation. Practice simplifying whenever possible.
Example 1: f(x) = (9x2 + 4x)(x3 – 5x2)
f′(x) = (9x2 + 4x)(3x2 – 10x) + (x3 – 5x2)(18x + 4)
Example 2: 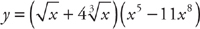
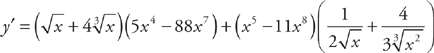
Example 3: 
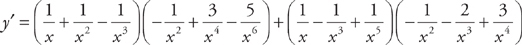
What happens when you have to take the derivative of a function that is the quotient of two other functions? You guessed it: Use the Quotient Rule.
The Quotient Rule:  , then
, then 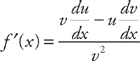
In this rule, as opposed to the Product Rule, the order in which you take the derivatives is very important, because you’re subtracting instead of adding. It’s always the bottom function times the derivative of the top minus the top function times the derivative of the bottom. Then divide the whole thing by the bottom function squared. A good way to remember this is to say the following:

You could also write:

Then you could derive the Quotient Rule using the Product Rule:
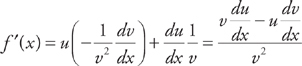
Here are some more examples:
Example 4: 
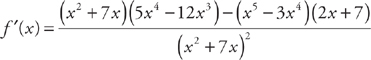

We’re not going to simplify these, although the Quotient Rule often produces expressions that simplify more readily than those involving the Product Rule. Sometimes it’s helpful to simplify, but avoid it otherwise. When you have to find a second derivative, however, you do have to simplify the quotient. If this is the case, the AP exam usually will give you a simple expression to deal with, such as in the example below.
Example 6: 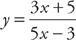
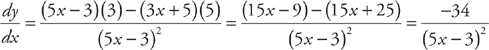
In order to take the derivative of  , you have to use the Chain Rule.
, you have to use the Chain Rule.
The most important rule in this chapter (and sometimes the most difficult one) is called the Chain Rule. It’s used when you’re given composite functions—that is, a function inside of another function. You’ll always see one of these on the AP exam, so it’s important to know the Chain Rule cold.
A composite function is usually written as: f(g(x)).
For example: f(x) =  and
and 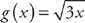 , then
, then 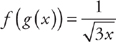
We could also find: 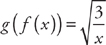
When finding the derivative of a composite function, we take the derivative of the “outside” function, with the inside function g considered as the variable, leaving the “inside” function alone. Then, we multiply this by the derivative of the “inside” function, with respect to its variable x.
Another way to write the Chain Rule is like this:
The Chain Rule: if y = f(g(x)), then 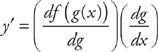
This rule is tricky, so here are several examples. The last couple incorporate the Product Rule and the Quotient Rule as well.
Example 7: If y = (5x3 + 3x)5, then  = 5(5x3 + 3x)4(15x2 + 3)
= 5(5x3 + 3x)4(15x2 + 3)
We just dealt with the derivative of something to the fifth power, like this:
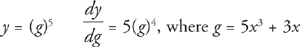
Then we multiplied by the derivative of g: (15x2 + 3).
Always do it this way. The process has several successive steps, like peeling away the layers of an onion until you reach the center.
Example 8: 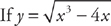 , then
, then 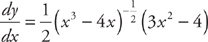
Again, we took the derivative of the outside function, leaving the inside alone. Then we multiplied by the derivative of the inside.
Example 9: If 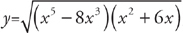 then
then
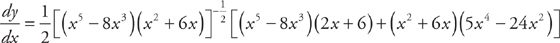
Messy, isn’t it? That’s because we used the Chain Rule and the Product Rule. Now for one with the Chain Rule and the Quotient Rule.
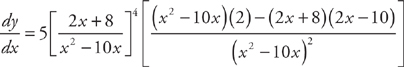
As you can see, these grow quite complex, so we simplify these only as a last resort. If you must simplify, the AP exam will have only a very simple Chain Rule problem.
Example 11: If 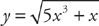 then
then 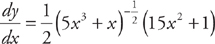
Now we use the Product Rule and the Chain Rule to find the second derivative:
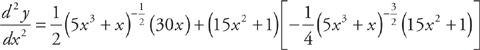
You can also simplify this further, if necessary.
There’s another representation of the Chain Rule that you need to learn.
If y = y(v) and v = v(x), then 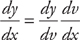
Example 12: y = 8v2 – 6v and v = 5x3 – 11x, then
 =(16v – 6)(15x2 – 11)
=(16v – 6)(15x2 – 11)
Then substitute for v:
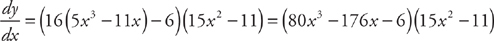
Here are some solved problems. Cover the answers first, then check your work.
PROBLEM 1. Find  if y = (5x4 + 3x7)(x10 − 8x).
if y = (5x4 + 3x7)(x10 − 8x).
Answer:  = (5x4 + 3x7)(10x9 − 8) + (x10 − 8x)(20x3 + 21x6)
= (5x4 + 3x7)(10x9 − 8) + (x10 − 8x)(20x3 + 21x6)
PROBLEM 2. Find  if y = (x3 + 3x2 + 3x + 1)(x2 + 2x + 1).
if y = (x3 + 3x2 + 3x + 1)(x2 + 2x + 1).
Answer:  = (x3 + 3x2 + 3x + 1)(2x + 2) + (x2 + 2x + 1)(3x2 + 6x + 3)
= (x3 + 3x2 + 3x + 1)(2x + 2) + (x2 + 2x + 1)(3x2 + 6x + 3)
PROBLEM 3. Find  if
if 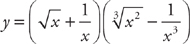 .
.
Answer: 
PROBLEM 4. Find  if
if 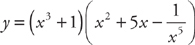 .
.
Answer: 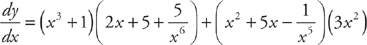
PROBLEM 5. Find  if
if  .
.
Answer: 
PROBLEM 6. Find  if
if 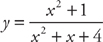 .
.
Answer: 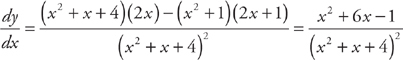
Answer: 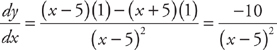
PROBLEM 8. Find  if y = (x4 + x)2.
if y = (x4 + x)2.
Answer:  = 2(x4 + x)(4x3 + 1)
= 2(x4 + x)(4x3 + 1)
PROBLEM 9. Find  if
if 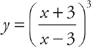 .
.
Answer: 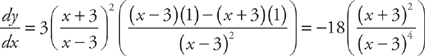
PROBLEM 10. Find  at x = 1 if
at x = 1 if 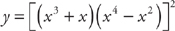 .
.
Answer: 
Once again, plug in right away. Never simplify until after you’ve substituted.
At x = 1,  = 0.
= 0.
Simplify when possible. The answers are in Chapter 23.
1. Find f′(x) if  .
.
2. Find f′(x) if f(x) = (x2 − 4x + 3)(x + 1).
3. Find f′(x) if f(x) = (x + 1)10.
4. Find f′(x) if  .
.
5. Find f′(x) if 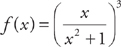 .
.
6. Find f′(x) if 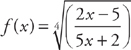 .
.
7. Find f′(x) if 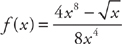 .
.
8. Find f′(x) if 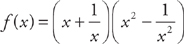 .
.
9. Find f′(x) if 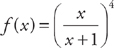 .
.
10. Find f′(x) if f(x) = (x2 + x)100.
11. Find f′(x) if 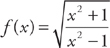 .
.
12. Find f′(x) at x = 2 if  .
.
13. Find f′(x) at x = 1 if 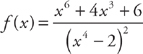 .
.
14. Find f′(x) at x = 1 if 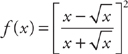 .
.
15. Find f′(x) if 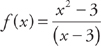 .
.
16. Find f′(x) at x = 1 if f(x) = (x4 − x2)(2x3 + x).
17. Find f′(x) at x = 2 if 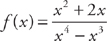 .
.
18. Find f′(x) if 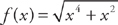 .
.
19. Find f′(x) at x = 1 if f(x) = 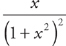 .
.
20. Find  if y = u2 − 1 and
if y = u2 − 1 and 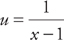 .
.
21. Find  at x = 1 if
at x = 1 if 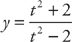 and t = x3.
and t = x3.
22. Find  if y = (x6 − 6x5)(5x2 + x) and x =
if y = (x6 − 6x5)(5x2 + x) and x =  .
.
23. Find 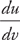 at v = 2 if
at v = 2 if 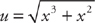 and
and  .
.
24. Find  at x = 1 if
at x = 1 if 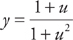 and u = x2 − 1.
and u = x2 − 1.
25. Find 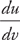 if u = y3 and
if u = y3 and  and x = v2.
and x = v2.
There are a lot of trigonometry problems in calculus and on the AP Calculus Exam. If you’re not sure of your trig, you should definitely go to the Appendix and review the unit on Prerequisite Math. You’ll need to remember your trig formulas, the values of the special angles, and the trig ratios, among other stuff.
In addition, angles are always referred to in radians. You can forget all about using degrees.
You should know the derivatives of all six trig functions. The good news is that the derivatives are pretty easy, and all you have to do is memorize them. Because the AP exam might ask you about this, though, let’s use the definition of the derivative to figure out the derivative of sin x.
If f(x) = sin x, then f(x + h) = sin(x + h).
Substitute this into the definition of the derivative:
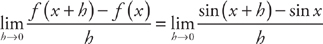
Remember that sin(x + h) = sin x cos h + cos x sin h. Now simplify it:
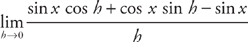
Next, rewrite this as:

Next, use some of the trigonometric limits that you memorized back in Chapter 3. Specifically:


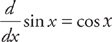
Example 1: Find the derivative of 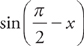 .
.
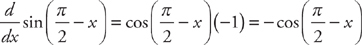
Use some of the rules of trigonometry you remember from last year. Because
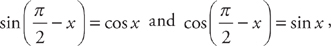
you can substitute into the above expression and get:

Now, let’s derive the derivatives of the other four trigonometric functions.
Example 2: Find the derivative of 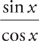 .
.
Use the Quotient Rule:
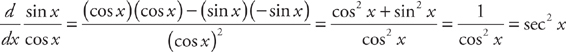
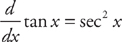
Example 3: Find the derivative of 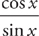 .
.
Use the Quotient Rule:

Because 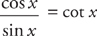 , you get:
, you get: 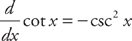 .
.
Example 4: Find the derivative of  .
.
Use the Reciprocal Rule.

Because 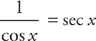 , you get:
, you get:
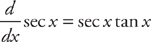
Example 5: Find the derivative of 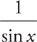 .
.
You get the idea by now.

Because 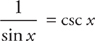 , you get:
, you get:

There you go. We have now found the derivatives of all six of the trigonometric functions. (A chart of them appears at the end of the book.) Now memorize them. You’ll thank us later.
Let’s do some more examples:
Example 6: Find the derivative of sin(5x).

Example 7: Find the derivative of sec(x2).
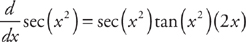
Example 8: Find the derivative of csc(x3 – 5x).
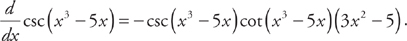
These derivatives are almost like formulas. You just follow the pattern and use the Chain Rule when appropriate.
Here are some solved problems. Do each problem, covering the answer first, then checking your answer.
PROBLEM 1. Find f′(x) if f(x) = sin(2x3).
Answer: Follow the rule: f′(x) = cos(2x3)6x2
PROBLEM 2. Find f′(x) if 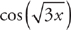 .
.
Answer: 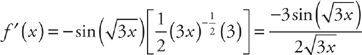
PROBLEM 3. Find f′(x) if 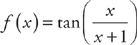 .
.
Answer: 
PROBLEM 4. Find f′(x) if f(x) = csc(x3 + x + 1).
Answer: Follow the rule: f′(x) = –csc(x3 + x + 1)cot(x3 + x + 1)(3x2 + 1)
Sometimes, we are given the graph of a function and we are asked to graph the derivative. We do this by analyzing the sign of derivative at various places on the graph and then sketching a graph of the derivative from that information. Let’s start with something simple. Suppose we have the graph of y = f(x) below and we are asked to sketch the graph of its derivative.
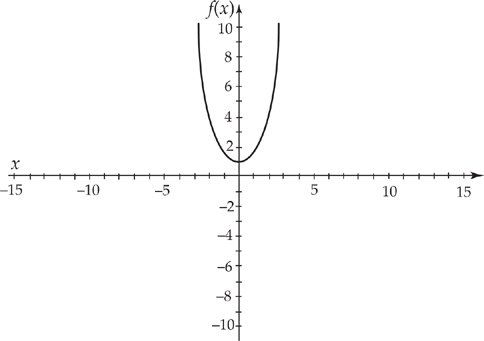
First, note that the derivative is zero at the point (0,1) because the tangent line is horizontal there. Next, the derivative is negative for all x < 0 because the tangent lines to the curve have negative slopes everywhere on the interval (–∞,0). Finally, the derivative is positive for all x > 0 because the tangent lines to the curve have positive slopes everywhere on the interval (0,∞). Now we can make a graph of the derivative. It will go through the origin (because the derivative is 0 at x = 0), it will be negative on the interval (–∞,0) and it will be positive on the interval (0,∞). The graph looks something like this:
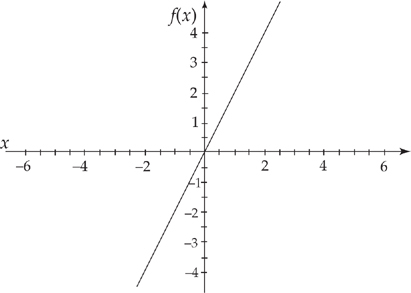
Now let’s try something a little harder. Suppose we have the following graph and we are asked to sketch the graph of the derivative:
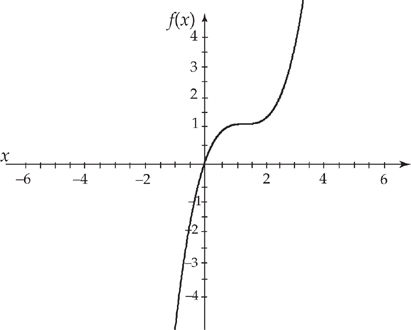
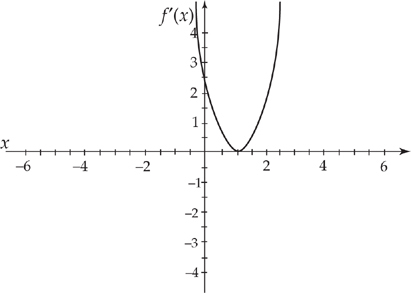
Notice that the tangent line looks as if it’s horizontal at x = 1. This means that the graph of the derivative is zero there. Next, the curve is increasing for all other values of x, so the graph of the derivative will be positive. As we go from left to right on the graph, notice that the slope starts out very steep, so the derivatives are large positive numbers. As we approach x = 1, the curve starts to flatten out, so the derivatives will approach zero but will still be positive. Then the slope is zero at x = 1. Then the curve gets steep again. If we sketch the derivative, we get something like this:
Here is an important one to understand. Suppose we have the graph of y = sin x:
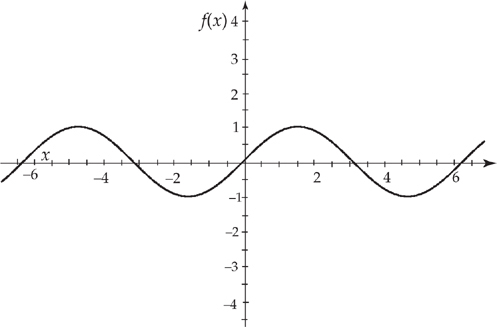
Notice that the slope of the tangent line will be horizontal at all of the maxima and minima of the graph. Because the slope of a horizontal line is zero, this means that the derivative will be zero at those values 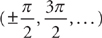 . Next, notice that the slope of the curve is about 1 as the curve goes through the origin. This should make sense if you recall that
. Next, notice that the slope of the curve is about 1 as the curve goes through the origin. This should make sense if you recall that  . The slope of the curve is about –1 as the curve goes through x = π. And so on. If we now sketch the derivative, it looks something like this:
. The slope of the curve is about –1 as the curve goes through x = π. And so on. If we now sketch the derivative, it looks something like this:
Notice that this is the graph of y = cos x. This should be obvious because the derivative of sin x is cos x.
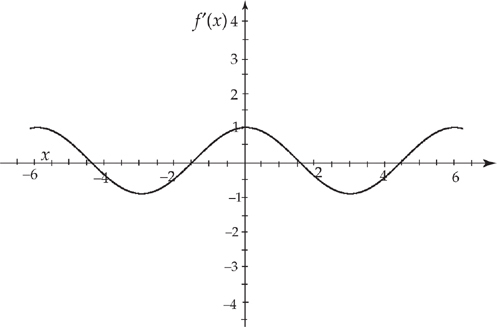
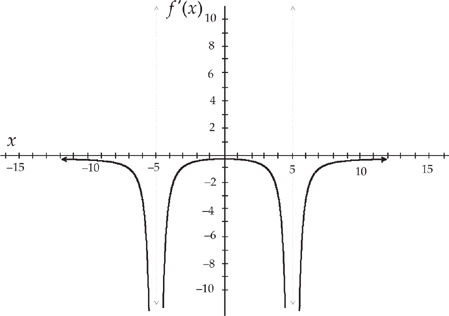
Now let’s do a hard one. Suppose we have the following graph:
First, notice that we have two vertical asymptotes at x = 6 and x = −6. This means that the graph of the derivative will also have vertical asymptotes at x = 6 and x = −6. Next, notice that the curve is always decreasing. This means that the graph of the derivative will always be negative. Moving from left to right, the graph starts out close to flat, so the derivative will be close to zero. Then the graph gets very steep and points downward, so the graph of the derivative will be negative and getting more negative. Then we have the asymptote x = −6. Next, the graph begins very steep and negative and starts to flatten out as we approach the origin. At the origin, the slope of the graph is approximately − . This means that the graph of the derivative will increase until it reaches
. This means that the graph of the derivative will increase until it reaches  . Then the graph starts to get steep again as we approach the other asymptote x = 6. Thus the graph will get more negative again. Finally, to the right of the asymptote x = 6 the graph starts out steep and negative and flattens out, approaching zero. This means that the graph of the derivative will start out very negative and will approach zero. If we now sketch the derivative, it looks something like this:
. Then the graph starts to get steep again as we approach the other asymptote x = 6. Thus the graph will get more negative again. Finally, to the right of the asymptote x = 6 the graph starts out steep and negative and flattens out, approaching zero. This means that the graph of the derivative will start out very negative and will approach zero. If we now sketch the derivative, it looks something like this:
Now try these problems. The answers are in Chapter 23.
1. Find  if y = sin2 x.
if y = sin2 x.
2. Find  if y = cos x2.
if y = cos x2.
3. Find  if y = (tan x)(sec x).
if y = (tan x)(sec x).
4. Find  if y = cot 4x.
if y = cot 4x.
5. Find  if
if 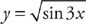 .
.
6. Find  if
if  .
.
7. Find  if y = csc2 x2.
if y = csc2 x2.
8. Find  if y = 2 sin 3x cos 4x.
if y = 2 sin 3x cos 4x.
9. Find  if y = sin 2x.
if y = sin 2x.
10. Find  if y = sin t – cos t and t = 1 + cos2 x.
if y = sin t – cos t and t = 1 + cos2 x.
11. Find  if
if 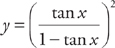 .
.
12. Find 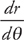 if r = secθ tan 2θ.
if r = secθ tan 2θ.
13. Find 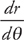 if r = cos(1 + sinθ).
if r = cos(1 + sinθ).
14. Find 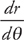 if
if 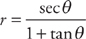 .
.
15. Find  if
if 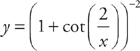 .
.
16. Find  if
if 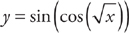 .
.