Chapter 11

Exponential and Logarithmic Functions, Part One

As with trigonometric functions, you’ll be expected to remember all of the logarithmic and exponential functions you’ve studied in the past. If you’re not sure about any of this stuff, review the unit on Prerequisite Mathematics. Also, this is only part one of our treatment of exponents and logs. Much of what you need to know about these functions requires knowledge of integrals (the second half of the book), so we’ll discuss them again later.

THE DERIVATIVE OF ln x

When you studied logs in the past, you probably concentrated on common logs (that is, those with a base of 10), and avoided natural logarithms (base e) as much as possible. Well, we have bad news for you: Most of what you’ll see from now on involves natural logs. In fact, common logs almost never show up in calculus. But that’s okay. All you have to do is memorize a bunch of rules, and you’ll be fine.

---

Rule No. 1: If y = ln x, then

---

This rule has a corollary that incorporates the Chain Rule and is actually a more useful rule to memorize:

---

Rule No. 2: If y = ln u, then

---

Remember: u is a function of x, and is its derivative.

You’ll see how simple this rule is after we try a few examples.

Example 1: Find the derivative of f(x) = ln(x³).

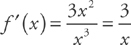
You could have done this another way. If you recall your rules of logarithms:

ln(x³) = 3 ln x

Therefore, .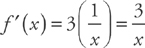

Example 2: Find the derivative of f(x) = ln(5x – 3x⁶).

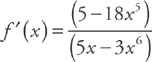
Example 3: Find the derivative of f(x) = ln(cos x).

Finding the derivative of a natural logarithm is just a matter of following a simple formula.

THE DERIVATIVE OF e^x

As you’ll see in Rule No. 3, the derivative of e^x is probably the easiest thing that you’ll ever have to do in calculus.

---

Rule No. 3: If y = e^x, then = e^x

---

That’s not a typo. The derivative is the same as the original function! Incorporating the Chain Rule, we get a good formula for finding the derivative:

---

Rule No. 4: If y = e^u, then

---

And you were worried that all of this logarithm and exponential stuff was going to be hard!

Example 4: Find the derivative of f(x) = e^3x.

f′(x) = e^3x(3) = 3e^3x

Example 5: Find the derivative of f(x) = e^x3.

f′(x) = e^x3(3x²) = 3x²e^x3

Example 6: Find the derivative of f(x) = e^tanx.

f(x) = (sec² x)e^{tan x}

Example 7: Find the second derivative of f(x) = e^x2.

f′(x) = 2xe^x2

f″(x) = 2e^x2 + 4x²e^x2

Once again, it’s just a matter of following a formula.

THE DERIVATIVE OF LOG_ax

This derivative is actually a little trickier than the derivative of a natural log. First, if you remember your logarithm rules about change of base, we can rewrite log_a x this way:

Review the unit on Prerequisite Mathematics if this leaves you scratching your head. Anyway, because ln a is a constant, we can take the derivative and we get:

This leads us to our next rule:

---

Rule No. 5: If y = log_ax, then

---

Once again, incorporating the Chain Rule gives us a more useful formula:

---

Rule No. 6: If y = log_au, then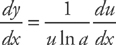

---

Example 8: Find the derivative of f(x) = log₁₀ x.

Note: We refer to
the log₁₀ x as log x.

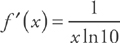
Example 9: Find the derivative of f(x) = log_a(x² + x).

Example 10: Find the derivative of f(x) = log_e x.

You can expect this result from Rules 1 and 2 involving natural logs.

THE DERIVATIVE OF a^x

You should recall from your precalculus days that we can rewrite a^x as e^{x ln a}. Keep in mind that ln a is just a constant, which gives us the next rule:

---

Rule No. 7: If y = a^x, then

---

Given the pattern of this chapter, you can guess what’s coming: another rule that incorporates the Chain Rule.

---

Rule No. 8: If y = a^u, then

---

And now, some examples:

Example 11: Find the derivative of f(x) = 3^x.

f′(x) = 3^x ln 3

Example 12: Find the derivative of f(x) = 8^4x5.

f′(x) = 8^4x5 (20x⁴) ln 8

Example 13: Find the derivative of f(x) = π^{sin x}.

f′(x) = π^{sin x} (cos x) ln π

Finally, here’s every nasty teacher’s favorite exponential derivative:

Example 14: Find the derivative of f(x) = x^x.

First, rewrite this as f(x) = e ^{x ln x}. Then take the derivative:

Would you have thought of that? Remember this trick. It might come in handy! Okay. Ready for some practice? Here are some more solved problems. Cover the solutions and get cracking.

PROBLEM 1. Find the derivative of y = 3ln(5x² + 4x).

Answer: Use Rule No. 2:

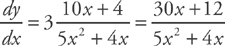
PROBLEM 2. Find the derivative of f(x) = ln(sin (x⁵)).

Answer:

PROBLEM 3. Find the derivative of f(x) = e^{3x7 − 4x2}.

Answer: Use Rule No. 4:

PROBLEM 4. Find the derivative of f(x) = log₄(tan x).

Answer: Use Rule No. 6:

PROBLEM 5. Find the derivative of .

Answer: First use the rules of logarithms to rewrite the equation:

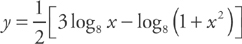
Now it’s much easier to find the derivative:

PROBLEM 6. Find the derivative of

Answer: Use Rule No. 8:

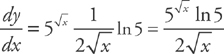
PROBLEM 7. Find the derivative of .

Answer: Here, you need to use the Quotient Rule and Rules Nos. 4 and 8:

PRACTICE PROBLEM SET 14

Now find the derivative of each of the following functions. The answers are in Chapter 23.

  1. f(x) = ln(x⁴ + 8)

  2.

  3. f(x) = ln(cot x − csc x)

  4. f(x) = x ln cos3x − x³

  5.

  6. f(x) = e^xcosx

  7. f(x) = e^−3x sin 5x

  8.

  9. f(x) = e^πx − ln e^πx

10. f(x) = log₁₂(x³)

11. f(x) = log₆(3x tan x)

12.

13.

14. f(x) = ln xlogx

15. f(x) = e^3x − 3^ex

16. f(x) = 10^sinx

17. f(x) = 5^tanx

18. f(x) = ln(10^x)

19. f(x) = x⁵5^x