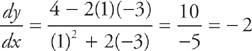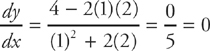Chapter 29

AB Calculus Practice Test 3 Answers and Explanations

ANSWER KEY TO SECTION 1

  1. B

  2. E

  3. B

  4. A

  5. B

  6. E

  7. D

  8. D

  9. A

10. C

11. C

12. B

13. B

14. A

15. D

16. E

17. D

18. C

19. D

20. B

21. C

22. A

23. D

24. D

25. B

26. B

27. E

28. A

29. A

30. C

31. B

32. D

33. A

34. B

35. C

36. C

37. E

38. A

39. B

40. D

41. D

42. C

43. E

44. B

45. B

ANSWERS AND EXPLANATIONS TO SECTION 1

  1. B

First, take the antiderivative:

Next, plug in x and 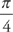for t and take the difference:

This can be simplified to .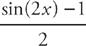

  2. E What are the coordinates of the point of inflection on the graph of y = x³ – 15x² + 33x + 100 ?

In order to find the inflection point(s) of a polynomial, we need to find the values of x where its second derivative is zero.

First, we find the first and second derivative:

Now, let’s set the second derivative equal to zero and solve for x:

6x – 30 = 0; x = 5

In order to find the y-coordinate, we plug in 5 for x in the original equation:

y = 5³ – 15(5²) + 33(5) + 100 = 15

Therefore, the coordinates of the point of inflection are (5, 15).

  3. B If 3x² – 2xy + 3y = 1, then when x = 2, =

We need to use implicit differentiation to find :

Now, if we wanted to solve for in terms of x and y, we would have to do some algebra to isolate . But, because we are asked to solve for at a specific value of x, we don’t need to simplify.

We need to find the y-coordinate that corresponds to the x-coordinate x = 2. We plug x = 2 into the original equation and solve for y:

Finally, we plug x = 2 and y = 11 into the derivative and we get:

  4. A

First, rewrite the integral as:

Using the power rule for integrals, which is 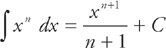, we get:

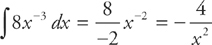
Next, plug in 3 and 1 for x and take the difference: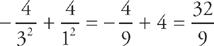

  5. B

The graph of a piecewise linear function f, for 0 ≤ x ≤ 8, is shown above. What is the value of ?

Here, we need to add the areas of the regions between the graph and the x-axis. Note that the area of the region between 0 and 5 has a positive value and the area of the region between 5 and 8 has a negative value. The area of the former region can be found by calculating the area of a trapezoid with bases of 2 and 5, and a height of 2. The area is (2 + 5)(2) = 7. The area of the latter region can be found by calculating the area of a triangle with a base of 3 and a height of 2. The area is (3)(2) = 3. Thus the value of the integral is 7 – 3 = 4.

  6. E If f is continuous for a ≤ x ≤ b, then at any point x = c, where a < c < b, which of the following must be true?

In order for f(x) to be continuous at a point c, there are three conditions that need to be fulfilled:

(1) f (c) exists

(2) exists

(3)

Answer choices (A), (B), (C), and (D) are not necessarily true.

  7. D If , then f′(x) =

Here we need to use the Product Rule, which is: If f(x) = uv, where u and v are both functions of x, then .

Here, we get:

This can be simplified to:

Multiply the numerator and denominator of the second expression by to get a common denominator:

This simplifies to:

  8. D What is the instantaneous rate of change at t = –1 of the function f, if ?

We find the instantaneous rate of change of the function by taking the derivative and plugging in t = –1.

We need to use the Quotient Rule, which is:

Given , then

Here, we have:

Next, plug in t = –1 and solve:

  9. A

You should know that .

We take the antiderivative and we get:

Next, plug in e + 1 and 2 for x and take the difference: 4 ln(e) – 4 ln(1)

You should know that lne = 1 and ln 1 = 0. Thus we get: 4 ln(e) – 4 ln(1) = 4

10. C

A car’s velocity is shown on the graph above. Which of the following gives the total distance traveled from t = 0 to t = 16 (in kilometers)?

We find the total distance traveled by finding the area of the region between the curve and the x-axis. Normally, we would have to integrate but here we can find the area of the region easily because it consists of geometric objects whose areas are simple to calculate.

The area of the region between t = 0 and t = 4 can be found by calculating the area of a triangle with a base of 4 and a height of 60. The area is (4)(60) = 120.

The area of the region between t = 4 and t = 8 can be found by calculating the area of a rectangle with a base of 4 and a height of 30.

The area is (4)(30) = 120.

The area of the region between t = 8 and t = 16 can be found by calculating the area of a trapezoid with bases of 4 and 8, and a height of 90 (or you could break it up into a rectangle and a triangle). The area is (4 + 8)(90) = 540.

Thus the total distance traveled is 120 + 120 + 540 = 780 kilometers.

11. C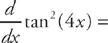

The derivative of . Here, we need to use the Chain Rule:

12. B What is the equation of the line tangent to the graph of y = sin² x at x = ?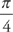

If we want to find the equation of the tangent line, first we need to find the y-coordinate that corresponds to x = 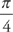. It is: .

Next, we need to find the derivative of the curve at x = 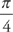, using the Chain Rule.

We get: = 2 sin x cos x. At x = , .

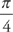Now we have the slope of the tangent line and a point that it goes through. We can use the point-slope formula for the equation of a line, (y – y₁) = m(x – x₁), and plug in what we have just found. We get: .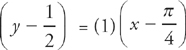

13. B If the function is differentiable for all real values of x, then b =

In order to solve this for b, we need f(x) to be differentiable at x = 1, which means that it must be continuous at x = 1. If we plug x = 1 into both pieces of this piecewise function, we get: , so we need 3a + 2b + 1 = a – 4b – 3, which can be simplified to 2a + 6b = –4.

Now, we take the derivative of both pieces of this function:

Then we plug in x = 1 and we get: , so we

need 6a + 2b = 4a – 8b – 3, which can be simplified to 2a + 10b = – 3

Solving the simultaneous equations, we get a = − and b = .

14. A The graph of y = x⁴ + 8x³ – 72x² + 4 is concave down for

A graph is concave down where the second derivative is negative.

First, we find the first and second derivative:

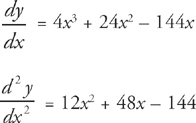
Next, we want to determine on which intervals the second derivative of the function is positive and on which it is negative. We do this by finding where the second derivative is zero:

12x² + 48x – 144 = 0
x² + 4x – 12 = 0
(x + 6)(x – 2) = 0
x = –6 or x = 2

We can test where the second derivative is positive and negative by picking a point in each of the three regions –∞ < x < –6, –6 < x < 2, and 2 < x < ∞, plugging the point into the second derivative, and seeing what the sign of the answer is. You should find that the second derivative is negative on the interval –6 < x < 2.

15. D If , then is

First, try plugging x = –8 into

We get: . This does NOT necessarily mean that the limit does not exist. When we get a limit of the form , we first try to simplify the function by factoring and canceling like terms. Here we get:

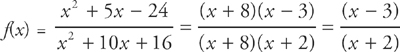
Now, if we plug in x = –8, we get: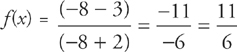

16. E

The graph of f(x) is shown in the figure above. Which of the following could be the graph of f′(x)?

Here we want to examine the slopes of various pieces of the graph of f(x). Notice that the graph has a positive slope from x = –∞ to x = –2, where the slope is zero. Thus we are looking for a graph of f′(x) that is positive from x = –∞ to x = –2 and zero at x = –2. Next, notice that the graph of f(x) has a negative slope from x = –2 to x = 2, where the slope is zero. Thus we are looking for a graph of f′(x) that is negative from x = –2 to x = 2 and zero at x = 2. Finally, notice that the graph of f(x) has a positive slope from x = 2 to x = ∞. Thus we are looking for a graph of f′(x) that is positive from x = 2 to x = ∞. Graph (E) satisfies all of these requirements.

17. D If f(x) = ln(cos(3x)), then f′(x) =

Remember that .

We will need to use the Chain Rule to find the derivative:

18. C If , then f′(–4)

The Second Fundamental Theorem of Calculus tells us how to find the derivative of an integral. It says that , where c is a constant and u is a function of x.

Here we can use the theorem to get:

Now we evaluate the expression at x = –4. We get: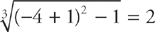

19. D A particle moves along the x-axis so that its position at time t, in seconds, is given by x(t) = t² – 7t + 6. For what value(s) of t is the velocity of the particle zero?

Velocity is the first derivative of position with respect to time.

The first derivative is: v(t) = 2t – 7.

Thus the velocity of the particle is zero at time t = 3.5 seconds.

20. B

We can use u-substitution to evaluate the integral.

Let u = sin² x and du = 2 sin x cos x dx. Next, recall from trigonometry that 2 sin x cos x = sin(2x). Now we can substitute into the integral 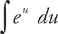, leaving out the limits of integration for the moment.

Evaluate the integral to get:

Now we substitute back to get: e^{sin2 x}

Finally, we evaluate at the limits of integration and we get:

21. C The average value of sec² x on the interval is

In order to find the average value, we use the Mean Value Theorem for integrals, which says that the average value of f(x) on the interval [a, b] is .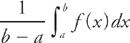

Here, we have .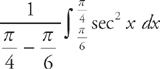

Next, recall that tan x = sec² x.

We evaluate the integral:

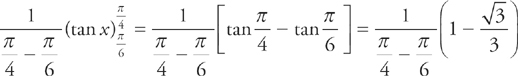
Get a common denominator for each of the two expressions:

We can simplify this to:

22. A Find the area of the region bounded by the parabolas y = x² and y = 6x – x².

First, we should graph the two curves:

Next, we need to find the points of intersection of the two curves, which we do by setting them equal to each other and solving for x:

x² = 6x – x²

2x² = 6x

2x² – 6x = 0

2x(x – 3) = 0

x = 0 or x = 3

We can find the area between the two curves by integrating the top curve minus the bottom curve, using the points of intersection as the limits of integration. We get:

We evaluate the integral and we get:

23. D The function f is given by f(x) = x⁴ + 4x³. On which of the following intervals is f decreasing?

A function is decreasing on an interval where the derivative is negative.

The derivative is f′(x) = 4x³ + 12x²

Next, we want to determine on which intervals the derivative of the function is positive and on which it is negative. We do this by finding where the derivative is zero:

4x³ + 12x² = 0

4x²(x + 3) = 0

x = –3 or x = 0

We can test where the derivative is positive and negative by picking a point in each of the three regions –∞ < x < –3, –3 < x < 0, and 0 < x < ∞, plugging the point into the derivative, and seeing what the sign of the answer is. Because x² is never negative, you should find that the derivative is negative on the interval –∞ < x < –3.

24. D

We will need to use the fact that to find the limit.

First, rewrite the limit as

Next, break the expression into two rational expressions:

Which can be broken up further into:

We will evaluate the limit of each separately.

First expression:

Divide the top and bottom by x: .

Then multiply the top and bottom of the upper expression by 3, and the top and bottom of the lower expression by 5: .

Now, if we take the limit, we get: .

Second expression:

This limit is straightforward:

Third expression:

First, pull the constant, 3, out of the limit: .

Now, if we multiply the top and bottom of the expression by 5, we get: .

Now, if we take the limit, we get: .

Combine the three numbers and we get: .

25. B If the region enclosed by the y-axis, the curve 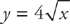, and the line y = 8 is revolved about the x-axis, the volume of the solid generated is

First, we graph the curves:

We can find the volume by taking a vertical slice of the region. The formula for the volume of a solid of revolution around the x-axis, using a vertical slice bounded from above by the curve f(x) and from below by g(x), on the interval [a, b], is:

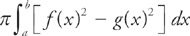
The upper curve is y = 8 and the lower curve is .

Next, we need to find the point(s) of intersection of the two curves, which we do by setting them equal to each other and solving for x:

Thus, the limits of integration are x = 0 and x = 4.

Now, we evaluate the integral:

26. B The maximum velocity attained on the interval 0 ≤ t ≤ 5 by the particle whose displacement is given by s(t) = 2t³ 12t² + 16t + 2 is

Velocity is the first derivative of position with respect to time.

The first derivative is:

v(t) = 6t² – 24t + 16

If we want to find the maximum velocity, we take the derivative of velocity (which is acceleration) and find where the derivative is zero:

v′(t) = 12t – 24

Next, we set the derivative equal to zero and solve for t, in order to find the critical value:

12t – 24 = 0

      t = 2

Note that the second derivative of velocity is 12, which is positive. Remember the second derivative test: If the sign of the second derivative at a critical value is positive, then the curve has a local minimum there. If the sign of the second derivative is negative, then the curve has a local maximum there.

Thus, the velocity is a minimum at t = 2. In order to find where it has an absolute maximum, we plug the endpoints of the interval into the original equation for velocity, and the larger value will be the answer.

At t = 0 the velocity is 16. At t = 5, the velocity is 46.

27. E The value of c that satisfies the Mean Value Theorem for derivatives on the interval [0, 5] for the function f(x) = x³ – 6x is

The Mean Value Theorem for derivatives says that, given a function f(x) which is continuous and differentiable on [a, b], then there exists some value c on (a, b) where .

Here, we have .

Plus, f′(c) = 3c² – 6, so we simply set 3c² – 6 = 19. If we solve for c, we get: . Both of these values satisfy the Mean Value Theorem for derivatives, but only the positive value, , is in the interval.

28. A If f(x) = sec(4x), then is

Recall that sec x = sec x tan x.

Therefore, using the Chain Rule, we get: f′(x) = 4 sec(4x) tan(4x)

If we plug in x = , we get:

29. A If f(x) is the function given by f(x) = e^3x + 1, at what value of x is the slope of the tangent line to f(x) equal to 2?

The slope of the tangent line is the derivative of the function. We get: f′(x) = 3e^3x. Now we set the derivative equal to 2 and solve for x.

Remember to round all answers to three decimal places on the AP exam.

30. C The graph of the function y = x³ + 12x² + 15x + 3 has a relative maximum at x =

First, let’s find the derivative: = 3x² + 24x + 15

Next, set the derivative equal to zero and solve for x.

3x² + 24x + 15 = 0

    x² + 8x + 5 = 0

Using the quadratic formula (or your calculator), we get:

Let’s use the second derivative test to determine which is the maximum. We take the second derivative and then plug in the critical values that we found when we set the first derivative equal to zero. If the sign of the second derivative at a critical value is positive, then the curve has a local minimum there. If the sign of the second derivative is negative, then the curve has a local maximum there.

The second derivative is: . The second derivative is negative at x = –7.317, so the curve has a local maximum there.

31. B The side of a square is increasing at a constant rate of 0.4 cm/sec. In terms of the perimeter, P, what is the rate of change of the area of the square, in cm²/sec?

The formula for the perimeter of a square is P = 4s, where s is the length of a side of the square.

If we differentiate this with respect to t, we get . We plug in and we get

The formula for the area of a square is A = s². If we solve the perimeter equation for s in terms of P and substitute it into the area equation we get:

If we differentiate this with respect to t, we get:

Now we plug in and we get:

32. D Let f be the function given by f(x) = 3x. For what value of x is the slope of the line tangent to the curve at (x, f (x)) equal to 1?

The slope of the tangent line is the derivative of the function.

Recall that a^x = a^x ln a. Here we get: f′(x) = 3^x ln 3

Now we set the derivative equal to 1 and solve for x.

Using the calculator, we get: 3^x ln 3 = 1

x ≈ –.086

33. A Given f and g are differentiable functions and

f(a) = –4, g(a) = c, g(c) =10, f (c) = 15

f′(a) = 8, g′(a) = b, g′(c) =5, f′(c) = 6

If h(x) = f (g(x)), find h′(a).

Use the Chain Rule to find h′(a) : h′(x) = f′(g(x))(g′(x))

We substitute a for x, and because g(a) = c, we get: h′(a) = f′(c)(g′(a)) = 6b

34. B What is the area of the region in the first quadrant enclosed by the graph of and the line y = 0.5?

First, we should graph the two curves:

Next, we need to find the points of intersection of the two curves, which we do by setting them equal to each other and solving for x.

You will need to use a calculator to solve for x. The answers are (to three decimal places): x = –1.665 and x = +1.665.

We can find the area between the two curves by integrating the top curve minus the bottom curve, using the points of intersection as the limits of integration. Because we want to find the area in the first quadrant, we use 0 as the lower limit of integration. We get:

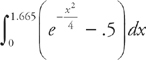
We will need a calculator to evaluate this integral:

35. C What is the trapezoidal approximation of using n = 4 subintervals?

The Trapezoid Rule enables us to approximate the area under a curve with a fair degree of accuracy. The rule says that the area between the x-axis and the curve y = f(x), on the interval [a, b], with n trapezoids, is:

Using the rule here, with n = 4, a = 0, and b = 3, we get:

36. C The second derivative of a function f is given by f″(x) = x sin x – 2. How many points of inflection does f have on the interval (–10, 10)?

Use your calculator to graph the second derivative and count the number of times that it crosses the x-axis on the interval (–10, 10):

It crosses four times, so there are four points of inflection.

37. E

Notice how this limit takes the form of the definition of the derivative, which is:

Here, if we think of f(x) as sin x, then this expression gives the derivative of sin x at the point .

The derivative of sin x is f′(x) = cos x. At , we get .

38. A

The Second Fundamental Theorem of Calculus tells us how to find the derivative of an integral: .

Here we can use the theorem to get:

39. B The base of a solid S is the region enclosed by the graph of 4x + 5y = 20, the x-axis, and the y-axis. If the cross-sections of S perpendicular to the x-axis are semicircles, then the volume of S is

First, sketch the region:

The rule for finding the volume of a solid with known cross-sections is , where A is the formula for the area of the cross-section. Here, x represents the diameter of a semi-circular cross-section.

The area of a semi-circle in terms of its diameter is . We find the length of the diameter by solving the equation 4x + 5y = 20 for y: . Next, we need to find where the graph intersects the x-axis. You should get x = 5. Thus, we find the volume by evaluating the integral:

This integral can be simplified to:

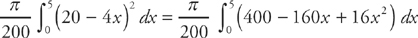
You can evaluate the integral by hand or with a calculator. You should get:

40. D Which of the following is an equation of the line tangent to the graph of y = x³ + x² at y = 3?

If we want to find the equation of the tangent line, first we need to find the x-coordinate that corresponds to y = 3. If you use your calculator to solve x³ + x² = 3, you should get x = 1.1746.

Next, we need to find the derivative of the curve at x = 1.1746.

We get:

(It is rounded to three decimal places.)

Now we have the slope of the tangent line and a point that it goes through. We can use the point-slope formula for the equation of a line, (y – y₁) = m(x – x₁) and plug in what we have just found. We get: (y – 3) = (6.488)(x – 1.1746). This simplifies to y = 6.488x – 4.620.

41. D If f′(x) = ln x – x + 2, at which of the following values of x does f have a relative minimum value?

Set the derivative equal to zero and solve for x. Using your calculator, you should get ln x – x + 2 = 0.

x = 3.146 or x = 0.159 (rounded to three decimal places)

Let’s use the second derivative test to determine which is the minimum. We take the second derivative and then plug in the critical values that we found when we set the first derivative equal to zero. If the sign of the second derivative at a critical value is positive, then the curve has a local minimum there. If the sign of the second derivative is negative, then the curve has a local maximum there.

The second derivative is: . The second derivative is positive at x = 0.159, so the curve has a local minimum there.

42. C Find the area of the region between the curve y = cos x and the x-axis from x = 1 to x = 2 radians.

First, we should graph the curve:

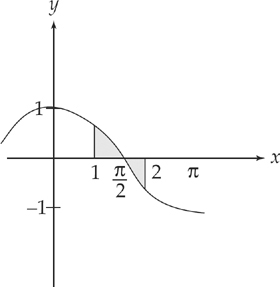
Note that the curve is above the x-axis from x = 1 to x = and below the x-axis from x = to x = 2. Thus, we need to evaluate two integrals to find the area:

We will need a calculator to evaluate these integrals:

43. E Let 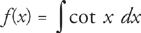; 0 < x < π. If 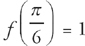, then f (1) =

We find by rewriting the integral as .

Then we use u-substitution. Let u = sin x and du = cos x.

Substituting, we can get: . Then substituting back, we get: ln(sin x) + C (We can get rid of the absolute value bars because sine is always positive on the interval).

Next, we use 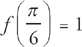to solve for C. We get:

Thus, f(x) = ln(sin x) + 1.693147

At x = 1, we get f(1) = ln(sin1) + 1.693147 = 1.521 (rounded to three decimal places).

44. B A radioactive isotope, y, decays according to the equation = ky, where k is a constant and t is measured in seconds. If the half-life of y is 1 minute, then the value of k is

We solve this differential equation using separation of variables.

First, move the y to the left side and the dt to the right side, to get: .

Now, integrate both sides:

ln y = kt + C

Next, it’s traditional to put the equation in terms of y. We do this by exponentiating both sides to the base e. We get: y = e^{kt + C}

Using the rules of exponents, we can rewrite this as: y = e^kt e^C. Finally, because e^C is a constant, we can rewrite the equation as: y = Ce^kt.

Now, we use the initial condition to solve for k. At time t = 60 (seconds), y = .

We are assuming a starting amount of y = 1, which will make C = 1. Actually, we could assume any starting amount. The half-life tells us that there will be half that amount after 1 minute. Therefore:

Solve for k:

This gives us: k = –0.012 (rounded to three decimal places)

45. B

Let 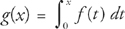, where f(t) has the graph shown above. Which of the following could be the graph of g?

The function is called an accumulation function and stands for the area between the curve and the x-axis to the point x. At x = 0, the area is 0, so g(0) = 0. From x = 0 to x = 2 the area grows, so g(x) has a positive slope. Then from x = 2 to x = 4 the area shrinks (because we subtract the area of the region under the x-axis from the area of the region above it), so g(x) has a negative slope. Finally, from x = 4 to x = 6 the area again grows, so g(x) has a positive slope. The curve that best represents this is (B).

ANSWERS AND EXPLANATIONS TO SECTION II

  1.

Let R be the region in the first quadrant shown in the figure above.

(a) Find the area of R.

(b) Find the volume of the solid generated when R is revolved about the x-axis.

(c) Find the volume of the solid generated when R is revolved about the line x = –1.

(a) In order to find the area, we “slice” the region vertically and add up all of the slices. We use the formula for the area of the region between y = f(x) and y = g(x), from x = a to x = b:

Here, we have:

f(x) = 4 – x² and g(x) = e^x

Next, we need to find the point of intersection in the first quadrant. Use your calculator to find that the point of intersection is x = 1.058 (rounded to three decimal places). Plugging into the formula, we get:

Evaluating the integral, we get:

(b) In order to find the volume of a region between y = f(x) and y = g(x), from x = a to x = b, when it is revolved about the x-axis, we use the formula:

Here our integral is:

Evaluating the integral, we get:

(c) In order to find the volume of this region, if we want to use vertical slices, we will use the method of cylindrical shells. Also, because we are revolving about the line x = –1, we will need to add 1 to the radius of the cylindrical shell. We will use the formula:

Here, we get:

We suggest that you use your calculator to evaluate the integral:

  2.    A body is coasting to a stop and the only force acting on it is a resistance proportional to its speed, according to the equation ; s(0) = 0, where v₀ is the body’s initial velocity (in m/s), v_f is its final velocity, m is its mass, k is a constant, and t is time.

(a) If a body, with mass m = 50 kg and k = 1.5 kg/sec, initially has a velocity of 30 m/s, how long, to the nearest second, will it take to slow to 1 m/s?

(b) How far, to the nearest 10 meters, will the body coast during the time it takes to slow from 30 m/s to 1 m/s?

(c) If the body coasts from 30 m/s to a stop, how far will it coast?

(a) We simply plug into the formula and solve for t.

We get:

Divide both sides by 30:

Take the log of both sides:

Multiply both sides by

(b) Now we need to solve the differential equation , which we can do with separation of variables.

First, multiply both sides by dt:

Integrate both sides:

Evaluate the integrals: .

Now plug in the initial conditions to solve for C:

Therefore, . Now we plug in the time t = 113 that we found in part (a) as well as the initial conditions to solve for is:

(c) Here, because the braking force is an exponential function, the object will coast to a stop after an infinite amount of time. In other words, we need to find:

  3.    An object moves with velocity v(t) = 9t² + 18t – 7 for t ≥ 0 from an initial position of s(0) = 3.

(a) Write an equation for the position of the particle.

(b) When is the particle changing direction?

(c) What is the total distance covered from t = 2 to t = 5?

(a) The position function of the particle can be determined by integrating the velocity with respect to time, thus s(t) = ∫v(t)dt. For this problem, s(t)= ∫ (9t² + 18t –7)dt = 3t³ + 9t² – 7t + C. Since we are given the initial position, s(0) = 3, plug that in to solve for C. Thus, C = 3 and the equation for the position of the particle is s(t) = 3t³ + 9t² – 7t + 3.

(b) The particle changes direction when the velocity is zero, but the acceleration is not. In order to determine when those times are, set the velocity equal to zero and solve for t. v(t) = 9t² + 18t – 7 = 0 when t = and t = –. Since, the time range in question is t ≥ 0, we can ignore t = –. Then, take the derivative of the velocity function to find the acceleration function, as (v(t)) = a(t). For the given v(t), a(t) = 18t + 18. Check that the acceleration at time t = is not zero by plugging into the acceleration function: a(t) = 30. Therefore, the particle is changing direction at t = because v(t) = 0 and a(t) ≠ 0.

(c) The distance covered is found by using the position function found in part (a). Determine the position at t = 2 and subtract it from the position at t = 5. From part (b), we know that the object does not change direction over this time interval, so we do not need to find the time piecewise. Thus, s(5) – s(2) = 568 – 49 = 519.

  4.

Three trains, A, B, and C, each travel on a straight track for 0 ≤ t ≤ 16 hours. The graphs above, which consist of line segments, show the velocities, in kilometers per hour, of trains A and B. The velocity of C is given by v(t) = 8t – 0.25t².

(Indicate units of measure for all answers.)

(a) Find the velocities of A and C at time t = 6 hours.

(b) Find the accelerations of B and C at time t = 6 hours.

(c) Find the positive difference between the total distance that A traveled and the total distance that B traveled in 16 hours.

(d) Find the total distance that C traveled in 16 hours.

(a) We can find the velocity of train A at time t = 6 simply by reading the graph. We get v_A(6) = 25 kph. We find the velocity of train C at time t = 6 by plugging t = 6 into the formula. We get v_C(6) = 8(6) – .25(6²) = 39 kilometers per hour.

(b) Acceleration is the derivative of velocity with respect to time. For train B, we look at the slope of the graph at time t = 6. We get: a_B(6) = 0 km/hr². For train C, we take the derivative of v. We get: a(t) = 8 – .5t. At time t = 6, we get a_C(6) = 5 km/hr².

(c) In order to find the total distance that train A traveled in 16 hours, we need to find the area under the graph. We can find this area by adding up the areas of the different geometric objects that are under the graph. From time t = 0 to t = 2, we need to find the area of a triangle with a base of 2 and a height of 20. The area is 20. Next, from time t = 2 to t = 4, we need to find the area of a rectangle with a base of 2 and a height of 20. The area is 40. Next, from time t = 4 to t = 8, we need to find the area of a trapezoid with bases of 20 and 30 and a height of 4. The area is 100. Next, from time t = 8 to t = 12, we need to find the area of a rectangle with a base of 4 and a height of 30. The area is 120. Finally, from time t = 12 to t = 16, we need to find the area of a triangle with a base of 4 and a height of 30. The area is 60. Thus the total distance that train A traveled is 340 km.

Let’s repeat the process for train B. From time t = 0 to t = 4, we need to find the area of a triangle with a base of 4 and a height of 40. The area is 80. Next, from time t = 4 to t = 10, we need to find the area of a rectangle with a base of 6 and a height of 40. The area is 240. Finally, from time t = 10 to t = 16, we need to find the area of a triangle with a base of 6 and a height of 40. The area is 120. Thus the total distance that train B traveled is 440 km.

Therefore, the positive difference between their distances is 100 km.

(d) First, note that the graph of train C ’s velocity, v(t) = 8t – 0.25t², is above the x-axis on the entire interval. Therefore, in order to find the total distance traveled, we integrate v(t) over the interval.

We get:

Evaluate the integral:

  5.    

The figure above shows the graph of g(x), where g is the derivative of the function f, for –3 ≤ x ≤ 9. The graph consists of three semicircular regions and has horizontal tangent lines at x = 0, x = 4.5, and x = 7.5.

(a) Find all values of x, for –3 < x ≤ 9, at which f attains a relative minimum. Justify your answer.

(b) Find all values of x, for –3 < x ≤ 9, at which f attains a relative maximum. Justify your answer.

(c) If , find f (6).

(d) Find all points where f″(x) = 0.

(a) Because g is the derivative of the function f, f will attain a relative minimum at a point where g = 0 and where g is negative to the left of that point and positive to the right of it. This occurs at x = 6.

(b) Because g is the derivative of the function f, f will attain a relative maximum at a point where g = 0 and where g is positive to the left of that point and negative to the right of it. This occurs at x = 3.

(c) We are trying to find the area between the graph and the x-axis from x = –3 to x = 6. From x = –3 to x = 3, the region is a semicircle of radius 3, so the area is .

From x = 3 to x = 6, the region is a semicircle of radius , so the area is . We subtract the latter region from the former to obtain: .

(d) Because f″(x) = g′(x), we are looking for points were the derivative of g is zero. This occurs at the horizontal tangent lines at x = 0, x = 4.5, and x = 7.5.

  6.    Consider the curve given by x²y – 4x + y² = 2.

(a) Find .

(b) Find .

(c) Find the equation of the tangent lines at each of the two points on the curve whose x-coordinate is 1.

(a) We can find by implicit differentiation:

Now we need to do some algebra to isolate . First, we move all of the terms that do not contain to the right side of the equals sign:

Next, we factor out : (x² + 2y) = 4 – 2xy

Finally, we divide through by (x² + 2y) to isolate :

(b) We need to use the Quotient Rule and implicit differentiation:

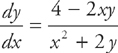Next, substitute into the derivative:

There is no need to simplify this.

(c) First, we need to find the y-coordinates that correspond to x = 1. We plug x = 1 into x²y – 4x + y² = 2, and rearrange a little, and we get: y² + y – 6 = 0.

Next, we factor the quadratic to get: (y + 3)(y – 2) = 0, so we will be finding tangent lines at the coordinates (1, –3) and (1, 2).

At (1, –3), we get:

Therefore, the equation of the tangent line is: y + 3 = –2(x – 1)

At (1, 2), we get:

Therefore, the equation of the tangent line is: y = 2