1. D If 7 = xy – exy, then  =
=
We need to use implicit differentiation to solve this problem.
Step 1: 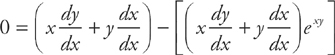 Remember:
Remember:  = 1
= 1
Step 2: 
Step 3: 
Step 4: 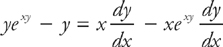
Step 5: 
Step 6: 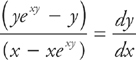
Step 7: 
2. B The volume of the solid that results when the area between the curve y = ex and the line y = 0, from x = 1 to x = 2, is revolved around the x-axis is
Step 1: We need to use the formula for finding the volume of a solid of revolution. The equations in the problems are given to us in terms of x, and we are rotating around the x-axis, so we can use the method of washers. The curve y = ex is always above the curve y = 0 (which is the x-axis), so we don’t have to break this up into two integrals.
Therefore, the integral will be: 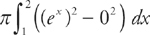
Step 2: 
Step 3: 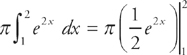
Step 4: 
Step 5: 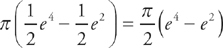
3. E 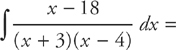
Step 1: We need to use partial fractions to evaluate this integral.
First, we write the integrand as: 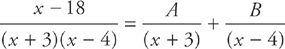
Step 2: Multiply both sides by: (x + 3) (x – 4)
Step 3: Now we have: x – 18 = A(x – 4) + B(x + 3)
Step 4: x – 18 = Ax – 4A + Bx + 3B
Step 5: x – 18 = (Ax + Bx) + (3B – 4A)
Step 6: x – 18 = x(A + B) + (3B – 4A)
Step 7: Thus: (A + B) = 1 and (3B – 4A) = –18
Step 8: Solve this using simultaneous equations to get: A = 3 and B = –2
Step 9: We can now rewrite the original integral as: 
Step 10: Which is the same as: 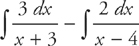
4. C If y = 5x2 + 4x and x = ln t then  =
=
We can solve this problem with the Chain Rule.
Step 1:  = 10x + 4
= 10x + 4
Step 2: 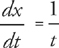
Step 3: 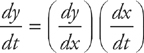 so
so 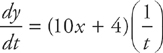
Step 4: Substitute for x so that 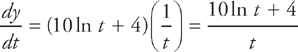
You could also have solved this by first substituting for x in the original equation and getting y in terms of t, and then differentiating with the Chain Rule.
5. A 
This trigonometric integral is solved by using u-substitution.
Step 1: Let 
Step 2: The integral is now written as: 
Note: The limits of integration change because:
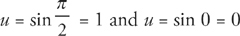
Step 3: 
Step 4: 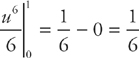
6. B The tangent line to the curve y = x3 – 4x + 8 at the point (2,8) has an x-intercept at
Step 1: First find the slope of the tangent line:  = 3x2 – 4
= 3x2 – 4
Step 2: Plug 2 into  = 3(2)2 – 4 = 12 – 4 = 8
= 3(2)2 – 4 = 12 – 4 = 8
This means that the slope of the tangent line at x = 2 is 8.
Step 3: Then the equation of the tangent line is (y – 8) = 8(x – 2).
Step 4: The x-intercept is found by plugging in y = 0 and solving for x:
0 – 8 = 8(x – 2)
Therefore, x = 1.
7. B The graph in the xy-plane represented by x = 3 sin(t) and y = 2 cos(t) is
This is a parametric equation and is solved by eliminating t from the equations and finding a direct relationship between y and x. These problems can often be quite difficult, but, fortunately, on the AP exam, they give only very easy versions of parametric equations.
Step 1:  = sin(t) and
= sin(t) and  = cos(t)
= cos(t)
Step 2: Because sin2 (t) + cos2 (t) = 1, we can substitute and we get  .
.
This is an ellipse.
8. E 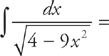
You should recognize this as an inverse trigonometric integral of the form  , which is sin–1 (u). You also should know this by looking at the answer choices. One of the difficulties of the AP exam is that you are required to recognize many different types of integrals by sight and then know which techniques to use to solve them.
, which is sin–1 (u). You also should know this by looking at the answer choices. One of the difficulties of the AP exam is that you are required to recognize many different types of integrals by sight and then know which techniques to use to solve them.
Step 1: First, we need to use a little algebra to convert the integrand to the form:

Rewrite: 
The integral then becomes: 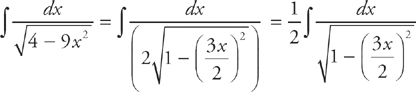
Step 2: Now we can use u-substitution. Let  and du =
and du =  dx and
dx and  du = dx.
du = dx.
We can now rewrite the integral as: 
Step 3: You should have memorized this last integral. It is: 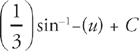
Step 4: Now reverse the u-substitution and we have:

9. C 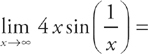
To solve this problem, you need to remember how to evaluate limits, particularly of trigonometric functions.
Step 1: As you should recall, the 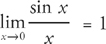 . (This can be shown with L’Hôpital’s Rule. Differentiate the top and bottom of the limit to obtain
. (This can be shown with L’Hôpital’s Rule. Differentiate the top and bottom of the limit to obtain  , which just equals 1.) Thus, we need to find a way to convert this integral into one that looks like
, which just equals 1.) Thus, we need to find a way to convert this integral into one that looks like  .
.
We can do this with a simple substitution. Let y =  . Now we can change this limit from
. Now we can change this limit from  .
.
Step 2: 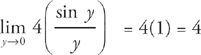
10. E The position of a particle moving along the x-axis at time t is given by x′(t) = ecos(2t), 0 ≤ t ≤ π. For which of the following values of t will x′(t) = 0?
This problem requires you to know derivatives of exponential functions and derivatives of trigonometric functions. Also, whenever you are given restrictions on the domain of a function, pay careful attention to the restrictions.
Step 1: x(t) = ecos(2t)(–2sin(2t))
Step 2: Now that we have the derivative, set it equal to zero:
ecos(2t)(–2sin(2t)) = 0
Step 3: Because ecos(2t) can never equal zero (Did you know this? Make sure that you do!), we only have to set –2sin(2t) equal to zero. This will be true wherever sin(2t) = 0. This will occur whenever 2t = 0, π, 2π,…or when t = 0,  , π,…Thus all three roman numeral answer choices work.
, π,…Thus all three roman numeral answer choices work.
11. B 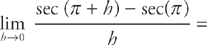
This may appear to be a limit problem, but it is actually testing to see whether you know the definition of the derivative.
Step 1: You should recall that  . Thus, if we replace f(x) with sec (x), we can rewrite the problem as:
. Thus, if we replace f(x) with sec (x), we can rewrite the problem as:

Step 2: The derivative of sec(x) is sec(x)tan(x). Thus,
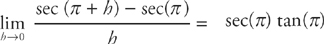
Step 3: Because sec(π) = –1 and tan(π) = 0, this is equal to 0.
12. C Use differentials to approximate the change in the volume of a cube when the side is decreased from 8 to 7.99 cm (in cm3).
The volume of a cube is V = x3. Using differentials, the change will be: dV = 3x2 dx
Substitute in x = 8 and dx = –.01, and we get:
dV = 3(82)(–.01)
dV = –1.92
13. C The radius of convergence of  ; a > 0 is
; a > 0 is
Step 1: An infinite series of the form  will converge if |r| < 1. So all we have to do is to set
will converge if |r| < 1. So all we have to do is to set 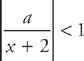 .
.
Step 2:  means that
means that 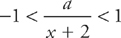 . We can rewrite this as
. We can rewrite this as  .
.
Step 3: Now we have – a > x + 2 > a or – a – 2 > x > a – 2.
14. C 
Step 1: Your first reaction to this integral may very well be “I don’t know how to find the integral of an inverse trigonometric function. I know only how to find the derivative of an inverse trigonometric function!” That’s okay. This is actually an integration by parts problem. First of all, we are going to ignore the limits of integration until the end of this problem, and just focus on finding the integral itself. As you should recall, the formula for integration by parts is:

Step 2: Let: u = sin–1 x and dv = dx.
Then:  and v = x
and v = x
Now, using integration by parts, we have: 
Step 3: We can now solve this latter integral with u-substitution.
Let u = 1 – x2 and du = –2x dx:

Then we have: 
Step 4: Substituting back for u gives us: 
Step 5: Now we evaluate at the limits of integration:
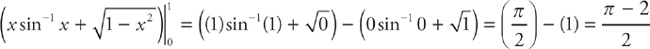
15. A The equation of the line normal to 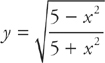 at x = 2 is
at x = 2 is
Step 1: This problem requires you to know how to find equations of tangent lines. We will use the point slope formula of a line: (y – y1) = m(x – x1).
x1 = 2 and y1 = 
Step 3:  This would now require some messy algebra to simplify, but fortunately we don’t have to. We can plug in 2 for x right now and solve for
This would now require some messy algebra to simplify, but fortunately we don’t have to. We can plug in 2 for x right now and solve for  , which simplifies to
, which simplifies to  .
.
Step 4: If we were finding the equation of a tangent line, we would use 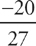 for m in the equation, but, as you should recall, because we are finding the equation of the normal line, we use the negative reciprocal of
for m in the equation, but, as you should recall, because we are finding the equation of the normal line, we use the negative reciprocal of 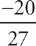 for m, which is
for m, which is 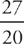 and plug it into the equation of the line.
and plug it into the equation of the line.
Step 5: Now we have (y – y1) = m(x – x1) which becomes 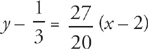 .
.
Multiply through by 60 to get: 60y – 20 = 81x – 162 or 81x – 60y = 142.
16. C If c satisfies the conclusion of the Mean Value Theorem for derivatives for f(x) = 2 sin x on the interval [0, π], then c could be
Step 1: The Mean Value Theorem for derivatives states that if a function is differentiable on an interval [a, b], then there exists some value c in that interval where 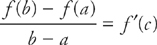
Step 2: 
Step 3: Thus f′(c) = 0. Because f′(c) = 2cos(c), we need to know what value of c makes 2 cos(c) = 0. The value is  .
.
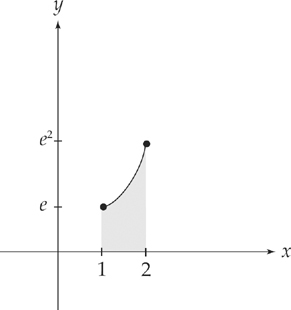
17. D The average value of f(x) = x ln x on the interval [1, e] is
This problem requires you to be familiar with the Mean Value Theorem for integrals, which we use to find the average value of a function.
Step 1: If you want to find the average value of f(x) on an interval [a, b], you need to evaluate the integral 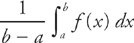 . So here we would evaluate the integral
. So here we would evaluate the integral 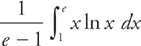 .
.
Step 2: We are going to need to do integration by parts to evaluate this integral. Let’s ignore the limits of integration for now and just do the integration:
Let u = ln x and dv = x dx.
Then: du =  dx and
dx and 
Now the integral becomes: 
Thus we have: 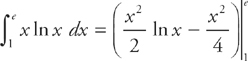
Step 3: 
This can be simplified to: 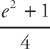
Step 4: Don’t forget to multiply by  . This gives the final result of:
. This gives the final result of: 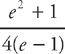 .
.
18. B A 17-foot ladder is sliding down a wall at a rate of –5 feet/sec. When the top of the ladder is 8 feet from the ground, how fast is the foot of the ladder sliding away from the wall (in feet/sec)?
Step 1: The ladder forms a right triangle with the wall, with the ladder itself as the hypotenuse. Whenever we see right triangles in related rates problems, we look to use the Pythagorean theorem.
Call the distance from the top of the ladder to the ground y, and the distance from the foot of the ladder to the wall x. Then the rate at which the top of the ladder is sliding down the wall is  , and the rate at which the foot of the ladder is sliding away from the wall is
, and the rate at which the foot of the ladder is sliding away from the wall is  , which is what we need to find. Now we use the Pythagorean Theorem to set up the relationships: x2 + y2 = 172
, which is what we need to find. Now we use the Pythagorean Theorem to set up the relationships: x2 + y2 = 172
Step 2: Differentiating both sides we obtain: 
Step 3: Because of the Pythagorean theorem, we also know that, when y = 8, x = 15.
Step 4: Now we plug everything into the equation from Step 2 and solve for  :
:

19. A If  = 3y cos x, and y = 8 when x = 0, then y =
= 3y cos x, and y = 8 when x = 0, then y =
Step 1: Separate the variables, by putting all of the terms containing y on the left hand side of the equals sign, and all of the terms containing x on the right hand side:

Step 2: Integrate both sides:
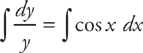
ln y = 3 sin x + C
Whenever we have a differential equation where the solution is in terms of ln y, we always solve the equation for y. This involves raising e to the power of each side. This gives us: eln y = e3 sin x + C; y = e3 sin x eC; y = Ce3 sin x. Now you should notice that eC is just a constant, so we call that C, and write the equation as:
y = Ce3 sin x
Step 3: Now plug in y = 8 and x = 0 in order to solve for C:
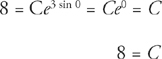
Step 4: This gives the final equation of y = 8e3 sin x.
20. E The length of the curve determined by x = 3t and y = 2t2 from t = 0 to t = 9 is
This problem requires you to find an Arc Length. This is a simple integral formula.
Step 1: The formula for the arc length of a curve given in parametric form on the interval [a, b] is:
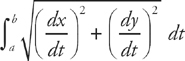
Step 2:  = 3 and
= 3 and  = 4t, so
= 4t, so 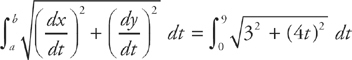
Step 3: 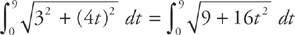
21. D If a particle moves in the xy-plane so that at time t > 0 its position vector is (et2, e−t3) then its velocity vector at time t = 3 is
This problem requires you to know how to find the velocity of a moving object.
Step 1: All you need to do to find the velocity of a moving object at a particular instant in time is to take the derivative of its position function at that time; the derivative of et2 = 2tet2 and the derivative of e−t3 = −3t2 e−t2.
Step 2: Now we plug in 3 for t and we get: 2tet2 = 6e9 and −3t2 e−t2 = −27 e−27
22. E The graph of 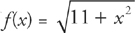 has a point of inflection at
has a point of inflection at
This problem requires you to know how to find the critical points on a graph, which is a crucial part of graphing functions.
Step 1: The points of inflection on a graph are generally at points where the second derivative is zero, but not necessarily at all points where the second derivative is zero. The good thing about the AP exam is that, in the multiple choice part of the test, you do not have to worry about exceptions to the second derivative rule. Thus, all we have to do here is to take the second derivative of the function and set it equal to zero:
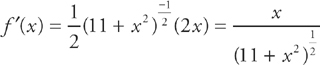
and

Step 2: When we are setting a rational function equal to zero, all we have to do is set the numerator equal to zero, and that value will be our point of inflection. Always double check that the value that makes the numerator equal to zero does not also make the DENOMINATOR equal to zero. If it does, this is NOT necessarily a point of inflection. Here, there is no point where 11 equals zero, so there is no point of inflection.
23. B What is the volume of the solid generated by rotating about the y-axis the region enclosed by y = sinx and the x-axis, from x = 0 to x = π?
This problem requires us to find the volume of a solid of revolution.
Step 1: Whenever you find the volume of a solid of revolution, you should first draw the graph of the equation so that you are sure of exactly what the curve looks like. You can graph this easily on your calculator, and should get something that looks like this:
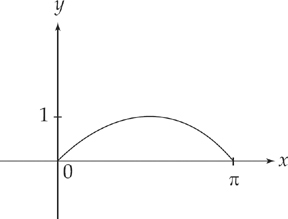
Step 2: Because we are revolving this curve around the y-axis, it will be easier to use the “shells” formula than the “washers” formula.
Using this formula, we get: 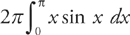 . This is one of our basic integration-by-parts integrals.
. This is one of our basic integration-by-parts integrals.
Let u = x and dv = sin x dx.
Then: du = dx and v = −–cos x
then,

Step 3: Now we evaluate at the limits of integration and we get:
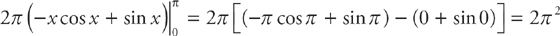
24. A 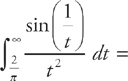
This is an improper integral. As with many of the more difficult topics in calculus, the AP examination tends to ask us to solve only very straightforward improper Integrals. The trick is to change the improper integral into a proper one.
Step 1: First, we need to rewrite the integral as a limit. Let a = ∞, and evaluate:
 . This gets rid of the “infinity problem.”
. This gets rid of the “infinity problem.”
At this point, we ignore the limits of integration while we figure out how to do the integral.
Using u-substitution, let 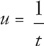 and
and 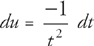 , which gives us:
, which gives us:  . Substituting back, we get
. Substituting back, we get 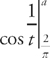
Step 2: Now we evaluate the integral at the limits of integration and get:

Step 3: Finally, we take the limit and we get: 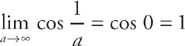
25. B A rectangle is to be inscribed between the parabola y = 4 – x2 and the x-axis, with its base on the x-axis. The value of x that maximizes the area of the rectangle is
This is a maximum/minimum problem. It is usually helpful to draw a picture first, so we know what we are looking for.
Step 1: If we graph y = 4 – x2 and sketch in a rectangle, we get something like this:
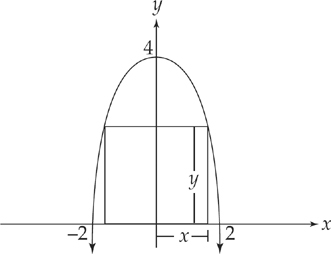
Step 2: Notice that the length of the base of the rectangle is 2x and the height of the rectangle is y. This means that the area of the rectangle is: A = 2xy. If we substitute
4 – x2 for y, we get: A = 2x(4 – x2) = 8x – 2x3.
Step 3: If we want to find the maximum area, all we have to do is take the derivative of A and set it equal to zero:
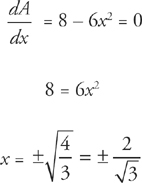
Because the answer is looking for a length, we are satisfied with the positive answer.
Besides,  isn’t an answer choice.
isn’t an answer choice.
26. D 
If you look at this integral, you should notice that it is similar to the integral:
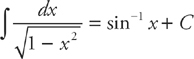
Step 1: If we factor 9 out of the radicand, we can convert our integral into the one above:
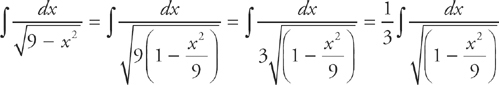
Step 2: Now we can use u-substitution. Let 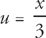 . Then du =
. Then du =  dx and 3 du = dx.
dx and 3 du = dx.
We get: 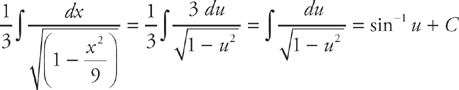
Step 3: Substituting back, we get:
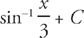
27. B Find 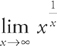
This is a limit of an indeterminate form. We use L’Hôpital’s Rule to evaluate these limits, but we need to get this into the form 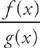 so that we can take the derivative of the top and bottom. We do this using logarithms.
so that we can take the derivative of the top and bottom. We do this using logarithms.
Step 1: First, let 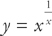
Step 2: Now, take the log of both sides (remember, when we say log, we mean natural log, not common log).
We get 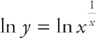 , which we can rewrite, using log rules, as
, which we can rewrite, using log rules, as 
Step 3: Now we can use L’Hôpital’s Rule. Take the derivative of the top and bottom.
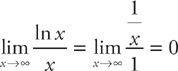
Be careful! This is NOT the answer! We just found that the limit of ln y → 0; therefore, y → e0 = 1. Whenever you use this technique, remember to reverse the logarithm at the end.
28. B What is the sum of the Maclaurin series 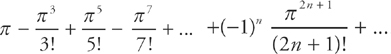 ?
?
This series is of the form  . This, as we know, is the Maclaurin series expansion of sin x. In the problem, we simply have π instead of x. Therefore, this is equal to sinπ = 0.
. This, as we know, is the Maclaurin series expansion of sin x. In the problem, we simply have π instead of x. Therefore, this is equal to sinπ = 0.
29. C The first three non-zero terms in the Taylor series about x = 0 for cos x are
This is a Taylor series problem. There are four Taylor series that you should memorize. This is one of them. But just in case you didn’t memorize it…
Step 1: The formula for a Taylor series about the point x = a is:

Step 2: First, let’s take the first few derivatives of cos x:
f(x) = cos x
f′(x) = –sin x
f″(x) = –cos x
f′″(x) = sin x
f(4)(x) = cos x
Step 3: Next, we evaluate each of these at a = 0:
f(0) = cos 0 = 1
f′(0) = –sin 0 = 0
f″(0) = –cos 0 = –1
f′″(0) = sin 0 = 0
f (4)(0) = cos 0 = 1
Step 4: Now if we plug in 0 for a throughout the formula we get:

You should make sure to memorize the four Taylor series in the unit. One of them almost always shows up on the AP examination!
30. C 
This is a trigonometric integral. Generally, these are solved by using the trigonometric substitutions that you learned in precalculus. If you are unfamiliar with these, you should go back and review them.
Step 1: First, rewrite cos3 x as cos x(cos2 x). Then, because cos2 x = (1 – sin2 x), we can rewrite the integral as:

Step 2: The first integral is easy: 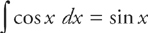 . We do the second integral with u-substitution.
. We do the second integral with u-substitution.
Let u = sin x and du = cos x dx. Then 
Substituting back for u and combining gives us:
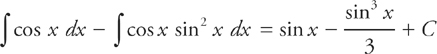
31. A If f(x) = (3x)(3x) then f′(x) =
This problem requires us to find the derivative of an exponential function. Any power of x can be written as a power of e, which is what we will use to do this derivative.
Step 1: Rewrite (3x)(3x) = e(3x)ln(3x). Now, we can take the derivative of this using the Chain Rule and the Product Rule.
Step 2: 
Step 3: Now, replacing e(3x)ln(3x) with (3x)(3x), gives us (3x)(3x)(3 + 3ln(3x)).
32. C To what limit does the sequence  converge as n approaches infinity?
converge as n approaches infinity?
This will require us to use one of the convergence tests for Infinite series. If we use the ratio test, we will be able to tell if the sequence converges, and, if so, to what value.
Step 1: 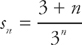 and
and 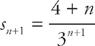 . So the ratio test says that, if
. So the ratio test says that, if  , then the sequence will converge to zero, and if
, then the sequence will converge to zero, and if 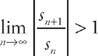 , then the series diverges—in other words, it has no limit.
, then the series diverges—in other words, it has no limit.
Step 2: 
If we take the limit,  .
.
Because this is less than one, the sequence converges to zero.
33. B 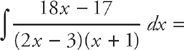
This is another partial fractions integral.
Step 1: Write the integrand as: 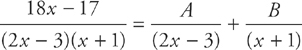
Step 2: Multiply both sides by: (2x – 3)(x + 1)
Step 3: Now we have: 18x – 17 = A(x + 1) + B(2x – 3)
Step 4: 18x – 17 = Ax + A + 2Bx – 3B
Step 5: 18x – 17 = (Ax + 2Bx) + (A – 3B)
Step 6: 18x – 17 = x(A + 2B) + (A – 3B)
Step 7: Thus: (A + 2B) = 18 and (A – 3B) = –17
Step 8: Solve this using simultaneous equations to get: A = 4 and B = 7
Step 9: We can now rewrite the original integral as:
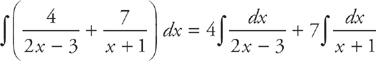
Step 10: These are both basic ln integrals, and we get:
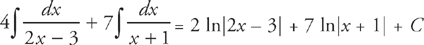
34. B A particle moves along a path described by x = cos3 t and y = sin3 t. Find the distance that the particle travels along the path from t = 0 to t =  .
.
This is another arc length problem.
Step 1: The formula for the arc length of a curve given in parametric form on the interval [a, b] is: 
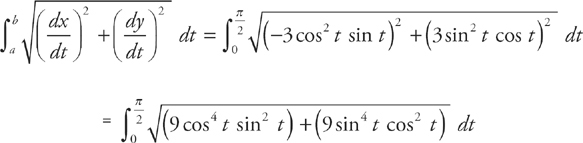
Step 3: Now you have a choice. You can integrate this using your calculator. You should get 1.5.
If you are not comfortable with this on the calculator, or if you prefer to do the integration, you need to do the following. Reduce the integrand by factoring out sin2 t cos2 t and we get:

Step 4: Using u-substitution, let u = sin t and du = cos t. Then we get:

35. E The sales price of an item is 800 – 35x dollars and the total manufacturing cost is 2x3 – 140x2 + 2,600x + 10,000 dollars, where x is the number of items. What number of items should be manufactured in order to optimize the manufacturer’s total profit?
Anytime that you see the word “optimize,” you will be doing a maximum/minimum problem. The profit is the number of items sold times the difference between the sales price of each object and its cost. The number of items is x, so the total sales price is 800x – 35x2.
Step 1: Let P equal profit:
P = 800x – 35x2 – (2x3 – 140x2 + 2,600x + 10,000) = –2x3 + 105x2 – 1,800x – 10,000
Step 2:  = –6x2 + 210x – 1,800. Setting it equal to 0 we get:
= –6x2 + 210x – 1,800. Setting it equal to 0 we get:
–6x2 + 210x – 1,800 = 0
x2 – 35x + 300 = 0
(x – 20)(x – 15) = 0
x = 15, 20
Step 3: In order to determine which of these is the maximum and which is the minimum, use the second derivative test. The second derivative of profit is 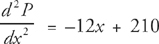 . At x = 15, we get
. At x = 15, we get 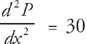 , so this is a minimum. At x = 20, we get
, so this is a minimum. At x = 20, we get  , so this is a maximum. Therefore, the optimum number of units is 20.
, so this is a maximum. Therefore, the optimum number of units is 20.
36. D Find the area enclosed by the polar equation r = 4 + cos θ for 0 ≤ θ ≤ 2π.
Step 1: This problem requires you to know the polar formula for finding the area of a region. The formula is  .
.
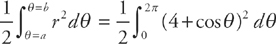 . Use your calculator to get 51.8363.
. Use your calculator to get 51.8363.
If you don’t want to do this integral with the calculator, do the following:
If we expand the integrand, we will get three integrals:
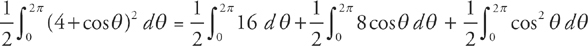
The first two integrals are easy and give us:
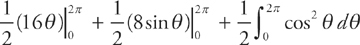
Evaluating the first two integrals, we get  .
.
Step 2: We do the third integral using a trigonometric substitution:

If we simplify this integral, we get:
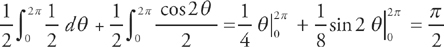
If we add 16π +  , we get
, we get 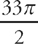 .
.
37. D Use the Trapezoid Rule with n = 4 to approximate the area between the curve f(x) = x3 – x2 and the x-axis from x = 3 to x = 4.
This problem will require you to be familiar with the Trapezoid Rule. This is very easy to do on the calculator, and some of you may even have written programs to evaluate this. Even if you haven’t, the formula is easy. The area under a curve from x = a to x = b, divided into n intervals is approximated by the Trapezoid Rule and is:
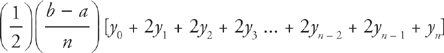
This formula may look scary, but it actually is quite simple, and the AP examination never uses a very large value for n anyway.
Step 1: 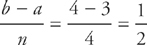
Plugging into the formula, we get:
 [(33 – 32) + 2(3.253 – 3.252) + 2(3.53 – 3.52) + 2(3.753 – 3.752) + (43 – 42)]
[(33 – 32) + 2(3.253 – 3.252) + 2(3.53 – 3.52) + 2(3.753 – 3.752) + (43 – 42)]
This is easy to plug into your calculator and you will get 31.516.
38. E If 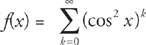 , then
, then 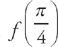 is
is
Step 1: If a series is of the form 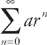 and |r| < 1, then the sum of the series is
and |r| < 1, then the sum of the series is 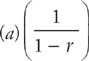 , where a is the first term. (Notice that if the series went from one to infinity, instead of zero to infinity, then the formula would be
, where a is the first term. (Notice that if the series went from one to infinity, instead of zero to infinity, then the formula would be 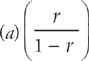 . Be careful that you memorize the correct formula. You could avoid this confusion by deriving the formula as you do the problem. To learn how to do that, refer to the unit on Infinite Series.) Here r is cos2 x and a is 1, and |cos2 x| < 1. This is very important. If |r| ≥ 1, the formula doesn’t work. So the sum is (1)
. Be careful that you memorize the correct formula. You could avoid this confusion by deriving the formula as you do the problem. To learn how to do that, refer to the unit on Infinite Series.) Here r is cos2 x and a is 1, and |cos2 x| < 1. This is very important. If |r| ≥ 1, the formula doesn’t work. So the sum is (1)  .
.
Using trigonometric substitution, this sum can be simplified to:  .
.
Now if we plug in 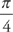 for x, we get:
for x, we get: 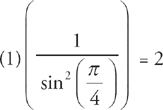 .
.
39. B The volume of the solid that results when the area between the graph of y = x2 + 2 and the graph of y = 10 – x2 from x = 0 to x = 2 is rotated around the x-axis is:
This is another volume of a solid of revolution problem. As you should have noticed by now, these are very popular on the AP Examination and show up in both the multiple choice section and in the free-response section. If you are not good at these, go back and review the unit carefully. You cannot afford to get these wrong on the AP exam! The good thing about this volume problem is that it is in the calculator part of the multiple-choice section, so you can use a program and your graphing calculator to assist you with this problem.
Step 1: First, graph the two curves on the same set of axes. The graph should look like this:

Step 2: Now look at the answer choices. Notice that each answer choice is the sum of two integrals, and all of the functions are in terms of y. This means that you are going to have to use the method of shells, and that you will have to convert the functions from being in terms of x to being in terms of y. Also, when you make a horizontal slice in this region, you are using different curves above and below the intersection point, so you will have to do two integrals. Okay. One thing at a time.
Step 3: First let’s find where the two curves intersect. We can do this either with the calculator or algebraically.
Algebraically, we set the two equations equal to each other:
x2 + 2 = 10 – x2
2x2 = 8
x2 = 4
x = ± 2
We will use x = 2, and plugging in 2 for x, we get y = 6.
Now we have to find what y is when x = 0. On the lower curve, y = 2. On the higher curve, y = 10. These then are our limits of integration. We will have two integrals, one from 2 to 6, the other from 6 to 10. By process of elimination, this means that the answer can be only (B) or (C).
Step 4: Now we have to convert each of the equations to being in terms of y:
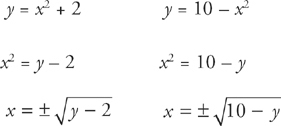
Step 5: We are concerned with only the positive roots for this region, so using the Shells formula, we get that the volume is  .
.
40. A 
Remember that this is the calculator part of the test. You can simply evaluate this on your calculator using fnint. If you are not comfortable with this, we will show you how to do this algebraically. This integral requires a trigonometric substitution. These types of integrals require a lot of algebra, so you should leave them for the second pass.
Step 1: Using your calculator, enter fnint  . You should get 1.0986. Evaluate each of the answer choices to see which has the same value, or which is closest.
. You should get 1.0986. Evaluate each of the answer choices to see which has the same value, or which is closest.
Step 2: If you are not using your calculator, you first have to do a substitution. Let’s ignore the limits of integration for now, and just evaluate the integral. Whenever we have an integral of the form 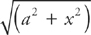 , we do the substitution x = a tan θ. So here we let x = 3 tan θ and dx = 3 sec2 θ dθ.
, we do the substitution x = a tan θ. So here we let x = 3 tan θ and dx = 3 sec2 θ dθ.
Substituting into the integrand, we get: 
If we factor 9 out of the radical in the denominator, we get :

You should have memorized this integral. It is ln|sec θ + tan θ|.
Step 3: Now we want to evaluate the limits of integration, but in order to do that,
we should substitute back for x. If x = 3 tan θ, then 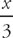 = tan θ. Using the Pythagorean theorem,
= tan θ. Using the Pythagorean theorem, 
So now we have  . If we evaluate the limits of integration, we get:
. If we evaluate the limits of integration, we get:
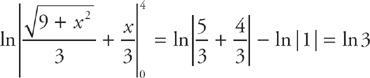
41. D The rate that an object cools is directly proportional to the difference between its temperature (in Kelvin) at that time and the surrounding temperature (in Kelvin). If an object is initially at 35K, and the surrounding temperature remains constant at 10K, it takes 5 minutes for the object to cool to 25K. How long will it take for the object to cool to 20K?
This is a differential equation. Each AP examination tends to contain one differential equation word problem. They usually give you the same type of equation and are actually not terribly difficult, once you understand the question.
Step 1: The first sentence tells us what the equation is going to be. Let T stand for temperature at a particular time, and S stand for the surrounding temperature. Then our equation is:  = k(T – S). Time is always represented by t, and k is a constant.
= k(T – S). Time is always represented by t, and k is a constant.
This equation is solvable using separation of variables. Put everything that contains a T on the left side, and everything that contains a t on the right side:
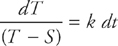
If we integrate both sides we get: 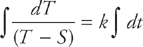
And performing the integration gives us: ln|T – S| = kt + C.
Step 2: Whenever we have an equation of this form, we then exponentiate both sides, giving us:
|T – S| = ekt + C or |T – S| = Cekt
If we plug in the rest of the information from the problem, we can solve for the constants k and C.
The initial temperature tells us that at time t = 0, T = 35, and S = 10.
So |35 – 10| = Cek(0) and 25 = C
Then at time t = 5, T = 25. So:

This gives us the final equation 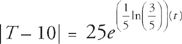 .
.
Step 3: Finally, we plug in the last bit of information, that T = 20 to solve for t.

42. A 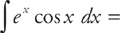
You should recognize this integral as an elementary integration by parts integral. If so, this won’t be very hard to do.
Step 1: Let u = ex and dv = cos x dx
du = ex dx v = sin x
Step 2: We need to do integration by parts a second time to evaluate the second integral:
Let u = ex and dv = sin x dx
du = ex dx v = –cos x
Now we have: 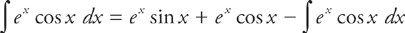
Step 3: Although this looks as if we are back where we started, and will have to do a third integration, if we add  to both sides we get:
to both sides we get:

Now if we divide both sides by 2 we get:

43. D Two particles leave the origin at the same time and move along the y-axis with their respective positions determined by the functions y1 = cos 2t and y2 = 4 sin t for 0 < t < 6. For how many values of t do the particles have the same acceleration?
If you want to find acceleration, all you have to do is take the second derivative of the position functions.
Step 1: 
Step 2: Now all we have to do is to graph both of these equations on the same set of axes on a calculator. You should make the window from x = 0 to x = 7 (leave yourself a little room so that you can see the whole range that you need). You should get a picture that looks like this:
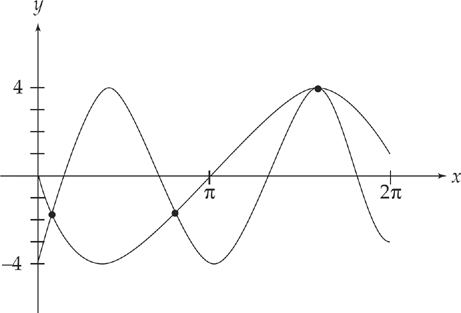
Where the graphs intersect, the acceleration is the same. There are three points of intersection.
44. E The minimum value of the function y = x3 – 7x + 11, x ≥ 0, is approximately
You have two options. First, let’s do the problem without using the calculator.
If we want to find the minimum, we take the derivative and set it equal to zero. We get:  = 3x2 – 7 = 0. Now we solve for x:
= 3x2 – 7 = 0. Now we solve for x:

We are concerned with only positive values of x (note the restriction in the problem), so let’s look at  . First, we have to determine whether this is a minimum or a maximum. The simplest way to do this is with the second derivative test. Take the second derivative and we get:
. First, we have to determine whether this is a minimum or a maximum. The simplest way to do this is with the second derivative test. Take the second derivative and we get: 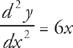 . Now, plug in
. Now, plug in 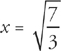 . The second derivative is positive there, so the point is a minimum.
. The second derivative is positive there, so the point is a minimum.
Now, we plug 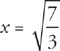 back into the original equation to find the y value.
back into the original equation to find the y value.
 (rounded to 3 decimal places).
(rounded to 3 decimal places).
Now let’s do this using the calculator.
Using the TI 82/83, press Y= and enter the graph as Y1 = x^3 – 7x + 11.
45. C Use Euler’s Method with h = 0.2 to estimate y(1), if y′ = y and y(0) = 1.
We are given that the curve goes through the point (0,1). We will call the coordinates of this point x0 = 0 and y0 = 1. The slope is found by plugging y0 = 1 into y′ = y, so we have an initial slope of y′0 = 1.
Now we need to find the next set of points.
Step 1: Increase x0 by h to get x1:
x1 = 0.2
Step 2: Multiply h by y′0 and add to y0 to get y1:
y1 = 1 + 0.2(1) = 1.2
Step 3: Find y′1 by plugging y1 into the equation for y′ :
y′1= 1.2
Repeat until you get to x = 1.
Step 1: Increase x1 by h to get x2:
x2 = 0.4
Step 2: Multiply h by y′1 and add to y1 to get y2:
y2 = 1.2 + 0.2(1.2) = 1.44
Step 3: Find y′2 by plugging y2 into the equation for y′ :
y′2 = 1.44
Step 1: x3 = x2 + h:
x3 = 0.6
y3 = 1.44 + 0.2(1.44) = 1.728
Step 3: y′3 = y3:
y′3 = 1.728
Step 1: x4 = x3 + h:
x4 = 0.8
Step 2: y4 = y3 + h(y′3):
y4 = 1.728 + 0.2(1.728) = 2.0736
Step 3: y′4 = y4:
y′4 = 2.0736
Step 1: x5 = x4 + h:
x5 = 1.0
Step 2: y5 = y4 + h(y′4):
y5 = 2.0736 + 0.2(2.0736) = 2.48832
We don’t need to go any farther because we are asked for the value of y when x = 1.
The answer is y = 2.48832.
 and
and  , so:
, so: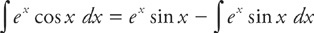

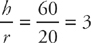 (remember that the radius is half the diameter). If we solve this for h and substitute, we get:
(remember that the radius is half the diameter). If we solve this for h and substitute, we get:
 .
.
 .
. ft/sec.
ft/sec.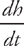 . In order to do this, we need to go back to our ratio of height to radius and solve it for the radius:
. In order to do this, we need to go back to our ratio of height to radius and solve it for the radius: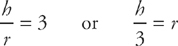
 .
.

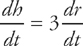 in part (b), we merely had to multiply it by 3 to find the answer for part (c).
in part (b), we merely had to multiply it by 3 to find the answer for part (c). , where the starting time is a, and the ending time is b.
, where the starting time is a, and the ending time is b.

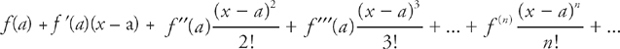
 , so you don’t have to do all of the work here. You can just substitute –4x2 for u:
, so you don’t have to do all of the work here. You can just substitute –4x2 for u: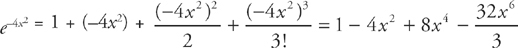
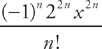

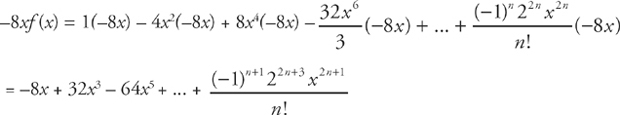

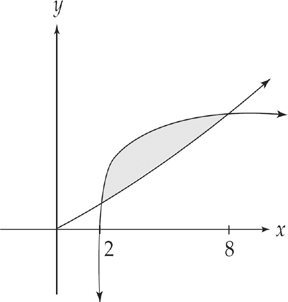
 , and the lines x = 2 and x = 8.
, and the lines x = 2 and x = 8.
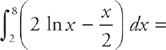 .
.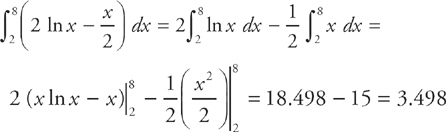
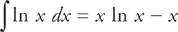 or you can do it as one of the basic integration-by-parts integrals.
or you can do it as one of the basic integration-by-parts integrals.
 .
.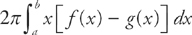
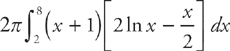


 .
. , then the limit of the derivatives of the numerator is the same as the limit of the original quotient. In other words, if we differentiate the top and bottom of the quotient, we will get the limit. First, we have to show that the quotient gives us an indeterminate form:
, then the limit of the derivatives of the numerator is the same as the limit of the original quotient. In other words, if we differentiate the top and bottom of the quotient, we will get the limit. First, we have to show that the quotient gives us an indeterminate form:
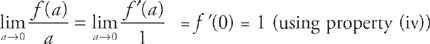
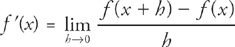
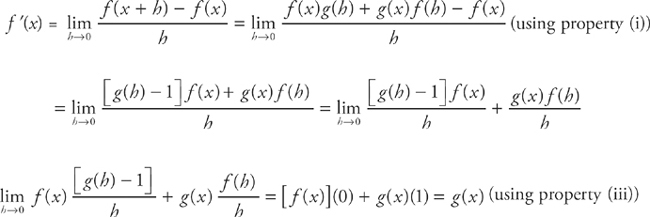
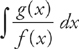 .
.