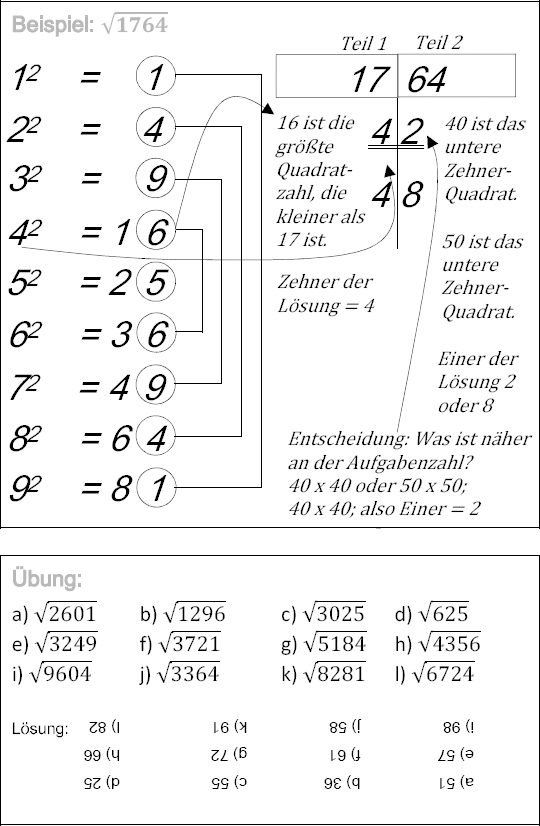
Was? Wurzel ziehen

Aufgehende Quadratwurzel

Wozu?

Aufgehende Wurzeln ziehen im Zahlenraum von 100 bis 10 000.

Wie?

1. Die Aufgabenzahl wird in zwei Teile zerlegt: Teil 1 (Tausender und Hunderter) und Teil 2 (Zehner und Einer). Z.B. 1296 in 12 und 96 oder 2304 in 23 und 04. Wenn die Aufgabenzahl 3-stellig ist, in Teil 1 (Hunderter) und Teil 2 (Zehner und Einer). Also z.B.: 121 in 1 und 21 oder 256 in 2 und 56.
2. Die Lösungen sind immer zweistellig. Also von 10 bis 99. Ausnahme 100² = 10000.
3. Den Zehner der Lösung ermittelt man durch Finden der größten Quadratzahl, die kleiner oder gleich des ersten Teils ist. Z.B.: Teil 1 = 12, dann ist es eben die 9 (32). 16 (42) wäre ja schon größer als 12. Also ist 3² der Zehner der Lösung.
4. Den Einer der Lösung ermittelt man durch Prüfen der Einerstelle der Aufgabenzahl. Z.B. bei der Aufgabenzahl 1296 ist das die 6. Nun vergleicht man die 6 mit allen Quadratzahlen von einstelligen Zahlen (1, 4, 9, 16, 25, 36, 49, 64, 81) und welche von diesen auch auf 6 endet. Es sind die Zahlen 16 (42) und 36 (62). Man hat jetzt zwei Alternativen für die Einerstelle der Lösung: 4 und 6. Also heißt die komplette Lösung der Aufgabe entweder 34 oder 36.
5. Entscheidung: Man bildet das untere Zehnerquadrat 40 x 40 (1600) und das obere Zehnerquadrat 50 x 50 (1600) und vergleicht mit der Aufgabenzahl 1296. Was ist näher an der Aufgabenzahl dran? 1600 ist näher an 1296 dran. Daher 4.