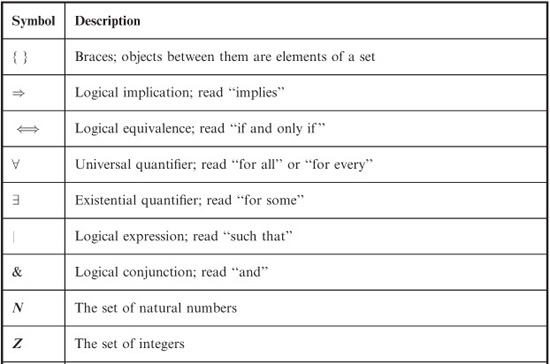
Mathematics is expressed in language alien to people unfamiliar with it. Someone talking about mathematics can sound like a rocket scientist. Written mathematical documents are often laden with symbology. Before you proceed further, look over Table 1-1. It will help you remember symbols used in basic mathematics, and might introduce you to a few symbols you’ve never seen before!
If at first some of this stuff seems theoretical and far-removed from “the everyday world,” think of it as basic training, a sort of math boot camp. Or better yet, think of it as the classroom part of drivers’ education. It was good to have that training so you’d know how to read the instrument panel, find the turn signal lever, adjust the mirrors, control the headlights, and read the road signs. So get ready for a drill. Get ready to think logically. Get your mind into math mode.
Table 1-1 Symbols used in basic mathematics.

A set is a collection or group of definable elements or members. Set elements commonly include:
• points on a line
• instants in time
• coordinates in a plane
• coordinates in space
• coordinates on a display
• curves on a graph or display
• physical objects
• chemical elements
• locations in memory or storage
• data bits, bytes, or characters
• subscribers to a network
If an object or number (call it a) is an element of set A, this fact is written as:
a ∈ A
The ∈ symbol means “is an element of.”
The intersection of two sets A and B, written A ∩ B, is the set C such that the following statement is true for every element x:
x ∈ C if and only if x ∈ A and x ∈ B
The ∩ symbol is read “intersect.”
The union of two sets A and B, written A ∪ B, is the set C such that the following statement is true for every element x:
x ∈ C if and only if x ∈ A or x ∈ B
The ∪ symbol is read “union.”
A set A is a subset of a set B, written A ⊆ B, if and only if the following holds true:
x ∈ A implies that x ∈ B
The ⊆ symbol is read “is a subset of.” In this context, “implies that” is meant in the strongest possible sense. The statement “This implies that” is equivalent to “If this is true, then that is always true.”
A set A is a proper subset of a set B, written A ⊂ B, if and only if the following both hold true:
x ∈ A implies that x ∈ B
as long as A ≠ B
The ⊂ symbol is read “is a proper subset of.”
Two sets A and B are disjoint if and only if all three of the following conditions are met:
A ≠ Ø
B ≠ Ø
A ∩ B = Ø
where Ø denotes the empty set, also called the null set. It is a set that doesn’t contain any elements, like a basket of apples without the apples.
Two non-empty sets A and B are coincident if and only if, for all elements x, both of the following are true:
x ∈ A implies that x ∈ B
x ∈ B implies that x ∈ A
A number is an abstract expression of a quantity. Mathematicians define numbers in terms of sets containing sets. All the known numbers can be built up from a starting point of zero. Numerals are the written symbols that are agreed-on to represent numbers.
The natural numbers, also called whole numbers or counting numbers, are built up from a starting point of 0 or 1, depending on which text you consult. The set of natural numbers is denoted N. If we include 0, we have this:
N = {0, 1, 2, 3,. . ., n,. . .}
In some instances, 0 is not included, so:
N = {1, 2, 3, 4,. . ., n,. . .}
Natural numbers can be expressed as points along a geometric ray or half-line, where quantity is directly proportional to displacement (Fig. 1-1).
The decimal number system is also called base 10 or radix 10. Digits in this system are the elements of the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Numerals are written out as strings of digits to the left and/or right of a radix point, which is sometimes called a “decimal point.”
In the expression of a decimal number, the digit immediately to the left of the radix point is multiplied by 1, and is called the ones digit. The next digit to the left is multiplied by 10, and is called the tens digit. To the left of this are digits representing hundreds, thousands, tens of thousands, and so on.
The first digit to the right of the radix point is multiplied by a factor of 1/10, and is called the tenths digit. The next digit to the right is multiplied by 1/100, and is called the hundredths digit. Then come digits representing thousandths, ten-thousandths, and so on.

Fig. 1-1. The natural numbers can be depicted as points on a half-line or ray.
The binary number system is a scheme for expressing numbers using only the digits 0 and 1. It is sometimes called base 2. The digit immediately to the left of the radix point is the “ones” digit. The next digit to the left is the “twos” digit; after that comes the “fours” digit. Moving further to the left, the digits represent 8, 16, 32, 64, and so on, doubling every time. To the right of the radix point, the value of each digit is cut in half again and again, that is, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, and so on.
When you work with a computer or calculator, you give it a decimal number that is converted into binary form. The computer or calculator does its operations with zeros and ones, also called digital low and high states. When the process is complete, the machine converts the result back into decimal form for display.
The octal number system uses eight symbols. Every digit is an element of the set {0, 1, 2, 3, 4, 5, 6, 7}. Starting with 1, counting in the octal system goes like this: 1, 2, 3, 4, 5, 6, 7, 10, 11, 12,. . . 16, 17, 20, 21,. . . 76, 77, 100, 101,. . . 776, 777, 1000, 1001, and so on.
Yet another scheme, commonly used in computer practice, is the hexadecimal number system, so named because it has 16 symbols. These digits are the decimal 0 through 9 plus six more, represented by A through F, the first six letters of the alphabet. Starting with 1, counting in the hexadecimal system goes like this: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11,. . . 1E, 1F, 20, 21,. . . FE, FF, 100, 101,. . . FFE, FFF, 1000, 1001, and so on.
What is the value of the binary number 1001011 in the decimal system?
Note the decimal values of the digits in each position, proceeding from right to left, and add them all up as a running sum. The right-most digit, 1, is multiplied by 1. The next digit to the left, 1, is multiplied by 2, for a running sum of 3. The digit to the left of that, 0, is multiplied by 4, so the running sum is still 3. The next digit to the left, 1, is multiplied by 8, so the running sum is 11. The next two digits to the left of that, both 0, are multiplied by 16 and 32, respectively, so the running sum is still 11. The left-most digit, 1, is multiplied by 64, for a final sum of 75. Therefore, the decimal equivalent of 1001011 is 75.
What is the value of the binary number 1001.011 in the decimal system?
To solve this problem, begin at the radix point. Proceeding to the left first, figure out the whole-number part of the expression. The right-most digit, 1, is multiplied by 1. The next two digits to the left, both 0, are multiplied by 2 and 4, respectively, so the running sum is still 1. The left-most digit, 1, is multiplied by 8, so the final sum for the whole-number part of the expression is 9.
Return to the radix point and proceed to the right. The first digit, 0, is multiplied by 1/2, so the running sum is 0. The next digit to the right, 1, is multiplied by 1/4, so the running sum is 1/4. The right-most digit, 1, is multiplied by 1/8, so the final sum for the fractional part of the expression is 3/8.
Adding the fractional value to the whole-number value in decimal form produces the decimal equivalent of 1001.011, which is 9-3/8.
The set of natural numbers can be duplicated and inverted to form an identical, mirror-image set:
– N = {0, – 1, – 2, – 3,. . .}
The union of this set with the set of natural numbers produces the set of integers, commonly denoted Z:
Z = N ∪ –N
= {. . ., – 3, – 2, – 1, 0, 1, 2, 3,. . .}
Integers can be expressed as points along a line, where quantity is directly proportional to displacement (Fig. 1-2). In the illustration, integers correspond to points where hash marks cross the line. The set of natural numbers is a proper subset of the set of integers:

Fig. 1-2. The integers can be depicted as points on a line.
N ⊂ Z
For any number a, if a ∈ N, then a ∈ Z. This is formally written:
∀a: a ∈ N ⇒ a ∈ Z
The converse of this is not true. There are elements of Z (namely, the negative integers) that are not elements of N.
Addition is symbolized by the plus sign (+). The result of this operation is a sum. Subtraction is symbolized by a long dash (–). The result of this operation is a difference. In a sense, these operations “undo” each other. For any integer a, the addition of an integer –a to a quantity is equivalent to the subtraction of the integer a from that quantity. The subtraction of an integer –a from a quantity is equivalent to the addition of the integer a to that quantity.
Multiplication is symbolized by a tilted cross (×), a small dot (·), or sometimes in the case of variables, by listing the numbers one after the other (for example, ab). Occasionally an asterisk (*) is used. The result of this operation is a product.
On the number line of Fig. 1-2, products are depicted by moving away from the zero point, or origin, either toward the left or toward the right depending on the signs of the numbers involved. To illustrate a × b = c, start at the origin, then move away from the origin a units b times. If a and b are both positive or both negative, move toward the right; if a and b have opposite sign, move toward the left. The finishing point corresponds to c.
The preceding three operations are closed over the set of integers. This means that if a and b are integers, then a + b, a – b, and a × b are integers. If you add, subtract, and multiply integers by integers, you can never get anything but another integer.
Division is symbolized by a forward slash (/) or a dash with dots above and below (÷). The result of this operation is called a quotient. When a quotient is expressed as a ratio or as a proportion, a colon is often used between the numbers involved.
On the number line of Fig. 1-2, quotients are depicted by moving in toward the origin, either toward the left or toward the right depending on the signs of the numbers involved. To illustrate a/b = c, it is easiest to envision the product b × c = a performed “backwards.” (Or you can simply use a calculator!)
The operation of division, unlike the operations of addition, subtraction, and multiplication, is not closed over the set of integers. If a and b are integers, then a/b might be an integer, but this is not necessarily the case. Division gives rise to a more comprehensive set of numbers, which we’ll look at shortly. The quotient a/b is not defined at all if b = 0.
Exponentiation, also called raising to a power, is symbolized by a superscript numeral. The result of this operation is known as a power.
If a is an integer and b is a positive integer, then ab is the result of multiplying a by itself b times. For example:
23 = 2 × 2 × 2 = 8
34 = 3 × 3 × 3 × 3 = 81
If a is an integer and c is a negative integer, then ac is the result of multiplying a by itself c times and then dividing 1 by the result. For example,
2–3 = 1/(2 × 2 × 2) = 1/8
3–4 = 1/(3 × 3 × 3 × 3) = 1/81
Let p be a nonzero natural number. Suppose ab = p, where a and b are natural numbers. Further suppose that either of the following statements is true for all a and b:
(a = 1) & (b = p)
(a = p) & (b = 1)
Then p is defined as a prime number. In other words, a natural number p is prime if and only if its only two natural-number factors are 1 and itself.
The first several prime numbers are 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and 37. Sometimes 1 is not included in this list, although technically it meets the above requirement for “prime-ness.”
Suppose n is a natural number. Then there exists a unique sequence of prime numbers p1, p2, p3,. . ., pm, such that both of the following statements are true:
p1 ≤ p2 ≤ p3 ≤. . . ≤ pm
p1 × p2 × p3 ×. . . × pm = n
The numbers p1, p2, p3,. . ., pm are called the prime factors of the natural number n. Every natural number n has one, but only one, set of prime factors. This is an important principle known as the Fundamental Theorem of Arithmetic.
What are the prime factors of 80?
Here’s a useful hint for finding the prime factors of any natural number n: Unless n is a prime number, all of its prime factors are less than or equal to n/2. In this case n = 80, so we can be certain that all the prime factors of 80 are less than or equal to 40.
Finding the prime factors is largely a matter of repeating this divide-by-2 process over and over, and making educated guesses to break down the resulting numbers into prime factors. We can see that 80 = 2 × 40. Breaking it down further:
80 = 2 × (2 × 20)
= 2 × 2 × (2 × 10)
= 2 × 2 × 2 × 2 × 5
Is the number 123 prime? If not, what are its prime factors?
The number 123 is not prime. It can be factored into 123 = 41 × 3. The numbers 41 and 3 are both prime, so they are the prime factors of 123.
The natural numbers, or counting numbers, have plenty of interesting properties. But when we start dividing them by one another or performing fancy operations on them like square roots, trigonometric functions, and logarithms, things can get downright fascinating.
A rational number (the term derives from the word ratio) is a quotient of two integers, where the denominator is not zero. The standard form for a rational number a is:
a = m/n
where m and n are integers, and n ≠ 0. The set of all possible such quotients encompasses the entire set of rational numbers, denoted Q. Thus,
Q = {r | r = m/n}
where m ∈ Z, n ∈ Z, and n ≠ 0. The set of integers is a proper subset of the set of rational numbers. Thus, the natural numbers, the integers, and the rational numbers have the following relationship:
N ⊂ Z ⊂ Q
Rational numbers can be denoted in decimal form as an integer, followed by a radix point, followed by a sequence of digits. (See Decimal numbers above for more details concerning this notation.) The digits following the radix point always exist in either of two forms:
• a finite string of digits
• an infinite string of digits that repeat in cycles
Examples of the first type of rational number, known as terminating decimals, are:
3/4 = 0.750000. . .
–9/8 = –1.1250000. . .
Examples of the second type of rational number, known as nonterminating, repeating decimals, are:
1/3 = 0.33333. . .
–1/6 = –0.166666. . .
One of the most interesting things about rational numbers is the fact that they are “dense.” Suppose we assign rational numbers to points on a line, in such a way that the distance of any point from the origin is directly proportional to its numerical value. If a point is on the left-hand side of the point representing 0, then that point corresponds to a negative number; if it’s on the right-hand side, it corresponds to a positive number. If we mark off only the integers on such a line, we get a picture that looks like Fig. 1-2. But in the case of the rational numbers, there are points all along the line, not only at those places where the hash marks cross the line.
If we take any two points a and b on the line that correspond to rational numbers, then the point midway between them corresponds to the rational number (a + b)/2. This is true no matter how many times we repeat the operation. We can keep cutting an interval in half forever, and if the end points are both rational numbers, then the midpoint is another rational number. Figure 1-3 shows an example of this. It is as if you could take a piece of paper and keep folding it over and over, and never get to the place where you couldn’t fold it again.
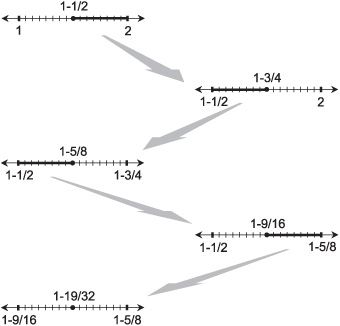
Fig. 1-3. An interval can be repeatedly cut in half, generating rational numbers without end.
It is tempting to suppose that points on a line, defined as corresponding to rational numbers, are “infinitely dense.” They are, in a sense, squeezed together “infinitely tight” so that every point in between any two points must correspond to some rational number. But do the rational numbers account for all of the points along a true geometric line? The answer, which surprises many folks the first time they hear it, is “No.”
An irrational number is a number that cannot be expressed as the ratio of two integers. Examples of irrational numbers include:
• the length of the diagonal of a square that is one unit on each edge
• the circumference-to-diameter ratio of a circle.
All irrational numbers share the property of being inexpressible in decimal form. When an attempt is made to express such a number in this form, the result is a nonterminating, nonrepeating decimal. No matter how many digits are specified to the right of the radix point, the expression is only an approximation of the actual value of the number. The set of irrational numbers can be denoted S. This set is entirely disjoint from the set of rational numbers. That means that no irrational number is rational, and no rational number is irrational:
S ∩ Q = Ø
The set of real numbers, denoted R, is the union of the sets of rational and irrational numbers:
R = Q ∪ S
For practical purposes, R can be depicted as the set of points on a continuous geometric line, as shown in Fig. 1-2. (In theoretical mathematics, the assertion that the points on a geometric line correspond one-to-one with the real numbers is known as the Continuum Hypothesis.) The real numbers are related to the rational numbers, the integers, and the natural numbers as follows:
N ⊂ Z ⊂ Q ⊂ R
The operations of addition, subtraction, multiplication, and division can be defined over the set of real numbers. If # represents any one of these operations and x and y are elements of R with y ≠ 0, then:
x # y ∈ R
Do you sense something strange going on here? We’ve just seen that the rational numbers, when depicted as points along a line, are “dense.” No matter how close together two rational-number points on a line might be, there is always another rational-number point between them. But this doesn’t mean that the rational-number points are the only points on a line.
Every rational number corresponds to some point on a number line such as the one shown in Fig. 1-2. But the converse of this statement is not true. There are some points on the line that don’t correspond to rational numbers. A good example is the positive number that, when multiplied by itself, produces the number 2. This is approximately equal to 1.41421. Another example is the ratio of the circumference of a circle to its diameter, a constant commonly called pi and symbolized π. It’s approximately equal to 3.14159.
The set of real numbers is more “dense” than the set of rational numbers. How many times more dense? Twice? A dozen times? A hundred times? It turns out that the set of real numbers, when depicted as the points on a line, is infinitely more dense than the set of real numbers. This is hard to imagine, and a proof of it is beyond the scope of this book. You might think of it this way: Even if you lived forever, you would die before you could name all the real numbers.
The symbol ℵ0 (aleph-null or aleph-nought) denotes the cardinality of the set of rational numbers. The cardinality of the real numbers is denoted ℵ1 (aleph-one). These “numbers” are called infinite cardinals or transfinite cardinals.
Around the year 1900, the German mathematician Georg Cantor proved that these two “numbers” are not the same. The infinity of the real numbers is somehow larger than the infinity of the rational numbers:
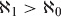
The elements of N can be paired off one-to-one with the elements of Z or Q, but not with the elements of S or R. Any attempt to pair off the elements of N and S or N and R results in some elements of S or R being left over without corresponding elements in N. This reflects the fact that the elements of N, Z, or Q can be defined in terms of a listing scheme (Fig. 1-4 is an example), but the elements of S or R cannot. It also reflects the fact that the points on a real-number line are more “dense” than the points on a line denoting the natural numbers, the integers, or the rational numbers.
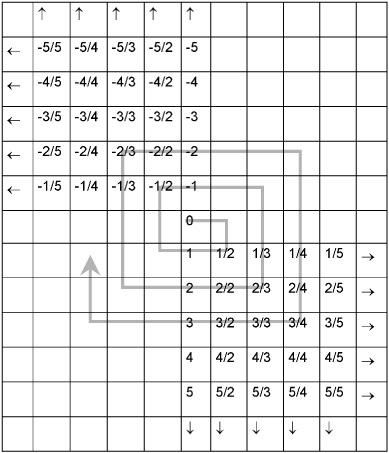
Fig. 1-4. A tabular listing scheme for the rational numbers. Proceed as shown by the gray line. If a box is empty, or if the number in it is equivalent to one encountered previously (such as 3/3 or –2/4), skip the box without counting it.
What is 4/7, expressed using only a radix point and decimal digits?
You can divide this out “longhand,” or you can use a calculator that has a display with a lot of digits. The result is:
4/7 = 0.571428571428571428. . .
That is zero, followed by a radix point, followed by the sequence of digits 571428 repeating over and over without end.
What is the value of 3.367367367 . . . expressed as a fraction?
First consider only the portion to the right of the radix point. This is a repeating sequence of the digits 367, over and over without end. Whenever you see a repeating sequence of several digits to the right of a radix point, its fractional equivalent is found by dividing that sequence of digits by an equal number of nines. In this case:
0.367367367. . . = 367/999
To get the value of 3.367367367 . . . as a fraction, simply add 3 to the above, getting:
3.367367367. . . = 3-367/999
In this context, the dash between the whole number portion and the fractional portion of the expression serves only to separate them for notational clarity. (It isn’t a minus sign!)
Several properties, also called principles or laws, are recognized as valid for the operations of addition, subtraction, multiplication, and division for all real numbers. Here are some of them. It’s not a bad idea to memorize these. You probably learned them in elementary school.
When 0 is added to any real number a, the sum is always equal to a. The number 0 is said to be the additive identity element:
a + 0 = a
When any real number a is multiplied by 1, the product is always equal to a. The number 1 is said to be the multiplicative identity element:
a × 1 = a
For every real number a, there exists a unique real number –a such that the sum of the two is equal to 0. The numbers a and –a are called additive inverses:
a + (–a) = 0
For every nonzero real number a, there exists a unique real number 1/a such that the product of the two is equal to 1. The numbers a and 1/a are called multiplicative inverses:
a × (1/a) = 1
The multiplicative inverse of a real number is also called its reciprocal.
When any two real numbers are added together, it does not matter in which order the sum is performed. The operation of addition is said to be commutative over the set of real numbers. For all real numbers a and b, the following equation is valid:
a + b = b + a
When any two real numbers are multiplied by each other, it does not matter in which order the product is performed. The operation of multiplication, like addition, is commutative over the set of real numbers. For all real numbers a and b, the following equation is always true:
a × b = b × a
A product can be written without the “times sign” (×) if, but only if, doing so does not result in an ambiguous or false statement. The above expression is often seen written this way:
ab = ba
If a = 3 and b = 52, however, it’s necessary to use the “times sign” and write this:
3 × 52 = 52 × 3
The reason becomes obvious if the above expression is written without using the “times signs.” This results in a false statement:
352 = 523
When adding any three real numbers, it does not matter how the addends are grouped. The operation of addition is associative over the set of real numbers. For all real numbers a1, a2, and a3, the following equation holds true:
(a1 + a2) + a3 = a1 + (a2 + a3)
When multiplying any three real numbers, it does not matter how the multiplicands are grouped. Multiplication, like addition, is associative over the set of real numbers. For all real numbers a, b, and c, the following equation holds:
(ab)c = a(bc)
For all real numbers a, b, and c, the following equation holds. The operation of multiplication is distributive with respect to addition:
a(b + c) = ab + ac
The above statement logically implies that multiplication is distributive with respect to subtraction, as well:
a(b – c) = ab – ac
The distributive law can also be extended to division as long as there aren’t any denominators that end up being equal to zero. For all real numbers a, b, and c, where a ≠ 0, the following equations are valid:
(ab + ac)/a = ab/a + ac/a = b + c
(ab – ac)/a = ab/a – ac/a = b – c
When addition, subtraction, multiplication, division, and exponentiation (raising to a power) appear in an expression and that expression must be simplified, the operations should be performed in the following sequence:
• Simplify all expressions within parentheses, brackets, and braces from the inside out.
• Perform all exponential operations, proceeding from left to right.
• Perform all products and quotients, proceeding from left to right.
• Perform all sums and differences, proceeding from left to right.
The following are examples of this process, in which the order of the numerals and operations is the same in each case, but the groupings differ:
[(2 + 3)(–3 – 1)2]2
= [5 × (–4)2]2
= (5 × 16)2
= 802 = 6400
[(2 + 3 × (–3) – 1)2]2
= [(2 + (–9) – 1)2]2
= (–82)2
= 642 = 4096
A note of caution is in order here: This rule doesn’t apply to exponents of exponents. For example, 33 raised to the power of 3 is equal to 273 or 19,683. But 3 raised to the power of 33 is equal to 327 or 7,625,597,484,987.
What is the value of the expression –5 × 6 + 8 – 1?
First, multiply –5 times 6, getting the product –30. Then add 8 to this, getting –22. Finally subtract 1, getting –23. Thus:
–5 × 6 + 8 – 1 = –23
What is the value of the expression –5 × (6 + 8 – 1)?
First find the sum 6 + 8, which is 14. Then subtract 1 from this, getting 13. Finally multiply 13 by –5, getting –65. Thus:
–5 × (6 + 8 – 1) = –65
The following rules and definitions apply to arithmetic operations for real numbers, with the constraint that no denominator can ever be equal to zero. It’s good to memorize these, because an “automatic” knowledge of them can save you some time as you hack your way through the occasional forest of calculations that life is bound to confront you with. After a while, these laws will seem like nothing more or less than common sense.
For all nonzero real numbers a, if 0 is divided by a, then the result is equal to 0. This equation is always true:
0/a = 0
For all real numbers a, if a is divided by 0, then the result a/0 is undefined. Perhaps a better way of saying this is that, whatever such an “animal” might happen to be, it is not a real number! Within the set of real numbers, there’s no such thing as the ratio of a number or variable to 0.
If you’re into playing around with numbers, you can have lots of fun trying to define “division by 0” and explore the behavior of ratios with zero denominators. If you plan to go on such a safari, however, take note: The “animals” can be unpredictable, and you had better fortify your mind with lots of ammunition and heavy armor.
Whenever a real number is multiplied by 0, the product is equal to 0. The following equations are true for all real numbers a:
a × 0 = 0
0 × a = 0
Whenever a nonzero real number is taken to the zeroth power, the result is equal to 1. The following equation is true for all real numbers a except 0:
a0 = 1
Suppose that a1, a2, a3,. . ., an be real numbers. The arithmetic mean, denoted mA (also known as the average) of a1, a2, a3,. . ., an is equal to the sum of the numbers, divided by the number of numbers. Mathematically:
mA = (a1 + a2 + a3 +. . . + an)/n
When two real numbers with plus signs (meaning positive, or larger than 0) or minus signs (meaning negative, or less than 0) are multiplied by each other, the following rules apply:
(+)(+) = (+)
(+)(–) = (–)
(–)(+) = (–)
(–)(–) = (+)
When two real numbers with plus or minus signs are divided by each other, the following rules apply:
(+)/(+) = (+)
(+)/(–) = (–)
(–)/(+) = (–)
(–)/(–) = (+)
When a real number with a plus sign or a minus sign is raised to a positive integer power n, the following rules apply:
(+)n = (+)
(–)n = (–) if n is odd
(–)n = (+) if n is even
For all nonzero real numbers, the reciprocal of the reciprocal is equal to the original number. The following equation holds for all real numbers a provided that a ≠ 0:
1/(1/a) = a
For all real numbers a, b, c, and d, the product of (a+ b) with (c + d) is given by the following formula:
(a + b)(c + d) = ac + ad + bc + bd
Given two quotients or ratios expressed as fractions, the numerator of the first times the denominator of the second is equal to the denominator of the first times the numerator of the second. Mathematically, for all real numbers a, b, c, and d where neither a nor b is equal to 0, the following statement is valid:
a/b = c/d, ad = bc
For any two nonzero real numbers, the reciprocal (or minus-one power) of their product is equal to the product of their reciprocals. If a and b are both nonzero real numbers:
1/(ab) = (1/a)(1/b)
(ab)–1 = a–1b–1
The product of two quotients or ratios, expressed as fractions, is equal to the product of their numerators divided by the product of their denominators. For all real numbers a, b, c, and d, where b ≠ 0 and d ≠ 0:
(a/b)(c/d) = (ac)/(bd)
For any two nonzero real numbers, the reciprocal (or minus-one power) of their quotient or ratio is equal to the quotient inverted or the ratio reversed. If a and b are real numbers where a ≠ 0 and b ≠ 0:
1/(a/b) = b/a
(a/b)–1 = b/a
The following general laws of arithmetic can be useful from time to time. You don’t really have to memorize them, as long as you can look them up when you need them. (But if you want to memorize them, go right ahead.)
The quotient or ratio of two products can be rewritten as a product of two quotients or ratios. For all real numbers a, b, c, and d, where cd ≠ 0:
(ab)/(cd) = (a/c)(b/d)
= (a/d)(b/c)
The quotient or ratio of two quotients or ratios can be rewritten either as a product of two quotients or ratios, or as the quotient or ratio of two products. For all real numbers a, b, c, and d, the following equations hold as long as b ≠ 0, c ≠ 0, and d ≠ 0:
(a/b)/(c/d) = (a/b)(d/c)
= (a/c)(d/b)
= (ad)/(bc)
If two quotients or ratios have the same nonzero denominator, their sum is equal to the sum of the numerators, divided by the denominator. For all real numbers a, b, and c, where c ≠ 0:
a/c + b/c = (a+ b)/c
If two quotients or ratios have different nonzero denominators, their sum must be found using a specific formula. For all real numbers a, b, c, and d, where b ≠ 0 and d ≠ 0:
a/b + c/d = (ad + bc)/(bd)
Suppose that a is a positive real number. Also suppose that n is a positive integer. Then the nth root of a can also be expressed as the 1/n power of a. Thus, the second root (or square root) is the same thing as the 1/2 power; the third root (or cube root) is the same thing as the 1/3 power; the fourth root is the same thing as the 1/4 power; and so on.
Suppose that a is a real number. Also suppose that b is a rational number such that b = m/n, where m and n are integers and n ≠ 0. Then the following formula holds:
ab = am/n = (am)1/n = (a1/n)m
Suppose that a is a real number. Also suppose that b is a rational number. Then the following formula holds:
a–b = (1/a)b = 1/(ab)
Suppose that a is a real number. Also suppose that b and c are rational numbers. Then the following formula holds:
a(b+c) = abac
Suppose a is a nonzero real number. Also suppose that b and c are rational numbers. Then the following formula holds:
a(b–c) = ab/ac
In mathematical literature, the expression “Let such-and-such be the case” is often used instead of “Suppose that such-and-such is true” or “Imagine such-and-such.” When you are admonished to “let” things be a certain way, you are in effect being asked to imagine, or suppose, that they are so. That’s the way the next few principles are stated. Also, different variables are used in the next few statements: x replaces a, y replaces b, and z replaces c. It’s a good idea to get used to this sort of variability (along with repetitiveness, ironically) to arm your mind against the assaults of mathematical discourse.
Let x be a real number. Let y and z be rational numbers. Then the following formula holds:
xyz = (xy)z = (xz)y
Let x be a real number. Let y and z be rational numbers, with the constraint that z ≠ 0. Then the following formula holds:
xy/z =(xy)1/z
POWER OF RECIPROCAL
Let x be a nonzero real number. Let n be a natural number. Then the nth power of the reciprocal of x is equal to the reciprocal of x to the nth power. That is:
(1/x)n = 1/(xn)
Let x and y be real numbers. Then the following formulas hold:
(x + y)2 = x2 + 2xy + y2
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
Let x and y be real numbers. Then the following formulas hold:
(x – y)2 = x2 – 2xy + y2
(x – y)3 = x3 – 3x2y + 3xy2 – y3
(x – y)4 = x4 – 4x3y + 6x2y2 – 4xy3 + y4
What is the value of (1/27)1/3?
We are seeking the 1/3 power (or the cube root) of 1/27. This means we are looking for some number which, when multiplied by itself and then multiplied by itself again, will produce 1/27.
Imagine some number y such that (1/y)3 = (1/y)(1/y)(1/y) = 1/27. Then y must be the cube root of 27. Using a calculator, the cube root of 27 is found to be 3. From this we can conclude that 1/y = 1/3, and thus that (1/3)3 = 1/27. The value we seek, the cube root (or 1/3 power) of 1/27, is therefore 1/3.
Find the sum of 2/7 and –5/8.
Use the formula for the sum of quotients in general, stated earlier in this chapter. As long as b and d are nonzero, the following holds for all real numbers a, b, c, and d:
a/b+ c/d = (ad + bc)/(bd)
Assign a = 2, b = 7, c = –5, and d = 8. Then plug the numbers into the formula:
2/7 + (–5/8) = [(2 × 8) + (7 × –5)]/(7 × 8)
= [16 + (–35)]/56
= –19/56
Refer to the text in this chapter if necessary. A good score is eight correct. Answers are in the back of the book.
1. The reciprocal of a number is the same thing as the
(a) additive inverse
(b) exponent
(c) minus-one power
(d) cube root
2. What is the value of –24 × 3 + 2?
(a) –46
(b) 50
(c) 80
(d) This expression is ambiguous without parentheses to tell us the precedence of the operations.
3. The sum of 3/x and 5/x, where x represents any real number other than 0, is
(a) 8/(x2)
(b) 8/(2x)
(c) 8/x
(d) 15/x
4. The square of b/4, where b represents any rational number, is
(a) b2/4
(b) b2/8
(c) b2/16
(d) bb/256
5. Figure 1-5 is called a Venn diagram. It denotes sets as circular regions (including their interiors) on a surface. What does the shaded region in this illustration represent?
(a) A + B
(b) A ∩ B
(c) A ∪ B
(d) A ⊆ B
6. In Fig. 1-5, the objects labeled P, Q, and R represent individual points. Which of the following statements is true?
(a) P ∈ (A ∪ B)
(b) Q ∈ (A ∩ B)
(c) R ∈ Ø
(d) P ⊂ A
7. Suppose q, r, and s represent real numbers. Which of the following statements is not true in general, unless constraints are imposed on one or more of the variables?
(a) q(r + s) = qr qs
(b) q/s – r/s = (q – r)/s
(c) (q + r) + s = q + (r + s)
(d) (qr)s = q(rs)
8. When we write 34.34343434. . ., we are writing a representation of
(a) an irrational number
(b) a nonterminating, nonrepeating decimal
(c) a nondenumerable number
(d) a rational number
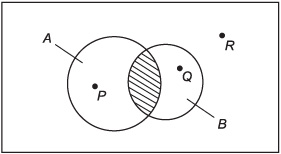
Fig. 1-5. Illustration for Quiz Questions 5 and 6.
9. The 1/2 power of a number is the same thing as
(a) the square root of that number
(b) half of that number
(c) the number minus 1/2
(d) nothing; it is not defined
10. Suppose x, y, and z are positive real numbers. What is the value of x(y–z) when y = z?
(a) 0
(b) 1
(c) x
(d) It is not defined.