Numbers by themselves are abstract. Units make numbers concrete. We can say that a quantity is this wide, is that heavy, lasts this long, or is that hot; it extends for this many millimeters, weighs that many pounds, lasts this many hours, or is heated to that many degrees Celsius. Some of the material in this chapter might at first seem too scientific to be considered “everyday math.” But when it comes to math, it’s always important to know precisely what you mean when you say something. After you’ve gone through this material, nobody will be able to legitimately say that you don’t know what you’re talking about when you quote units of measurement.
There are various systems of physical units. The meter/kilogram/second (mks) system, also called the metric system and which is essentially the same as the International System, is favored in most of the developed world. The centimeter/gram/second (cgs) system is less often used. The foot/pound/second (fps) system, also called the English system, is popular among nonscientists in the United States. Each system has several fundamental, or base, units from which all the others are derived.
The International System is abbreviated SI (for the words Système International in French). This scheme in its earlier form, mks, has existed since the 1800s, but was more recently defined by the General Conference on Weights and Measures.
The base units in SI quantify displacement, mass, time, temperature, electric current, brightness of light, and amount of matter. Respectively, the units in SI are known as the meter, the kilogram, the second, the Kelvin (or degree Kelvin), the ampere, the candela, and the mole.
In the centimeter/gram/second (cgs) system, the base units are the centimeter (exactly 0.01 meter), the gram (exactly 0.001 kilogram), the second (identical to the SI second), the degree Celsius (approximately the number of Kelvins minus 273.15), the ampere (identical to the SI ampere), the candela (identical to the SI candela), and the mole (identical to the SI mole).
In the English or fps system, the base units are the foot (approximately 30.5 centimeters), the pound (equivalent to about 2.2 kilograms in the gravitational field at the earth’s surface), and the second (identical to the SI second). Other units include the degree Fahrenheit (where water freezes at 32 degrees and boils at 212 degrees at standard sea-level atmospheric pressure), the ampere (identical to the SI ampere), the candela (identical to the SI candela), and the mole (identical to the SI mole).
In all systems of measurement, the base units are those from which all the others can be derived. Base units represent some of the most elementary properties or phenomena we observe in nature.
The fundamental unit of distance, length, linear dimension, or displacement (all these terms mean essentially the same thing) is the meter, symbolized by the non-italicized, lowercase English letter m.
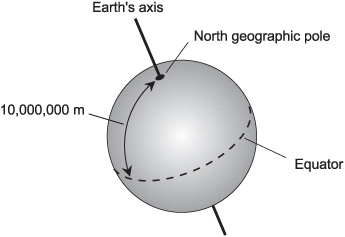
The original definition of the meter was based on the notion of dividing the shortest possible surface route between the north pole and the equator of the earth, as it would be measured if it passed through Paris, France (Fig. 4-1), into 10 million (107) identical units. Mountains, bodies of water, and other barriers were ignored; the earth was imagined to be a perfectly round, smooth ball. The circumference of the earth was therefore determined to be 40 million (4.000 × 107) m, give or take a little depending on which great circle around the globe one happened to choose.
Nowadays, the meter is defined more precisely as the distance a beam of light travels through a perfect vacuum in 1/299,792,458, or 3.33564095 × 10–9, of a second. This is approximately the length of an adult’s full stride when walking at a brisk pace, and is a little longer than an English yard.
Various units smaller or larger than the meter are often employed to measure or define displacement. A millimeter (mm) is 0.001 m. A micrometer

Fig. 4-1. There are about 10,000,000 meters between the earth’s north pole and the equator.
(μm or μ) is 0.000001m or 10–6m. Sometimes the micrometer is called the micron, but that term is technically out-of-date. A nanometer (nm) is 10–9 m. A kilometer (km) is 1000 m.
The base SI unit of mass is the kilogram, symbolized by the lowercase, non-italicized pair of English letters kg.
Originally, the kilogram was defined as the mass of a cube of pure liquid water measuring exactly 0.1m on each edge (Fig. 4-2). That is still an excellent definition, but these days, scientists have come up with something more absolute. A kilogram is the mass of a sample of platinum–iridium alloy that is kept at the International Bureau of Weights and Measures. This object is called the international prototype of the kilogram.
It’s important to realize that mass is not the same thing as weight. A mass of 1 kg maintains this same mass no matter where it is located. That standard platinum–iridium ingot would have a mass of 1 kg on the moon, on Mars, or in intergalactic space. Weight, in contrast, is a force exerted by gravitation on a given mass. On the surface of the earth, a 1-kg mass happens to weigh about 2.2 pounds.
Various units smaller or larger than the kilogram are used to measure or define mass. A gram (g) is 0.001 kg. A milligram (mg) is 0.000001 kg or 10–6kg. A microgram (μg) is 10–9 kg. A nanogram (ng) is 10–12g. A metric ton is 1000 kg.
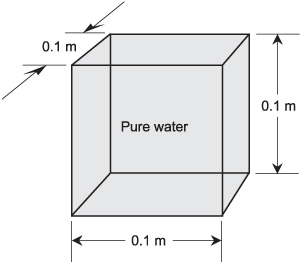
Fig. 4-2. Originally, the kilogram was defined as the mass of 0.001 cubic meter of pure liquid water.
The SI unit of time is the second, symbolized by the lowercase, non-italic English letter s. Sometimes it is abbreviated using its first three letters, sec.
The second was originally defined as exactly 1/60 of a minute, which is exactly 1/60 of an hour, which in turn is exactly 1/24 of a mean solar day. (The solar day is defined as the length of time it takes for the sun to pass from due south to due south again as observed from the earth’s northern hemisphere; the mean solar day is the average length of all the solar days in a year.) A second was thought of as 1/86,400 of a mean solar day, and that is still an excellent definition (Fig. 4-3). But more recently, with the availability of atomic time standards, 1 s has been formally defined as the amount of time taken for a certain isotope of elemental cesium to oscillate through 9,192,631,770 (9.192631770 × 109) complete cycles.
A second happens to be the time it takes for a ray of light to travel 2.99792458 × 108 m through space. This is about three-quarters of the way to the moon. You might have heard of the moon being a little more than one light-second away from earth. If you are old enough to remember the conversations earth-based personnel carried on with Apollo astronauts as the space travelers walked around on the moon, you will recall the delay between comments or questions from earthlings and replies from the moonwalkers.
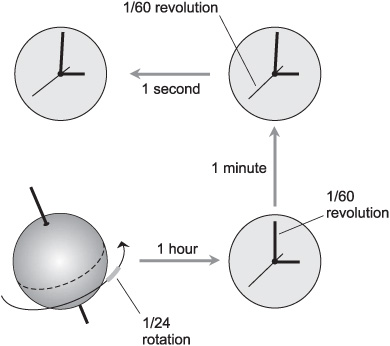
Fig. 4-3. Originally, the second was defined as (1/60)(1/60)(1/24), or 1/86,400, of a mean solar day.
The astronauts were not hesitating; it took more than 2 s for radio signals to make a round trip between the earth and moon.
Units smaller than the second are often employed to measure or define time. A millisecond (ms) is 0.001 s; a microsecond (μs) is 0.000001 s or 10–6s; a nanosecond (ns) is 10–9 s.
The SI unit of temperature is the Kelvin, symbolized K or °K (uppercase and non-italicized). It is a measure of how much heat exists relative to absolute zero, which represents the absence of all heat and which is therefore the coldest possible temperature. A temperature of 0 °K represents absolute zero. There are never any negative temperature readings on the Kelvin scale.
Formally, the Kelvin is defined as a temperature increment (an increase or decrease) of 1/273.16, or 0.0036609, part of the thermodynamic temperature of the triple point of pure water. The triple point of water is the temperature and pressure at which it can exist as vapor, liquid, and ice in equilibrium. It’s almost, but not exactly, the same as the freezing point. Pure water at sea level freezes (or melts) at +273.15°K, and boils (or condenses) at +373.15°K.
The ampere, symbolized by the non-italic, uppercase English letter A (or abbreviated as amp), is the unit of electric current. A flow of approximately 6.241506 × 1018 electrons per second, past a given fixed point in an electrical conductor, represents a current of 1 A.
Various units smaller than the ampere are often employed to measure or define current. A milliampere (mA) is 0.001 A, or a flow of 6.241506 × 1015 electrons per second past a given fixed point. A microampere (μA) is 0.000001 A or 10–6 A, or a flow of 6.241506 × 1012 electrons per second. A nanoampere (nA) is 10–9 A; it is the smallest unit of electric current you are likely to hear about. It represents a flow of 6.241506 × 109 electrons per second past a given fixed point.
The most rigorous definition of the ampere is highly theoretical: 1 A is the amount of constant charge-carrier flow through two straight, parallel, infinitely thin, perfectly conducting wires, placed 1 m apart in a vacuum, that results in a certain amount of force (2 × 10–7 newton) per meter of distance. The newton will be defined shortly.
The candela, symbolized by the non-italicized, lowercase pair of English letters cd, is the unit of luminous intensity. It is equivalent to 1/683 of a watt of radiant energy, emitted at a frequency of 5.40 × 1014 hertz (cycles per second), in a solid angle of 1 steradian. The watt and the steradian will be defined shortly.
There is a simpler, although crude, definition of the candela: 1 cd is roughly the amount of light emitted by an ordinary candle. (That’s why brightness used to be expressed in units called candlepower.) Yet another definition tells it this way: 1 cd represents the radiation from a surface area of 1.667 × 10–6 square meters of a perfectly-radiating object called a blackbody, at the solidification temperature of pure platinum.
The mole, symbolized or abbreviated by the non-italicized, lowercase English letters mol, is the standard unit of material quantity. It is also known as Avogadro’s number, and is a huge number, approximately equal to 6.022169 × 1023. This is the number of atoms in exactly 12 g (0.012 kg) of carbon 12, the most common isotope of elemental carbon with six protons and six neutrons in the nucleus.
The mole arises naturally in the physical world, especially in chemistry. It is one of those numbers for which the cosmos seems to have reserved a special place.
You’ll sometimes hear about units called millimoles (mmol) and kilomoles (kmol). A quantity of 1 mmol represents 0.001 mol or 6.022169 × 1020; a quantity of 1 kmol represents 1000 mol or 6.022169 × 1026. The mole is an example of a dimensionless unit because it does not express any particular physical phenomenon. It’s just a certain standardized number, like a dozen (12) or a gross (144).
The history of the International System of Units is interesting. The definitions of the base units have gone through a lot of evolution! If you want to know more, visit the following Web site (valid at the time of this writing):
http://physics.nist.gov/cuu/Units/history.html
If this URL (uniform resource locator) does not bring up the right information, or if the link is broken, bring up one of the popular search engines such as Google (http://www.google.com) or Yahoo (http://www.yahoo.com), and input “International System of Units” using the phrase-search feature.
Until now, we’ve been rigorous about mentioning that symbols and abbreviations consist of lowercase or uppercase, non-italicized letters or strings of letters. That’s important, because if this distinction is not made, especially relating to the use of italics, the symbols or abbreviations for physical units can be confused with the constants, variables, or coefficients that appear in equations.
When a letter is italicized, it almost always represents a constant, a variable, or a coefficient. When it is non-italicized, it often represents a physical unit or a prefix multiplier. A good example is s, which represents second, versus s, which is often used to represent linear dimension or displacement. Another example is m, representing meter or meters, as compared with m, which is used to denote the slope of a line in a graph.
From now on, we won’t belabor this issue every time a unit symbol or abbreviation comes up. But don’t forget it. Like the business about significant figures, this seemingly trivial thing can matter a lot!
Suppose a pan of water is heated uniformly at the steady rate of 0.001 °K per second from 290 °K to 320 °K. (Water is a liquid at these temperatures on the earth’s surface.) Draw a graph of this situation, where time is the independent variable and is plotted on the horizontal axis, and temperature is the dependent variable and is plotted on the vertical axis for values between 311 °K and 312 °K only. Optimize the time scale.
The optimized graph is shown in Fig. 4-4. Note that it’s a straight line, indicating that the temperature of the water rises at a constant rate. Because a change of only 0.001 °K takes place every second, it takes 1000 seconds for the temperature to rise the 1 °K from 311 °K to 312 °K. The time scale is therefore graduated in relative terms from 0 to 1000.
Draw a “zoomed-in” version of the graph of Fig. 4-4, showing only the temperature range from 311.30 °K to 311.40 °K. Use a relative time scale, starting at 0. Again, optimize the time scale.
See Fig. 4-5. The line is in the same position on the coordinate grid as the one shown in the previous example. The scales, however, have both been “magnified” or “zoomed-into” by a factor of 10.
How many electrons flow past a given point in 3.00 s, given an electrical current of 2.00 A? Express the answer to three significant figures.
From the definition of the ampere, we know that 1.00 A of current represents the flow of 6.241506 × 1018 electrons per second past a point per second
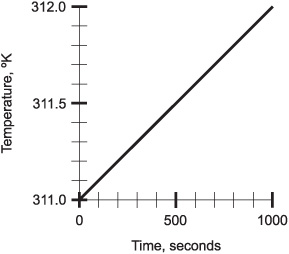
Fig. 4-4. Illustration for Problem 4-1.
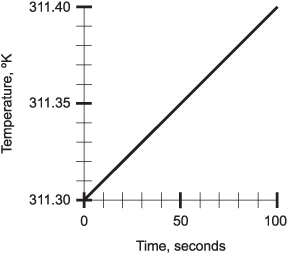
Fig. 4-5. Illustration for Problem 4-2.
of time. Therefore, a current of 2.00 A represents twice this many electrons, or 1.2483012 × 1019, flowing past the point each second. In 3.00 seconds, three times that many electrons pass the point. That’s 3.7449036 × 1019 electrons. Rounding off to three significant figures, we get the answer: 3.74 × 1019 electrons pass the point in 3.00 s.
The preceding seven units can be combined to generate many other units. Sometimes, the so-called derived units are expressed in terms of the base units, although such expressions can be confusing (for example, seconds cubed or kilograms to the minus-one power). If you ever come across combinations of units that seem nonsensical, don’t be alarmed. You are looking at a derived unit that has been put down in terms of base units.
The standard unit of plane angular measure is the radian (rad). It is the angle subtended by an arc on a circle, whose length, as measured on the circle, is equal to the radius of the circle as measured on a flat geometric plane containing the circle. Imagine taking a string and running it out from the center of a circle to some point on the edge, and then laying that string down around the periphery of the circle. The resulting angle is 1 rad. Another definition goes like this: one radian is the angle between the two straight edges of a slice of pie whose straight and curved edges all have the same length r (Fig. 4-6). It is equal to about 57.2958 angular degrees.
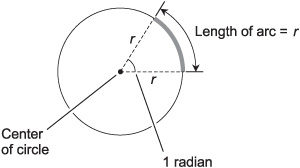
Fig. 4-6. One radian is the angle at the apex of a slice of pie whose straight and curved edges all have the same length r.
The angular degree, symbolized by a little elevated circle (°) or by the three-letter abbreviation deg, is equal to 1/360 of a complete circle. The history of the degree is uncertain, although one theory says that ancient mathematicians chose it because it represents approximately the number of days in the year. One angular degree is equal to approximately 0.0174533 radians.
The standard unit of solid angular measure is the steradian, symbolized sr. A solid angle of 1 sr is represented by a cone with its apex at the center of a sphere, intersecting the surface of the sphere in a circle such that, within the circle, the enclosed area on the sphere is equal to the square of the radius of the sphere (Fig. 4-7). There are 4π, or approximately 12.56636, steradians in a complete sphere.
The standard unit of mechanical force is the newton, symbolized N. One newton is the amount of force that it takes to make a mass of 1 kg accelerate at a rate of one meter per second squared (1 m/s2). Jet or rocket engine
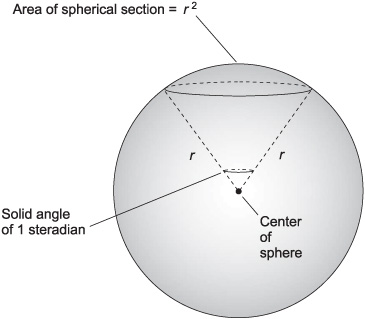
Fig. 4-7. One steradian is a solid angle that defines an area on a sphere equal to the square of the radius of the sphere.
propulsion is measured in newtons. Force is equal to the product of mass and acceleration; reduced to base units in SI, newtons are equivalent to kilogram-meters per second squared (kg · m/s2).
The standard unit of energy is the joule, symbolized J. This is a small unit in real-world terms. One joule is the equivalent of a newton-meter (N · m). If reduced to base units in SI, the joule can be expressed in terms of unit mass multiplied by unit distance squared per unit time squared:
1J = 1kg · m2/s2
The standard unit of power is the watt, symbolized W. One watt is equivalent to one joule of energy expended per second of time (1 J/s). Power is a measure of the rate at which energy is produced, radiated, or consumed. The expression of watts in terms of SI base units begins to get esoteric:
1W = 1kg · m2/s3
You won’t often hear about an electric bulb being rated at “60 kilogram-meters squared per second cubed,” but technically, this is equivalent to saying that the bulb is rated at 60 W.
Various units smaller or larger than the watt are often employed to measure or define power. A milliwatt (mW) is 0.001 W. A microwatt (μW) is 0.000001 W or 10–6 W. A nanowatt (nW) is 10–9 W. A kilowatt (kW) is 1000W. A megawatt (MW) is 1,000,000W or 106 W.
The standard unit of electric charge quantity is the coulomb, symbolized C. This is the electric charge that exists in a congregation of approximately 6.241506 × 1018 electrons. It also happens to be the electric charge contained in that number of protons, anti-protons, or positrons (anti-electrons). When you walk along a carpet with hard-soled shoes in the winter, or anywhere the humidity is very low, your body builds up a static electric charge that can be expressed in coulombs (or more likely a fraction of one coulomb). Reduced to base units in SI, one coulomb is equal to one ampere-second (1 A · s).
The coulomb, like the mole, is a dimensionless unit. It represents a numeric quantity. In fact, 1 C is equivalent to approximately 1.0365 × 10–5 mol. The coulomb is always used in reference to quantity of particles that carry a unit electric charge; but that is simply a matter of convention.
The standard unit of electric potential or potential difference, also called electromotive force (EMF), is the volt, symbolized V. One volt is equivalent to one joule per coulomb (1 J/C). The volt is, in real-world terms, a moderately small unit of electric potential.
A standard dry cell of the sort you find in a flashlight (often erroneously called a “battery”), produces about 1.5 V. Most automotive batteries in the United States produce between 12 V and 13.5 V. Some high-powered radio and audio amplifiers operate with voltages in the hundreds or even thousands.
You’ll sometimes encounter expressions of voltage involving prefix multipliers. A millivolt (mV) is 0.001 V. A microvolt (μV) is 0.000001 V or 10–6 V. A nanovolt (nV) is 10–9 V. A kilovolt (kV) is 1000 V. A megavolt (MV) is 1,000,000 V or 106 V.
The standard unit of electrical resistance is the ohm, symbolized by the uppercase Greek letter omega (Ω) or sometimes simply written out in full as “ohm.” Resistance is mathematically related to the current and the voltage in any direct-current (dc) electrical circuit.
When a current of 1 A flows through a resistance of 1 Ω a voltage of 1 V appears across that resistance. If the current is doubled to 2 A and the resistance remains at 1 Ω, the voltage doubles to 2 V; if the current is cut by a factor of 4 to 0.25 A, the voltage likewise drops by a factor of 4 to 0.25 V. The ohm is thus equivalent to a volt per ampere (1 V/A).
The ohm is a small unit of resistance, and you will often see resistances expressed in units of thousands or millions of ohms. A kilohm (kΩ or k) is 1000Ω a megohm (MΩ or M) is 1,000,000 Ω.
The standard unit of frequency is the hertz, symbolized Hz. It was formerly called the cycle per second or simply the cycle. If a wave has a frequency of 1 Hz, it goes through one complete cycle every second. If the frequency is 2 Hz, the wave goes through two cycles every second, or one cycle every 1/2 second. If the frequency is 10 Hz, the wave goes through 10 cycles every second, or one cycle every 1/10 second.
The hertz is used to express audio frequencies, for example the pitch of a musical tone. The hertz is also used to define the frequencies of wireless signals, both transmitted and received. It can even represent signal bandwidth.
The hertz is a small unit in the real world, and 1 Hz represents an extremely low frequency. More often, you will hear about frequencies that are measured in thousands, millions, billions (thousand-millions), or trillions (million-millions) of hertz. These units are called kilohertz (kHz), megahertz (MHz), gigahertz (GHz), and terahertz (THz), respectively.
In terms of SI units, the hertz is mathematically simple, but the concept is esoteric for some people to grasp: it is an “inverse second” (s–1) or “per second” (/s).
It has been said that the clock speed of the microprocessor in an average personal computer doubles every year. Suppose that is precisely true, and continues to be the case for at least a decade to come. If the average microprocessor clock speed on January 1, 2005 is 10 GHz, what will be the average microprocessor clock speed on January 1, 2008?
The speed will double 3 times; that means it will be 23, or 8, times as great. Thus, on January 1, 2008, the average personal computer will have a microprocessor rated at 10 GHz × 8 = 80 GHz.
In the preceding scenario, what will be the average microprocessor clock speed on January 1, 2015?
In this case the speed will double 10 times; it will become 210, or 1024, times as great. That means the speed will be 10 GHz × 1024, or 10,240 GHz. This is better expressed as 10.240 THz which, because we are told the original speed to only two significant figures, is best rounded to an even 10 THz.
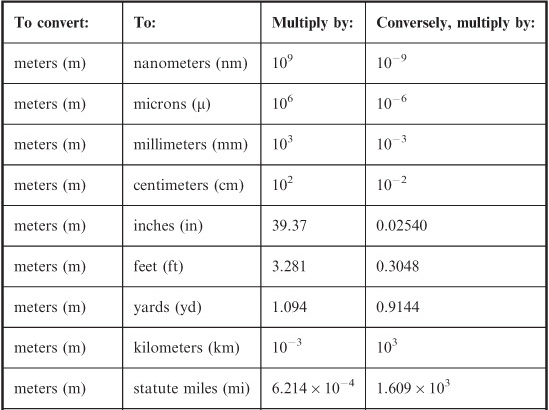
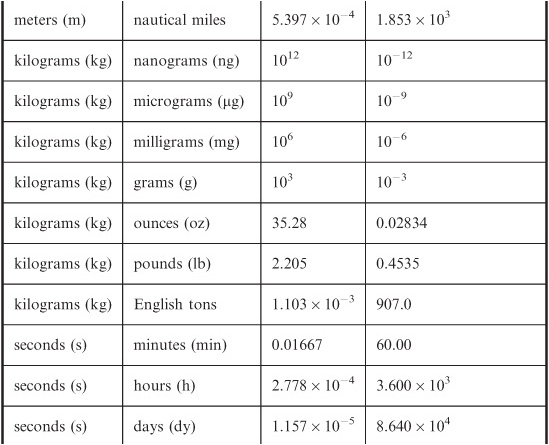
With all the different systems of units in use throughout the world, the business of conversion from one system to another has become the subject matter for Web sites. Nevertheless, in order to get familiar with how units relate to each other, it’s a good idea to do a few manual calculations before going online and letting your computer take over the “dirty work.” The problems below are some examples; you can certainly think of other unit-conversion situations that you are likely to encounter in your everyday affairs. Table 4-1 can serve as a guide for converting base units.
When converting from one unit system to another, always be sure you’re talking about the same quantity or phenomenon. For example, you cannot convert meters squared to centimeters cubed, or candela to meters per second. You must keep in mind what you’re trying to express, and be sure you are not, in effect, trying to change an apple into a drinking glass.
The particular thing that a unit quantifies is called the dimension of the quantity or phenomenon. Thus, meters per second, feet per hour, and furlongs per fortnight represent expressions of the speed dimension; seconds, minutes, hours, and days are expressions of the time dimension.
Suppose you step on a scale and it tells you that you weigh 120 pounds. How many kilograms does that represent?
Assume you are on the planet earth, so your mass-to-weight conversion can be defined in a meaningful way. (Remember, mass is not the same thing as weight.) Use Table 4-1. Multiply by 0.4535 to get 54.42 kg. Because you are given your weight to only three significant figures, you should round this off to 54.4 kg.
You are driving in Europe and you see that the posted speed limit is 90 kilometers per hour (km/hr). How many miles per hour (mi/hr) is this?
In this case, you only need to worry about miles versus kilometers; the “per hour” part doesn’t change. So you convert kilometers to miles. First remember that 1km = 1000m; then 90km = 90,000m = 9.0 × 104m. The conversion of meters to statute miles (these are the miles used on land) requires that you multiply by 6.214 × 10–4. Therefore, you multiply 9.0 × 104 by 6.214 × 10–4 to get 55.926. This must be rounded off to 56, or
Table 4-1 Conversions for base units in the International System (SI) to units in other systems. When no coefficient is given, it is exactly equal to 1.
two significant figures, because the posted speed limit quantity, 90, only goes that far.
How many feet per second is the above-mentioned speed limit? Use the information in Table 4-1.
Let’s convert kilometers per hour to kilometers per second first. This requires division by 3600, the number of seconds in an hour. Thus, 90km/hr = 90/3600 km/s = 0.025 km/s. Next, convert kilometers to meters. Multiply by 1000 to obtain 25m/s as the posted speed limit. Finally, convert meters to feet. Multiply 25 by 3.281 to get 82.025. This must be rounded off to 82 ft/sec because the posted speed limit is expressed to only two significant figures.
Refer to the text in this chapter if necessary. A good score is eight correct. Answers are in the back of the book.
1. Which of the following terms commonly represents more than one measurable quantity or phenomenon?
(a) meter
(b) pound
(c) radian
(d) degree
2. The mole is a unit that expresses the
(a) number of electrons in an ampere
(b) number of particles in a sample
(c) distance from the sun to a planet
(d) time required for an electron to orbit an atomic nucleus
3. The nomograph of Fig. 4-8 can be used to convert:
(a) feet to meters
(b) inches to centimeters
(c) miles to kilometers
(d) grams to pounds
4. A joule is the equivalent of a
(a) foot-pound
(b) meter per second
(c) kilogram per meter
(d) watt-second

Fig. 4-8. Illustration for Quiz Question 3.
5. An example of a dimensionless unit is
(a) the kilogram
(b) the meter
(c) the second
(d) none of the above
6. Force is equivalent to
(a) mass multiplied by distance
(b) mass multiplied by time
(c) mass multiplied by acceleration
(d) mass multiplied by speed
7. Two islands are 1345 nautical miles apart. How many kilometers is this?
(a) 2492
(b) 2164
(c) 1853
(d) It is impossible to say without more information.
8. The number of kilograms an object has can be converted to pounds only if you also know the
(a) temperature of the object
(b) size of the object
(c) gravitational strength on the planet where the object is located
(d) number of moles of atoms in the object
9. The pound is a unit of
(a) mass
(b) distance
(c) acceleration
(d) none of the above
10. The SI system is an expanded form of the
(a) English system
(b) metric system
(c) European system
(d) American system