When the variable, or unknown, in an equation is raised to a power, things get interesting. The larger the exponents attached to the variables, the more interesting things become, and the more difficult it gets to solve the equation. In this chapter, we’ll look into the basics of quadratic, cubic, and higher-order equations in one variable. Even if you’re not a mathematician or a scientist, you’ll encounter equations like these once in a while, so it’s good to know about them.
A one-variable, second-order equation, also called a second-order equation in one variable or, more often, a quadratic equation, can be written in the following standard form:
ax2 + bx + c = 0
where a, b, and c are constants, a is not equal to 0, and x is the variable. The constants a, b, and c are also known as coefficients.
Any equation that can be converted into the above form is a quadratic equation. Alternative forms are:
mx2 + nx = p
qx2 = rx + s
(x + t)(x + u) = 0
where m, n, p, q, r, s, t, and u are constants. Here are some examples of quadratic equations in various forms:
x2 + 2x + 1 = 0
–3x2 – 4x = 2
4x2 = –3x + 5
(x + 4)(x - 5) = 0
Some quadratic equations are easy to solve. Others are difficult. The first step in finding the value(s) of the variable in a quadratic is to get the equation either into standard form or into factored form.
The first equation above is already in standard form. It is ready for an attempt at solution, which, as we will shortly see, is easy.
The second equation above can be reduced to standard form by subtracting 2 from each side:
–3x2 – 4x = 2
–3x2 –4x –2 = 0
The third equation above can be reduced to standard form by adding 3x to each side and then subtracting 5 from each side:
4x2 = –3x + 5
4x2+ 3x = 5
4x2 + 3x – 5 = 0
An interesting aside: these are not the only ways the equations can be reduced to standard form. They can be multiplied through by any nonzero constant, and the resulting equations are still in standard form.
The fourth equation above is in factored form. This is a convenient form, because a quadratic equation denoted this way can be solved without having to do any work. Look at it closely:
(x + 4)(x – 5) = 0
The expression on the left-hand side of the equals sign is zero if either of the two factors is zero. If x = –4, then here is what happens when we “plug it in”:
(– 4 + 4)(– 4 – 5) = 0
0 x –9 = 0 (It works!)
If x = 5, then here’s what occurs:
(5 + 4)(5 – 5) = 0
9 x 0 = 0 (It works again!)
It is obvious which values for the variable in a factored quadratic will work as solutions. Simply take the additive inverses (negatives) of the constants in each factor. It’s so easy, in fact, that you must think there’s a catch. There is, of course. Most quadratic equations are difficult to get neatly into factored form.
Here are a couple of little things that should be cleared up right away, so you never get confused about them.
Suppose you run across a quadratic like this:
x(x + 3) = 0
You might want to imagine this equation written out like this:
(x + 0)(x + 3) = 0
This makes it easy to see that the solutions are x = 0 or x = –3. Of course, adding 0 to a variable doesn’t change anything except to make an equation longer. But it can clarify the process of solving some equations.
In case you forgot, at the beginning of this section it was mentioned that a quadratic equation might have only one real-number solution. Here is an example of the factored form of such an equation:
(x – 11)(x – 11) = 0
In standard form, the equation looks like this:
x2 – 22x + 121 = 0
Some purists might say, “This equation has two real-number solutions, and they are both equal to 11.”
Convert the following quadratic equations into factored form with real-number coefficients:
x2 – 2x – 15 = 0
x2+ 4 = 0
The first equation turns out to have a “clean” factored equivalent:
(x + 3)(x – 5) = 0
The second equation does not have any real-numbered solutions, so the problem, as stated, can’t be solved. Getting the second equation into factored form requires that you know something about complex numbers, and we’ll get into that subject in a moment. You can tell that something is peculiar about this equation if you subtract 4 from each side:
x2 + 4 = 0
x2 = –4
No real number can be substituted for x in this equation in order to make it a true statement. That is because no real number, when squared, produces a negative real-number result.
Put the following factored equations into standard quadratic form:
(x + 5)(x – 1) = 0
x(x + 4) = 0
Both of these can be converted to standard form by multiplying the factors. In the first case, it can be done in two steps:
(x + 5)(x – 1) = 0
x2 – x + 5x + [5 x(–1)] = 0
x24x 5 = 0
In the second case, it can be done in a single step:
x(x + 4) = 0
x2+ 4x = 0
Examine these two quadratic equations:
–3x2 – 4x = 2
4x2= –3x + 5
These can be reduced to standard form:
–3x2 – 4x – 2 = 0
4x2 + 3x – 5 = 0
You might stare at these equations for a long time before you get any ideas about how to factor them. Eventually, you might wonder why you are wasting your time. These equations do not “want” to be factored. Fortunately, there is a formula you can use to solve quadratic equations in general.
Consider the general quadratic equation:
ax2+ bx+ c = 0
where a≠ 0. The solution(s) to this equation can be found using this formula:
x = [– b ± (b2 – 4ac)1/2]/2a
The symbol ± is read “plus-or-minus” and is a way of compacting two mathematical expressions into one. Written separately, the equations are:
x = [– b+ (b2 – 4ac)1/2]/2a
x = [– b– (b2 – 4ac)1/2]/2a
The fractional exponent means the 1/2 power, another way of expressing the square root.
Examine this equation once again:
–3x2 – 4x 2 = 0
The coefficients are as follows:
a = – 3
b = – 4
c = – 2
Plugging these numbers into the quadratic formula produces solutions, as follows:
x = {4 ± [(–4)2 –(4 x–3 x–2)]1/2}/(2 x–3)
= 4 ± (16 – 24)1/2/(– 6)
= 4 ± (– 8)1/2/(– 6)
We are confronted with the square root of -8 in the solution. What is this? It isn’t a real number, but how can we ignore it? We’ll look into this matter shortly. For now, let’s work out a couple of problems with quadratics involving only the real numbers.
When we substitute y for 0 in the standard form of a quadratic equation, and then graph the resulting relation with x on the horizontal axis and y on the vertical axis, we get a curve called a parabola.
Suppose we want to plot a graph of the following equation:
ax2 + bx+ c = y
First, we determine the coordinates of the following point (x0, y0):
x0 = –b/(2a)
y0 = c – b2/(4a)
This point represents the base point of the parabola; that is, the point at which the curvature is sharpest. Once this point is known, we must find four more points by “plugging in” values of x somewhat greater than and less than x0, and then determining the corresponding y-values. These x-values, call them x−2, x−1, x1, and x2, should be equally spaced on either side of x0, such that:
x−2 < x−1 < x0 < x1 < x2
x−1 – x−2 = x0 – x−1 = x1 – x0 = x2 – x1
This gives us five points that lie along the parabola, and that are symmetrical relative to the axis of the curve. The graph can then be inferred if the points are wisely chosen. Some trial and error might be required. If a > 0, the parabola opens upward. If a< 0, the parabola opens downward.
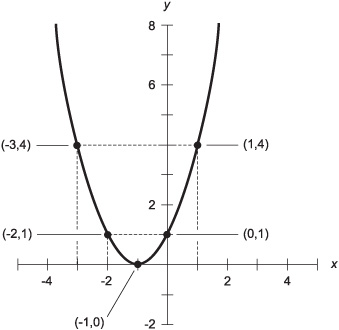
Plotting a parabola
Consider the following formula:
y = x2+ 2x + 1
Using the above formula to calculate the base point, we get this:
x0 = –2/2 = –1
y0 = 1 – 4/4 = 1 – 1 = 0
Therefore (x0, y0) = (–1,0)
We plot this point first, as shown in Fig. 6-1. Next, we plot points spaced at 1-unit horizontal-axis intervals on either side of x0, as follows:
x−2 = x0 – 2 = –3
y−2 = (–3)2 + 2 x (–3) + 1 = 9 – 6 + 1 = 4
Therefore (x−2, y−2) = (–3,4)

Fig. 6-1. Graph of the quadratic equation y = x2 + 2x +1.
y−1 = (–2)2 + 2x (–2)+ 1 = 4 – 4 + 1 = 1
Therefore (x−1, y−1) = (–2,1)
x1 = x0 + 1 = 0
y1 = 02 + 2 x 0 + 1 = 0 + 0 + 1 = 1
Therefore (x1, y1) = (0, 1)
x2 = x0 + 2 = 1
y2 = 12 + 2 x 1 + 1 = 1 + 2 + 1 = 4
Therefore (x2, y2) = (1,4)
From these five points, the parabola can be inferred. It is shown as a solid, heavy curve in Fig. 6-1.
Plotting another parabola
Let’s try another example, this time with a parabola that opens downward. Consider the following formula:
y = – 2x2 + 4x - 5
The base point is:
x0 = – 4/– 4 = 1
y0 = – 5 – 16/(–8) = –5 + 2 = –3
Therefore (x0, y0) = (1,–3)
This point is plotted first, as shown in Fig. 6-2. Next, we plot the following points:
x−2 = x0 –2 = –1
y−2 = –2 x (–1)2 + 4 x (–1) –5 = –2 – 4 – 5 = –11
Therefore (x−2, y−2) = (-1,-11)
Fig. 6-2. Graph of the quadratic equation y = –2x2 + 4x – 5.
x−1 = x0 –1 = 0
y−1 = –2 x 02 + 4 x 0 – 5 = –5
Therefore (x−1, y−1) = (0, – 5)
x1 = x0 + 1 = 2
y1 = – 2 x 22 + 4 x 2 – 5 = –8 + 8 – 5 = –5
Therefore (x1, y1) = (2, –5)
x2 = x0 + 2 – 3
y2 = –2 x 32 + 4 x 3 – 5 = –18 + 12 – 5 = –11
Therefore (x2, y2) = (3, – 11)
From these five points, the parabola is inferred. It is the solid, heavy curve in Fig. 6-2.
PROBLEM 6-3
Find the real-number solution(s) to the following equation by factoring:
x2 + 14x + 49 = 0
Assuming this equation can be put into factored form, let’s suppose the equation looks like this:
(x + t)(x + u) = 0
In this case, the solutions are x = – t and x = – u. The trick is finding t and u such that we get the original equation when the factors are multiplied together. The above generalized equation looks like this when multiplied out:
(x + t)(x + u) = 0
x2 + ux + tx + tu = 0
x2 +(u + t)x + tu = 0
Are there any numbers t and u whose sum equals 14 and their product equals 49? It should not take you long to see that the answer is yes; this works out if t = 7 and u = 7. If we substitute these values into the generalized, factored quadratic and then multiply it out, we get the original equation that we want to solve:
(x + 7)(x + 7) = 0
x2 + 7x + 7x + 49 = 0
x2 + 14x + 49 = 0
Therefore, there is a single real-number solution to this equation: x = –7.
Use the quadratic formula to solve the equation from the previous problem.
Here is the equation in standard form again:
x2 + 14x + 49 = 0
The coefficients from the general form, and which are defined in the quadratic formula above, are as follows:
a = 1
b = 14
c = 49
Here is what happens when we plug these coefficients into the quadratic formula:
x = {–14 ± [(14)2 = (4 x 1 x 49)]1/2}/(2 x 1)
= [–14 ± (196 – 196)1/2]/2
= (–14 ± 01/2)/2
= – 14/2
= -7
Mathematicians symbolize the positive square root of —1, called the unit imaginary number, by using the lowercase italic letter i. Scientists and engineers symbolize it using the letter j, and henceforth, we will too.
Any imaginary number can be obtained by multiplying j by some real number q. The real number q is customarily written after j if q is positive or zero. If q happens to be a negative real number, then the absolute value of q is written after –j. Examples of imaginary numbers are j3, –j5, j2.787, and –jπ.
The set of imaginary numbers can be depicted along a number line, just as can the real numbers. The so-called imaginary number line is usually shown standing on end, that is, vertically (Fig. 6-3). In a sense, the real-number line and the imaginary-number line are fraternal twins. As is the case with human twins, these two number lines, although they share similarities, are independent. The sets of imaginary and real numbers have one value, 0, in common. Thus:
j0 = 0
A complex number consists of the sum of some real number and some imaginary number. The general form for a complex number k is:
k = p + jq
where p and q are real numbers.
Fig. 6-3. The imaginary number line is just like the real number line, except that it is “stood on end” and all the quantities are multiplied by j.
Mathematicians, scientists, and engineers denote the set of complex numbers by placing the real-number and imaginary-number lines at right angles to each other, intersecting at the points on both lines corresponding to 0. The result is a rectangular coordinate plane (Fig. 6-4). Every point on this plane corresponds to a unique complex number, and every complex number corresponds to a unique point on the plane.
Now that you know a little about complex numbers, you might want to examine the solution to the following equation again:
–3x2 – 4x – 2 = 0
Recall that the solution, derived using the quadratic formula, contains the quantity (-8)1/2. An engineer or physicist would write this as j81/2, so the solution to the quadratic is:
x = (4 ± j81/2)/(-6)
This can be simplified to the standard form of a complex number, and then reduced to the lowest fractional form. Step-by-step, the simplification process
Fig. 6-4. The complex number plane portrays real numbers on the horizontal axis and imaginary numbers on the vertical axis.
goes like this:
x = (4 ± j81/2)/(—6)
= 4/6 ± j[81/2/(—6)]
= 2/3 ± j[2 x 21/2/(—6)]
= 2/3 ± j[2/(—6)x 21/2]
= 2/3 ± j(—1/3 x 21/2)
= 2/3 ±[—j(1/3 x 21/2)]
= 2/3 ± j(1/3 x 21/2)
This might not look any “simpler” at first glance, but it’s good practice to state complex numbers in standard form, and reduced to lowest fractions. The last step, in which the minus sign disappears, is justified because adding a negative is the same thing as subtracting a positive, and subtracting a negative is the same thing as adding a positive.
The two complex solutions to the equation can be stated separately this way:
x = 2/3 + j(1/3 x 21/2)
or
x = 2/3 - j(1/3 x 21/2)
Solve the following equation using the quadratic formula:
x2 + 9 = 0
In standard form showing all three coefficients a, b, and c, the equation looks like this:
1x2 + 0x + 9 = 0
Thus the coefficients are:
a = 1
b = 0
c = 9
Plugging these numbers into the quadratic formula yields:
x = {-0 ± [02 – (4 x 1 x 9)]1/2}/(2 x 1)
= ± (-36)1/2/2
= ± j6/2
= ± j3
Write out the quadratic equation from the preceding problem in factored form.
This would be tricky if we didn’t already know the solutions. But we do, so it’s easy:
(x + j3)(x - j3) = 0
You can verify that this works by “plugging in” the solutions derived from the quadratic formula in the previous problem.
As the exponents in single-variable equations get bigger, finding the solutions becomes a more challenging business. In the olden days, a lot of insight, guesswork, and tedium was involved in solving such equations. Today, scientists have the help of computers, and when problems are encountered containing equations with variables raised to large powers, they just let a computer take over. The material here is presented so you won’t be taken aback if you ever come across one-variable, higher-order equations.
A cubic equation, also called a one-variable, third-order equation or a third-order equation in one variable, can be written in the following standard form:
ax3 + bx2 + cx + d = 0
where a, b, c, and d are constants, x is the variable, and a ≠ 0.
If you’re lucky, you’ll be able to reduce a cubic equation to factored form to find real-number solutions – r, – s, and – t:
(x + r)(x + s)(x + t) = 0
Don’t count on being able to factor a cubic equation. Sometimes it’s easy, but most of the time it is nigh impossible. There is a cubic formula that can be used in a manner similar to the way in which the quadratic formula is used for quadratic equations, but it’s complicated, and is beyond the scope of this discussion.
Plotting cubics
When we substitute y for 0 in the standard form of a cubic equation and then graph the resulting relation with x on the horizontal axis and y on the vertical axis, a curve with a characteristic shape results.
Figure 6-5 is a graph of the simplest possible cubic equation:
x3 = y
Fig. 6-5. Graph of the cubic equation x3 = y.
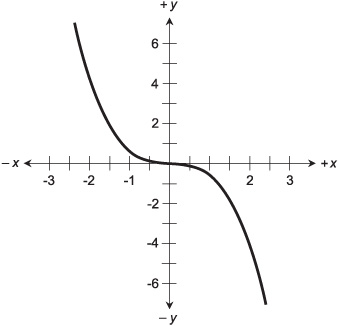
Fig. 6-6. Graph of the cubic equation (–1/2)x3 = y.
The domain and range of this function both encompass the entire set of real numbers. This makes the cubic curve different from the parabola, whose range is always limited to only a portion of the set of real numbers. Figure 6-6 is a graph of another simple cubic:
(–1/2)x3 = y
In this case, the domain and range also span all the real numbers.
The inflection point, or the place where the curve goes from concave downward to concave upward, is at the origin (0, 0) in both Fig. 6-5 and Fig. 6-6. This is because the coefficients b, c, and d are all equal to 0. When these coefficients are nonzero, the inflection point is not necessarily at the origin.
A quartic equation, also called a one-variable, fourth-order equation or a fourth-order equation in one variable, can be written in the following standard form:
ax4 + bx3 + cx2 + dx + e = 0
where a, b, c, d, and e are constants, x is the variable, and a≠ 0.
Once in a while you will be able to reduce a quartic equation to factored form to find real-number solutions –r, –s, –t, and –u:
(x + r)(x + s)(x + t)(x + u) = 0
As is the case with the cubic, you will be lucky if you can factor a quartic equation into this form and thus find four real-number solutions with ease.
Plotting quartics
When we substitute y for 0 in the standard form of a quartic equation and then graph the resulting relation with x on the horizontal axis and y on the vertical axis, a curve with a “parabola-like” shape is the result. But this curve is not a true parabola. It is distorted - flattened down in a sense - as can be seen when it is compared with a true parabola. The bends in the curve are sharper than those in the parabola, and the curve “takes off” more steeply beyond the bends.
Figure 6-7 is a graph of the simplest possible quartic equation:
x4 = y
The domain encompasses the whole set of real numbers, but the range of this function spans only the non-negative real numbers. Figure 6-8 is a graph of another simple quartic:
(–1/2)x4 = y
In this case, the domain spans all the real numbers, but the range spans only the non-positive real numbers.
You are welcome to “play around” with various quartic equations to see what their graphs look like. Their shapes, positions, and orientations can vary depending on the values of the coefficients b, c, d, and e.
Fig. 6-7. Graph of the quartic equation x4 = y.
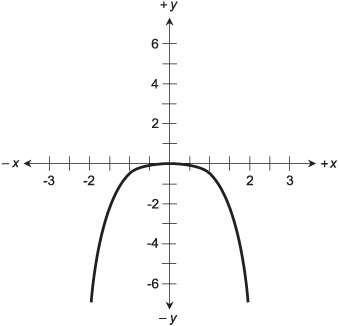
Fig. 6-8. Graph of the quartic equation (– 1/2)x4 = y.
A quintic equation, also called a one-variable, fifth-order equation or a fifth-order equation in one variable, can be written in the following standard form:
ax5 + bx4 + cx3 + dx2 + ex + f = 0
where a, b, c, d, e, and f are constants, x is the variable, and a ≠ 0.
There is a remote possibility that, if you come across a quintic, you’ll be able to reduce it to factored form to find real-number solutions – r, – s, – t, – u, and – v:
(x + r)(x + s)(x + t)(x + u)(x + v) = 0
As is the case with the cubic and the quartic, you will be lucky if you can factor a quintic equation into this form.
Plotting quintics
When we substitute y for 0 in the standard form of a quintic equation and then graph the resulting relation with x on the horizontal axis and y on the vertical axis, the resulting curve looks something like that of the graph of the cubic equation. The difference is that the bends are sharper, and the graphs run off more steeply toward “positive infinity” and “negative infinity” beyond the bends.
Figure 6-9 is a graph of the simplest possible quintic equation:
x5 = y
The domain and range of this function both span the set of reals. Figure 6-10 is a graph of another simple quintic:
(–1/2)x5 = y
In this case, the domain and range also span all the real numbers.
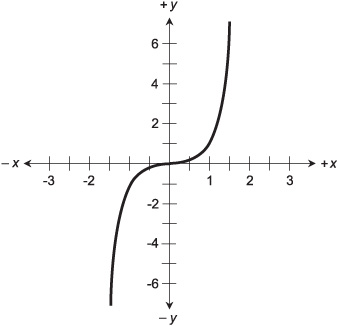
Fig. 6-9. Graph of the quintic equation x5 = y.
Fig. 6-10. Graph of the quintic equation (—1/2)x5 = y.
The inflection point for the graph of the quintic is at the origin in both Fig. 6-9 and Fig. 6-10. As in the case of equations of lower order that are shown in this chapter, the reason is that the coefficients other than a are all equal to 0.
A one-variable, nth-order equation can be written in the following standard form:
a1xn + a2xn–1 + a3xn–2 + . . . + an–2x2 + an–1x + an = 0
where a1, a2,. . .,an are constants, x is the variable, and a1 = 0. We won’t even think about trying to factor an equation like this in general, although specific cases might lend themselves to factorization. Solving nth-order equations, where n > 5, practically demands the use of a computer.
What happens to the general shape of the graph of the following equation if n is a positive even integer and n becomes larger without limit?
xn = y
If x– 0, then y– 0. If x = –1or x = 1, then y = 1. These two facts are true no matter what the value of n, as long as it is even. As n increases, the curve
Fig. 6-11. Illustration for Problem 6-7.
tends more and more toward 0 from the positive side when -1 < x <0 and when 0 < x < 1. Also, the curve rises ever-more-steeply toward “positive infinity” (+ ∞) when x < –1 or x> 1. Figure 6-11 is an approximate drawing of the graph of the equation x998 The bends are not perfectly squared-off, but they’re pretty close. The curve “takes off” in almost, but not perfectly, vertical directions.
What happens to the general shape of the graph of the following equation if n is a positive odd integer and n becomes larger without limit?
xn = y
If x = 0, then y = 0. If x = –1, then y = –1. If x = 1, then y = 1. These two facts are true regardless of the value of n, as long as it is odd. As n increases, the curve tends more and more toward 0 from the negative side when -1 < x < 0, and more and more toward 0 from the positive side when 0 < x < 1. The curve descends ever-more-steeply toward “negative infinity” (-∞) when x < -1, and rises ever-more-steeply toward “positive infinity” (+∞) when x > 1. Figure 6-12 is an approximate drawing of the graph of the equation x999 = y. As with the curve shown in Fig. 6-11, the “take-off” slopes are almost, but not quite, vertical.
Fig. 6-12. Illustration for Problem 6-8.
Refer to the text in this chapter if necessary. A good score is eight correct. Answers are in the back of the book.
1. A point on the graph of a function where the curve goes from concave upward to concave downward is called
(a) an inflection point
(b) a focal point
(c) a base point
(d) a slope point
2. The general form of a quadratic equation is:
ax2+ bx+ c = 0
Suppose a is a negative real number, b and c are real numbers, and (b2– 4ac) = 0. Then which of the following statements is true?
(a) The equation has a real-number solution.
(b) The equation has two different real-number solutions.
(c) The equation has no real-number solutions.
(d) The equation has no solutions at all.
3. The equation x5 = 3x2 + 2 is an example of
(a) a second-order equation
(c) a fourth-order equation
(d) a fifth-order equation
4. Which of the following equations has a graph that is not a parabola?
(a) x2 = y
(b) – x2 + 2x = y
(c) 5x2 - 2x + 4 = y
(d) 4x + 5 = y
5. In standard form, the factored equation (x – 10)(x + 10) = 0 is:
(a) x2 + 10x + 100 = 0
(b) x2 – 10x – 100 = 0
(c) x2 + 100 = 0
(d) x2 – 100 = 0
6. What is, or are, the real-number solutions of the equation (x – 10) (x + 10) = 0?
(a) –10
(b) 10
(c) –10 and 10
(d) There are none.
7. Which of the following numbers, when multiplied by itself, is equal to – 100?
(a) – 10
(b) 10
(c) j 10
(d) 10+ j 10
8. The domain of the function 2x3 - x2 + 4x + 2 = y consists of
(a) the set of real numbers greater than 2
(b) the set of real numbers smaller than 2
(c) the set of real numbers greater than or equal to 0
(d) the entire set of real numbers
9. Consider the following equation:
(x - 6)(x + j10)(x - 14)(x + j2) = 0
Which of the following numbers is not a solution to this equation?
(a) 6
(b) 14
(c) j2
(d) –j10
10. The solution(s) to the equation x2 – 2 = 0 is or are
(a) imaginary
(b) real, but irrational
(c) real and rational
(d) nonexistent