Do not refer to the text when taking this test. You may draw diagrams or use a calculator if necessary. A good score is at least 30 correct. Answers are in the back of the book. It’s best to have a friend check your score the first time, so you won’t memorize the answers if you want to take the test again.
1. Consider the following pair of equations, in which the intent is to find a solution or solutions, if any, for x and y simultaneously:
y = 3x + 4
y = 3x – 2
How many real-number solutions are there in this case?
(a) None.
(b) One.
(c) More than one.
(d) Infinitely many.
(e) More information is needed in order to answer this question.
2. In the complex number 2 + j3, the imaginary component consists of
(a) the number 2
(c) the number 2 multiplied by the square root of –1
(d) the number 3 multiplied by the square root of –1
(e) the product of 2 and 3, which is 6
3. In a frequency distribution, frequency is portrayed as the
(a) cumulative variable
(b) discrete variable
(c) dependent variable
(d) random variable
(e) continuous variable
4. What is the mathematical probability that a coin, tossed five times in a row, will come up “heads” on all five tosses?
(a) 1
(b) 1/2
(c) 1/5
(d) 1/25
(e) 1/32
5. Fill in the blank to make this sentence true: “A sample of a population is _________ of that population.”
(a) an expansion
(b) a subset
(c) a variance
(d) the average
(e) the median
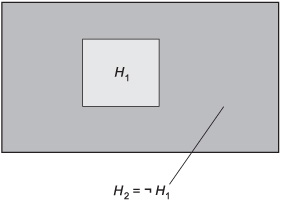
6. In Fig. Test 2-1, suppose H1 and H2 represent two different sets of outcomes in an experiment. The light-shaded region, labeled H1, represents
(a) the set of outcomes belonging to H1 but not to H2
(b) the set of outcomes belonging to neither H1 nor H2

Fig. Test 2-1. Illustration for Part Two Test Questions 6 through 9.
(c) the set of outcomes belonging to either H1 or H2, but not both
(d) the set of outcomes belonging to either H1 or H2, or both
(e) the set of outcomes belonging to H2 but not to H1
7. In Fig. Test 2-1, the dark-shaded region, labeled H2 = ¬H1, represents
(a) the set of outcomes common to both H1 and H2
(b) the set of outcomes belonging to neither H1 nor H2
(c) the set of outcomes belonging to either H1 or H2, but not both
(d) the set of outcomes belonging to either H1 or H2, or both
(e) the set of outcomes belonging to H2 but not to H1
8. In Fig. Test 2-1, the entire portion that is shaded, either light or dark, represents
(a) the set of outcomes common to both H1 and H2
(b) the set of outcomes belonging to neither H1 nor H2
(c) the set of outcomes belonging to either H1 or H2, but not both
(d) the empty set
(e) the set of outcomes belonging to H2 but not to H1
9. The Venn diagram of Fig. Test 2-1 portrays
(a) complementary outcomes
(b) mutually exclusive outcomes
(c) independent outcomes
(d) coincident outcomes
(e) nondisjoint outcomes
10. Which of the following is not an allowable maneuver to perform in solving a single-variable equation?
(a) Adding a constant to each side.
(b) Subtracting a constant from each side.
(c) Dividing each side by a variable that may attain a value of 0.
(d) Multiplying each side by a variable that may attain a value of 0.
(e) All of the above (a), (b), (c), and (d) are allowable.
11. What is the solution of the equation 3x + 5 = 2x – 4?
(a) There isn’t any.
(b) More information is needed in order to find out.
(c) 9
(d) –9
(e) 9 or –9
12. What is the mathematical probability that an “unweighted” die, tossed three times, will show the face with 2 dots on all three occasions?
(a) 1 in 6
(c) 1 in 64
(d) 1 in 216
(e) 1 in 46,656
13. What is the solution set of the equation x2 + 64 = 0?
(a) The empty set.
(b) {8}
(c) {8, –8}
(d) {j8, –j8}
(e) More information is needed to answer this.
14. Fill in the blank to make the following sentence true: “If the number of elements in a distribution is odd, then the __________ is the value such that the number of elements having values greater than or equal to it is the same as the number of elements having values less than or equal to it.”
(a) mean
(b) deviation
(c) frequency
(d) mode
(e) median
15. Let q represent a set of items or objects taken r at a time in a specific order. The possible number of permutations in this situation is symbolized qPr and can be calculated as follows:
qPr = q!/(q – r)!
Given this information, what is the possible number of permutations of 8 objects taken 2 at a time?
(a) 40,320
(b) 720
(c) 56
(d) 28
(e) 24
16. Let q represent a set of items or objects taken r at a time in no particular order, where q ≤ r, and where both q and r are positive integers. The possible number of combinations in this situation is symbolized qCr and can be calculated as follows:
qCr = q!/[r!(q – r)!]
Fig. Test 2-2. Illustration for Part Two Test Questions 17 through 19.
Given this information, what is the possible number of combinations of 8 objects taken 2 at a time?
(a) 40,320
(b) 720
(c) 56
(d) 28
(e) 24
17. Fig. Test 2-2 shows the results of a hypothetical experiment with eight possible outcomes, called A through H. This illustration is an example of
(a) a vertical bar graph
(b) a point-to-point graph
(c) a horizontal bar graph
(d) a histogram
(e) linear interpolation
18. In Fig. Test 2-2, the vertical, dashed line passes through a point corresponding to
(a) the mean
(b) the median
(c) the mode
(d) the distribution factor
(e) the deviation
19. What, if anything, is wrong with the graph of Fig. Test 2-2?
(a) If the frequency values of the points are added up, the sum should be equal to 100, but it obviously isn’t.
(b) A set of events with outcomes like this cannot possibly occur.
(c) The highest frequency value should be in the middle, and the values to either side should decrease steadily.
(d) The frequency values should increase steadily as you move toward the right in the graph.
(e) There is nothing wrong with this graph.
20. What is the solution to the equation 3x + 4y = 12?
(a) 3
(b) 4
(c) –3
(d) –4
(e) There is no unique solution to this equation.
21. The equation 3x2 + 5x + 3 = 0 is an example of
(a) a linear equation
(b) a quadratic equation
(c) a cubic equation
(d) a quartic equation
(e) a multivariable equation
22. In statistics, a discrete variable
(a) can attain specific, defined values
(b) can attain infinitely many values within a defined span
(c) can attain only positive-integer values
(d) can attain only non-negative integer values
(e) can never have a value greater than 1
23. Fill in the blank to make the following sentence true: “In a statistical distribution having discrete values for the independent variable, the highest cumulative absolute frequency number should be equal to the __________ of all the individual absolute frequency numbers.”
(a) average
(b) sum
(c) factorial
(d) product
(e) largest
24. In the equation 4x3 + 8x2 – 17x – 6 = 0, the numbers 4, 8, –17, and –6 are called the
(a) factors
(b) solutions
(c) coefficients
(e) imaginary numbers
25. If two outcomes H1 and H2 are complementary, then the probability, expressed as a percentage, of one outcome is equal to
(a) the probability of the other outcome
(b) 100% plus the probability of the other outcome
(c) 100% minus the probability of the other outcome
(d) 100% times the probability of the other outcome
(e) 100% divided by the probability of the other outcome
26. What can be said about the equation (x – 3)(x + 2)(x + 6) = 0?
(a) It is a linear equation.
(b) It is a quadratic equation.
(c) It is a cubic equation.
(d) It is a quartic equation.
(e) None of the above.
27. Consider the equation (x – 3)(x + 2)(x + 6) = 0. By examining this, it is apparent that
(a) there are no real-number solutions
(b) there exists exactly one real-number solution
(c) there exist exactly two different real-number solutions
(d) there exist exactly three different real-number solutions
(e) there exist infinitely many different real-number solutions
28. Suppose the two lines graphed in Fig. Test 2-3 represent linear equations. It appears that for the equation of line A, when y = 0, the value of x
(a) is not defined
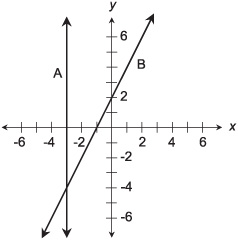
Fig. Test 2-3. Illustration for Part Two Test Questions 28 through 31.
(c) is negative
(d) can be any real number
(e) requires more information to be defined
29. Suppose the two lines graphed in Fig. Test 2-3 represent linear equations. It appears that for the equation of line A, when y is positive, the value of x
(a) is not defined
(b) is positive
(c) is negative
(d) can be any real number
(e) requires more information to be defined
30. Suppose the two lines graphed in Fig. Test 2-3 represent linear equations. It appears that for the equation of line B, when x > –1, the value of y
(a) is not defined
(b) is positive
(c) is negative
(d) can be any real number
(e) requires more information to be defined
31. Suppose the two lines graphed in Fig. Test 2-3 represent linear equations. It appears that the two equations, considered simultaneously:
(a) have no solutions
(b) have a single solution
(c) have two solutions
(d) have infinitely many solutions
(e) requires more information to be defined
32. The term fuzzy truth is used to describe
(a) a theory in which there are degrees of truth that span a range
(b) standard deviation
(c) cumulative frequency
(d) the probability fallacy
(e) any continuous distribution
33. What is the solution set of the equation x2 – 12x = –35?
(a) {12, 35}
(b) {–12, –35}
(c) {1, –12, –35}
(e) None of the above.
34. The mean for a discrete variable in a distribution is
(a) the mathematical average of the values
(b) the middle value
(c) half of the sum of the values
(d) the square root of the product of all the values
(e) the reciprocal of the sum of the values
35. In statistics, the frequency of an outcome is
(a) the number of cycles per second during which the outcome occurs
(b) the likelihood that an outcome will occur more than once
(c) an outcome chosen at random
(d) the number of times the outcome occurs within a sample
(e) an undefined term
36. What is the solution set of the equation (x – 4)2 = 0?
(a) {4}
(b) {–4}
(c) {4, –4}
(d) Ø
(e) It is impossible to tell because this equation is not in standard or factored form.
37. Consider the following pair of equations, in which the intent is to find a solution or solutions, if any, for x and y simultaneously:
3x – 4y = 8
6x + 2y = –4
This is an example of a set of
(a) two-by-two linear equations
(b) two-by-two quadratic equations
(c) cubic equations
(d) nonlinear equations
(e) redundant equations
38. In Fig. Test 2-4, suppose that curves A and B represent equations for y versus x. How many solutions are there to both equations considered simultaneously?
(a) None.
(b) One.
(c) More than one.
Fig. Test 2-4. Illustration for Part Two Test Questions 38 through 40.
(d) Infinitely many.
(e) More information is needed to answer this question.
39. In Fig. Test 2-4, suppose curve A represents the equation x + y = 0, while curve B represents the equation x4 – 2y = 0. Which of the following ordered pairs, representing values (x,y), is a solution to both of these equations considered simultaneously?
(a) (0,0)
(b) (–1,1)
(c) (1,1)
(d) (2,4)
(e) None of the above.
40. In Fig. Test 2-4, suppose that curves A and B represent equations for y versus x. What can be said in general about these equations?
(a) Neither of them is linear.
(b) One of them is linear.
(c) Both of them are linear.
(d) Both of them are quadratic.
(e) Both of them are quartic.