Solid geometry involves points, lines, and planes. The difference between two-dimensional (2D) geometry and three-dimensional (3D) geometry is the fact that, well, there’s an extra dimension! This makes things more interesting, and also more complicated.
A point can be envisioned as an infinitely tiny sphere, having height, width, and depth all equal to zero, but nevertheless possessing a specific location. A point is zero-dimensional (0D). A line can be thought of as an infinitely thin, perfectly straight, infinitely long thread or wire. It is one-dimensional (1D). A plane can be imagined as an infinitely thin, perfectly flat surface having an infinite expanse. It is two-dimensional (2D). Space in the simplest sense is the set of points representing all possible physical locations in the universe at any specific instant in time. Space is three-dimensional (3D).
If time is included in a concept of space, we get four-dimensional (4D) space, also known as hyperspace.
Points, lines, and planes in solid geometry are usually named using uppercase, italicized letters of the alphabet, just as they are in plane geometry. A common name for a point is P (for “point”). A common name for a line is L (for “line”). When it comes to planes in 3D space, we must use our imaginations. The letters X, Y, and Z are good choices. Sometimes lowercase, non-italic letters are used, such as m and n.
When we have two or more points, the letters immediately following P are used, for example Q, R, and S. If two or more lines exist, the letters immediately following L are used, for example M and N. Alternatively, numeric subscripts can be used. We might have points called P1, P2, P3, and so forth, lines called L1, L2, L3, and so forth, and planes called X1, X2, X3, and so forth.
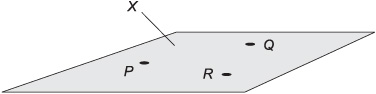
Suppose that P, Q, and R are three different geometric points, no two of which lie on the same line. Then these points define one and only one (a unique or specific) plane X. The following two statements are always true, as shown in Fig. 10-1:
• P, Q, and R lie in a common plane X.
• X is the only plane in which all three points lie.
In order to show that a surface extends infinitely in 2D, we have to be imaginative. It’s not as easy as showing that a line extends infinitely in 1D, because there aren’t any good ways to draw arrows on the edges of a plane region the way we can draw them on the ends of a line segment.

Fig 10-1. Three points P, Q, and R, not all on the same line, define a specific plane X. The plane extends infinitely in 2D.
It is customary to draw planes as rectangles in perspective; they appear as rectangles, parallelograms, or trapezoids when rendered on a flat page. This is all right, as long as it is understood that the surface extends infinitely in 2D.
Suppose that lines L and M intersect in a point P. Then the two lines define a unique plane X. The following two statements are always true, as shown in Fig. 10-2:
• L and M lie in a common plane X.
• X is the only plane in which both lines lie.
Let L be a line and P be a point not on that line. Then line L and point P define a unique plane X. The following two statements arealways true:
• L and P lie in a common plane X.
• X is the only plane in which both L and P lie.
The 2D counterpart of the 1D line segment is the simple plane region. A simple plane region consists of all the points inside a polygon or enclosed curve. The polygon or curve itself might be included in the set of points comprising the simple plane region, but this is not necessarily the case. If the polygon or curve is included, the simple plane region is said to be closed. Some examples are denoted in Fig. 10-3A; the boundaries are drawn so they look continuous. If the polygon or curve is not included, the simple plane
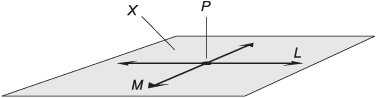
Fig 10-2. Two lines L and M, intersecting at point P, define a specific plane X. The plane extends infinitely in 2D.
Fig 10-3. Plane regions. At A, closed; at B, open.
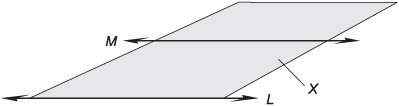
Fig 10-4. A half plane X, defined by two parallel lines, L and M. The half plane extends infinitely in 2D on the “M” side of L.
region is said to be open. In Fig. 10-3B, several examples of open simple plane regions are denoted; the boundaries are dashed.
The respective regions in Figs. 10-3A and B have identical shapes. They also have identical perimeters and identical interior areas. The outer boundaries do not add anything to the perimeter or the interior area.
These examples show specialized cases, in which the regions are contiguous, or “all of a piece,” and the boundaries are either closed all the way around or open all the way around. Some plane regions have boundaries that are closed part of the way around, or in segments; it is also possible to have plane regions composed of two or more non-contiguous subregions.
Sometimes, it is useful to talk about the portion of a geometric plane that lies “on one side” of a certain line. In Fig. 10-4, imagine the union of all possible geometric rays that start at L, then pass through line M (which is parallel to L), and extend onward past M “forever” in one direction. The region thus defined is known as a half plane.
The half plane defined by L and M might include the end line L, in which case it is closed-ended. In this case, line L is drawn as a solid line, as shown in Fig. 10-4. But the end line might not comprise part of the half plane, in which case the half plane is open-ended. Then line L is drawn as a dashed line.
Fig. 10-5. The intersection of two planes X and Y determines a unique line L. The planes extend infinitely in 2D.
Suppose that two different planes X and Y intersect; that is, they have points in common. Then the two planes intersect in a unique line L. The following two statements are always true, as shown in Fig. 10-5:
• Planes X and Y share a common line L.
• L is the only line that planes X and Y have in common.
By definition, two different lines L and M in three-space are parallel lines if and only if both of the following are true:
• Lines L and M do not intersect.
• Lines L and M lie in the same plane X.
If two lines are parallel and they lie in a given plane X, then X is the only plane in which the two lines lie. Thus, two parallel lines define a unique plane in Euclidean space.
By definition, two lines L and M in three-space are skew lines if and only if both of the following are true:
• Lines L and M do not intersect.
• Lines L and M do not lie in the same plane.
Imagine an infinitely long, straight, two-lane highway and an infinitely long, straight power line propped up on utility poles. Further imagine that the power line and the highway center line are both infinitely thin, and that the power line doesn’t sag between the poles. Suppose the power line passes over the highway somewhere. Then the center line of the highway and the power line define skew lines.
Find an example of a theoretical plane region with a finite, nonzero area but an infinite perimeter.
Examine Fig. 10-6. Suppose the three lines PQ, RS, and TU (none of which are part of the plane region X, but are shown only for reference) are mutually parallel, and that the distances d1, d2, d3,. . . are such that d2 = d1/2, d3 = d2/2, and in general, for any positive integer n, d(n+1) = dn/2. Also suppose that the length of line segment PV is greater than the length of line segment PT. Then plane region X has an infinite number of sides, each of which has a length greater than the length of line segment PT, so its perimeter is infinite. But the interior area of X is finite and nonzero, because it is obviously less than the interior area of quadrilateral PQSR but greater than the area of quadrilateral TUSR.
How many planes can mutually intersect in a given line L?
In theory, an infinite number of planes can all intersect in a common line. Think of the line as an infinitely long hinge, and then imagine a plane that can swing around this hinge. Each position of the swinging plane represents a unique plane in space.
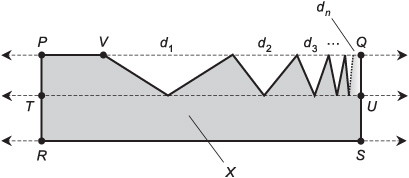
Fig 10-6. Illustration for Problem 10-1.
In Euclidean three-space, geometric solids with straight edges have flat faces, also called facets, each of which forms a plane polygon. An object of this sort is known as a polyhedron.
A polyhedron in 3D must have at least four faces. A four-faced polyhedron is called a tetrahedron. Each of the four faces of a tetrahedron is a triangle. There are four vertices. Any four specific points, not all in a single plane, form a unique tetrahedron.
Figure 10-7 shows a tetrahedron. The surface area is found by adding up the interior areas of all four triangular faces. In the case of a regular tetrahedron, all six edges have the same length, and therefore all four faces are equilateral triangles. If the length of each edge of a regular tetrahedron is equal to s units, then the surface area, B, of the whole four-faced regular tetrahedron is given by:
B = 31/2 s2
In this formula, 31/2 represents the square root of 3, or approximately 1.732.
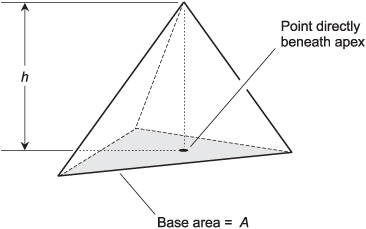
Fig 10-7. A tetrahedron has four faces (including the base) and six edges.
Imagine a tetrahedron whose base is a triangle with area A, and whose height is h as shown in Fig. 10-7. The volume, V, of the figure is given by:
V = Ah/3
Figure 10-8 illustrates a pyramid. This figure has a square or rectangular base and four slanted faces. If the base is a square, and if the apex (the top of the pyramid) lies directly above a point at the center of the base, then the figure is a regular pyramid, and all of the slanted faces are isosceles triangles.
The surface area of a pyramid is found by adding up the areas of all five of its faces (the four slanted faces plus the base). In the case of a regular pyramid where the length of each slanted edge, called the slant height, is equal to s units and the length of each edge of the base is equal to t units, the surface area, B, is given by:
B = t2 + 2 t(s2 − t2/4)1/2
In the case of an irregular pyramid, the problem of finding the surface area is more complicated, because it involves individually calculating the area of the base and each slanted face, and then adding all the areas up.
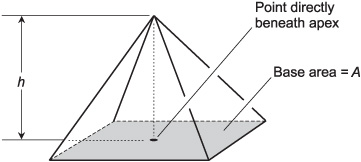
Fig 10-8. A pyramid has five faces (including the base) and eight edges.
Imagine a pyramid whose base is a square with area A, and whose height is h as shown in Fig. 10-8. The volume, V, of the pyramid is given by:
V = Ah/3
This is true whether the pyramid is regular or irregular.
Figure 10-9 illustrates a cube. This is a regular hexahedron (six-sided polyhedron). It has 12 edges, each of which is of the same length, and eight vertices. Each of the six faces is a square.
Imagine a cube whose edges each have length s, as shown in Fig. 10-9. The surface area, A, of the cube is given by:
A = 6s2
Imagine a cube as defined above and in Fig. 10-9. The volume, V, of the solid enclosed by the cube is given by:
V = s3
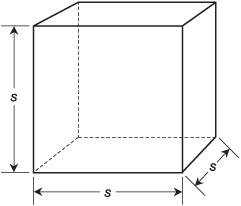
Fig 10-9. A cube has six square faces and 12 edges of identical length.
Fig. 10-10. A rectangular prism has six rectangular faces and 12 edges.
Figure 10-10 illustrates a rectangular prism. This is a hexahedron, each of whose six faces is a rectangle. The figure has 12 edges and eight vertices.
Imagine a rectangular prism whose edges have lengths s1, s2, and s3 as shown in Fig. 10-10. The surface area, A, of the prism is given by:
A = 2s1s2 + 2s1s3 + 2s2s3
Imagine a rectangular prism as defined above and in Fig. 10-10. The volume, V, of the enclosed solid is given by:
V = s1s2s3
A parallelepiped is a six-faced polyhedron in which each face is a parallelogram, and opposite pairs of faces are congruent. The figure has 12 edges and eight vertices. The acute angles between the pairs of edges are x, y, and z, as shown in Fig. 10-11.
Imagine a parallelepiped with faces of lengths s1, s2, and s3. Suppose the angles between pairs of edges are x, y, and z as shown in Fig. 10-11.
Fig 10-11. A parallelepiped has six faces, all of which are parallelograms, and 12 edges.
The surface area, A, of the parallelepiped is given by:
A = 2s1s2 sin x + 2s1s3 sin y + 2s2s3 sin z
where sin x represents the sine of angle x, sin y represents the sine of angle y, and sin z represents the sine of angle z. Sines of angles can be found with any scientific calculator, including the ones in most personal computers.
Imagine a parallelepiped whose faces have lengths s1, s2, and s3, and that has angles between edges of x, y, and z as shown in Fig. 10-11. Suppose further that the height of the parallelepiped, as measured along a line normal to the base, is equal to h. The volume, V, of the enclosed solid is equal to the product of the base area and the height:
V = hs1s3 sin y
Suppose you want to paint the interior walls of a room in a house. The room is shaped like a rectangular prism. The ceiling is exactly 3.0 m above the floor. The floor and the ceiling both measure exactly 4.2m by 5.5 m. There are two windows, the outer frames of which both measure 1.5 m high by 1.0 m wide. There is one doorway, the outer frame of which measures 2.5 m high by 1.0 m wide. With two coats of paint (which you intend to apply), one liter of paint can be expected to cover exactly 20 m2 of wall area. How much paint, in liters, will you need to completely do the job? Note that a liter is defined as a cubic decimeter, or the volume of a cube measuring 0.1 meter on an edge. This means that a liter is equal to 0.001 cubic meter (m3).
It is necessary to find the amount of wall area that this room has. Based on the information given, we can conclude that the rectangular prism formed by the edges between walls, floor, and ceiling measures 3.0 m high by 4.2m wide by 5.5m deep. So we can let s1 = 3.0, s2 = 4.2, and s3 = 5.5 (with all units assumed to be in meters) to find the surface area A of the rectangular prism, in square meters, neglecting the area subtracted for the windows and doorway. Using the formula:
A = 2s1s2 + 2s1s 3 + 2s2s3
= (2 × 3.0 × 4.2) + (2 × 3.0 × 5.5) + (2 × 4.2 × 5.5)
= 25.2 + 33.0 + 46.2
= 104.4m2
There are two windows measuring 1.5 m by 1.0 m. Each window takes away 1.5 × 1.0 = 1.5m2 of area. The doorway measures 2.5 m by 1.0 m, so it takes away 2.5 × 1.0 = 2.5 m2. Therefore, the windows and doorway combined take away 1.5 + 1.5 + 2.5 = 5.5 m2 of wall space. We must also take away the areas of the floor and ceiling. This is the final factor in the above equation, 2s2s3 = 46.2. The wall area to be painted, call it Aw, is calculated this way:
Aw = (104.4 − 5.5) − 46.2
= 52.7 m2
A liter of paint can be expected to cover 20 m2. So we will need 52.7/20, or 2.635, liters of paint to do this job.
A cone has a circular or elliptical base and an apex point. The cone itself consists of the union of the following sets of points:
• The circle or ellipse.
• All points inside the circle or ellipse and that lie in its plane.
• All line segments connecting the circle or ellipse (not including its interior) and the apex point.
The interior of the cone consists of the set of all points within the cone. The surface might or might not be included in the definition of the interior.
A cylinder has a circular or elliptical base, and a circular or elliptical top that is congruent to the base and that lies in a plane parallel to the base. The cylinder itself consists of the union of the following sets of points:
• The base circle or ellipse.
• All points inside the base circle or ellipse and that lie in its plane.
• The top circle or ellipse.
• All points inside the top circle or ellipse and that lie in its plane.
• All line segments connecting corresponding points on the base circle or ellipse and top circle or ellipse (not including their interiors).
The interior of the cylinder consists of the set of all points within the cylinder. The surface might or might not be included in the definition of the interior.
These are general definitions, and they encompass a great variety of objects! Here, we’ll look only at cones and cylinders whose bases are circles.
A right circular cone has a base that is a circle, and an apex point on a line perpendicular to the base and passing through its center. This type of cone, when the height is about twice the diameter of the base, has a “dunce cap” shape. Dry sand, when poured into an enormous pile on a flat surface, acquires a shape that is roughly that of a right circular cone. An example of this type of object is shown in Fig. 10-12.
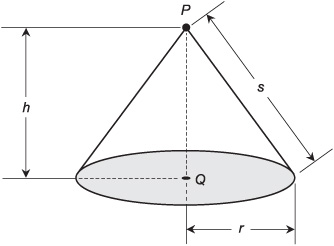
Fig 10-12. A right circular cone.
Imagine a right circular cone as shown in Fig. 10-12. Let P be the apex of the cone, and let Q be the center of the base. Let r be the radius of the base, let h be the height of the cone (the length of line segment PQ), and let s be the slant height of the cone as measured from any point on the edge of the base to the apex P. The surface area S1 of the cone, including the base, is given by either of the following formulas:
S1 = πr2 + πrs
S1 = πr2 + πr(r2 + h2)1/2
The surface area S2 of the cone, not including the base, is called the lateral surface area and is given by either of the following:
S2 = πrs
S2 = πr(r2 + h2)1/2
Imagine a right circular cone as defined above and in Fig. 10-12. The volume, V, of the interior of the figure is given by:
V = πr2h/3
A slant circular cone has a base that is a circle, just as does the right circular cone. But the apex is such that a line, perpendicular to the plane containing the base and running from the apex through the plane containing the base, does not pass through the center of the base. Such a cone has a “blown-over” or “cantilevered” appearance (Fig. 10-13).
Imagine a cone whose base is a circle. Let P be the apex of the cone, and let Q be a point in the plane X containing the base such that line segment PQ is perpendicular to X (Fig. 10-13). Let h be the height of the cone (the length
Fig 10-13. A slant circular cone.
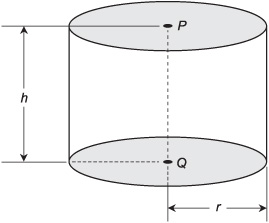
Fig 10-14. A right circular cylinder.
of line segment PQ). Let r be the radius of the base. Then the volume, V, of the corresponding cone is given by:
V = πr2h/3
This is the same as the formula for the volume of a right circular cone.
A right circular cylinder has a circular base and a circular top. The base and the top lie in parallel planes. The center of the base and the center of the top lie along a line that is perpendicular to both the plane containing the base and the plane containing the top. A general example is shown in Fig. 10-14.
Imagine a right circular cylinder where P is the center of the top and Q is the center of the base (Fig. 10-14). Let r be the radius of the cylinder, and let h be the height (the length of line segment PQ). Then the surface area S1 of the cylinder, including the base, is given by:
S1 = 2πrh + 2πr2 = 2πr (h + r)
The lateral surface area S2 of the cylinder (not including the base) is given by:
S2 = 2 πrh
Imagine a right circular cylinder as defined above and shown in Fig. 10-14. The volume, V, of the cylinder is given by:
V = πr2h
A slant circular cylinder has a circular base and a circular top. The base and the top lie in parallel planes. The center of the base and the center of the top lie along a line that is not perpendicular to the planes that contain them (Fig. 10-15).
Imagine a slant circular cylinder as defined above and in Fig. 10-15. The volume, V, of the corresponding solid is given by:
V = πr2h
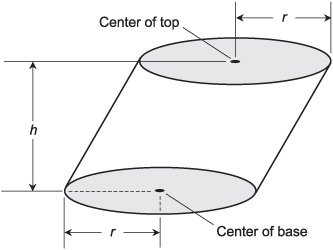
Fig. 10-15. A slant circular cylinder.
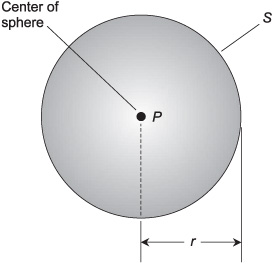
Consider a specific point P in 3D space. The surface of a sphere S consists of the set of all points at a specific distance or radius r from point P. The interior of sphere S, including the surface, consists of the set of all points whose distance from point P is less than or equal to r. The interior of sphere S, not including the surface, consists of the set of all points whose distance from P is less than r.
Imagine a sphere S having radius r as shown in Fig. 10-16. The surface area, A, of the sphere is given by:
A = 4πr2
Imagine a sphere S as defined above and in Fig. 10-16. The volume, V, of the solid enclosed by the sphere is given by:
V = 4πr3/3
This volume applies to the interior of sphere S, either including the surface or not including it, because the surface has zero volume.
A cylindrical water tower is exactly 30 m high and exactly 10 m in radius. How many liters of water can it hold, assuming the entire interior can be filled with water? Round the answer off to the nearest liter.
Use the formula for the volume of a right circular cylinder to find the volume in cubic meters:
V = πr2h
Plug in the numbers. Let r = 10, h = 30, and π = 3.14159:
V = 3.14159 × 102 × 30
= 3.14159 × 100 × 30
= 9424.77 m3
There are 1000 liters per cubic meter. This means that the amount of water the tower can hold, in liters, is equal to 9424.77 × 1000, or 9,424,770.
A circus tent is shaped like a right circular cone. Its diameter is 50 m and the height at the center is 20 m. How much canvas is in the tent? Express the answer to the nearest square meter.
Use the formula for the lateral surface area, S, of the right circular cone:
S = πr(r2 + h2)1/2
We know that the diameter is 50 m, so the radius is 25 m. Therefore, r = 25. We also know that h = 20. Let π = 3.14159. Then:
S = 3.14159 × 25 ×(252 + 202)1/2
= 3.14159 × 25 ×(625 + 400)1/2
= 3.14159 × 25 × 10251/2
= 3.14159 × 25 × 32.0156
= 2514.4972201m2
There are 2514m2 of canvas, rounded off to the nearest square meter.
Suppose a football field is to be covered by an inflatable dome that takes the shape of a half-sphere. If the radius of the dome is 100 m, what is the volume of air enclosed by the dome, in cubic meters? Find the result to the nearest 1000m3.
First, we must find the volume V of a sphere whose radius is 100 m, and then divide the result by 2. Let π = 3.14159. Using the formula with r = 100 gives this result:
V = (4 × 3.14159 × 1003)/3
= (4 × 3.14159 × 1,000,000)/3
= 4,188,786.667 m3
Thus V/2 = 4,188,786.667/2 = 2,094,393.333 m3. Rounding off to the nearest 1000 m3, we obtain the figure of 2,094,000 m3 as the volume of air enclosed by the dome.
Refer to the text in this chapter if necessary. A good score is eight correct. Answers are in the back of the book.
1. What is the approximate surface area of the sides (not including the base or top) of a water tower that is shaped like a right circular cylinder, that has a radius of exactly 5 meters, and that is exactly 20 meters tall?
(a) 1571m2
(b) 628.3m2
(c) 100 m2
(d) It cannot be determined without more information.
2. If the height of a silo that is shaped like a right circular cylinder is cut in half while its radius remains the same, what happens to its surface area (not including the base or the top)?
(a) It decreases to 1/2 of its previous value.
(b) It decreases to 1/4 of its previous value.
(c) It decreases to 1/8 of its previous value.
(d) It decreases to 1/16 of its previous value.
3. If the height of a silo that is shaped like a right circular cylinder is cut in half while its radius remains the same, what happens to its volume?
(a) It decreases to 1/2 of its previous value.
(b) It decreases to 1/4 of its previous value.
(c) It decreases to 1/8 of its previous value.
(d) It decreases to 1/16 of its previous value.
4. What is the approximate volume, in cubic centimeters (cm3), of a ball that is exactly 20 cm in diameter? (Remember that the diameter of a sphere is twice the radius.)
(a) 62.83 cm3
(b) 1257 cm3
(c) 4189 cm3
(d) It cannot be determined without more information.
5. Which of the following statements is not true in Euclidean 3D space?
(a) If two straight lines are parallel, then they are skew.
(b) If two straight lines are parallel, then they lie in the same plane.
(c) If two straight lines are parallel, then they determine a unique plane.
(d) If two straight lines are parallel, then they do not intersect.
6. Which of the following statements is always true in Euclidean 3D space?
(a) Four points determine a unique flat plane.
(b) Three points can have more than one flat plane in common.
(c) Two lines that do not intersect determine a unique flat plane.
(d) None of the statements (a), (b), or (c) is always true in Euclidean 3D space.
7. If the radius of a sphere increases by a factor of 10, the volume of the sphere increases by a factor of
(a) 100
(b) (400/3)π
(c) 1000
(d) (4000/3)π
8. The boundary of a closed plane region
(a) adds nothing to its area
(b) increases its volume
(c) reduces its perimeter
(d) is always a straight line
9. A cube is a special form of
(a) rhombus
(b) pyramid
(c) cone
(d) parallelepiped
10. If the radius of a sphere increases by a factor of 9, the ratio of the volume of the sphere to its surface area increases by a factor of
(a) 3
(b) 9
(c) 27
(d) 81