Trigonometry (or “trig”) involves angles and distances. Trigonometry scares some people because of the Greek symbology, but the rules are clear-cut. Once you can get used to the idea of Greek letters representing angles, and if you’re willing to draw diagrams and use a calculator, basic trigonometry loses most of its fear-inspiring qualities. You might even find yourself having fun with it.
Circles are defined by equations in which either x or y can be considered the dependent variable. We’ve already looked at the graphs of some simple circles in the xy-plane. Let’s look more closely at this special species of geometric figure.
The equation in the xy-plane that represents a circle depends on two things: the radius of the circle, and the location of its center point.
Suppose r is the radius of a circle, expressed in arbitrary units. Imagine that the center point of the circle in Cartesian coordinates is located at the point x = a and y = b, represented by the ordered pair (a, b). Then the equation of that circle is:
(x – a)2 + (y – b)2 = r2
If the center of the circle happens to be at the origin, that is, at (0,0) on the coordinate plane, then the general equation is simpler:
x2 + y2 = r2
Consider a circle in rectangular coordinates with the following equation:
x2 + y2 = 1
This is called the unit circle because its radius is 1 unit, and it is centered at the origin (0,0). This circle gives us a good way to define the common trigonometric functions, which are sometimes called circular functions.
In trigonometry, mathematicians and scientists have acquired the habit of using Greek letters to represent angles. The most common symbol for this purpose is an italic, lowercase Greek theta (pronounced “THAY-tuh”). It looks like an italic numeral 0 with a horizontal line through it (θ).
When writing about two different angles, a second Greek letter is used along with θ. Most often, it is the italic, lowercase letter phi (pronounced “FIE” or “FEE”). This character looks like an italic lowercase English letter o with a forward slash through it (Φ).
Sometimes the italic, lowercase Greek alpha (“AL-fuh”), beta (“BAY-tuh”), and gamma (“GAM-uh”) are used to represent angles. These, respectively, look like this: α, β, γ. When things get messy and there are a lot of angles to talk about, numeric subscripts are sometimes used with Greek letters, so don’t be surprised if you see text in which angles are denoted θ1, θ2, θ3, and so on.
There are two main units by which the measures of angles in a flat plane can be specified: the radian and the degree. The radian was defined in the previous chapter. A quarter circle is π/2 rad, a half circle is π rad, and three quarters of a circle is 3π/2 rad. Mathematicians prefer to use the radian when working with trigonometric functions, and the abbreviation “rad” is left out. So if you see something like θ1 = π/4, you know the angle θ1 is expressed in radians.
The angular degree (°), also called the degree of arc, is the unit of angular measure most familiar to lay people. One degree (1°) is 1/360 of a full circle. An angle of 90° represents a quarter circle, 180° represents a half circle, 270° represents three quarters of a circle, and 360° represents a full circle. A right angle has a measure of 90°, an acute angle has a measure of more than 0° but less than 90°, and an obtuse angle has a measure of more than 90° but less than 180°.
To denote the measures of tiny angles, or to precisely denote the measures of angles in general, smaller units are used. One minute of arc or arc minute, symbolized by an apostrophe or accent (′) or abbreviated as m or min, is 1/60 of a degree. One second of arc or arc second, symbolized by a closing quotation mark (″) or abbreviated as s or sec, is 1/60 of an arc minute or 1/3600 of a degree. An example of an angle in this notation is 30° 15′ 0″, which is read as “30degrees, 15minutes, 0seconds.”
Alternatively, fractions of a degree can be denoted in decimal form. You might see, for example, 30.25°. This is the same as 30° 15′ 0″. Decimal fractions of degrees are easier to work with than the minute/second scheme when angles must be added and subtracted, or when using a conventional calculator to work out trigonometry problems. Nevertheless, the minute/second system, like the English system of measurements, remains in widespread use.
A text discussion tells you that θ1 = π/4. What is the measure of θ1 in degrees?
There are 2π rad in a full circle of 360°. The value π/4 is equal to 1/8 of 2π. Therefore, the angle θ1 is 1/8 of a full circle, or 45°.
Suppose your town is listed in an almanac as being at 40° 20′ north latitude and 93° 48′ west longitude. What are these values in decimal form? Express your answers to two decimal places.
There are 60 minutes of arc in one degree. To calculate the latitude, note that 20′ = (20/60)° = 0.33°; that means the latitude is 40.33° north. To calculate the longitude, note that 48′ = (48/60)° = 0.80°; that means the longitude is 93.80° west.
Consider a circle in the Cartesian xy-plane with the following equation:
x2 + y2 = 1
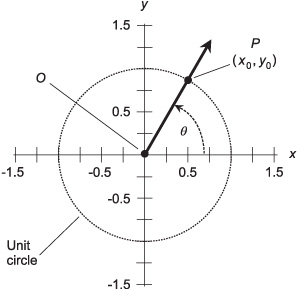
This equation, as defined earlier in this chapter, represents the unit circle. Let θ be an angle whose apex is at the origin, and that is measured counterclockwise from the x axis, as shown in Fig. 12-1. Suppose this angle corresponds to a ray that intersects the unit circle at some point P = (x0, y0). We can define the three basic circular functions, also called the primary circular functions, of the angle θ in an elegant way. But before we get into this, let’s extend our notion of angles to cover negative values, and also to cover values more than 360° (2π rad).
In trigonometry, any direction angle expressible as a real number, no matter how extreme, can always be reduced to something that is at least 0° (0 rad)

Fig. 12-1. The unit circle is the basis for the trigonometric functions.
but less than 360° (2π rad). If you look at Fig. 12-1, you should be able to envision how this works. Even if the ray OP makes more than one complete revolution counterclockwise from the x axis, or if it turns clockwise instead, its direction can always be defined by some counterclockwise angle of least 0° (0 rad) but less than 360° (2π rad) relative to the x axis.
Any offbeat direction angle such as 730° or –9π/4 rad can be reduced to a direction angle that measures at least 0° (0 rad) but less than 360° (2π rad) by adding or subtracting some whole-number multiple of 360° (2π rad). But you have to be careful about this. A direction angle specifies orientation only. The orientation of the ray OP is the same for an angle of 540° (3π rad) as for an angle of 180° (π rad), but the larger value carries with it the insinuation that the ray (also called a vector) OP has revolved 1.5 times around, while the smaller angle implies that it has undergone less than one complete revolution. Sometimes this doesn’t matter, but often it does!
Negative angles are encountered in trigonometry, especially in graphs of functions. Multiple revolutions of objects are important in physics and engineering. So if you ever hear or read about an angle such as –90°, –π/2 rad, 900°, or 5π rad, you can be confident that it has meaning. The negative value indicates clockwise rotation. An angle that is said to measure more than 360° (2π rad) indicates more than one complete revolution counterclockwise. An angle that is said to measure less than –360° (–2π rad) indicates more than one revolution clockwise.
In Fig. 12-1, imagine ray OP pointing along the x axis, and then starting to rotate counterclockwise on its end point O, as if point O is a mechanical bearing. The point P, represented by coordinates (x0, y0), thus revolves around point O, following the perimeter of the unit circle.
Imagine what happens to the value of y0 (the ordinate of point P) during one complete revolution of ray OP. The ordinate of P starts out at y0 = 0, then increases until it reaches y0 = 1 after P has gone 90° or π/2 rad around the circle (θ = 90° = π/2). After that, y0 begins to decrease, getting back to y0 = 0 when P has gone 180° or π rad around the circle (θ = 180° = π). As P continues on its counterclockwise trek, y0 keeps decreasing until, at θ = 270° = 3π/2, the value of y0 reaches its minimum of –1. After that, the value of y0 rises again until, when P has gone completely around the circle, it returns to y0 = 0 for θ = 360° = 2π.
The value of y0 is defined as the sine of the angle θ. The sine function is abbreviated sin, so we can state this simple equation:
sin θ = y0
Imagine that you attach a “glow-in-the-dark” ball to the end of a string, and then swing the ball around and around at a rate of one revolution per second. The ball describes a circle as viewed from high above, as shown in Fig. 12-2A. Suppose you make the ball circle your head so the path of the ball lies in a perfectly horizontal plane. Imagine that you are in the middle of a flat, open field on a perfectly dark night. If a friend stands far away with his or her eyes exactly in the plane of the ball’s orbit and looks at you and the ball through a pair of binoculars, what does your friend see?
Your friend, watching from a great distance and from a viewpoint exactly in the plane defined by the ball’s orbit, sees a point of light that oscillates back and forth, from right-to-left and left-to-right, along what appears to be a straight-line path (Fig. 12-2B). Starting from its extreme right-most apparent position, the glowing point moves toward the left for half a second, speeding up and then slowing down; then it stops and reverses direction; then it moves toward the right for half a second, speeding up and then slowing down; then it stops and turns around again. This goes on and on for as long as you care to swing the ball around your head. As seen by your friend, the ball reaches its extreme right-most position at one-second intervals because its orbital speed is one revolution per second.
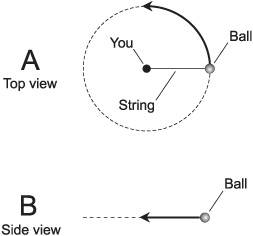
Fig. 12-2. Orbiting ball and string. At A, as seen from above; at B, as seen edge-on.
If you graph the apparent position of the ball as seen by your friend with respect to time, the result is a sine wave, which is a graphical plot of a sine function. Some sine waves “rise higher and lower” (corresponding to a longer string), some are “flatter” (a shorter string), some are “stretched out” (a slower rate of revolution), and some are “squashed” (a faster rate of revolution). But the characteristic shape of the wave, known as a sinusoid, is the same in every case.
You can whirl the ball around faster or slower than one revolution per second. The string can be made longer or shorter. These adjustments alter the frequency and/or the amplitude of the sine wave. But any sinusoid can be defined as the path of a point that orbits a central point in a perfect circle, with a certain radius, at a certain rate of revolution.
Circular motion in the Cartesian plane can be defined in terms of a general formula:
y = a sin bθ
where a is a constant that depends on the radius of the circle, and b is a constant that depends on the revolution rate. The angle θ is expressed in a counterclockwise direction from the positive x axis. Figure 12-3 illustrates a graph of the basic sine function: a sine wave for which a = 1 and b = 1, and for which the angle is expressed in radians.
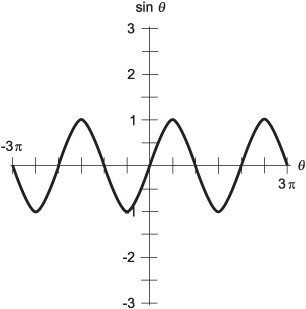
Fig. 12-3. Graph of the sine function for values of θ between –3π rad and 3π rad.
Look again at Fig. 12-1. Imagine, once again, a ray from the origin outward through point P on the circle, pointing at first along the x axis, and then rotating in a counterclockwise direction.
What happens to the value of x0 during one complete revolution of the ray? It starts out at x0 = 1, then decreases until it reaches x0 = 0 when θ = 90° = π/2. After that, x0 continues to decrease, getting down to x0 = –1 when θ = 180° = π. As P continues counterclockwise around the circle, x0 begins to increase again; at θ = 270° = 3π/2, the value gets back up to x0 = 0. After that, x0 increases further until, when P has gone completely around the circle, it returns to x0 = 1 for θ = 360° = 2π.
The value of x0 is defined as the cosine of the angle θ. The cosine function is abbreviated cos. So we can write this:
cos θ = x0
Circular motion in the Cartesian plane can be defined in terms of the cosine function as well as the sine function:
y = a cos bθ
where a is a constant that depends on the radius of the circle, and b is a constant that depends on the revolution rate, just as is the case with the sine function. The angle θ is measured or defined counterclockwise from the positive x axis, also after the fashion of the sine function.
The shape of a cosine wave is exactly the same as the shape of a sine wave. Both waves are sinusoids. But the cosine wave is shifted in phase by 1/4 cycle (90° or π/2 rad) with respect to the sine wave. Figure 12-4 illustrates a graph of the basic cosine function: a cosine wave for which a = 1 and b = 1, and for which the angle is expressed in radians.
Once again, refer to Fig. 12-1. The tangent (abbreviated tan) of an angle θ is defined using the same ray OP and the same point P = (x0, y0) as is done with the sine and cosine functions. The definition is:
tan θ = y0/x0
Fig. 12-4. Graph of the cosine function for values of θ between –3π rad and 3π rad.
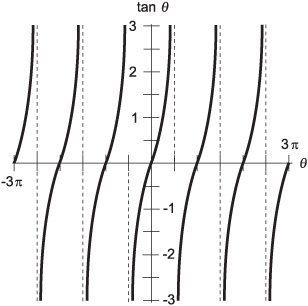
Fig. 12-5. Graph of the tangent function for values of θ between –3π rad and 3π rad.
We already know that sin θ = y0 and cos θ = x0, so we can express the tangent function in terms of the sine and the cosine:
tan θ = sin θ/cos θ
This function is interesting because, unlike the sine and cosine functions, it “blows up” at certain values of θ. This is shown by the graph of the tangent function (Fig. 12-5). Whenever x0 = 0, the denominator of either quotient above becomes zero. Division by zero is not defined, and that means the tangent function is not defined for any angle θ such that cos θ = 0. Such angles are all the positive and negative odd-integer multiples of 90° (π/2 rad).
What is tan 45°? Do not perform any calculations. You should be able to infer this without having to write down a single numeral.
Draw a diagram of a unit circle, such as the one in Fig. 12-1, and place ray OP such that it subtends an angle of 45° with respect to the x axis. That angle is the angle for which we want to find the tangent. Note that the ray OP also subtends an angle of 45° with respect to the y axis, because the x and y axes are perpendicular (they are oriented at 90° with respect to each other), and 45° is exactly half of 90°. Every point on the ray OP is equally distant from the x and y axes; this includes the point (x0, y0). It follows that x0 = y0, and neither of them is equal to zero. From this, we can conclude that y0/x0 = 1. According to the definition of the tangent function, therefore, tan 45° = 1.
The three functions defined above form the cornerstone for trigonometry. But three more circular functions exist. Their values represent the reciprocals of the values of the primary circular functions.
Imagine the ray OP in Fig. 12-1, at an angle θ with respect to the x axis, pointing outward from the origin, and intersecting the unit circle at the point P = (x0, y0). The reciprocal of the ordinate, that is, 1/y0, is defined as the cosecant of the angle θ. The cosecant function is abbreviated csc, so we can say this in mathematical terms:
csc θ = 1/y0
The cosecant function is the reciprocal of the sine function. For any angle θ, the following equation is always true as long as sin θ is
Fig. 12-6. Graph of the cosecant function for values of θ between –3π rad and 3π rad.
not equal to zero:
csc θ = 1 / sin θ
The cosecant function is not defined for 0° (0 rad), or for any multiple of 180° (π rad). This is because the sine of any such angle is equal to 0, which would mean that the cosecant would have to be 1/0. We can’t do anything with a quotient in which the denominator is 0.
Figure 12-6 is a graph of the cosecant function for values of θ between –3π and 3π. Note the angles at which the function “explodes.”
Now consider the reciprocal of the abscissa, that is, 1/x0, in Fig. 12-1. This is the secant of the angle θ. The secant function is abbreviated sec, so we can define it like this:
sec θ = 1 / x0
The secant of any angle is the reciprocal of the cosine of that angle. As long as cos θ is not equal to zero, the following is true:
sec θ = 1 / cos θ
Fig. 12-7. Graph of the secant function for values of θ between –3π rad and 3π rad.
The secant function is not defined for 90° (π/2 rad), or for any positive or negative odd multiple thereof. Figure 12-7 is a graph of the secant function for values of θ between –3π and 3π. Note the angles at which the function “blows up.”
There’s one more circular function. Consider the value of x0/y0 at the point P where the ray OP crosses the unit circle. This quotient is called the cotangent of the angle θ. The word “cotangent” is abbreviated as cot. For any ray anchored at the origin and crossing the unit circle at an angle θ:
cot θ = x0/y0
Because we already know that sin θ = y0 and cos θ = x0, we can express the cotangent function in terms of the sine and the cosine:
cot θ = cos θ / sin θ
The cotangent function is also the reciprocal of the tangent function:
cot θ = 1 / tan θ
This function, like the tangent function, “explodes” at certain values of θ. Whenever y0 = 0, the denominator of either quotient above becomes zero, and the cotangent function is not defined. This occurs at all integer multiples
Fig. 12-8. Graph of the cotangent function for values of θ between –3π rad and 3π rad.
of 180° (π rad). Figure 12-8 is a graph of the cotangent function for values of θ between –3π and 3π.
Now that you know how the circular functions are defined, you might wonder how the values are calculated. The answer: with a calculator! Most personal computers have a calculator program built into the operating system. You might have to dig around in the folders to find it, but once you do, you can put a shortcut to it on your computer’s desktop. Put the calculator in the “scientific” mode.
The values of the sine and cosine function never get smaller than –1 or larger than 1. The values of other functions can vary wildly. Put a few numbers into your calculator and see what happens when you apply the circular functions to them. Pay attention to whether you’re using degrees or radians. When the value of a function “blows up” (the denominator in the unit-circle equation defining it becomes zero), you’ll get an error message on the calculator.
Use a portable scientific calculator, or the calculator program in a personal computer, to find the values of all six circular functions of 66°. Round your answers off to three decimal places. If your calculator does not have keys for the cosecant (csc), secant (sec), or cotangent (cot) functions, first find the sine (sin), cosine (cos), and tangent (tan) respectively, then find the reciprocal, and finally round off your answer to three decimal places.
You should get the following results. Be sure your calculator is set to work with degrees, not radians.
sin 66° = 0.914
cos 66° = 0.407
tan 66° = 2.246
csc 66° = 1/(sin 66°) = 1.095
sec 66° = 1/(cos 66°) = 2.459
cot 66 = 1/(tan 66°) = 0.445
We have just defined the six circular functions – sine, cosine, tangent, cosecant, secant, and cotangent – in terms of points on a circle. There is another way to define these functions: the right-triangle model.
In geometry, it is customary to denote triangles by writing an uppercase Greek letter delta (Δ) followed by the names of the three points representing the corners, or vertices, of the triangle. For example, if P, Q, and R are the names of three points, then ΔPQR is the triangle formed by connecting these points with straight line segments. We read this as “triangle PQR.”
Angles are denoted by writing the symbol ∠(which resembles an extremely italicized, uppercase English letter L without serifs) followed by the names of three points that uniquely determine the angle. This scheme lets us specify the extent and position of the angle, and also the rotational sense in which it is expressed. For example, if there are three points P, Q, and R, then ∠PQR (read “angle PQR”) has the same measure as ∠RQP, but in the opposite direction. The middle point, Q, is the vertex of the angle.
The rotational sense in which an angle is measured can be significant in physics, astronomy, and engineering, and also when working in coordinate systems. In the Cartesian plane, remember that angles measured counterclockwise are considered positive, while angles measured clockwise are considered negative. If we have ∠PQR that measures 30° around a circle in Cartesian coordinates, then ∠RQP measures –30°, whose direction is equivalent to an angle of 330°. The cosines of these two angles happen to be the same, but the sines differ.
Consider a right triangle defined by points P, Q, and R, as shown in Fig. 12-9. Suppose that ∠QPR is a right angle, so ΔPQR is a right triangle. Let d be the length of line segment QP, e be the length of line segment PR, and f be the length of line segment QR. Let θ be ∠PQR, the angle measured counterclockwise between line segments QP and QR. The six circular trigonometric functions can be defined as ratios between the lengths of the sides, as follows:
sin θ = e/f
cos θ = d/f
tan θ = e/d
csc θ = f/e
sec θ = f/d
cot θ = d/e
The longest side of a right triangle is always opposite the 90° angle, and is called the hypotenuse. In Fig. 12-9, this is the side QR whose length is f The other two sides are called adjacent sides because they are both adjacent to the right angle.
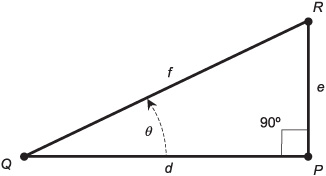
Fig. 12-9. The right-triangle model for defining trigonometric functions. All right triangles obey the theorem of Pythagoras. Illustration for Problems 12-5 and 12-6.
The following fact can be useful in deducing the measures of angles in trigonometric calculations. It’s a simple theorem in geometry that you should remember. In any triangle, the sum of the measures of the interior angles is 180° (π rad). This is true whether it is a right triangle or not, as long as all the angles are measured in the plane defined by the three vertices of the triangle.
In the right-triangle model, the values of the circular functions are defined only for angles between, but not including, 0° and 90° (0 rad and π/2 rad). All angles outside this range are better dealt with using the unit-circle model.
Using the right-triangle scheme, a trigonometric function is undefined whenever the denominator in its “side ratio” (according to the formulas above) is equal to zero. The length of the hypotenuse (side f) is never zero, but if a right triangle is “squashed” or “squeezed” flat either horizontally or vertically, then the length of one of the adjacent sides (d or e) can become zero. Such objects aren’t triangles in the strict sense, because they have only two vertices rather than three.
Suppose there is a triangle whose sides are 3, 4, and 5 units, respectively. What is the sine of the angle θ opposite the side that measures 3 units? Express your answer to three decimal places.
If we are to use the right-triangle model to solve this problem, we must first be certain that a triangle with sides of 3, 4, and 5 units is a right triangle. Otherwise, the scheme won’t work. We can test for this by seeing if the Pythagorean theorem applies. If this triangle is a right triangle, then the side measuring 5 units is the hypotenuse, and we should find that 32 + 42 = 52. Checking, we see that 32 = 9 and 42 = 16. Therefore, 32 + 42 = 9 + 16 = 25, which is equal to 52. It’s a right triangle, indeed!
It helps to draw a picture here, after the fashion of Fig. 12-9. Put the angle θ, which we are analyzing, at lower left (corresponding to the vertex point Q). Label the hypotenuse f = 5. Now we must figure out which of the other sides should be called d, and which should be called e. We want to find the sine of the angle opposite the side whose length is 3 units, and this angle, in Fig. 12-9, is opposite side PR, whose length is equal to e. So we set e = 3. That leaves us with no other choice for d than to set d = 4.
According to the formulas above, the sine of the angle in question is equal to e/f. In this case, that means sin θ = 3/5 = 0.600.
What are the values of the other five circular functions for the angle θ as defined in Problem 12-5? Express your answers to three decimal places.
Plug numbers into the formulas given above, representing the ratios of the lengths of sides in the right triangle:
cos θ = d/f = 4/5 = 0.800
tan θ = e/d = 3/4 = 0.750
csc θ = f/e = 5/3 = 1.667
sec θ = f/d = 5/4 = 1.250
cot θ = d/e = 4/3 = 1.333
The theorem of Pythagoras, which you learned earlier in this book, can be extended to cover two important facts involving the circular trigonometric functions. These are worth remembering.
The sum of the squares of the sine and cosine of an angle is always equal to 1. In mathematical terms, we can write it like this:
(sin θ)2 + (cos θ)2 = 1
When the value of a trigonometric function is squared, the exponent 2 is customarily placed after the abbreviation of the function, so the parentheses can be eliminated from the expression. Therefore, the above equation is more often written this way:
sin2 θ + cos2 θ = 1
The difference between the squares of the secant and tangent of an angle is always equal to either 1 or –1. The following formulas apply for all angles except θ = 90° (π/2 rad) and θ = 270° (3π/2 rad):
sec2 θ – tan2 θ = 1
tan2 θ – sec2 θ = –1
Trigonometry is a branch of mathematics with extensive applications in science, engineering, architecture – even in art. You should not be shy about using a calculator and making sketches to help yourself solve problems. So what if they’re “crutches”? As long as you get the correct answer, you can use any help you need. (Just be sure you keep a fresh, spare battery around for your calculator if it’s battery powered.)
Use a drawing of the unit circle to help show why it is true that sin2 θ + cos2 θ = 1 for angles θ greater than 0° and less than 90°. (Hint: a right triangle is involved.)
Figure 12-10 shows a drawing of the unit circle, with θ defined counterclockwise between the x axis and a ray emanating from the origin. When the angle is greater than 0° but less than 90°, a right triangle is formed, with a segment of the ray as the hypotenuse. The length of this segment is equal to the radius of the unit circle. This radius, by definition, is 1 unit. According to the Pythagorean theorem for right triangles, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other
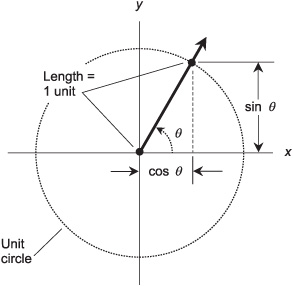
Fig. 12-10. Illustration for Problem 12-7.
Fig. 12-11. Illustration for Problem 12-8.
two sides. It is easy to see from Fig. 12-9 that the lengths of these other two sides are sin θ and cos θ. Therefore:
(sin θ)2 + (sin θ)2 = 12
which is the same as saying that sin2 θ + cos2 θ = 1.
Use another drawing of the unit circle to help show why it is true that sin2 θ + cos2 θ = 1 for angles θ greater than 270° and less than 360°. (Hint: this range can be considered, in directional terms, as equivalent to the range of angles greater than –90° and less than 0°.)
Figure 12-11 shows how this can be done. Draw a mirror image of Fig. 12-10, with the angle θ defined clockwise instead of counterclockwise. Again we have a right triangle. This triangle, like all right triangles, obeys the Pythagorean theorem.
Refer to the text in this chapter if necessary. A good score is eight correct. Answers are in the back of the book.
1. Suppose you stand on a flat, level surface on a sunny morning. Your shadow is exactly four times as long as you are tall. What is the angle of the sun above the horizon, to the nearest degree?
(a) 14°
(b) 45°
(c) 76°
(d) More information is needed to answer this question.
2. Suppose you stand on a flat, level surface on a sunny morning. The sun is at an angle of 50° above the horizon. You are exactly 160 centimeters (cm) tall. How long is your shadow, to the nearest centimeter?
(a) 122 cm
(b) 134 cm
(c) 190 cm
(d) More information is needed to answer this question.
3. Imagine that you stand some distance away from a tall building with a flat roof. The earth in the vicinity of the building is flat and level. The angle between the horizon and the top of the building, as measured from a point at your feet, is 70.00°. The straight-line distance between your feet and the nearest point at the top of the building is 200 meters (m). How tall is the building, to the nearest meter?
(a) 115 m
(b) 188 m
(c) 213 m
(d) More information is needed to answer this question.
4. One arc second is the equivalent of
(a) 1/60 of an arc minute
(b) 1/3600 of an arc minute
(c) 1/π of an arc minute
(d) 1/(2π) of an arc minute
5. Approximately how many degrees are there in 1 rad?
(a) 32.7°
(b) 45°
(c) 57.3°
(d) None of the above.
6. Suppose an almanac lists the latitude of your town as 35° 15′ 00″ N. This is equivalent to
(a) 35.15° N
(b) 35.25° N
(c) 35.50° N
(d) None of the above.
7. What is the angle, in radians, representing revolution by 3/4 of a circle in a clockwise direction?
(a) 3π/4
(b) –3π/4
(c) 3π/2
(d) –3π/2
8. The circumference of the earth is approximately 40,000 kilometers (km). What is the angular separation between two points 111 km apart, measured over the shortest possible path on the surface? Neglect irregularities in the terrain. Assume the earth is a perfect sphere.
(a) 1 rad
(b) 57.3°
(c) 1/360 rad
(d) 1°
9. Suppose you live in a remote area and decide to install an outdoor antenna for receiving stereo FM broadcasts. You buy a support tower that is 20.00 meters (m) high. The installation guide recommends guying the tower from a point halfway up, and also from the top. The guide also recommends that all guy wires be sloped at angles no greater than 45° with respect to the horizontal. Suppose you install two sets of guy wires, one set from a point halfway up and the other set from the top. All guys are fastened to three anchors at ground level. Each guy anchor is at just the right distance from the base of the tower to make the top set of guy wires slant at precisely 45.00°. At what angle, to the nearest tenth of a degree and relative to the horizontal, does each of the lower-level guy wires slant? Assume the ground in the vicinity of the tower is flat and level.
(a) 22.5°
(b) 26.6°
(c) 30.0°
(d) More information is needed to answer this question.
10. What is the largest possible value for the tangent of an angle?
(a) 1
(b) 90°
(c) π rad
(d) None of the above.