Every triangle has three angles and three sides. There are special ways to refer to the angles and sides of a triangle and their relationship between each other. The words adjacent, opposite, and included are used to refer to the relationships between the sides and angles of a triangle.
and 
are both adjacent to ∠A.
and 
are both adjacent to ∠B.
and 
are both adjacent to ∠C.
is included between ∠A and ∠B.
is included between ∠A and ∠C.
is included between ∠B and ∠C.
∠A is included between and .
∠B is included between and .
∠C is included between and .
is opposite angle ∠A.
is opposite angle ∠C.
is opposite angle ∠B.
Midpoint Theorem: The segment joining the midpoint of two sides of a triangle is parallel to the third side and half as long as the third side.
In triangle ABC, the midpoints of , , and are the points D, E, and F, respectively. 
connects the midpoints of and and is parallel to . is half as long as . = 
= 
.
connects the midpoints of and and is half as long as . is also parallel to . = 
= 
.
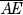connects and and is half as long as . is also parallel to . = 
= 
.
EXAMPLE:
If D is the midpoint of and E is the midpoint of , then is parallel to , and the length of is half the length of . If = 3, what is the length of ?
EXAMPLE:
In an isosceles triangle with sides of 10 and a base of 4, what are the lengths of , , and ?
Step 1:Find the length of side . Since = 4, = 
.
Step 2:Find the length of side . Since = 10, = 
.
Step 3:Find the length of sides . Since = 10, = 
.
The result is an isosceles triangle with sides 5, 5, 2.
Triangle ABC is an equilateral triangle. All the sides are equal. All the angles are equal. Points D, E, and F are midpoints. If = 10, what are the lengths of the following segments?
5.What type of triangle is triangle DEF?
6.What is the measure of angle DEF?
(Answers)
If triangle ABC is an isosceles right triangle and is 4 inches, what are the lengths of the following segments?
(Answers)
Look at triangle XYZ.
1.What angle is opposite 
?
2.What side is opposite ∠YZX?
3.What angle is included between 
and ?
4.What side is included between ∠Y and ∠Z?
(Answers)
Look at these two triangles.
Triangle ABC
Triangle DEF
m∠ABC = m∠DEF
m∠BCA = m∠EFD
m∠CAB = m∠FDE
is not equal to .
is not equal to .
is not equal to 
.
These two triangles are not congruent, but they are similar.
•Similar triangles have equal angles, but they do not have equal sides.
•If two triangles are similar, one looks like a larger or smaller version of the other.
•If two triangles are similar, the sides of one are in direct proportion to the sides of the other.
•If two triangles are similar, the ratio of corresponding sides of one triangle is equal to the ratio of corresponding sides of another triangle.
You can prove two triangles are similar using the AA Similarity Postulate.
Angle-Angle (AA) Similarity Postulate
If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar.
Look at these two similar triangles.
If these two triangles are similar, then
You can use the ratios to find the length of missing sides of a triangle.
EXAMPLE:
These two triangles are similar.
Find the length of and .
First match up corresponding sides.
Now substitute the sides you know.
Take one pair of ratios.
Cross-multiply to solve.
Now solve for .
If triangle ABC and triangle ECD are similar and if = 2, = 1, = 5, and 
= 6, find and 
.
(Answers)
RIGHT TRIANGLE PROPORTIONS THEOREM
Triangle ABC is a right triangle. Angle BAC is a right angle. Angle ABC and angle ACB are acute angles. is the altitude of the triangle. The hypotenuse is now divided into two segments, 
and 
. The altitude of a right triangle is a line segment from the vertex of the right angle perpendicular to the hypotenuse.
Now there are three triangles: a large right triangle, triangle ABC; a medium right triangle, triangle ABD; a small right triangle, triangle ADC.
The three triangles are similar but not congruent to each other. Triangle ABC, triangle ABD, and triangle ADC have the same shape but they are not the same size. Their corresponding angles are equal. The right angles are equal: angle BAC = angle ADB = angle ADC. The smaller of the two acute angles in each of the triangles are also equal: angle ABC = angle ABD = angle CAD. The larger of the two acute angles in each of the triangles are also equal: angle ACB = angle BAD = angle ACD.
Theorem: If an altitude is drawn from the right angle of any right triangle, then the two triangles formed are similar to the original triangle and similar to each other.
The small triangle (ACD) and the large triangle (ABC) are similar to each other. The short leg of the small triangle divided by the hypotenuse of the small triangle = the short leg of the large triangle divided by the hypotenuse of the large triangle. Notice that segment AC is both the hypotenuse of the small triangle and the short leg of the large triangle.
The medium triangle (ABD) and the large triangle (ABC) are similar to each other. The large leg of the medium triangle divided by the hypotenuse of the medium triangle = the large leg of the large triangle divided by the hypotenuse of the large triangle. Notice that segment AB is both the hypotenuse of the medium triangle and the large leg of the large triangle.
The small triangle ACD and medium triangle ABD are similar to each other. The small leg of the small triangle divided by the large leg of the small triangle = the small leg of the medium triangle divided by the large leg of the medium triangle. Notice segment AD is both the large leg of the small triangle and the small leg of the medium triangle.
Understanding these ratios makes it possible to solve ratio problems.
EXAMPLE:
Triangle ABC is a right triangle. Angle BAC is a right angle. Segment BC is the hypotenuse of the triangle. Segment AD is the altitude of triangle ABC. Angle ADB and Angle ADC are right angles. Assume side DC = 5 and side BC = 20. Find the lengths of sides AB and AC.
Step 1:Find .
Step 2:Use the proportions to find .
Step 3:Use the proportions to find .
Triangle ABC is a right triangle. Angle BAC is a right angle. Segment BC is the hypotenuse of triangle ABC. Segment AD is the altitude of triangle ABC. Angle ADB and angle ADC are right angles. Assume = 12 and = 9.
1.What is the measure of ?
2.What is the measure of ?
(Answers)
Triangle ABC is a right triangle. is the hypotenuse of triangle ABC. is the altitude.
= 16 and = 20.
1.Find .
2.Find .
3.Find .
4.Find .
(Answers)
Congruent triangles have the same size and the same shape. Two triangles are congruent if their angles are congruent and their sides are congruent.
These two triangles are congruent.
∠B ≅ ∠E
∠C ≅ ∠F
≅
≅
≅
In order for two triangles to be congruent, all six of these statements must be true.
If two triangles are congruent, then their corresponding parts are congruent.
EXAMPLE:
If triangle ABC is congruent to triangle DEF and the measure of angle ABC is 90 degrees, then the measure of angle DEF is also 90 degrees.
If triangle ABC is congruent to triangle DEF and side AB = 4, then side DE = 4.
Triangle ABC is congruent to triangle XYZ.
The measure of angle B = 90, the measure of angle A = 20, and 
= 2.
1.What is the m∠X?
2.What is the m∠Y ?
3.What is the m∠Z?
4.What is the length of ?
(Answers)
Corresponding angles and sides
When two triangles are congruent, all pairs of corresponding sides and all pairs of corresponding angles are congruent. Corresponding sides and angles are the sides and angles that match up between two triangles. Mathematicians use slash marks to indicate corresponding sides or angles.
EXAMPLE:
The single slash mark means is congruent to . The double slash mark means is congruent to . The triple slash mark means is congruent to .
SSS Postulate
If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
EXAMPLE:
To prove triangle ABC ≅ triangle XYZ, show that AB ≅ XY, AC ≅ XZ, and BC ≅ YZ.
MINI-PROOF
Figure ABDC is a rectangle.
Show that triangle ABD is congruent to triangle ACD.
To prove these two triangles congruent, show that all three sides are equal to each other. In other words, ≅ , ≅ , and ≅ .
1.Figure ABDC is a rectangle.
2. is a diagonal of rectangle ABDC.
Next list what you can infer based on what you know.
3. ≅ since they are opposite sides of a rectangle, and opposite sides of a rectangle are always congruent.
4. ≅ since they are opposite sides of a rectangle, and opposite sides of a rectangle are always congruent.
5. ≅ since every line segment is congruent to itself.
Conclusion
Since all three sides of one triangle are congruent to all three sides of the other triangle, the triangles are congruent. Since the triangles are congruent,
∠ABD ≅ ∠ACD
∠DAB ≅ ∠ADC
∠BDA ≅ ∠CAD
SAS Postulate
If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the triangles are congruent.
EXAMPLE:
To prove ΔABC = ΔXYZ, show that ≅ , ≅ , and ∠A is congruent to ∠X. ∠A is included between and , and ∠X is included between and . You can also prove that ΔABC is congruent to ΔXYZ using ∠B and ∠Y and their adjacent sides, or ∠C and ∠Z and their adjacent sides.
MINI-PROOF
Figure WXZY is a rhombus.
and are diagonals of the rhombus. Is ΔWEY congruent to ΔZEX?
To prove triangles WEY and ZEX congruent using SAS, show that two sides and an included angle of one triangle are congruent to two sides and an included angle of another triangle.
First list what you know.
1.Figure WXZY is a rhombus.
2. is a diagonal of the rhombus.
3. is a diagonal of the rhombus.
Next list what you can infer based on what you know.
4.The m∠WEY = m∠XEZ since they are vertical angles, and all vertical angles are equal. Since the measures are equal, the angles are congruent.
5. bisects since the diagonals of a rhombus bisect each other.
6.
= 
since a bisected line segment is divided into two congruent segments.
7. 
= 
since a bisected line segment is divided into two congruent segments.
Conclusion
ΔWEY is congruent to ΔZEX since two sides and the included angle of one triangle are congruent to two sides and the included angles of another triangle.
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
EXAMPLE:
To prove triangle ABC is congruent to triangle XYZ you must show that angle A is congruent to angle X, angle B is congruent to angle Y, and the included side AB is congruent to the included side XY.
MINI-PROOF
Figure ABCD is a square. and are diagonals of the square. Prove triangle ADC is congruent to triangle BCD.
First list what you know.
1.ABDC is a square.
2. is a diagonal of square ABDC.
3. is a diagonal of square ABDC.
Next list what you can infer from what you know.
4. = since every segment is congruent to itself.
5.∠C ≅ ∠D since they are both right angles.
6. = since the diagonals of a square are congruent.
7. = 
since the diagonals of a square bisect each other.
8.ΔECD is an isosceles triangle.
9.∠ECD ≅ ∠EDC, since the base angles of an isosceles triangle are congruent.
Conclusion
Using the ASA postulate, ΔADC and ΔBCD are congruent since two angles and the included side of each triangle are congruent. You could also prove these two triangles congruent using SAS.
Theorem: Two triangles are congruent if two angles and the side opposite one of them are congruent.
EXAMPLE:
To prove ΔABC ≅ ΔXYZ:
•show that ∠A ≅ ∠X and ∠B ≅ ∠Y. Now show that ≅ 
or ≅ , since these are all nonincluded sides.
or
•show that ∠B ≅ ∠Y and ∠C ≅ ∠Z and either ≅ or ≅ , since these are all nonincluded sides.
or
•show that ∠A ≅ ∠X and ∠C ≅ ∠Z and ≅ or ≅ , since these are all nonincluded sides.
MINI-PROOF
ABDC is a parallelogram. A parallelogram is a four-sided figure in which opposite sides are parallel and equal. is perpendicular to and .
Prove that ΔACD is congruent to ΔDBA.
First list what you know.
1.ABDC is a parallelogram.
2. is perpendicular to and .
What does this mean?
3.∠B ≅ ∠C, since the opposite angles of a parallelogram are congruent.
4. ≅ , since every segment is congruent to itself.
5.∠ADC and ∠DAB are right angles.
6.m∠ADC = m∠DAB, since all right angles are 90 degrees.
Conclusion
ΔACD is congruent to ΔDBA, since two angles and a nonincluded side of one triangle are equal to two angles and a nonincluded side of another triangle.
Hypotenuse-Leg Postulate
Two right triangles are congruent if the hypotenuse and leg of one right triangle are congruent to the hypotenuse and leg of another right triangle.
To prove that these two right triangles are congruent, just show that hypotenuse is congruent to hypotenuse and leg is congruent to leg . Or show that hypotenuse is congruent to hypotenuse and leg is congruent to leg .
MINI-PROOF
Triangle ABC is an isosceles triangle where ≅ .
is the perpendicular bisector of . Prove ΔABD ≅ ΔACD.
First list what you know.
1.Triangle ABC is an isosceles triangle.
2. is the altitude of ΔABC.
What does this mean?
3. is perpendicular to since is an altitude of triangle ABC.
4.Angle ADB and angle ADC are both right angles since is perpendicular to .
5.Triangle ADB and triangle ADC are both right triangles, since angle ADB and angle ADC are both right angles.
6.The hypotenuse of triangle ABD is congruent to the hypotenuse of triangle ACD, since triangle ABC is an isosceles triangle.
7.One leg of triangle ABD is congruent to one leg of triangle ACD, since is a leg of both triangles and congruent to itself.
Conclusion
Triangle ABD is congruent to triangle ACD because of the hypotenuse-leg postulate. The hypotenuse and one leg of triangle ABD is congruent to the hypotenuse and one leg of triangle ACD.
