
A polygon is a two-dimensional closed shape made up of line segments. It has a minimum of three sides. A triangle is a polygon, so is a square, a rectangle, a rhombus, a pentagon, and a hexagon. A circle is not a polygon. It is a closed shape but it’s not made up of line segments.
A polygon can have three sides, five sides, or one hundred sides. If all sides of a polygon are the same length, then it is an equilateral polygon. A rhombus is an equilateral polygon. All four sides of the rhombus are the same length, but the four angles of a rhombus are not the same size.

All angles in an equiangular polygon have the same measurement. A rectangle is an equiangular polygon. All four angles are 90 degrees. It is not an equilateral polygon because all four sides are not the same length.

REGULAR AND IRREGULAR POLYGONS
All the sides and all the angles in a regular polygon are equal. A square is a regular polygon.

All parallelograms are polygons. A square, a rhombus, and a rectangle are all polygons. A square is a regular polygon, but a rhombus and a rectangle are irregular.
A polygon is called irregular when the sides or angles are not equal.

Polygons are also classified as concave or convex. A convex polygon is a polygon where all the angles are less than 180 degrees. This trapezoid, a rectangle, and a dodecagon are all convex polygons.

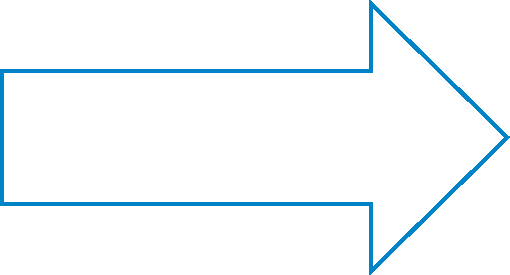
Concave polygons look entirely different. In a concave polygon, at least one of the angles in the polygon is greater than 180 degrees. The arrow below is a concave polygon. There are seven angles in this arrow. Two of the angles are greater than 180 degrees. The arrow is also an irregular polygon.
Polygons are named by the number of sides.
An equiangular triangle is a regular polygon with three sides. Each of the angles of an equilateral triangle is 60 degrees. The total number of degrees in a triangle is 180 degrees.

A square is a regular polygon with four equal sides. Each of the interior angles of a square is 90 degrees. The total number of degrees in a square is 4 × 90 degrees, or 360 degrees. A square has 180 degrees more than a triangle.

A regular pentagon is a polygon with five equal sides. Each of the interior angles of a regular pentagon is 108 degrees. The total number of degrees in a pentagon is 5 × 108 degrees, or 540 degrees. A pentagon has a total of 180 degrees more than a square.
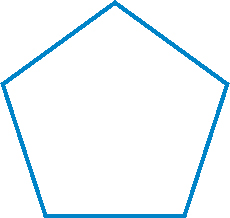
A regular hexagon is a polygon with six equal sides. Each of the interior angles of the hexagon is 120 degrees. The total number of degrees in a hexagon is 6 × 120 degrees, or 720 degrees. A hexagon has a total of 180 degrees more than a pentagon.
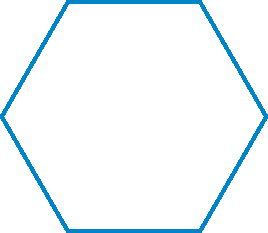
A regular heptagon is a polygon with seven equal sides. Each of the angles of a heptagon is 128.571 degrees. The total number of degrees in a heptagon is 900 degrees. A heptagon has a total of 180 degrees more than a hexagon.
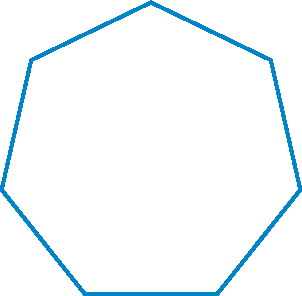
A regular octagon is a polygon with eight equal sides. Each of the angles of an octagon is 135 degrees. The total number of degrees in an octagon is 1,080 degrees. An octagon has a total of 180 degrees more than a heptagon.
It is possible to compute the sum of interior angles of any regular polygon. Just subtract 2 from the number of sides in the polygon, and multiply the result by 180. Watch—it’s painless.
Theorem: The sum of the interior angles of a regular polygon = (n – 2)180 degrees, where n is the number of sides in the polygon.
What is the sum of the angles in a regular hexagon?
Sum = (n – 2)180, where n is the number of sides in a hexagon.
Sum = (6 – 2)180 degrees
Sum = 4(180) = 720 degrees
The sum of the angles of a hexagon is 720 degrees.
EXAMPLE:
What is the sum of the angles in a regular dodecagon? Hint: A dodecagon is a polygon with twelve sides.
Sum = (n – 2)180, where n is the number of sides in a regular dodecagon.
Sum = (12 – 2)180
10(180) = 1,800
The sum of the angles of a regular dodecagon is 1,800 degrees.
EXAMPLE:
What is the sum of the angles in a regular polygon with twenty sides?
Sum = (n – 2)180, where n is the number of sides in the polygon.
Sum = (20 – 2)180
18(180) = 3,240
The sum of the angles of a regular polygon with 20 sides is 3,240 degrees.
Once you know the total number of degrees inside a regular polygon, it’s easy to figure out how many degrees in each angle.
Theorem: Each interior angle (of a regular polygon) 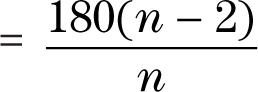 degrees, where n is the number of sides in the polygon.
degrees, where n is the number of sides in the polygon.
To compute the size of the interior angles of a regular polygon, follow these two painless steps.
Step 1:Compute the total number of degrees in the regular polygon.
Step 2:Divide the total number of degrees by the number of sides.
EXAMPLE:
Compute the size of each interior angle of a regular octagon.
An octagon has eight sides.
Step 1:Find the total number of degrees in an octagon.
Total degrees = (n – 2)180, where n is the number of sides in an octagon.
Total degrees = (8 – 2)180
Total degrees = 6(180) = 1,080
Step 2:Divide the total number of degrees by the number of sides.
Measure of one interior angle = 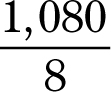
The measure of one interior angle of an octagon is 135 degrees.
EXAMPLE:
Compute the size of each interior angle in a regular polygon with thirty sides.
Step 1:Find the total number of degrees in the polygon.
Total degrees = (n – 2)180, where n is the number of sides.
Total degrees = (30 – 2)180
Total degrees = 28(180) = 5,040
Step 2:Divide the total number of degrees by the number of sides in the polygon.
The measure of one interior angle = 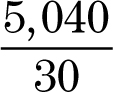 .
.
The measure of one interior angle of a regular polygon with 30 sides is 168 degrees.
1.Find the total number of degrees in a regular polygon with 11 sides.
2.Find the total number of degrees in a regular polygon with 100 sides.
3.Find the number of degrees of a single angle in a regular polygon with 15 sides.
4.Find the number of degrees of a single angle in a regular polygon with 25 sides.
(Answers)
For each interior angle of a regular polygon there is a corresponding exterior angle. The exterior angle is the angle between any side of the polygon and a line extended from the next side of the polygon.
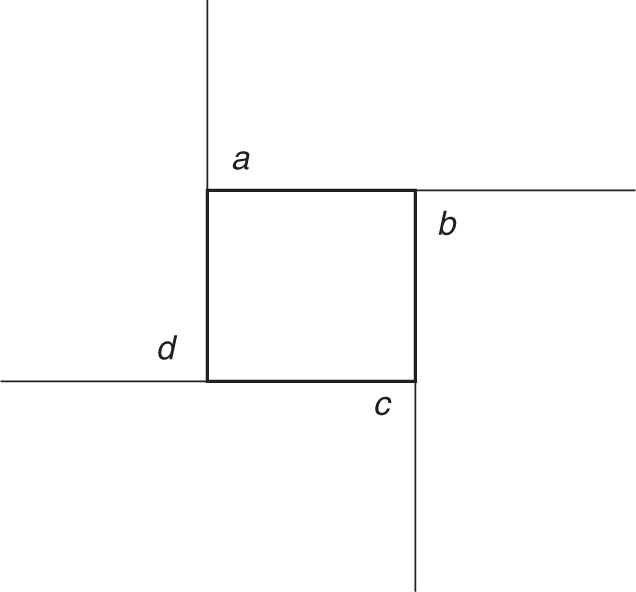
This square is a polygon. Extending each of the sides of the square in one direction creates four exterior angles, angles a, b, c, and d. Each of these angles is a right angle. The sum of these four angles is 360 degrees.
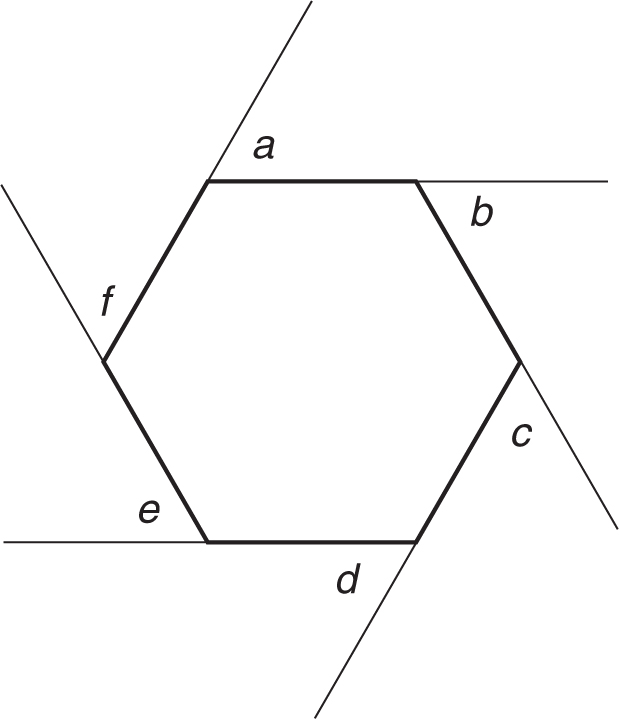
Each of the sides of this hexagon have been extended in one direction to create six exterior angles, angles a, b, c, d, e, and f. Since all the interior angles are equal, all the exterior angles are equal to each other. The sum of the exterior angles of this hexagon is also 360 degrees.
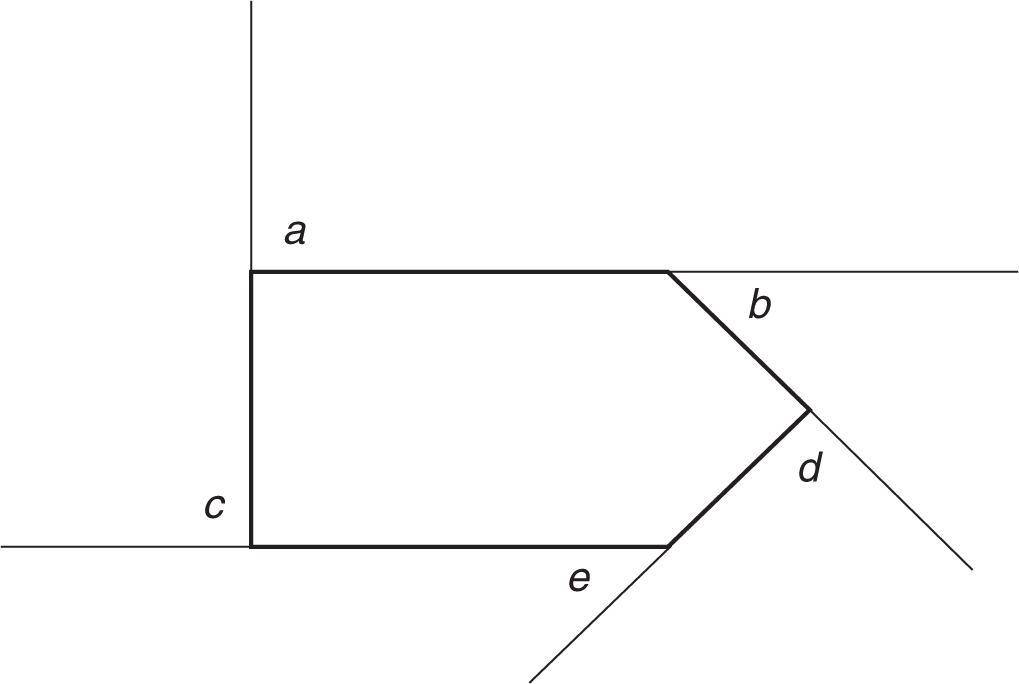
Irregular polygons have exterior angles also. The five sides of this pentagon were extended to create five exterior angles, angles a, b, c, d, and e. The five interior angles of this pentagon are not equal, so the five exterior angles of this pentagon are not equal.
The sum of the exterior angles of a regular polygon will always equal 360 degrees no matter how many sides the polygon has.
Theorem: To measure an exterior angle of a regular polygon, divide 360 by the number of sides of the polygon.
Size of exterior angle of a regular polygon = 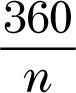
(n is equal to the number of sides on the polygon)
EXAMPLE:
What is the size of the exterior angle of a regular hexagon? Divide 360 by 6, which is the number of sides in the hexagon.
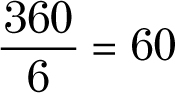
EXAMPLE:
What is the measure of the exterior angle of a regular polygon with ten sides?
Divide 360 by 10, which is the number of sides in the polygon.
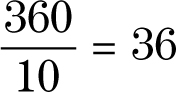
Theorem: The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180 degrees.
If the interior angle of a regular pentagon is 108 degrees, then the corresponding exterior angle is 180 – 108 = 72. If the exterior angle of a regular octagon is 45 degrees, then the corresponding interior angle is 180 – 45 = 135.
If you know the interior angle of a regular polygon, it’s easy to calculate the number of sides. Just follow these two painless steps.
Step 1:Calculate the size of the exterior angles of a polygon by subtracting the size of the interior angle from 180.
Step 2:Divide 360 by the size of a single exterior angle.
EXAMPLE:
The interior angles of a regular polygon are each 140 degrees. How many sides does the polygon have?
Step 1:Calculate the size of a single exterior angle by subtracting the size of the interior angle from 180.
180 – 140 = 40
Step 2:Divide 360 by the size of a single exterior angle.
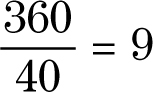
The polygon has nine sides. It’s a nonagon!
EXAMPLE:
The interior angles of a regular polygon are each 135 degrees. How many sides does the polygon have?
Step 1:Calculate the size of the exterior angle.
180 – 135 = 45
Step 2:Divide 360 by the size of a single interior angle.
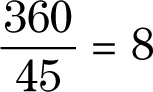
This polygon has eight sides. It’s an octagon!

1.If the interior angle of a regular polygon is 170 degrees, what is the measure of the corresponding exterior angle?
2.If the interior angle of a regular polygon is 30 degrees, what is the measure of the corresponding exterior angle?
3.If the interior angle of a regular polygon has 150 degrees, how many sides does the polygon have?
4.If the interior angle of a regular polygon has 160 degrees, how many sides does the polygon have?
(Answers)
INSCRIBED AND CIRCUMSCRIBED POLYGONS
The words inscribe and circumscribe have special meanings in geometry. To inscribe means to put one shape inside another shape. To circumscribe a shape means to put a figure around it. It’s possible to inscribe regular polygons inside circles. It’s also possible to inscribe circles inside polygons.
This regular pentagon is inscribed in the circle. The vertices of the pentagon are points on the circle. The center of the circle is the center of the pentagon.

This circle is inscribed in a regular hexagon. The sides of the hexagon are tangent to the circle. The center of the circle is the center of the hexagon. This hexagon is circumscribed around this circle. All six sides of the hexagon are tangent to the circle.

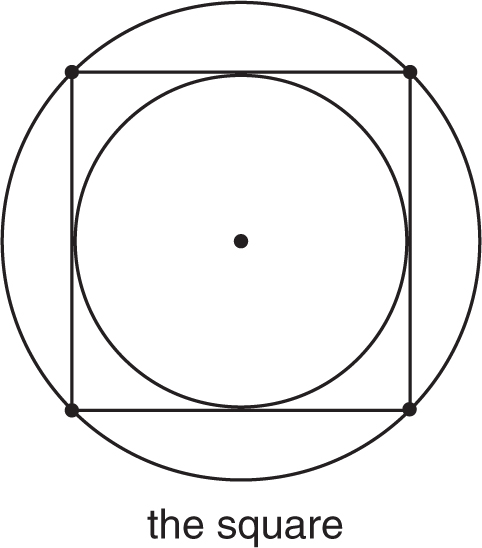
This square is both inscribed inside the larger circle and circumscribed around the smaller circle. The center of the square is the center of both of the circles. The sides of the square are tangent to the small circle. The vertices of the square lie on the large circle.

1.Find the total number of degrees in a regular polygon with fifteen sides.
2.Find the number of degrees in a single angle of a regular polygon with seventeen sides.
3.If the interior angle of a regular polygon is 40 degrees, what is the measure of the corresponding exterior angle?
4.If the interior angle of a regular polygon is 144 degrees, how many sides does the polygon have?
(Answers)