Circles are everywhere. A wheel is in the shape of a circle. So are the face of a clock, the rim of a plate, and the lip of a cup. Circles are unique geometric shapes. Every circle has three things in common.
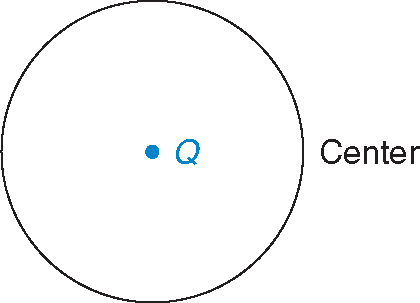
1.Every circle has a center. The center is a fixed point in the middle of the circle.
2.Every point the exact same distance from the center of the circle is on the circle.
3.All the points in a circle are on a single plane.
Circles are usually named by their center. This is circle Q.
Experiment
Learn a creative way to make a circle.
Materials
Piece of string 5-inches long
Two pencils
Paper
Procedure
1.Tie one end of the piece of string tightly around a pencil.
2.Tie the other end of the string around a second pencil.
3.Place one of the pencils, point down, firmly in the center of a piece of paper.
4.Keeping the string tight, draw a circle by moving the second pencil around the first.
5.Use a different length of string and draw a different size circle with the same center.
Something to think about . . .
How does a compass work to draw circles?
What else could you use to draw a circle?
Concentric circles are circles with the same center.
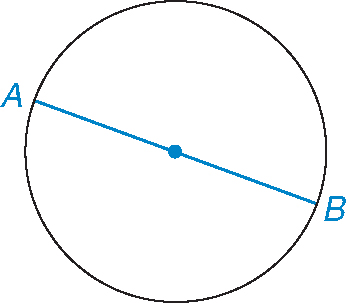
The radius of a circle is a line segment that starts at the center of the circle and ends on the circle. Every radius of the same circle is exactly the same length.
EXAMPLE:
, 
, 
, and 
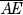are all radii of the circle.
All these radii are the same length.
= = =
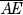
The diameter of a circle is a line segment that connects both sides of the circle and passes through the center of the circle. All diameters of a single circle are the same length.
EXAMPLE:
and 
are both diameters of circle Q.
=
Experiment
Discover the relationship between the radius and the diameter of a circle.
Materials
Compass
Paper
Pencil
Ruler
Procedure
1.Use a compass to draw a large circle.
2.Use the compass to draw a smaller circle.
3.Draw three lines through the center of each circle. These are the diameters of each circle.
4.Measure the length of each diameter. Enter the results in the chart.
5.Draw three radii in each circle.
6.Measure the length of each radius. Enter the results in the chart.
Small circle |
Large circle |
|
Radius 1 |
||
Radius 2 |
||
Radius 3 |
||
Diameter 1 |
||
Diameter 2 |
||
Diameter 3 |
Something to think about . . .
Are all the radii from one circle the same length?
Are all the diameters from one circle the same length?
What is the relationship between the length of the radius and the length of the diameter?
In geometry, “if and only if” statements are common. “If and only if” statements mean the first statement will always be true when the second is true, and will only be true if the second is true.
Theorem: Two circles are congruent if and only if their radii are the same length.
This theorem means two things:
1.Two circles are congrugent only if their radii are the same length. In other words, the circles cannot be congruent if the radii are not the same length.
2.Two circles are congrugent if their radii are the same length. Proving the radii are congruent is sufficient to prove that the circles are congruent.
You can prove that two circles are congruent if you can prove that either their radii or diameters are congruent.
1.If a circle has a 3-inch radius, what is the length of the diameter?
2.If a circle has a 12-inch diameter, what is the length of the radius?
(Answers)
A circle divides a plane into three distinct areas:
•interior of a circle
•exterior of a circle
•the circle itself.
The area inside the circle is called the interior of the circle. Points A, B, and C lie in the interior of the circle.
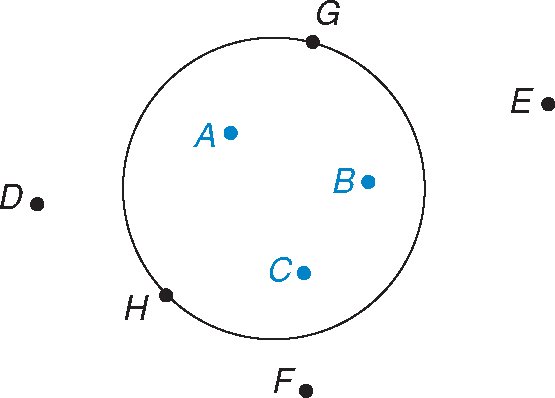
Points G and H lie on the circle. The exterior of the circle is all the points that are farther from the center of the circle than the length of the radius of the circle. Points D, E, and F lie in the exterior of a circle.
The distance from the center of the circle to any point inside the circle is less than the length of the radius. The distance from the center of the circle to any point in the exterior of the circle is greater than the length of the radius. The distance from the center of the circle to any point on the circle is exactly the length of the radius.
1.A circle has a radius of 4 inches. A point lies six inches from the center of the circle. Is this point on the circle, in the interior of the circle, or in the exterior of the circle?
2.A circle has a diameter of 10 inches. A point lies eight inches from the center of the circle. Is this point on the circle, in the interior of the circle, or in the exterior of the circle?
3.A circle has a diameter of 12 inches. A point lies six inches from the center of the circle. Is this point in the interior of the circle, in the exterior of the circle, or on the circle?
4.A circle has a radius of 5 inches. A point lies three inches from the center of the circle. Is this point in the interior of the circle, in the exterior of the circle, or on the circle?
(Answers)
π is a Greek symbol and is spelled as “pi” and pronounced “pie.” π is determined by dividing the circumference of a circle by its diameter. π is 3.141592 . . . and continues forever. π is a nonterminating, nonrepeating decimal. When you solve problems where you need the number π, use an approximation of π. The number 3.14 is a common approximation of π. So is 
. When π is involved, compute two decimal places.
Experiment
Determine the relationship between the circumference and the diameter of a circle.
Materials
String
Ruler
Pencil
Paper
Calculator
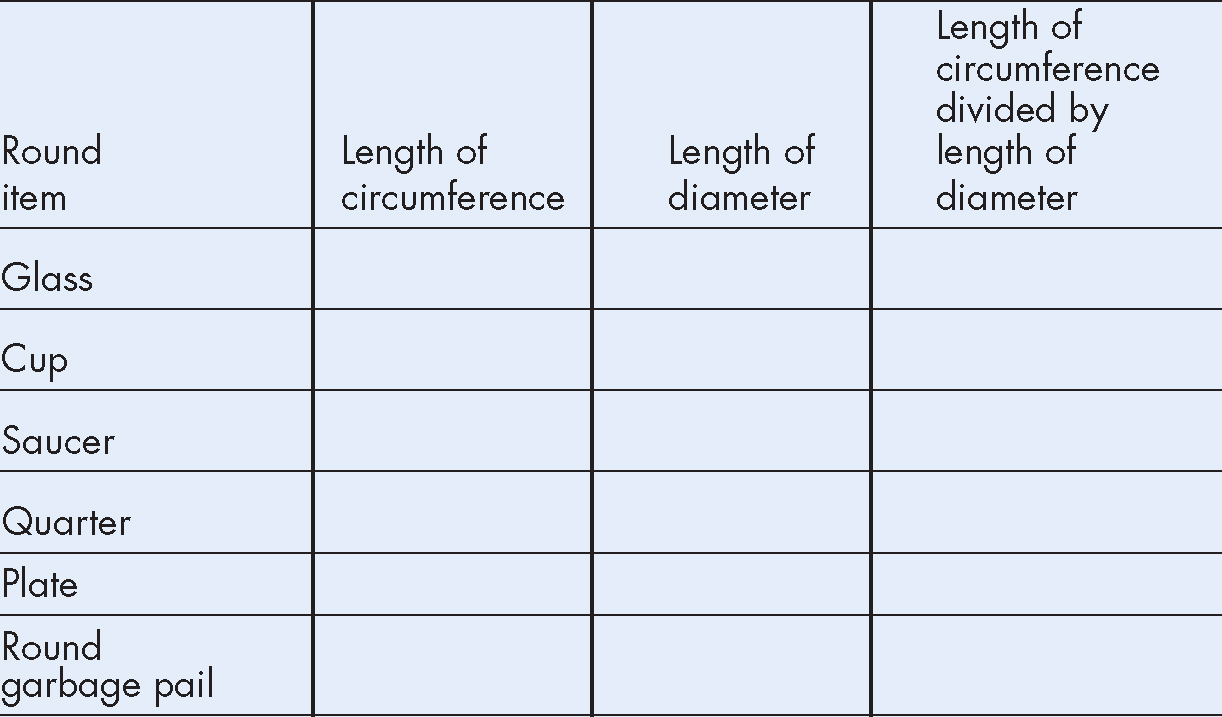
Plate, saucer, cup, glass, garbage pail, quarter, and other round items
1.Measure the distance around each round object by putting a string around each object. Measure the length of the string used to circle each item using the ruler. Write your findings in the chart.
2.Measure the length of the diameter using the ruler and the string. Make sure that the diameter goes through the center of the circle. Write your findings in the chart.
3.Divide the distance around each circle (circumference) by the distance across the center of the circle (diameter). Write your results in the chart.
4.Compare the results of column 3 for the glass, cup, saucer, quarter, plate, and garbage pail.
Something to think about . . .
If the diameter of one circle is twice as large as another circle, what is the relationship between the circumferences of these two circles?
The distance around a circle is called the circumference and is measured in linear units.
To figure out the circumference of a circle, follow these painless steps:
Step 1:Find the diameter of the circle.
Step 2:Multiply the diameter by π.
Circumference of a Circle
C = πd
d stands for the diameter of a circle.
To approximate the circumference of a circle, use either of these formulas:
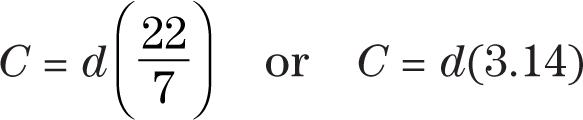
EXAMPLE:
Compute the circumference of a circle with diameter 4.
Computing the circumference of a circle using the radius is painless.
Step 1:Find the radius of the circle.
Step 2:Multiply the radius by 2 since the diameter is twice the radius.
Step 3:Multiply the diameter by π.
Circumference of a Circle
C = 2 πr
Compute the circumference of a circle with radius 1.
Step 1:Find the radius of the circle.
The radius is 1.
Step 2:Multiply the radius by 2 to find the diameter of the circle.
(2)(1) = 2
The diameter is 2.
Step 3:Multiply the diameter by π.
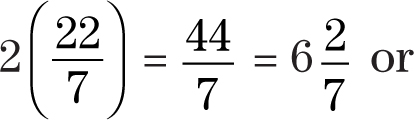
2(3.14) = 6.28
The circumference of the circle is 2π or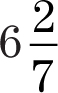 
or 6.28.
Theorem: Congruent circles have the same circumference.
1.Find the circumference of a circle with diameter 10 in terms of π.
2.Find the circumference of a circle with radius 5 in terms of π.
3.Find the circumference of a circle with radius in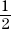 
terms of π.
4.Find the radius of a circle with circumference 6π.
(Answers)
The area of a circle is the area covered by the interior of the circle and the circle itself.
Experiment
Learn to approximate the area of a circle.
Materials
Graph paper
Pencil
Compass
Procedure
1.Draw a circle on a piece of graph paper.
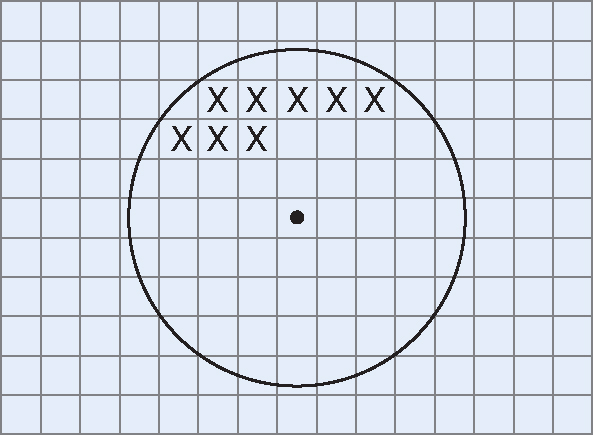
2.Count the number of complete squares inside the circle. Put an x on each square you count to make sure that you don’t count the same square twice. Write this number down.
3.Count the number of partial squares inside the circle. Shade each of these partial squares. Multiply the number of partial squares by 
. Write this number down.
4.Add the numbers in Step 2 and Step 3.
Something to think about . . .
Is there an easier way to find the area of a circle?
Finding the area of a circle is painless, especially if you state the answers in terms of π.
Step 1:Find the radius of the circle.
Step 2:Multiply π times the radius squared.
Area of a Circle
A = πr2
EXAMPLE:
Find the area of a circle with radius 3.
Area of a circle = π(3)2
Area of a circle = 9 π square units
You can also find the area of a circle if you know the diameter. Just square half the diameter and multiply the result by π.
Area of a Circle
EXAMPLE:
What is the area of a circle with a diameter of 8 inches?
First find the radius of the circle by multiplying the diameter by .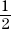
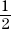(8) = 4 inches
Area of a circle = π(4)2
Area of a circle = 16π square inches
You can also find the area of a circle if you know the circumference. Just follow these painless steps:
Step 1:First divide the circumference by π to find the diameter.
Step 2:Divide the diameter by 2 to find the radius.
Step 3:Square the radius of the circle.
Step 4:Multiply the squared radius by π.
EXAMPLE:
Find the area of a circle with circumference 10π.
Step 1:First divide the circumference by π to find the diameter.
10π divided by π is 10.
The diameter of the circle is 10.
Step 2:Divide the diameter by 2 to find the radius of the circle.
10 divided by 2 is 5.
The radius of the circle is 5.
Step 3:Square the radius of the circle.
52 = 25
Step 4:Multiply the squared radius by π.
25π
The area of the circle is 25π square units.
1.What is the area of a circle with radius 10?
2.What is the area of a circle with diameter 2?
3.What is the area of a circle with circumference 20π?
(Answers)
Experiment
Compare the area of a circle with the area of a square.
Materials
Graph paper
Pencil
Calculator
Procedure
1.Draw a square with a side of 10 units on the graph paper.
2.Inscribe a circle inside the square. To inscribe a circle in a square, each side of the square should be touched by the circle once. This circle has a diameter of 10 units.
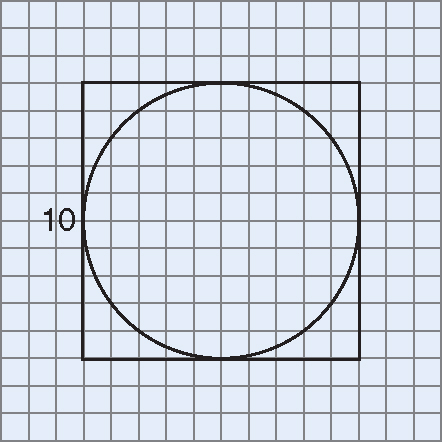
3.Compute the area of the square. (Area = s × s)
4.Computer the area of the circle. (Area = 3.14 × r × r)
6.Divide the area of the circle by the area of the square. Multiply the answer by 100 to change the answer to a percent.
7.What percent of the area of the square is the area of the circle?
8.Repeat the first seven steps for a circle with a diameter of 2 units and a square with side 2.
Something to think about . . .
How can the results be used to estimate the area of a circle? Inscribe a square in a circle. What percentage of the area of a circle is the area of a square?
Theorem: Congruent circles have the same area. If two circles have the same area, they must be congruent.
To prove two circles congruent, show that their
•radii are the same length.
•diameters are the same length.
•circumferences are the same length.
•areas are the same.
A right angle has a measure of 90 degrees. The measure of a straight angle is 180 degrees. One circular rotation equals 360°.
The degrees of a circle can be proven by measuring the central angles of a circle. A central angle is an angle whose vertex is the center of the circle and whose sides intersect the sides of a circle.
Angle ABC is a central angle. Use a protractor to measure a central angle.
Experiment
Discover the number of degrees in a circle.
Materials
Paper
Pencil
Protractor
Procedure
1.Measure each of the central angles in these circles using a protractor. Enter the results in the chart.
2.Add the measures of the angles. Enter your answer in the chart.
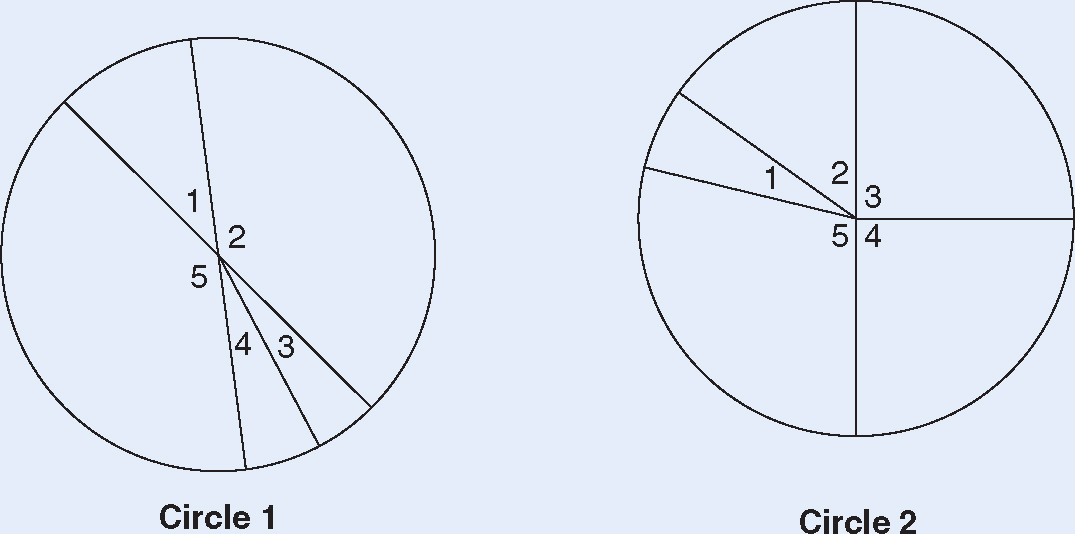
Circle 1 |
Circle 2 |
|
Angle 1 |
||
Angle 2 |
||
Angle 3 |
||
Angle 4 |
||
Angle 5 |
||
Total of angles 1, 2, 3, 4, and 5 |
Something to think about . . .
Draw a small circle approximately half the size of Circles 1 and 2. How many degrees are in this circle?
Draw a large circle approximately twice the size of Circles 1 and 2. How many degrees are in this circle?
Theorem: Every circle has a total of 360 degrees.
1.How many degrees are in a circle with radius 4?
2.How many degrees are in a circle with diameter 10?
3.How many degrees are in a circle with radius 100?
(Answers)
A chord is a line segment whose endpoints lie on the circle. Segments AB, CD, EF, and GH are all chords.
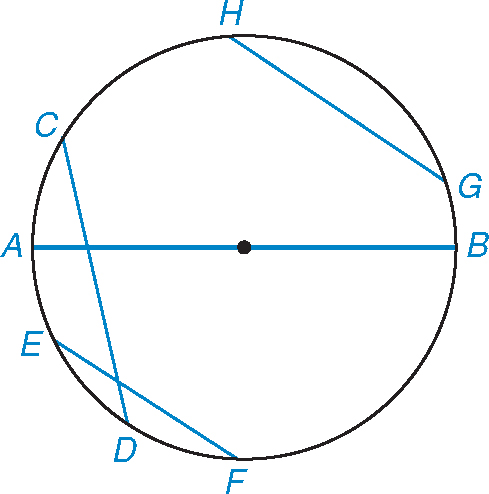
Notice that segment AB is both a chord and a diameter of the circle.
Which of these segments are chords?
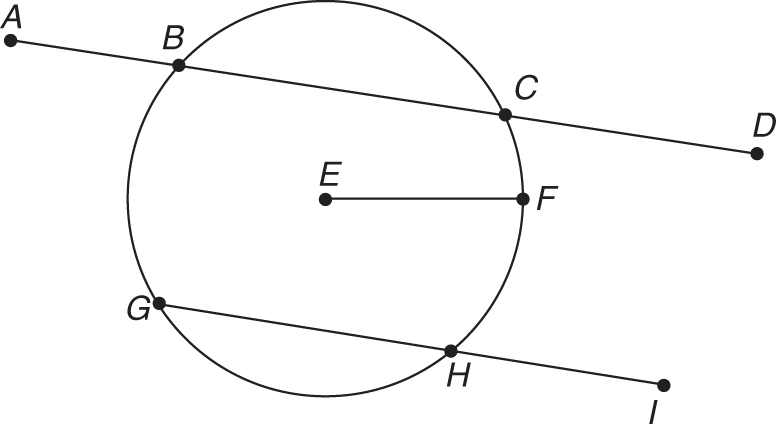
Segments AD and GI extend beyond the circle and are not chords. One of these segments (EF) is the radius of the circle. It contacts only one side of the circle. However, segments BC and GH are chords.
A tangent is a line on the exterior of the circle that touches the circle in exactly one point.
EXAMPLE:
Line RS is tangent to circle P.
The circle and the line intersect at exactly one point, R.
A secant is a line that intersects a circle at two points. Lines AB and CD are secants. These secants are parallel lines and do not intersect.
Lines LK and LM are also secants. They intersect at point N.
Decide whether each of the following statements is true or false.
1.A radius is a chord.
2.A tangent intersects a circle at two points.
3.A diameter is a chord.
4.A secant intersects a circle at only one point.
(Answers)
An arc is a portion of a circle.
A semicircle is an arc that is exactly half a circle. The endpoints of a semicircle lie on the diameter of a circle.
EXAMPLE:
Draw a circle. Draw a diameter and call it .
Each semicircle is called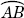 
.
Not all arcs are semicircles.
EXAMPLE:
Draw a circle and pick two points on the circle. These two points divide the circle into two arcs. One of the arcs is smaller than the other arc.
The smaller arc is called the minor arc. A minor arc is less than a semicircle. Label the minor arc using two letters. Place an arc sign over the letters. Arc AB is written as .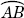
The larger arc is called a major arc. A major arc is larger than a semicircle. Label the major arc using three letters by picking another letter on the arc. Three letters are used to label major arcs so they are not confused with the minor arcs. Place an arc sign over the three letters. Arc ACB is written as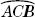 
.
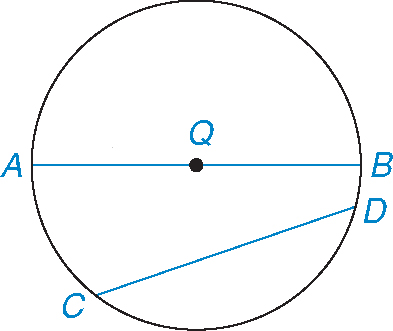
Determine whether each of the following statements is true or false.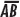 
is a diameter. 
is a chord that does not go through the center of the circle.
1.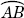 is a semicircle.
2.
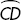is a major arc.
3.
is greater than a semicircle.
(Answers)
The measure of an arc is expressed in degrees, while the length of an arc is expressed in linear measurements such as inches, centimeters, and feet.
Finding the measure of an arc is easy. Just measure the central angle that the arc cuts off. Remember that a central angle is an angle that has its vertex as the center of the circle and its sides are radii of the circle.
To find the measure of an arc, just follow these painless steps:
Step 1:Draw a line segment from one end of the arc to the center of the circle.
Step 2:Draw a line segment from the other end of the arc to the center of the circle.
Step 3:Measure the angle created by the two line segments. If the arc is a minor arc (less than 180 degrees), this is the measure of the arc.
Step 4:If the arc is a major arc (greater than 180 degrees) subtract the measure of the angle from 360 degrees to find the measure of the major arc.
Find the measure of the arc indicated.
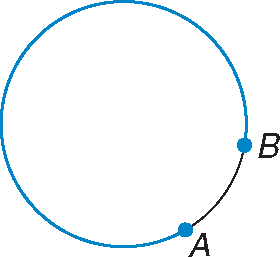
Step 1:Connect one end of the arc to the center of the circle.
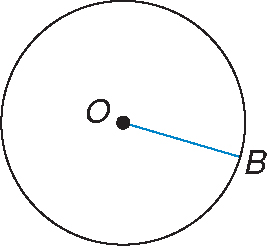
Step 2:Connect the other end of the arc to the center of the circle.
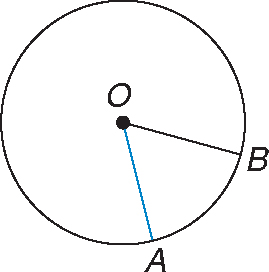
Step 3:Measure the angle created by the two line segments.
Angle AOB is 60 degrees.
Step 4:If the arc is a major arc (greater than 180 degrees), subtract the measure of the angle from 360 degrees to find the measure of the major arc. Since the arc is a major arc, subtract 60 degrees from 360 degrees.
360 – 60 = 300
The measure of the arc is 300 degrees.
To find the length of an arc, just follow these painless steps:
Step 1:Find the circumference of the circle.
Step 2:Divide the number of degrees in the arc by 360.
Step 3:Multiply the circumference of the circle by the ratio found in Step 2.
EXAMPLE:
Find the length of an arc with a measure of 30 degrees that is part of a circle with radius 12 inches.
Step 1:Find the circumference of the circle.
The circumference of the circle = π(diameter).
If the radius is 12, the diameter is 24.
The circumference is 24π.
Step 2:Divide the number of degrees in the arc by 360 degrees.
The arc is 30 degrees. So, 30 degrees divided by 360 degrees is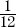 
.
Step 3:Multiply the circumference by the ratio.
Multiply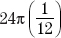 
.
The answer is 2π or 6.28.
A semicircle is half a circle. The endpoints of a semicircle are a diameter of a circle. A semicircle has an arc of 180 degrees.
To find the perimeter of a semicircle, follow these four painless steps:
Step 1:Find the circumference of the entire circle.
Step 2:Divide the circumference by 2 to find the length of the arc of the semicircle.
Step 3:Find the length of the diameter.
Step 4:Add the length of the arc to the length of the diameter.
EXAMPLE:
Find the circumference of a semicircle with diameter 10.
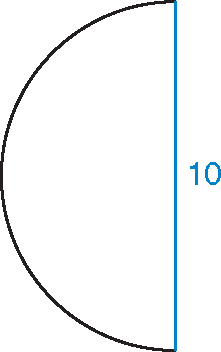
Step 1:Find the circumference of the entire circle. The circumference of the entire circle is 10(3.14) or 31.4.
Step 2:Divide the circumference by 2 to find the length of the arc of the semicircle.
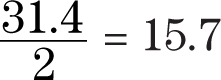
Step 3:Find the length of the diameter.
The length of the diameter is 10.
Step 4:Add the length of the arc (15.7) to the length of the diameter (10) to find the circumference of the semicircle.
15.7 + 10 = 25.7
Theorem: Congruent arcs have the same degree measure and the same length.
and have both the same measure and the same length.
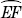and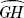 
are not congruent. They have the same length but not the same measure.
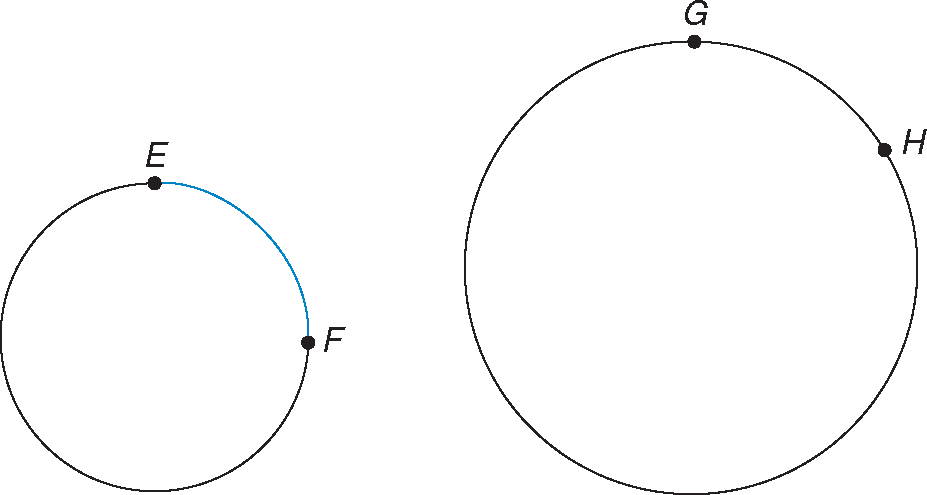
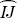and 
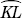are not congruent. They have the same measure but not the same length.
1.Find the length of an arc that is 180 degrees in a circle with diameter 4.
2.Find the length of an arc that is 270 degrees in a circle with diameter 10.
3.Find the length of an arc that is 45 degrees in a circle with diameter 2.
(Answers)
Eight different types of angles are formed when secants, tangents, radii, or chords of a circle intersect. The measure of each of these angles depends on the measure of the intersected arc. The vertex of these angles can be located inside a circle or outside a circle, or it can intersect a circle.
Case I: Two radii
An angle formed by two radii of a circle is called a central angle. The vertex of a central angle is the center of the circle. The measure of the central angle is equal to the measure of the intersected arc. Any two radii inside a circle will form a central angle.
EXAMPLE:
The measure of angle BAC = measure of arc BC.
If arc BC = 45 degrees then angle BAC = 45 degrees.
Likewise if angle BAC = 45 degrees, then arc BC = 45 degrees.
Case II: Two chords
An angle formed by two chords is called an inscribed angle. The vertex of the inscribed angle is on the circle. The measure of an inscribed angle is equal to half the measure of the intersected arc.
Angle ABD is formed by two chords.
The measure of angle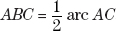 
.
If arc AC = 80 degrees, then angle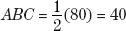 
.
Case III: Two tangents
The vertex on an angle formed by the intersection of two tangents is always outside the circle. The measure of an angle formed by two tangents is half the difference of the two intersected arcs. A third point on the circle (point D) is placed to differentiate between the major arc and the minor arc.
To find the measure of angle BAC, follow these three painless steps.
Step 1:Find the measure of both arcs.
Step 2:Subtract the measure of the minor arc from the measure of the major arc.
Step 3:Take half the difference.
Find the measure of angle BAC if arc BC = 90 degrees.
Step 1:Find the measure of arc BC and arc BDC.
If arc BC is 90 degrees, arc BDC is 360 – 90 = 270 degrees.
Step 2:Subtract the measure of arc BC from the measure of arc BDC.
270 – 90 = 180
Step 3:Take half the difference.
Angle BAC = 90 degrees.
Case IV: One tangent and one secant
A tangent and a secant can intersect outside the circle or on the circle. Since tangents have no points inside the circle, they never intersect inside the circle. This tangent and secant intersect outside the circle. The tangent intersects the circle at exactly one point, C. The secant intersects the circle at two points, B and D. Point A, where the secant and the tangent intersect, is the vertex of the angle. The measure of an angle formed by a tangent and a secant that intersect outside the circle is half the difference of the two intersected arcs.
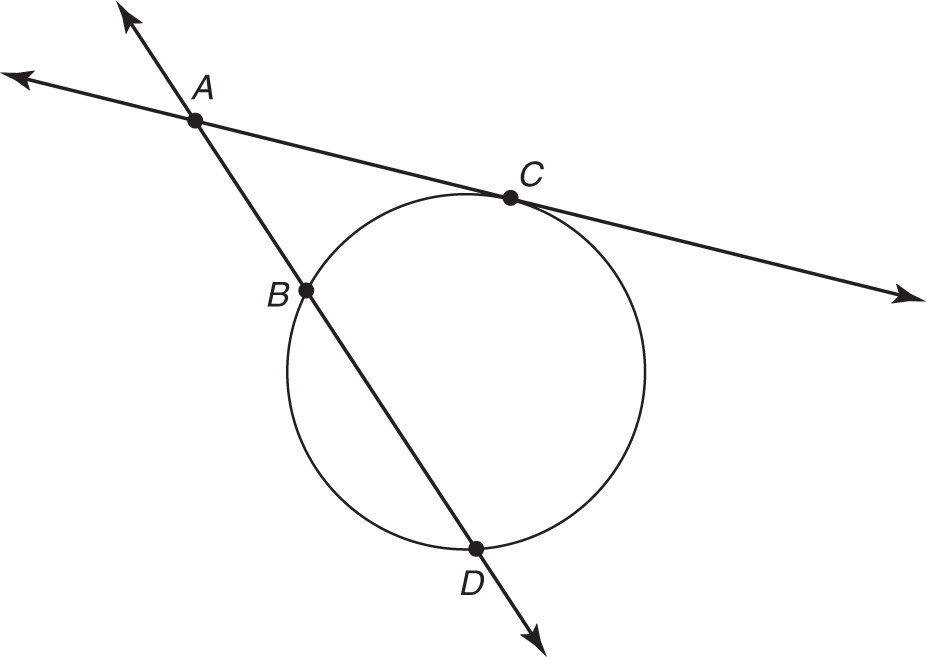
To find the measure on an angle formed by a tangent and a secant that intersect outside the circle, follow the following three steps.
Step 1:Find the measure of both arcs.
Step 2:Subtract the measure of the smaller arc from the measure of the larger arc.
Step 3:Take half the difference.
EXAMPLE:
Find the measure of angle BAC if the measure of arc
BC = 80 degrees, and the measure of arc BD = 100 degrees.
Measure of angle BAC = 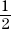(measure of arc CD – measure of arc BC)
Step 1:Find the measure of both arcs. Arc BC = 80. Since there are 360 degrees in a circle, arc CD = 360 – (100 + 80) = 180.
Step 2:Subtract the measure of arc BC from the measure of arc CD.
180 – 80 = 100
Step 3:Take half the difference.
Angle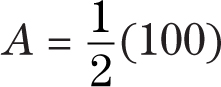 
Angle A = 50 degrees.
Case V: One tangent and one secant
A tangent and a secant can form an angle by intersecting outside the circle, but they can also intersect the circle at the point of tangency. If a tangent and a secant intersect at the point of tangency, two angles are formed. The measure of each angle is equal to half the measure of the intersected arc.
Tangent DE and secant BA intersect at point A. Two angles are formed: angle BAD and angle BAE.
Angle BAD = the measure of arc AB
Angle BAE = 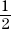the measure of arc BCA
To find the measure of each of the two angles, follow these two steps.
Step 1:Find the measure of both of the intersected arcs.
Step 2:Take half of the measure of each of the intersected arcs.
EXAMPLE:
Find the measure of angle BAD and the measure of angle BAE if the measure of arc AB = 100 degrees.
Step 1:Find the measure of arc AB and arc ACB.
Arc AB = 100
Arc ACB = 360 – 100 = 260
Step 2:Take half the measure of each of the intersected arcs.
Angle BAD = 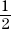(100) = 50 degrees
Angle BAE = 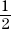(260) = 130 degrees
Case VI: Two secants
Two secants can intersect outside of the circle, inside the circle, or even on the circle. The measure of an angle formed by two secants that intersect outside the circle is half the difference of the measure of the two intersected arcs.
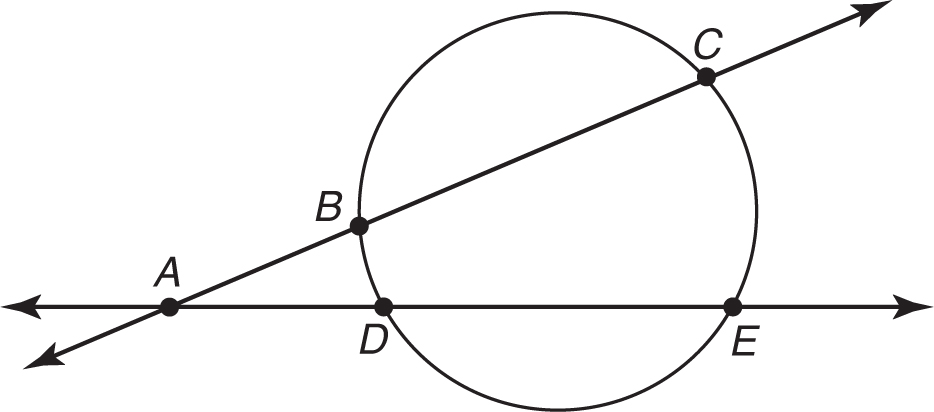
Secants AC and AE intersect each other outside the circle.
The measure of angle CAE = 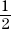(the measure of arc CE – the measure of arc BD).
To find the measure of angle BAD, just follow these three painless steps.
Step 1:Find the measure of both arcs.
Step 2:Subtract the measure of the smaller arc from the measure of the larger arc.
Step 3:Take half the difference.
EXAMPLE:
Find the measure of angle CAE if arc BD = 30 degrees and arc CE = 70 degrees.
Step 1:Find the measure of both arcs.
Arc BD = 30 and arc CE = 70
Step 2:Subtract the measure of the smaller arc from the measure of the larger arc.
Arc CE – arc BD = 70 – 30 = 40
Step 3:Take half the difference.
Angle CAE = 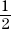(40) = 20
Angle CAE = 20 degrees
Case VII: Two secants
Two secants can also intersect in the interior of a circle. When they do they form two pairs of vertical angles. The measure of each angle is half the sum of the intersected arcs of the angle and its vertical angle.
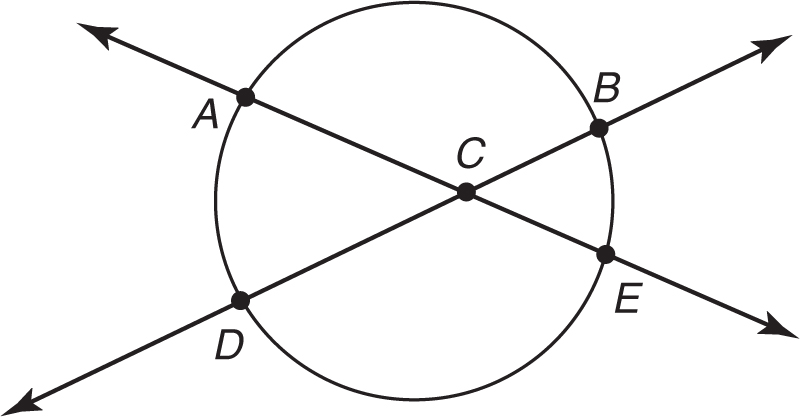
To find the measure of each of the four angles, follow these three painless steps.
Step 1:Find the measure of the arcs of a pair of vertical angles.
Step 2: Take half the sum of the two arcs to find the measure of each of the vertical angles.
Step 3:Subtract the measure of one of the angles from 180 to find the measure of each of the angles in the other pair of vertical angles.
EXAMPLE:
The secants AE and DB intersect each other inside the circle at point C, forming angles ACD, ACB, BCE, and DCE. Find the measures of angles ACD, BCE, ACB and DCE, if the measure of arc AD = 60 degrees and arc BE = 40 degrees.
Step 1:Find the measure of the arcs of two vertical angles.
Arc AD = 60 and arc BE = 40
Step 2:Take half the sum of the two arcs to find the measure of each of the vertical angles.
Angle ACD = 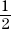(60 + 40)
Angle ACD = 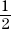(100)
Angle ACD = 50
Angle BCE = Angle ACD since they are vertical angles.
Angle BCE = 50 degrees.
Step 3:Subtract the measure of one of the angles from 180 to find the measure of each of the angles of the other pair of vertical angles.
Angle ACB = 180 – 50 = 130
Angle DCE = Angle ACB = 130 degrees.
Case VIII: A tangent and a radius of a circle
A tangent intersects a circle at precisely one point. Only one radius intersects the tangent at that point, forming two right angles. The vertex of each of these angles lies on the circle.
EXAMPLE:
Tangent AB intersects radius CD at point D. AB is perpendicular to CD.
Angle ADC = 90 degrees and angle BDC = 90 degrees
Summary
There are eight possible cases of angles associated with circles.
Angle formed by |
Location |
Angle Measure Equals |
Two radii |
Interior of the circle |
= the measure of the intersected arc |
Two chords |
On the circle |
= half the measure of the intersected arc |
Two tangents |
Exterior of the circle |
= half the difference of the two intersected arcs |
One tangent and one secant |
Exterior of the circle |
= half the difference of the intersected arcs |
One tangent and one secant |
On the circle |
the measure of the intersected arc |
Two secants |
Exterior of the circle |
= half the difference of the two intersected arcs |
Two secants |
Interior of the circle |
= half the sum of the intersected arcs of the angle and its vertical angle |
A tangent and a radius |
On the circle |
= 90 degrees |
Arc BE = 60 degrees
Arc AD = 60 degrees
C is the center of the circle.
1.What is the measure of angle CBF?
2.What is the measure of angle BFA?
3.What is the measure of angle BCE?
4.What is the measure of angle BCA?
5.What is the measure of angle AED?
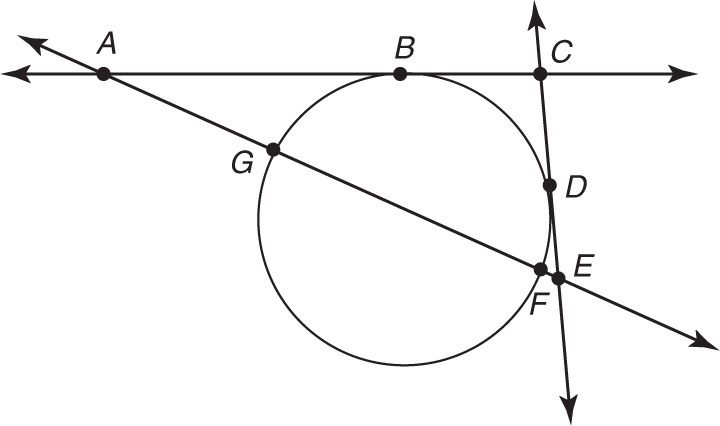
Arc BD = 90 degrees
Arc BG = 70 degrees
Arc DF = 50 degrees
6.What is the measure of angle ACE?
7.What is the measure of angle CEA?
8.What is the measure of angle CAE?
(Answers)
1.What is the area of a circle with diameter 12?
2.What is the circumference of a circle with radius 4?
3.What is the circumference of a circle with area 9π?
4.What is the area of a circle with circumference 10π?
5.What is the length of a 60-degree arc on a circle with radius 12?
(Answers)
