Gravity, mass and the enigma of relativity
Because of gravity, of course. Everybody knows that. However, what is the fundamental nature of gravity? That is a much harder to question to answer, despite the fact that gravity is the first of nature’s fundamental forces to penetrate your consciousness.
Here’s an experiment you can try at home. You’ll need a six-month-old baby (you could borrow one). Tie a piece of fishing line to one of the baby’s toys—a rattle, say. Now suspend it from the ceiling at a height where it will rest lightly on a chair with the line taut and invisible. Get the baby to watch as you whip the chair away. Keep your eyes on the baby’s: when, for no obvious reason, the rattle doesn’t fall to the ground, the baby will stare at it for much longer than is normal.
This, according to psychologists, is how babies express astonishment. It seems that we know from a surprisingly young age that things are meant to fall downward when unsupported, and we are mystified if they don’t. No wonder the levitation tricks of the Victorian illusionists entranced an entire generation. When things cheat gravity, our very core takes delighted offense.
Gravity, you see, is a tyrant. It cannot be cheated. We cannot, as we can with an electric or magnetic field, block it out. Neither can we counter it with an opposing force—there seems to be nothing in physics that equips us with antigravity. The rule of gravity is so central to human experience that we have become, essentially, oblivious to gravity’s presence. It is only in its absence—or, rather, its apparent absence—that we remember it is always there.
Perhaps that is why the earliest ventures into science largely ignored gravity. As we understand it now, one type of action governs the fall of a tripping human, the arc of an arrow’s flight and the motion of the planets, but Aristotle’s textbook Physics makes no mention of any universal force orchestrating the universe. He did suggest that objects did not fall off the Earth because of the Earth’s “heaviness,” but his reasoning was askew. He suggested that the strength of the Earth’s pull depended on how big an object was and what it was made of.
In Aristotle’s view, heavy objects fall more quickly than light objects. That is because of the Greek obsession with the elements: Earth, Air, Fire and Water; most of the heavy objects Aristotle knew about were made from materials found in the Earth, and the strong pull, he said, was because they were compelled to return there. Our understanding didn’t really move on from this flawed idea for almost 2,000 years. Eventually, though, the Italian scientist Galileo Galilei established that Aristotle was wrong: heavy objects are not more strongly attracted by the Earth. As long as air resistance is not a factor, a heavy and a light object will fall at the same rate.
Sadly, the romantic stories about Galileo’s proof of this—by dropping cannonballs from the leaning tower of Pisa—are not true (the myth was started by Galileo’s student Vincenzo Viviani), but it has nevertheless been proved in an even more spectacular fashion. In 1971, Apollo 15 astronaut David Scott paid tribute to the discovery’s profound consequences by dropping a hammer and a falcon feather onto the moon’s surface. “One of the reasons we got here today, was because of a gentleman called Galileo,” Scott said as he let them fall. The hammer and the feather landed, of course, at the same time.
Scott’s appraisal was almost correct: astonishingly, it really didn’t take much more than Galileo’s 17th-century insights to get us to the moon. The gaps were filled by a man born just one year after Galileo died: Isaac Newton. Unimpressive as he was at birth—his mother said he could be “put in a quart mug”—Newton took just a couple of dozen years to gather all the information it would take to plot a course for the Apollo astronauts four centuries later. And here, of course, is where the apple comes in.
Unlike the stories of Galileo’s experiments on the leaning tower of Pisa, accounts of Newton’s gravitational epiphany at the sight of a falling apple are almost certainly true. It was late summer, 1666, and Newton was sat in his garden at Woolsthorpe Manor in Lincolnshire. The apple tree is still there, and still bearing fruit every autumn.
An apple falls because it has a property called mass, and so does the Earth. Newton’s great leap forward was to spell out how everything with mass attracts everything else with mass. His universal law of gravitation, constructed at the tender age of 23, said that the attractive force is dependent on those two masses, the distance between them, and a constant known as G.
Actually, physicists are often over-familiar with the gravitational constant and call it “Big G” to distinguish it from (little) g, the acceleration due to the Earth’s gravitational pull. However, despite the familiarity, G is actually the least well defined of all the fundamental constants.
The size of G, like that of all the other fundamental constants, is known not through some theoretical argument, but through measurement. The English physicist Henry Cavendish was the first to measure it, in 1798, by analyzing the gravitational attraction between two known masses that were a known distance apart. His answer for G was 6.754 × 10–11 meters cubed per kilogram per second squared. Today, G is officially 6.67428 × 10–11 m3/kg/s2. The uncertainty on this measurement is about one part in 10,000. Compare that to the precision with which we know the other fundamental numbers, such as the Planck constant used in quantum theory: that is known to 2.5 parts in 100 million.
There are two reasons G is so difficult to measure accurately. The first is that it is impossible to screen out gravitational fields using any known physics. That means any measurements have to take into account the influence of any and all objects in the vicinity. This makes the measurements unreasonably sensitive to external influence; there are stories of researchers having to recalibrate their apparatus after someone two laboratories away has moved a large pile of books into their office. For this reason, gravity measurements have to be done in isolated laboratories using extraordinarily sensitive instruments.
The second difficulty with measuring the gravitational constant is the fact that gravity is the weakest of the fundamental forces. When that apple falls to the ground, it does so with relatively little acceleration, despite the fact that the mass of the entire planet is tugging it downward.
If you’re not convinced that gravity is weak—maybe you’ve done a parachute jump or been on a rollercoaster and experienced a terrifying acceleration—think about the magnets sitting happily on the door of your refrigerator. The mass of the entire planet is working to pull them toward the ground too—and yet a button-sized dot of magnetized iron can resist the planet’s pull. Magnetism results from the electromagnetic interaction between charged particles inside a magnet. And that force is around 1042—that is, around 1 million trillion trillion trillion—times larger than the gravitational force between them. So gravity is weak: G is astonishingly small. But why? Though the weakness of gravity is one of the central mysteries of physics, we do have some ideas that might account for it. The best is that gravity “leaks” into or out of our universe.
Various branches of modern physics suggest that there are many more dimensions of space than the three (up and down, side to side and backward and forward) that we are familiar with. One of the consequences of this is that certain forces can become “diluted” through spreading into these extra dimensions. If the gravitational force is weak, that may be because it is spread more thinly than the others.
The “extra” dimensions are thought to be “compactified”—rolled up, essentially—so small we don’t experience them in day-to-day life. It’s just a theory at the moment, but a few researchers are trying to find evidence for this. One route is through examinations of the way the gravitational attraction between two objects changes with the distance between them.
“One of the reasons we got here today, was because of a gentleman called Galileo.”
DAVID SCOTT
Newton showed that gravity follows an “inverse square law.” That means that the gravitational force one object exerts on another decreases in proportion to the square of the distance between them. Separate two objects by a meter, and measure the gravitational force. Then separate them by a further two meters and measure the attraction again. It will be nine times weaker because they are three times further away.
The hidden dimensions enter our world at submillimeter scales. If gravity behaves differently from normal on these very small scales—if the inverse square law doesn’t hold when masses are separated by only a few thousandths of a millimeter—that may be because these dimensions are interfering with things. Spot some disturbance here, then, and we might have evidence to support our most daring theories.
This is why physicists are carrying out the most exquisite experiments to probe gravity at microscopic scales. So far, however, they have found no evidence of violations of the inverse square law. That’s a great shame, because one of the roles of these advanced, multidimensional theories is to improve our best theory of gravity, Einstein’s relativity.
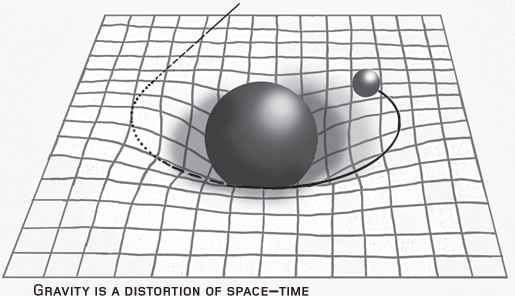
Einstein’s theory of relativity cast space and time as a four-dimensional fabric and said the presence of mass or energy distorted this fabric. Where Newton had declared that bodies in motion will move in a straight line unless acted on by a force, Einstein added a twist. Yes, they moved in a straight line through space, but would have to follow any distortions in that space.
The distortion that the sun’s mass creates, for instance, means that a nearby planet in motion will be pulled into a curved trajectory. Balance the masses and the speed of motion, and you have an orbit. Hence, in Einstein’s view, gravity is a kind of illusion. Though it looks like a force that acts across space and time, it is actually more like topographical features—hills and valleys—added to the landscape, features that make it hard to travel in certain directions, and easier to travel in others.
Neat though this is, and supported by numerous experimental findings, we know it is not the final answer. In a way, Einstein has only given us a clever description of how gravity works. The why is still wide open. There is hope, though. Relativity, in its current form, is not compatible with quantum theory. We will have to wait for some future “quantum gravity” theory to unite the two. And that theory, presumably, will give us the why of gravity, just as we have recently got to grips with the why of mass.

So far, we have been blithely talking about mass, while avoiding the obvious question. What does it mean that something has mass?
Physicists categorize mass in two distinct ways. One is “gravitational mass,” which is what produces and responds to gravitational fields. This is what makes the apple fall. The other is “inertial mass,” which is a measure of how hard it is to move something out of its current state of motion or rest. When you try to push a broken-down car, its inertial mass stands against you.
As far as we know, inertial and gravitational mass are entirely equivalent. Imagine standing on Earth in a sealed box like a stationary elevator. You feel the push of the floor as your gravitational mass responds to the influence of gravity. Now imagine taking that elevator box into space, away from gravitational fields, and sticking a rocket engine on it that accelerates it at 9.81 meters per second per second, the acceleration due to gravity at the Earth’s surface.
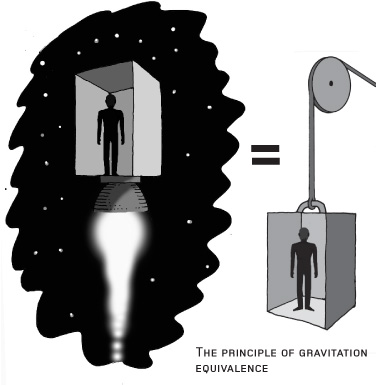
There will be no difference in what you feel, Einstein says. This “equivalence principle,” which says there is no distinction between your gravitational mass and your inertial mass, is part of the bedrock of Einstein’s general relativity. Although we don’t have a definitive proof that it is absolutely correct, experiments have shown this is certainly true to at least one part in 1012. A decade before he created general relativity, though, Einstein asked another question about mass. In 1905, his “miracle year” when he also published his special theory of relativity, Einstein came up with an interesting line of inquiry. He asked, in a landmark paper, whether the inertia of a body depends upon its energy content.
This was the origin of the world’s most famous equation: E = mc2 (see Why Does E = mc2?). Energy and mass, in Einstein’s view, could be interchanged. It took almost a century, but we now know through this equation that energy is indeed the root of mass. Take that apple, for instance. Its mass resides in its constituent components. Going down in scale, these are molecules, which are composed of atoms, which are composed of electrons, protons and neutrons.
The origin of the mass of the electron (which is only one-thousandth the mass of the proton and neutron) remains a mystery. But physicists are at least getting to grips with the mass of protons and neutrons. These particles are each composed of three particles called quarks. However, the masses of the quarks account for only around 1 percent of the proton or neutron mass. The rest comes from a shadowy, quantum world of energy-stealing “virtual particles.”
Down at the quantum scale, the rules are very different from those that we encounter in our day-to-day lives. Here, a phenomenon called the “Heisenberg uncertainty principle” holds sway, and issues strange declarations. One is that nothing has a definite amount of energy, even when that energy is zero. Instead the energy fluctuates around zero, allowing seemingly empty space—something physicists call the “vacuum”—to fizz with appearing and disappearing particles.
These particles appear in pairs: a particle and its antiparticle, spontaneously created as the energy of the vacuum of empty space fluctuates around zero. According to a Nobel Prize-winning branch of physics called “quantum chromodynamics” (QCD), the particles can appear with various amounts of energy, giving a spectrum of characteristics. Sometimes they take a form where they are known to physicists as “gluons.” Gluons create a force known as the strong nuclear force, which holds quarks together to create a proton or a neutron. And it is gluons—or rather their energy—that give the apple most of its mass. Working out exactly how much mass comes from the energy of all these virtual particles has not been easy, involving crunching combinations of around 10,000 trillion numbers. When the results came out, though, they were within a couple of percent of the experimentally recorded masses of these particles.
The energy associated with the gluons, converted via Einstein’s E = mc2 formula, accounts for almost all the mass in a proton or neutron. There is a little missing: the mysterious electron mass, and a contribution from some more virtual particles, such as pairs of virtual quarks and antiquarks, and the Higgs boson (see What is the God Particle?). Essentially, though, the mass of the apple—and of the Earth—is a manifestation of the energy contained in the vacuum of empty space.
The success of quantum chromodynamics in establishing the origin of mass has given physicists hope that similar ideas will eventually lead us to the final why of gravity: the graviton. The electric and magnetic forces are manifest through atoms exchanging of packets of energy called photons. The strong nuclear force comes via gluons, as we have seen. The weak nuclear force is known to result from the exchange of energy-laden particles known as the W and Z bosons. All of these have been seen in experiments. Gravity is thought to rely on the exchange of particles known as “gravitons.” These, however, remain hypothetical. Despite all our advances in understanding, we still haven’t seen a graviton.
That is not our only remaining problem with gravity, however—a much more embarrassing and basic issue remains unsolved. Bizarre as it may seem, although we have worked out the origin of mass using the most ingenious minds, the biggest computers and the greatest theories of physics, we still don’t have a good way to measure the very thing that gravity acts upon: mass. Every other standard unit of measurement has a precise, atomic foundation. The second is based on a certain number of oscillations of a cesium atom. The meter is the distance light travels in a particular fraction of that second. The kilogram, though, is the mass of a lump of metal kept locked inside a Paris vault.
It’s not any old vault, of course: it is contained within the hallowed walls of the International Bureau of Weights and Measures (BIPM) near Paris. And it’s not any old metal, either: it is a cylinder of platinum, chosen as the most stable, incorruptible material available. The mass of this platinum cylinder is the kilogram against which all other kilograms are calibrated. The problem is, its mass is changing. Metrologists have made dozens of copies, and the original no longer weighs the same. There is about 100 micrograms of difference, roughly equivalent to the mass of a couple of grains of salt. Researchers are planning ways to bring the kilogram into line with other standards, by using atomic measurements. One hope is to create a polished sphere of silicon containing a determinable number of atoms. The kilogram will then be defined as the mass of a certain number of silicon atoms.
Another possibility is to use something called a Watt balance to measure mass in terms of energy. Einstein told us that mass and energy are interchangeable; the Watt balance would invoke this by measuring mass against the energy contained in a carefully configured electromagnetic field. Until these plans come to fruition, though, we are stuck with plugging slightly inaccurate numbers into Newton’s formula.
Gravity is everything to us—it pulled particles together to create the Earth, it holds us in orbit around our life-giving sun, it creates the tides that allowed that life to form and move on to land. And now we return the favor and use our gravity-given minds to make extraordinary discoveries about the very nature of this attraction. At the same time, though, we have only primitive tools to get the measure of it. While we can talk about gluons inside the nuclear structure of the atoms within the apple, we cannot be precise about how much the apple weighs. The essence of gravity remains deliciously difficult to tame.