The equation that underpins the universe
Go on, think of an equation. Given all those years of education, whether you enjoyed or endured them, you might think that an equation you learned at school would come to mind. But it doesn’t. Instead, this one, which you probably learned by accident, pops into your head.
It is the most famous equation in the world. It appeared on the cover of Time magazine in 1946, and has since become part of our culture, inspiring artists and musicians, writers and film-makers. It litters the globe: you’ll find it on the logo of a Japanese graphics company, a public relations company in rural England and a Toronto hair salon. Why? Because this equation summarizes how the modern world took its form.
Though the equation, written down by Einstein in 1905, was forty years old before the world saw what it could do, we shuddered at the discovery. On the cover of Time, it is written into a mushroom cloud looming over a fire-struck Pacific atoll. E = mc2 is the equation behind the atomic bomb. It ended the Second World War, and ushered in the age of nuclear power and nuclear threat. With it came the Cold War and, for the first time, the specter of total destruction for the human race. Even now, with the Cold War over, the possibility that the wrong person may learn how to convert a tiny mass into an enormous amount of energy hangs heavy over us.
The happier truth, though, is that E = mc2 is so much more powerful than a bomb. It is the very root of our life, our continued existence and perhaps our future too. It describes the fundamental nature of reality, revealing just how deep the illusion of the familiar notion of matter goes. If there is only one equation in your head, at least it is the right one.

So where did this equation come from? To be strictly accurate, not, at first, from Einstein. In the paper suggesting this relation between mass and energy, Einstein didn’t actually write down E = mc2. He wrote down L = mv2, where L is the “living” energy, m is mass, and v is velocity. It was seven years later, in 1912, that he began to routinely use E for energy, and c for celeritas, the Latin for “swiftness” and a universally acknowledged symbol for the speed of light. Even ignoring the switch of symbols, Einstein didn’t pluck the equation out of the air. The seeds of E = mc2 were sown in laws of physics that were first formulated in the 17th century, then debated for almost two centuries.
The word “energy” has a long history, but we have only recently begun to use it in connection with what we mean by energy today. The Encyclopaedia Britannica of 1842, for example, defined energy as “a term of Greek origin, signifying the power, virtue, or efficacy of a thing.” That Greek origin, which lies with Aristotle, is actually somewhat closer to the mark. Aristotle defined energy as the source of every thing’s being and function. “Energeia,” he said, was what allowed something to do its job.
In Isaac Newton’s day, though, energy was still poorly defined. The concept was there: things that moved—an arrow fired from a bow, for example—had energy. When that arrow landed, however, the energy seemed to be lost. The same happened if two people collided in the street, knocking each other to the floor. Their energies, according to Newton, canceled each other out. Before the collision there was energy; after, there was none.
Fortunately for us—according to Newton, at least—God was there. Newton felt that God, as a living and immanent deity, must be at work somewhere in the universe. One of the deity’s vital roles, Newton suggested, was to top up the cosmic energy reserves. God was there to wind up the clockwork universe and keep the planets moving through the heavens, but he also applied himself to everyday situations—to colliding peasants, for example.
“He had not, it seems, sufficient foresight to make it a perpetual motion.”
GOTTFRIED LEIBNIZ
It was not a view shared by Newton’s great rival, the atheist Gottfried Leibniz. In an acerbic comment on Newton’s view, Leibniz said he found it hard to understand that God Almighty would have to wind up his own watch from time to time. “He had not, it seems, sufficient foresight to make it a perpetual motion,” Leibniz wrote in a 1715 letter to the philosopher Samuel Clarke. Newton and Leibniz were already rivals over the authorship of the mathematical tool known as calculus, which had enabled Newton to calculate the orbital motions of the planets. This conflict over energy, too, could be boiled down to another mathematical issue.
Newton had formulated the energy of a moving body as mv, the product of its mass m and velocity v. Leibniz, on the other hand, thought it to be mv2, the product of the mass and the square of its velocity. The difference had a profound effect. In Newton’s formulation, two identical bodies moving in the opposite direction with the same velocity would have energies mv and –mv.. If they collided, the resulting energy would be zero. Leibniz’s squaring of the velocity meant that the “negative” direction made no difference, because a negative quantity always squares to a positive number. In Leibniz’s formulation, the energy was not lost from the universe.
For a number of years, the question was simply a matter of ideology. If you were English-speaking, you liked Newton’s work and ideas, you thought of energy as mv. If you spoke German, you sided with Leibniz, and squared the velocity. This jingoism was overcome through a Dutch and French collaboration. Willem ’s Gravesande, a Dutch scientist, had been dropping weights into soft clay from various heights. The depth of the hole the weights made was, presumably, proportional to the energy, which in turn must be proportional to the height from which they were dropped and the speed on impact. The only way the sums worked was if energy was indeed proportional to the square of the velocity. ’s Gravesande didn’t see this for himself. It was a French noblewoman called Emilie du Châtelet who put all the pieces of the puzzle together in the first half of the 18th century and declared Leibniz the winner. The energy due to motion—living, or kinetic energy—was proportional to the square of the velocity. E depends on a velocity squared.
Though ’s Gravesande and (in particular) du Châtelet had made great strides forward in illuminating the relationship between a body’s motion and its energy, they still had no idea what happened to all the energy once the motion had stopped. Did it disappear? The answer to that question only came after the discovery of a principle called “conservation.”
The first experimental hints at a general principle of conservation came in the late 18th century. In an astonishingly careful set of experiments, carried out just a few years before he was guillotined at the behest of the Paris revolutionaries, the French scientist Antoine Lavoisier monitored how a variety of materials changed with burning, rusting, or some other natural process of change. He found their mass was always conserved in some manner.
Each of the experiments was carried out in a closed container, and the substance under investigation (together with any air or water in the chamber) was weighed before and after the experiment. Within the limits of his experiment, the total mass of material in the chamber remained constant. Even something as violent as combustion, which altered the physical form of a material so radically, still did not push materials out of existence. The mass measurements told Lavoisier it remained there in the experimental chamber; altered in form but still there nonetheless. Things didn’t simply disappear from the universe, but they could be transformed between different forms.
That probably comes as no surprise to you. Thanks to a couple of centuries of experiments such as Lavoisier’s, we have come to accept that the universe is, effectively, a “closed” system, containing a finite amount of “stuff” that can be transformed from one state into another. And the most fundamental transformable—but always conserved—quantity is energy.
After taking thousands of years to get to grips with the concept of energy, it still took almost the whole of the 19th century for scientists to work out that energy is always conserved in nature. With hindsight, it seems a little odd that this revelation was so slow in coming. It had long been known that kinetic energy could be converted to heat. Those who bored the barrels of cannons, for example, knew that the process generated vast amounts of heat. But it was only with the invention of thermodynamics, the branch of science that relates temperature and heat to the motion of atoms and molecules (see Why is There No Such Thing as a Free Lunch?), that we discovered exactly how that worked.
If E = mc2 rules the modern world, thermodynamics created it. The discovery that heat was a form of energy, and thus could be converted to kinetic energy that would perform work, was revolutionary in every sense. Heat a bath of water sufficiently, and its conversion to steam—when under pressure—could move a piston. And moving a piston could change the fate of nations. The discovery of machines such as the engine and the refrigerator, powered by mechanical work or heat, created the Industrial Revolution, the foundation of the modern, technological age.
This conversion of heat energy into kinetic energy is just one example of how energy is conserved, moving between multiple forms but never disappearing from the universe. ’s Gravesande’s weights, for example, had “gravitational potential energy” before he dropped them. That potential energy came from the energy, stored in his muscles, used to lift them to the drop height. That energy came from the food he ate, and that, in turn, came from his food’s ultimate energy source: sunlight. When the weights hit the clay, their potential energy, ultimately derived from sunlight, was converted to kinetic energy (or movement) in the clay, some heat energy (due to friction), and sound energy. The energy did not disappear from the universe.
Similarly, a paraffin lamp contains potential energy. When the paraffin burns, the stored chemical potential energy is released as heat and light. The heat energy will be imparted to the molecules in the air around the lamp, and will manifest as kinetic energy: the molecules will move faster.
What seems surprising, though, is that energy can take the form of mass. Mass is surely very different from energy: while mass is associated with solidity, energy seems transient and ephemeral. But there is a link—and it is found in James Clerk Maxwell’s equations of electromagnetism.
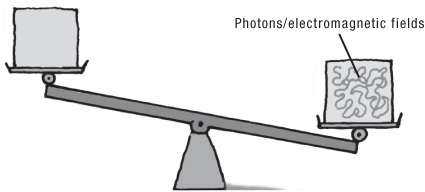
In the 1830s, Michael Faraday showed how electricity and magnetism are interrelated: electricity produces magnetism, and vice-versa. Shortly afterward, Maxwell came up with a series of equations that detailed exactly how this process worked. Many physicists looking into Maxwell’s equations saw that they contained the essence of mass. It was well known, for example, that a box containing electromagnetic fields weighed more than one containing none. The question was, what did that mean?
The mainstream view was that inertial mass—the resistance of a body to movement—lies in the fact that charged particles would be difficult to move in the vicinity of their own electromagnetic fields. True to his character, Einstein did not follow the mainstream. Instead, he found the answer in one of the flaws of the equations.
Maxwell once said that his equations describe a “mutual embrace” between electricity and magnetism. However, it is actually a three-way embrace: electricity and magnetism do not exist without movement; the motion of charged particles creates electricity and magnetism. And herein lay a deep problem. Analysis of experiments showed that motion could invalidate the equations. If the emitter of electromagnetic radiation was moving relative to the observer, the equations no longer predicted the correct values for the electromagnetic field.
This was what motivated Einstein’s 1905 paper “On the Electrodynamics of Moving Bodies,” in which he introduced special relativity. Einstein’s genius was to insist that the laws of physics be consistent however you are moving through space. To do this, he modified Maxwell’s equations so that you couldn’t move in any way that changed the speed of light from its absolute value, c. The speed of light is an unassailable constant. Move toward a stationary source of light, and the light will always come at you with speed c. Move away, and you will measure it passing you at c. And here is where we find the link between energy and mass.
Einstein suggested that the existence of energy—any kind of energy—brings with it an associated mass. As he stated in a letter to his close friend Conrad Habicht, shortly after publication of the E = mc2 paper, “The relativity principle, in association with Maxwell’s fundamental equations, requires that the mass be a direct measure of the energy contained in a body; light carries mass with it.”
The first implication Einstein noted was for radioactivity: if radium was giving out energy, it ought also to lose some mass. The German physicist Max Planck saw a more prosaic (but in some ways more profound) implication. A hot object—a frying pan, say, will weigh more than a cold one. This was a revolutionary idea—even today it still seems strange. Nevertheless, it is absolutely correct. We now have good evidence that mass is just one way of carrying energy. You can move, and carry kinetic energy, but you can also lock your energy in by simply existing. To see why, we need to explore the origin of mass.
You are made of particles that, at their root, have no independent mass. They get their mass from a quantum phenomenon known as the “Heisenberg uncertainty principle.” At root, this says that every quantity in nature has a fuzziness; it doesn’t have a fixed value. That’s true even of the energy of empty space: while we think of it as having zero energy, it is actually fizzing with energy that manifests as pairs of “virtual” particles that disappear as quickly as they appear. These fleeting, ghostly particles, it turns out, give the frying pan its mass.
When you shrink down in scale from frying pan, to iron atom to iron nucleus, you end up looking at particles called quarks, which make up the protons and neutrons in the iron nucleus. When physicists work out the mass of quarks, there is nowhere near enough to account for the heaviness of the pan. The mass actually exists in virtual particles that manifest from the fuzzy energy of empty space. Experiments involving high energy particle collisions and the crunching of millions of numbers have confirmed that these “gluons” act to hold the quarks together in the proton and neutron, and that the energy involved is what we see as most of the mass of the pan.
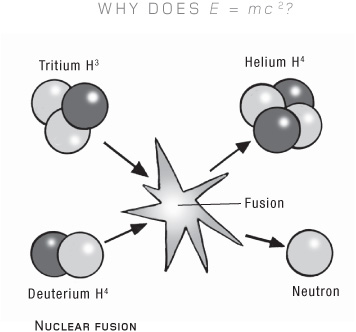
Hence the hot pan weighing more. Given that almost the entire mass of a frying pan comes from the fizzing energy of empty space, it doesn’t seem quite so hard to believe that adding a bit more energy, in the form of heat, also adds to the mass. The ability of high-energy processes to release this energy is what lies at the heart of our existence. When hydrogen atoms fuse in the sun, eventually forming a helium atom, the process releases some of their gluon energy (energy that we call mass) as heat and light—the very heat and light that created life on Earth.
Thanks to the colossal size of the speed of light, coupled with the fact that E = mc2, there is a surprising amount of energy locked up in ordinary matter. A single walnut, for example, has enough potential energy locked within it to power a city. We have released something like this, of course—not with walnuts, but with atoms of uranium. Suitably prepared, their gluon energy can be released to provide electrical power to cities—or to bomb them.
Whether in bombs or in power stations, we have measured the mass of the particles we begin with, the mass at the end of the process, and the amount of energy released. In every case it has been shown to be true: E really does equal mc2. The most accurate proof we have of the validity of Einstein’s equation was carried out in 2005. Unsurprisingly, it involved painfully sensitive measurements. The energy measurement for the left hand side of the equation, for example, required a team of researchers to measure the energy of a gamma ray photon to around one part in 1 million.
For the mass side of the equation, meanwhile, the researchers had to measure how the mass of an ion changes when it gives off a gamma ray photon. That is a tiny change in mass, equivalent to seeing a hair’s breadth change in the distance from New York to Los Angeles. There were no nasty surprises: the researchers found a startling agreement between the two measurements. It seems that E really does equal mc2, to better than one part in 2 million. You can rest easy: that one equation you know is pretty solid.