Uncertainty, quantum reality and the probable role of statistics
We could start by turning the question on its head. Is everything predictable? Can we work out the rules that determine how the processes of the universe occur? That would give us extraordinary power over nature, the kind of power humanity has always dreamed of.
In many ways, the whole of human existence is wrapped up in this quest. We look at the world around us, and attempt to find regularities and correlations that enable us to reduce what we see to a set of rules or generalities. This enables us to make predictions about the things we might or might not encounter in the future, and to adjust our expectations and our movements accordingly. We are, at heart, pattern-seekers.
A facility for pattern-spotting has served us well as a species. It is undoubtedly what enabled us to survive in the savannah. A predator might be camouflaged when still, but as soon as the beast moved, we would spot a change in the patterns in our surroundings, and take evasive action. Roots and berries grow in predictable geographical and temporal patterns (the seasons), enabling us to find and feast on them.
The evidence suggests that, because our lives depended on pattern recognition, the evolution of our brains took the process to extremes, forcing us to see patterns even when they are not there. For example, we over-interpreted the rustles of leaves and bushes as evidence for a world of invisible spirits. Modern research suggests this kind of oversensitivity to patterns in our environment has predisposed us to religious conviction; a tendency toward irrational thinking—the consideration of things we can’t touch, see or account for—is the price the human species has paid for its survival.
Ironically, though, scientists have only been able to draw conclusions about where irrational thinking comes from because of the mote in their own eye. Scientists are now painfully aware of their tendency to see patterns where there are none, and randomness where there is order. In order to combat this, and to determine whether there is any order, purpose or structure in the world around us, we needed the invention that exposes both how brilliant, and how foolish, the human mind can be. You might know it better as statistics.
Unlike many of the developments of modern science, statistics had nothing to do with the Greeks. That is remarkable when you consider how much they enjoyed gambling. The Greeks and Romans spent many hours throwing the ancient world’s dice. These were made from astralagi, the small six-sided bones found in the heels of sheep and deer. Four of the sides were flat, and these were assigned the numbers. Craftsmen carved the numbers one and six into two opposing faces, and three and four into the other two flat faces. The way the numbers were situated made one and six around four times less likely to be thrown than three or four.
An enterprising Greek mathematician, you might think, could have made a fortune in dice games involving astralagi. However, there are reasons why no one did. Firstly the Greeks saw nothing as random chance: everything was in the hidden plans of the gods. Also the Greeks were actually rather clumsy with numbers. Greek mathematics was all to do with shape: they excelled at geometry. Dealing with randomness, however, involves arithmetic and algebra, and here the Greeks had limited abilities.
The invention of algebra was not the only breakthrough required for getting a grip on randomness. Apparently, it also needed the production of “fair” dice that had an equal probability of landing on any of their six faces; the first probability theorems, which appeared in the 17th century alongside Newton’s celestial mechanics, were almost exclusively concerned with what happens when you roll dice.
“Chance, that mysterious, much abused word, should be considered only a veil for our ignorance. It is a phantom which exercises the most absolute empire over the common mind”
ADOLPHE QUETELET
These theorems were predicated on the idea that the dice are fair and, though rather primitive, they laid the foundations for the first attempt to get a handle on whether processes in the natural world could be random. From dice, through coin tosses and card shufflings, we finally got to statistics, probability and the notion of randomness.
The Belgian astronomer and mathematician Adolphe Quetelet first began to apply probability to human affairs in the 1830s, developing statistical notions of probability distributions of the physical and moral characteristics of human populations. It was Quetelet who invented the concept of the “average man.”

When he turned his attention to the notion of randomness in natural events, Quetelet was determined to take no prisoners. “Chance, that mysterious, much abused word, should be considered only a veil for our ignorance,” he said. “It is a phantom which exercises the most absolute empire over the common mind, accustomed to consider events only as isolated, but which is reduced to naught before the philosopher, whose eye embraces a long series of events.”
Though ancient civilizations might have been able to predict the motions of the planets, until Quetelet no one thought that there could be any pattern to the way rain falls on a windowpane or the occurrence of meteor showers. Quetelet changed all that, revealing statistical patterns in things long thought to be random.
Not that the notion of randomness was killed with Quetelet. His work showed that the “long series of events” followed a statistical pattern more often than not. But that left open the idea that a single event could not be predicted. While a series of coin tosses will give a predictable distribution of heads and tails, the outcome of a single coin toss remains unpredictable in Quetelet’s science.
Even here, though, science has now shown perception of randomness to be a result of ignorance. Tossing a coin involves a complicated mix of factors. There is the initial position of the coin, the angular and linear momentum the toss imparts, the distance the coin is allowed to fall, and the air resistance during its flight. If you know all these to a reasonable accuracy, you can predict exactly how the coin will land.
A coin toss is therefore not random at all. More random—but still not truly random—is the throw of a die. Here the same rules apply: in principle, if you know all of the initial conditions and the precise dynamics of the throw, you can calculate which face will end facing upward. The problem here is the role of the die’s sharp corners. When a die’s corner hits the table, the result is chaotic (see Does Chaos Theory Spell Disaster?): the ensuing motion depends sensitively on the exact angle and velocity at which it hits. The result of any subsequent fall on a corner will ultimately depend even more sensitively on those initial conditions. So, while we could reasonably expect to compute the outcome of a coin toss from the pertinent information, our predictions of a die throw will be far less accurate. If the throw involves two or three chaotic collisions with the table, our predictions may turn out to be little better than random.
It is important to make the distinction between chaotic and truly random systems, however. A dice throw is not predictable to us, but neither is it random: we know it follows discernible laws, just not ones whose consequences we can accurately compute given our limited knowledge of the initial circumstances. We can say the same about the weather: it is our limitations—our ignorance, in Quetelet’s words—that make it seem random. So is anything truly random? This is a question that lies at the center of one of the greatest, and most fundamental, debates in science.
At the beginning of the 20th century, Lord Kelvin expressed his delight at the way physics was progressing. Newton had done the groundwork, and his laws of motion could be used to underpin the emerging understanding of the nature of light and heat. Yes, there were a couple of small issues—“two clouds,” as he put it—but essentially physicists were now doing little more than dotting the ‘i’s and crossing the ‘t’s on our understanding of the universe. Coincidentally, the great German mathematician David Hilbert was feeling similarly optimistic. In 1900, at a mathematical congress in Paris, Hilbert set out 23 open mathematical problems that, when solved, would close the book of mathematics.
Both Hilbert and Lord Kelvin were guilty of misplaced optimism. Within a few years, relativity and quantum theory had blown apart the idea of using Newton to formulate the future of physics. What’s more, the Austrian mathematician Kurt Gödel had pulled the rug from under Hilbert’s feet, answering a mathematical question that Hilbert had not even asked—and taking away all certainty that any of Hilbert’s questions could be answered.
Gödel had formulated what he called an incompleteness theorem. It says, essentially, that there are some mathematical problems that can never be answered. Because of the way we formulate mathematical ideas, some things can never be proved. Mathematics is destined to be eternally incomplete. This has deep relevance for the question of randomness. If some things are unknowable, their behavior may be, for all we know, random. Randomness might not actually be an inherent property of the system, but we can never prove that it is not. Gödel published his incompleteness theorem in 1931. By this time, the notion of limits to what we can know was hardly even a surprise. If you were familiar with the newly birthed quantum theory, you were already resigned to your ignorance of the ultimate answers.
First, quantum theory gave us the problem of inherent uncertainty. Werner Heisenberg was the first to notice that, when dealing with the equations of quantum theory, you could ask questions about the characteristics of the system under scrutiny, but there were certain combinations of questions that couldn’t be asked simultaneously. The equations will give you the precise momentum or position of a particle, for instance. But they won’t give you both at the same time. If you want to know the precise momentum of a particle at a particular moment, you can say literally nothing about the position of the particle at the same moment. This, the Heisenberg uncertainty principle, is a fundamental characteristic of quantum theory.
Heisenberg used the analogy of a microscope to justify this. If we want to look at the position of a particle, he said, we have to bounce something off it—a photon of light, in this case. But by so doing the photon imparts momentum to the particle. In other words, by measuring the position, we have introduced a change to a separate characteristic—we cannot simultaneously know the position and the momentum with any accuracy. Any measurement—to determine momentum, or energy, or spin—will have concomitant effects on other characteristics. Certainty about every characteristic of a system at one moment in time can never be achieved.
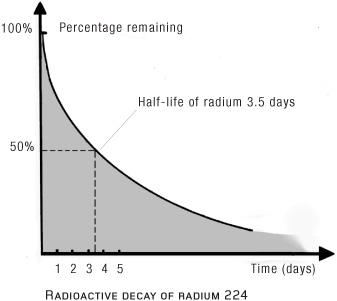
The second even more fundamental problem is not so much one of practical limitations, but straightforward inherent predictability. The classic example for this is a piece of radioactive rock, such as the lump of radium that Marie Curie carried around with her. Physicists can tell you that, if it is composed of the quickest-decaying isotope of radium, the radioactivity of the lump will be halved every three and a half days. After a week, then, it has a quarter of its original radioactivity.
This, however, is a statistical average. It tells you nothing about whether any particular atom of radium will decay in a given time. After 1,000 years, some of the atoms in that lump will still not have decayed. Some will decay in minutes of you starting your clock. And there is no way to predict which is which. Nothing in quantum theory tells us what prompts the decay. It is, to all intents and purposes, random, as if the Almighty rolls ten dice for each atom and only a set of ten sixes causes decay. Einstein took this as proof that quantum theory is incomplete. There must, he said, be some “hidden variables” that substitute for this divine dice game.
The idea that the “Great One” does not play dice is perhaps Albert Einstein’s most documented concern. It is worth pointing out that it was not religiously motivated. Einstein often used “God” as a metaphor for nature or the universe. His point is simple and materialistic. Surely the universe runs by deterministic laws? Surely every effect has a cause? Niels Bohr, widely seen as the founding father of quantum theory responded to this with scorn. Quantum theory, he told Einstein repeatedly, is founded on randomness. Some effects have no cause. “Einstein, stop telling God what to do,” he said.
As with Heisenberg’s uncertainty principle, this randomness does seem to be written right into the equations of quantum theory. The central equation, the only way to make sense of experiments carried out on quantum systems, is the Schrödinger wave equation. This assigns quantum objects the characteristics of waves. If we want to know something about the quantum world, we solve this wave equation. All we get out of it, though, is a probability.
This is really what sets quantum theory apart. By the time quantum theory was born, in the 1920s, statistics was a firmly established discipline of science. Thermodynamics, the study of heat that had partnered the Industrial Revolution, relied upon it. Many other branches of science used statistics to verify the results of experiments. Quantum theory, though, seemed unique—and, to Einstein, disturbing—in its assertions that its results could only be expressed as probabilities.
The results of quantum experiments, according to the orthodox interpretation of quantum theory, were down to pure chance. Einstein’s refusal to accept this is largely to do with the profundity of its implications. Quantum theory describes the world at the scale of its most fundamental particles. If quantum processes are random, then everything is ultimately random.
Bohr had no problem with this because he believed that, ultimately, nothing has any properties at all. Our experiments and measurements, he believed, will produce certain changes in our experimental equipment, and we interpret those in terms of the momentum of an atom, or the spin of an electron. But, ultimately, he said, those qualities are not a reflection of something that exists independently of the measurement. Thus, to Bohr, there was no reason why the results of experiments should not appear randomly distributed; there was no ordered objective reality from which some nonrandom result could arise. To his mind, it would be odd if it were any other way.
It seems an extraordinary point of view: radical and shocking. An electron only exists as some quirk of our measuring apparatus. Small wonder that the infinitely more “common sense” oriented Einstein debated this with Bohr for decades. Einstein said he “felt something like love” for Bohr when it began, such was the intensity and pleasure of their intellectual jousting. However, by the end, it had reached the point where the pair had nothing to say to one another. One dinner given in Einstein’s honor saw Einstein and his friends huddled at one end of the hall, while Bohr and his admirers stood at the other.
Ultimately, history has decided that Bohr was right. Perhaps that is inevitable, given the force of Bohr’s personality—he did once reduce Werner Heisenberg to tears, for instance. Whatever the truth, while Einstein’s notion of a set of hidden variables that are waiting to be discovered remains scientifically respectable, the mainstream view is that objective reality does not have any independent existence. All we can say about the reality that manifests in quantum experiments is that we can predict the spectrum of possibilities, and how likely each one is to be seen. So, is that the last word? Is the universe ultimately random? Are we, as creatures composed of quantum molecules, doomed to find ourselves at the mercy of capricious forces? Yes—but the question is loaded like a Roman die.
We naturally seem to phrase randomness in negative terms, talking about suffering “the slings and arrows of outrageous fortune.” But, as Shakespeare well knew, luck is often kind too. He has Pisanio declare in Cymbeline, for example, that “fortune brings in some boats that are not steered.” The problem is, millennia of religious thought has imposed a sense that everything that happens in the world around us happens for a reason. Science has reinforced this: we appreciate predictability. But randomness can be useful too (see box: More Than Noise).
What’s more, it may even be at the root of our very existence. The Heisenberg uncertainty principle is, as we have seen, fundamental to the universe. One of the consequences of this is that even regions of empty space cannot have zero energy; instead, all of space is populated by a frothing of “virtual” particles that pop in and out of existence at random. These quantum fluctuations in the “vacuum” of space are thought to be the source of the “dark energy” that is driving the accelerating expansion of the universe. A similar kind of fluctuation that came “out of nothing,” but grew rather than disappeared again, is the best explanation we have for the cause of the Big Bang that gave rise to our universe. You might think randomness is a bad thing, but without it you wouldn’t be here to think at all.