RELATIVISTIC COSMOLOGY

If Edwin Hubble had gone no further than his convincing demonstration that the universe extended far beyond the Milky Way and that many galaxies of stars exist besides our own, his name would have been etched in history. Instead he had it etched a second time when he provided evidence that most galaxies are moving away from Earth at speeds that increase linearly (at least as indicated by the best data of the time) with their distances.

As far back as 1912, Vesto Slipher had used the shifts of spectral lines to infer that spiral nebulae are speeding away from us, or, in the case of Andromeda, toward us, at enormous speeds. While this was not direct proof of their extragalactic nature, it was at least an early indication that the universe extended beyond the Milky Way.

It was at this point that observation and theory began to gel as a common unit, although few theorists knew anything about data and few observers knew anything about theory. As we saw in chapter 6, Einstein added a term to his gravitational equation, called the cosmological constant, to provide a repulsive gravity. He felt the term was needed to stabilize the universe; otherwise, all the stars would collapse onto one another.

In 1917, Einstein was able to come up with a solution to his equation in which the universe was a spatially finite (closed), static, four-dimensional hypersphere.¹ This is sometimes called the “cylindrical universe” since when you suppress one of the spatial axes, the universe at any given time is a circle and when you add the time dimension, it is a cylinder in space-time (see figure 8.1).

It should be noted that while Einstein's solution was technically static, it was unstable, like a rock sitting on top of a mountain peak. Any slight change in one of the parameters of the model, such as the cosmological constant or matter density, would result in the universe expanding forever or collapsing in a big crunch.

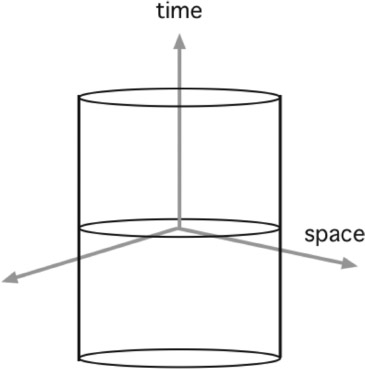
Figure 8.1. Einstein's static universe. A hypersphere in four dimensions, shown with one spatial dimension suppressed so it appears as a cylinder. It has no beginning or end. Image by the author.

Also in 1917, Dutch astronomer Willem de Sitter (1872–1934) showed that another static cosmological solution of Einstein's equation existed in which the universe is empty of matter, containing only the energy implicit in the cosmological constant.² It is illustrated in figure 8.2. In Einstein's solution, the gravitation attraction of the mass of the universe is exactly balanced by the repulsion of the cosmological constant. In the de Sitter solution, there is no matter or radiation—just a constant, positive curvature of space given by the cosmological constant and a gravitational repulsion that causes the universe to expand exponentially.

Of course, you will say that an expanding universe is not “static.” De Sitter's universe is called static since it always expands at the same exponential rate and always will. In this model, the energy density is constant as the universe expands so the total internal energy increases with time. This does not violate energy conservation since the internal pressure corresponding to the cosmological constant is negative. Viewed as a thermodynamic system, it does work on itself.

In the diagram shown in figure 8.2, the de Sitter universe has no beginning or end. The line below the vertex represents the ever-decreasing diameter of the cone as you go in the negative-time direction. However, as we will see later it has since been proven that inflationary expansion must have a beginning, although that beginning can have been preceded by a prior contraction.

Einstein was not happy with the de Sitter solution. Besides, the universe is not empty.³ De Sitter suggested that his solution might be a good approximation if the matter density is low. As we will see, he was not far off. Our universe is only about 26 percent matter and negligible radiation, as measured by energy or mass density. (In chapter 10 we will clarify the distinction cosmologists make between matter and radiation.)

FRIEDMANN'S UNIVERSE

In 1922, Russian physicist and mathematician Alexander Friedmann showed that space and time do not necessarily comprise a static manifold but can also constitute a dynamic one. Rather than presenting his original formulation, I will use the current conventional way to describe Friedmann's concept.

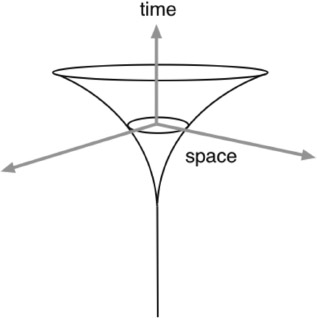
Figure 8.2. The de Sitter universe with one space dimension suppressed. The universe is an exponentially expanding sphere empty of matter. It has a positive cosmological constant that is equivalent to a constant energy density. Image by the author.

In 1929, American physicist Howard Robertson wrote a definitive paper, “On the Foundations of Relativistic Cosmology,” that introduced what is now called the Robertson-Walker metric, also derived by Arthur Walker in 1935, that specifies all the possible line elements in four-dimensional space-time for a homogeneous, isotropic universe. He showed that the Einstein and de Sitter solutions are the only ones that are static and Friedmann's equations provided for all general, dynamic solutions.4

Working from Einstein's gravitational equation, Friedmann derived two new equations describing how the universe can evolve with time.⁵ Assuming a homogeneous and isotropic universe, Friedmann's equations allow one to calculate the time-dependence of a quantity a(t), called the scale factor in the Robertson-Walker metric, which describes how space expands or contracts.

Friedmann's concept is often described in popular terms as an expanding balloon. Paint two spots on the surface of a partially inflated balloon. When you inflate the balloon further, the spots will move apart; if you deflate it, they will move together. In Friedmann's picture, the two-dimensional surface of a three-dimensional balloon is analogous to three-dimensional space in four-dimensional Minkowski space-time.

Friedmann found three possible general scenarios for cosmic evolution depending on a parameter k, called the curvature parameter, which determines the overall geometry of three-dimensional space. If k = 0, space is flat, that is, its geometry is Euclidean. If k = +1, the universe is closed and space is non-Euclidean with positive curvature, like the surface of a three-dimensional sphere. If k = –1, the universe is an open three-dimensional hyperboloid and space has negative curvature, like a saddle. We can think of each of these geometries in terms of the sum of interior angles of a triangle: 180° for k = 0, greater than 180° for k = +1, less than 180° for k = –1.

The specific solutions to Friedmann's equations depend on the nature of matter in the universe and the values of k and the cosmological constant, Λ.

Einstein did not welcome Friedmann's model. He thought he had found a mathematical error in Friedmann's paper, but then admitted it was mathematically correct but had “no physical meaning.” Unfortunately, Friedmann was not able to pursue his work further, dying in 1925 at the young age of thirty-seven. A recent article claims that his contributions to cosmology are not well understood and are often misrepresented.6 Perhaps Friedmann died before he had time to recognize them himself, since he did not connect his calculations to astronomical observations.

LEMAÎTRE'S UNIVERSE

About the only scientist of the time who seemed to grasp the developing connection between mathematical cosmology and the remarkable observations that were coming in at the same time was a Belgian Jesuit priest and physicist, Georges Lemaître. In 1927, Lemaître published an article in French titled, “Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques” (“A Homogeneous Universe of Constant Mass and Growing Radius Accounting for the Radial Velocity of Extragalactic Nebulae”).7 There he showed that Einstein's equation leads to an expanding universe that accounts for galactic redshifts. Lemaître did not cite Friedmann nor mention other cosmological solutions since he was interested in describing what was being observed at the time. Lemaître's formulation is now known as the Friedmann-Lemaître solution.

However, having been written in French and published in a minor journal that few read, Lemaître's paper lay unrecognized for several years. Lemaître himself did not promote it, although he had sent a copy to Eddington, who did not respond.

Just six months after his paper came out, Lemaître met with Einstein in a park in Brussels. Einstein was attending one of the historic Solvay Conferences that were held regularly in Brussels. The fifth conference in 1927 became legendary, having been attended by every physicist who was anybody (Einstein, Bohr, Planck, Schrödinger, Heisenberg, Born, Pauli, Dirac, Lorentz, Perrin, de Broglie, Rutherford, Jeans, Poincaré, Brillouin, and so on…) and featuring the beginning of the momentous debate on quantum mechanics between Einstein and Bohr that continued for years.⁸ Seventeen of the twenty-nine attendees were or would become Nobel Prize winners.⁹ (No astronomers were included).

In the park, Lemaître, who was also not invited, briefly explained his model to Einstein, who replied, “Your calculations are correct, but your physical insight is abominable.”¹⁰

HUBBLE'S LAW

In the meantime, Hubble and his capable, meticulous assistant, Milton Humason (1891–1972) were working away. Neither knew much about general relativity. What they knew was how to observe the skies. Humason had an eighth-grade education at the time (he eventually earned a doctor of science degree) and learned how to make astronomical observations after driving mule trains of supplies up the mountain. At Hubble's request, Humason spent long, cold, boring nights at the 100-inch telescope, taking long-exposure spectrographs of faint galaxies.11 In that day before computers, the observer had to sit high up in a small cage near the mirror's focal point, open to the cold outside air, peering through a viewer at the object of interest, constantly adjusting the mirror manually as Earth rotated so that the object stayed in the crosshairs.

In 1929, Hubble published a seminal paper in the Proceedings of the National Academy of Sciences titled “A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae.”¹² There he proposed what became known as Hubble's law: the radial velocity of a galaxy is proportional to its distance. Humason was not left out. He authored the paper just preceding Hubble's in which he reported that the elliptical galaxy NGC 7619 was traveling away from Earth at 3,779 kilometers per second, twice as fast as any previous measurement and over a hundred times faster than Earth's orbital speed around the sun.¹³

Hubble's paper presents the graph shown in figure 8.3, which plots radial velocities of galaxies against their distances. Although the scatter of points is large, a clear trend can be seen for the more-distant nebula to be moving away from us as higher speeds, as expected if the universe is expanding. This was not a surprise; others had already noticed this tendency. However, Hubble now had the conclusive evidence. As for the fit to a straight line, that's hardly demonstrated, but, with the given data, it's the best you can do.

The caption in figure 8.3 is quoted exactly from the paper. The velocity axis on the graph is mislabeled and should be kilometers per second. The distance axis is in parsecs, where one parsec equals 3.26 light-years.¹⁴

While most of the velocities plotted are positive, a few negative points indicate some closer galaxies, such as Andromeda, moving toward us. The distances to most of the galaxies in Hubble's sample were not determined by Cepheids, which were too faint, but by the brightest stars or the luminosity of the galaxy as a whole.

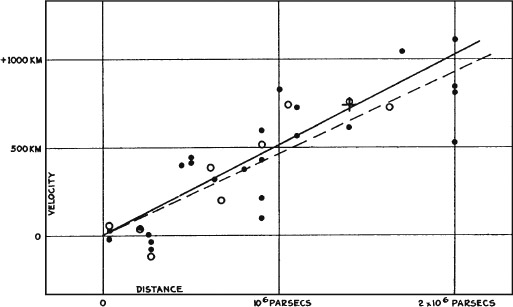
Figure 8.3. “Velocity-Distance Relation among Extra-Galactic Nebulae. Radial velocities, corrected for solar motion, are plotted against distances estimated from involved stars and mean luminosities of nebulae in a cluster. The black discs and full line represent the solution for solar motion using the nebulae individually; the circles and broken line represent the solution combining the nebulae into groups; the cross represents the mean velocity corresponding to the mean distance of 22 nebulae whose distances could not be estimated individually.” (Direct quotation from caption in Hubble's paper.) Image from Edwin Hubble, “A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae,” Proceedings of the National Academy of Sciences 15, no. 3 (1929): 168–73.

In those days, scientific papers were not as scrupulous about references as they are today. Indeed, some can be called sloppy and unscholarly by modern standards. So, Hubble was not unusual in failing to cite the sources of his data. This has left the impression, found in many popular astronomy books, that all the data were taken with the 100-inch telescope on Mount Wilson by Hubble and Humason. Actually, only four points were from Mount Wilson, recorded by Humason. The bulk of the data in Hubble's paper was from Slipher, taken with smaller telescopes at Lowell Observatory.15 Nevertheless, by 1931 Hubble and Humason had added forty galaxies of their own.

The slope of that line on the velocity v vs. distance r plot, K= v/r, is called Hubble's constant, now designated H. Hubble's law then is v = Hr. Hubble quotes two values based on different analyses of the data: K = 500 kilometers per second per million parsecs for individual nebulae and 530 for nebulae combined into groups.

With these values of K, Humason's NGC 7619 would be twenty million light-years away. As we will see, Hubble's estimate of H was a factor of seven too high, putting Humason's galaxy actually 140 million light-years distant.

Note that, technically, H is the rate of expansion of the universe, which need not, and indeed we now know does not, have the same value throughout the life of the universe. So I will follow convention and define the value H has today, designated H₀, as Hubble's constant; and the more general rate of expansion H we will refer to as the Hubble parameter.

LEMAÎTRE IS NOTICED

In his 1927 paper, two years earlier than Hubble's publication, Lemaître had made an estimate for K (or H) of 625 kilometers per second per million parsecs based on what seems to have been the same data sample used by Hubble.¹⁶ In the paper Lemaître says explicitly, “The receding galaxies are a cosmical effect of the expansion of the universe.”

Lemaître's article began to receive attention 1931 when it was translated into English with the help of Eddington, who, along with Shapley, had been one of Lemaître's mentors and had finally taken notice.17 Lemaître, however, left out of the English translation his calculation of Hubble's constant.¹⁸ In any case, even in the French version Lemaître did not include the crucial plot of velocity versus distance that is really needed to see the effect.

Nevertheless, cosmologists saw the value of Lemaître's work. Eddington noted that Einstein's static universe depended on the cosmological constant having exactly the correct value and any small perturbation would cause the universe to expand or contract. Eddington wrote to de Sitter that Lemaître had provided a “brilliant solution” to the problem, and de Sitter agreed.

Einstein finally came around, and by 1933 so had the astronomical community. Eventually, Einstein abandoned the cosmological constant, calling it his “biggest blunder.” Little did he suspect that it (or something like it) would turn out to be carrying three-quarters of the energy of the universe. Neither de Sitter nor Lemaître discarded the constant from their models, although it would be years before most cosmologists would see any need for the term.

Hubble and Humason continued to measure the redshifts of galaxies, the limit of their spectrograph being reached at forty thousand kilometers per second—fast enough to go to the moon in ten seconds. Hubble did not theorize much and, while he is widely regarded as the discoverer of the expanding universe, he never fully accepted it, keeping his careful, empirical mind open to alternatives, while Shapley became a true believer.¹⁹

Today there is no dispute that Lemaître was the first to associate the redshifts of galaxies with the expansion of the universe. However, Lemaître was not an observer, and theories in science are useless without data to verify them. Hubble's role, with Humason's assistance, was to provide the clinching observations.

In 1935, Hubble gave the Silliman Lectures at Yale University that are reproduced in his classic The Realm of the Nebulae.²⁰ The Silliman Lectures were instituted “to illustrate the presence and providence of God as manifested in the natural and moral world.”

LEMAÎTRE'S PRIMEVAL ATOM

Popular books on astronomy usually use the discovery that the universe is expanding to conclude that the universe therefore had an origin sometime in the finite past. But it doesn't follow. As historian Helge Kragh points out, “When the idea of a finite-age universe was first proposed—and that occurred only two years after Hubble's discovery—most astronomers and physicists resisted it.”21

Eddington was particularly horrified with the idea of an origin to the universe, saying, “philosophically, the notion of a beginning of the present order of nature is repugnant to me.”²² Here's how he imagined it:

I picture…an even distribution of protons and electrons, extremely diffuse and filling all (spherical) space, remaining nearly balanced for an exceedingly long time until its inherent instability prevails…. There is no hurry for anything to happen. But at last small irregular tendencies accumulate, and evolution gets underway…. As the matter drew closer together in the condensations, the various evolutionary processes followed—evolution of stars, evolution of the more complex elements, evolution of planets and life.²³

Lemaître begged to differ. During a conference in London in 1931 on the relation between physics and spirituality, Lemaître proposed that the universe expanded from an initial glob of nuclear matter in an explosion that the British astronomer Fred Hoyle would, in 1948, derisively term the “big bang.” Lemaître announced his idea in a one-page article containing no equations, published in Nature that year.²⁴ He wrote:

If we go back in the course of time, we find all the energy of the universe packed in a few or even in a unique quantum…. If this suggestion be correct, the beginning of the world happened a little before the beginning of space and time. I think that such a beginning of the world is far from repugnant…. We could conceive the beginning of the universe in the form of a unique atom, the atomic weight of which is the total mass of the universe. This highly unstable atom would divide in smaller and smaller atoms by a kind of super-radioactive process.

Note that, unlike some modern theists we will visit later, Lemaître does not argue from general relativistic cosmology because he knew full well that it does not provide a unique scenario for the origin of the universe. Instead, he relies on quantum mechanics, which to this day has not been reconciled with general relativity, although it has with special relativity. Lemaître imagines the universe starts as something like an atomic nucleus containing all the universe's matter, which then spontaneously decays to produce the universe, as we know it.

In 1941, Lemaître published a book in French titled L’hypothèse de l’atome primitif (The Primeval Atom), which was translated into English in 1950.25 Although containing a few equations and a mathematical appendix, it is not a technical manuscript but a wide-ranging discussion of cosmogony and cosmology aimed for the French-speaking public. Lemaître spends a long chapter arguing that his hypothesis in which the universe began as a single, giant nucleus is consistent with all the knowledge of the day.

It is worth noting that Lemaître anticipated a claim that in recent years has become a staple argument among theologians: Not only did the universe itself come into being with the big bang, but so did space and time.

Much has been made of the fact that Lemaître was a Jesuit priest and his notion that the universe began a finite time ago with a giant explosion was informed by his religious beliefs. However, he always insisted that the primeval atom was purely a scientific hypothesis not yet confirmed by the data. Indeed, Lemaître's scenario sounds more like the Chinese creation myth of a “cosmic egg” than what is described in Genesis.

The original typescript of his Nature paper ended with the following sentence that Lemaître crossed out before submitting:

I think that every one who believes in a supreme being supporting every being and every acting, believes also that God is essentially hidden and may be glad to see how present physics provides a veil hiding his creation.26

In other words, the big bang should not be taken as evidence for a creator God since that God is hidden. Many like Lemaître who choose to believe in God despite the fact that his existence is far from obvious have little recourse but to assume that he must have reasons to hide from us. However, this “hiddenness argument” has been shown to fail.²⁷

Lemaître's proposal was largely speculation. He provided no quantitative model. The most that could be said at the time was that Hubble's law, v = Hr, is exactly what you would expect for the particles in an explosion. If they do not collide with one another after the explosion, the faster moving will be farther away at any given time and r should be linearly proportional to v. Certainly the best one can do with the data points in figure 8.3 is fit them to a straight line. That's the way things stood for much of the twentieth century until just two years before the new millennium when the data became far more precise. But we will get to that later.

In the linear model, where H is a constant, then its reciprocal is the age of the universe. Hubble's value of five hundred kilometers per second per million parsecs converts to T = 1/H = two billion years. At the time, this was less than the age of Earth determined from radiative decay, which was estimated to be at least three billion years. You would expect the universe to be older than Earth.

And there were other problems. Judging from their distances as determined from Hubble's law, the galaxies outside our own are all smaller than the Milky Way. In particular, Andromeda was smaller and its stars fainter than expected. It seemed unlikely that we were again so special. For years, these were major defects in Hubble's law.

It was not until 1948 when the 200-inch Hale reflector went in operation at the Palomar Observatory in California that the quantitative problem with Hubble's law was solved. Using Hale, in 1952 Walter Baade showed that there were two distinct kinds of Cepheids.28 Hubble had assumed one kind to measure the distance to Andromeda, while Shapley had used another kind for his measurements of the distances to globular clusters in the Milky Way. So, Andromeda was not smaller and its stars fainter than those in our galaxy. It was just farther away than Hubble thought. His value of H was seven times too large and so his distance estimates were seven times too small.

The current best value of Hubble's constant is about seventy kilometers per second per million parsecs, giving an age for the universe of T = 1/H = fourteen billion years. This estimate is based on the assumption that H is a constant. As we will see later, this is now known not to be true and, as of this writing in 2014, the best estimate of the age of the universe is 13.8 billion years, with a small and statistically insignificant (despite media hype) disagreement on the precise number among observers using different techniques.

“THEREFORE, GOD EXISTS!”

Against his expressed wishes, Lemaître's big bang was and still is being used by theologians and believing scientists to claim scientific evidence for a divine creation. On November 22, 1951, Pope Pius XII spoke before the Pontifical Academy of Sciences where he announced that modern science and the Church are converging on the same fundamental truths.²⁹

Introducing a theme that would be expanded upon by religious apologists in succeeding decades, the pope said: “According to the measure of its progress, and contrary to affirmations advanced in the past, true science discovers God in an ever-increasing degree—as though God were waiting behind every door opened by science.” He identified two essential characteristics of the cosmos “which science has, in a marvelous degree, fathomed, verified and deepened beyond all expectations (1) the mutability of things, including their origin and their end; and (2) the teleological order which stands out in every corner of the cosmos.”

Pius XII gave examples of mutability, that is change, in both the microcosm and macrocosm, such as phase changes and chemical changes in matter, emission of radiation by atoms, and radioactivity of nuclei.

Moving to the cosmos, the pope says: “Everything seems to indicate that the material universe had in finite times a mighty beginning, provided as it was with an indescribably vast abundance of energy reserves, in virtue of which, at first rapidly and then with increasing slowness, it evolved into its present state.”

The pope concludes:

[Modern science] has followed the course and the direction of cosmic developments, and, just as it was able to get a glimpse of the term toward which these developments were inexorably leading, so also it has pointed to their beginning in time some five billion years ago. [Note: This was a reasonable estimate at the time]. Thus, with that concreteness which is characteristic of physical proofs, it has confirmed the contingency of the universe and also the well-founded deduction as to the epoch when the cosmos came forth in the hand of the Creator.

And, in the lines that have been quoted frequently in the decades since:

Hence creation took place in time. Therefore, there is a Creator. Therefore, God exists.

Interestingly, in no place in his speech does the pope refer to specific Catholic doctrines or to the Bible. While he mentions “cosmic developments” that point to the “beginning of time some five billion years ago,” he does not mention that Genesis implies a much more recent creation—on the order of ten thousand years. He also does not mention the doctrine of the immutability of species unmistakably present in Genesis.

Of course, that's the advantage of being pope. It is he who determines the official doctrines of the Catholic Church, not the Bible. Poor Protestants. They do not have available to them the same continuous line of authority going back to Christ and must rely on an obviously flawed book of myths thousands of years old.

Even so, in 1951 there still was no convincing evidence for the big bang, so it wasn't proof of anything. As Kragh points out, “At the time the pope gave his presentation of cosmology, the field was not characterized by harmonious agreement, but on the contrary, by a fierce controversy.” The pope's message was actually quite misleading, leaving the impression among laypersons that “the biblical Genesis had literally been proved by big-bang cosmology.” Lemaître knew this was not the case and managed to get the pope to slightly moderate his views in later speeches.30

TIRED LIGHT

If Hubble wasn't totally sold on the expanding universe, you can bet others weren't as well. They were, after all, just doing their jobs as scientists: question everything until the data supporting a theory are completely convincing. So, cosmologists sought other explanations for the undeniable empirical fact of redshifts in the spectra of galaxies. If the redshifts weren't the Doppler effect of receding velocities, then what were they?

A plausible explanation was proposed by one of the more interesting characters in the history of astronomy, Caltech astronomer Fritz Zwicky. Zwicky was born in 1898 in Varna, Bulgaria, where his father was Swiss ambassador. In 1925 he joined the Caltech faculty and worked most of his life at the Palomar and Mount Wilson Observatories. Zwicky had many ideas that were ahead of his time such as galaxies occur in clusters.

In 1929, Zwicky suggested that the redshift was caused by tired light: photons coming from great distances simply lose energy by interacting with matter, including perhaps other photons, along the way. As the photons lose energy, their corresponding wavelengths will increase toward the red.

Although this idea stuck around in various forms for decades, it was eventually falsified by a surface-brightness test proposed by American theoretical physicist Richard Tolman. In a static universe, the intensity of light from a star or a galaxy will fall off as 1/r², where r is the distance to the galaxy, while the apparent area also drops off in the same way; so the observed brightness per unit area will be constant. In an expanding universe, the brightness falls off more rapidly with distance for two reasons. First, because the object emitting the photons is moving away, each photon has to travel a greater distance than the one before, resulting in a lower rate and decreased intensity. Second, the object appears larger than it really is because the light we observe was emitted when it was closer. The best measurements of surface brightness supported an expanding universe and ruled out the tired-light hypothesis.

VARIABLE CONSTANTS

Another suggestion made for the observed redshifts was that the speed of light is decreasing with time. Eddington pointed out that this contradicted special relativity, which assumes c is constant. As we saw in chapter 6, the assumption that the speed of light in a vacuum is a constant is now built into physics. But, as always, we must rest our case on data rather than on theory. Since special relativity has been consistent with many thousands of experiments conducted for over a century, we can sit comfortably on its foundation until the data tell us to do otherwise.

In 1938, Paul Dirac proposed a model in which Newton's gravitational constant G varies with time.³¹ This contradicted the assumptions of general relativity and led to a universe only seven hundred million years old. When he realized this, Dirac abandoned the idea. Today we recognize that G and c are arbitrary constants whose numerical values just set the units with which we are working.³²

MILNE'S COSMOLOGY

In the 1930s, Edward Arthur Milne, brother of A. A. Milne, creator of Winnie-the-Pooh, proposed a cosmology of his own that did not depend on general relativity.33 He denied that space is curved or expands. In fact, space was not something physical but simply a system of reference.³⁴

In my 2006 book The Comprehensible Cosmos, I described the procedure Milne outlined by which we can make observations solely with a clock.³⁵ I thought Milne presented a precise and objective implementation of the way we actually find out what is out there in the world beyond our individual selves and describe it in terms of a space-time model. All we do as observers is send and receive signals. Following Milne, I showed how with just a clock, a pulsed light source, and a detector we can develop a picture of the world. We simply send out signals and receive replies analogous to radar echoes. Without any meter sticks or other devices to measure distances, just measuring times, we can determine a quantity we call “distance” from which we can formulate a model of the outside world. In this scheme, the speed of light is constant by convention and so special relativity falls right out.

Milne's model universe was made of randomly moving particles like molecules in a gas. He further made the reasonable assumption that the universe should look the same to all observers. This cosmological principle can be traced back to Nicholas de Cusa in the fifteenth century (see chapter 2).³⁶

From this model, Milne was able to derive Hubble's law v = Hr and, thus, the expansion of the universe without general relativity. However, he did not derive much else. He predicted that Newton's gravitational constant G would increase with time, but so slowly as to be undetectable. Actually, he did not regard this time variation to be subject to experimental test since it involved another kind of time he invented, kinematic time, which is not measured with clocks.

Although highly unconventional, Milne's cosmology attracted considerable attention in the 1930s. Hubble, in particular, was favorable of it and mentions it near the end of The Realm of the Nebulae where he spends a few pages on theory.37

However, Milne turned off a lot of people with his mixing of cosmology and a rather (also) unconventional theology. In his 1935 book, he says that ultimate questions of cosmology need reference to God. He frequently mentioned God in his speeches and other writings. Unlike Lemaître, who was careful to leave religion out of his science, Milne believed that theological and metaphysical arguments had a role to play in science, especially in regard to the creation of the universe.³⁸ He wrote: “Investigators who leave out God, the raison d’être of the universe, find themselves lamentably handicapped in dealing with cosmological questions.”³⁹

Even worse than Milne's theology, from the standpoint of the empirical scientific community, was his extreme rationalism. Milne placed logic and reason over observation and experiment. He wrote:

The philosopher may take comfort from the fact that, in spite of the much vaunted sway and dominance of pure observation and experiment in ordinary physics, world-physics propounds questions of an objective, non-metaphysical character which cannot be answered by observation but must be answered, if at all, by pure reason; natural philosophy is something bigger than the totality of conceivable observations.⁴⁰

Milne's theory suffered the fate of most theories that put too much emphasis on reason, logic, and mathematics (and, as in his case, revelation) and not enough on data: it failed to provide a falsifiable empirical test. In science, a theory that is not falsifiable is history (or at least should be), and so Milne's cosmology was ultimately ignored as general relativistic cosmology and the big bang, aided by developments in submicroscopic physics came to the fore. But, as we will now see, that did not happen overnight.

MISSING MASS

The 1930s also provided the first hints of what would become another unexpected and enormously significant feature of the universe. In 1932, Dutch astronomer Jan Oort discovered that the masses of luminous objects such as stars and dust in the galaxy were insufficient to account for the observed orbital motions of stars. The following year, Zwicky noticed the same effect in the orbital speed of galaxies inside galactic clusters. From his measurements and applying Newton's laws, he calculated that the mass of the Coma cluster is four hundred times its luminous mass. He named this invisible gravitating stuff dunckle materie—dark matter.41

In 1939, American astronomer Horace Babcock measured the rotation curve of the Andromeda galaxy, which is a plot of the velocity of stars against their distance to the center of the galaxy. Based on Newton's law of gravity, that velocity should fall off with distance, as it does for planets in the solar system. However, as later measurements in the 1960s and 1970s verified, the rotation curve stays flat well past the main luminous part of the galaxy, indicating that the stars are moving through a roughly uniform distribution of invisible matter.

We now know that dark matter constitutes 26 percent of the mass of the universe, while all the luminous matter we see with optical telescopes comprises only 0.5 percent. Furthermore, as we will see next, the great bulk of dark matter is composed of something besides familiar atomic matter, still not identified.

RADIO ASTRONOMY

The 1930s also saw the opening up of a new window on the universe. In 1933, Bell Telephone Laboratories’ engineer Karl Jansky detected radio waves from beyond Earth.⁴² This would lead to a new field of radio astronomy that explores the universe in a spectral region far from the visible region and plays an important role in cosmology.