STATIC FROM THE SKY

As we saw in the previous chapter, in 1949 Ralph Alpher and Robert Herman predicted that if the early universe was as hot and dense as implied by the big-bang model, then the universe today should be bathed in thermal radiation that has been cooled to about five degrees Kelvin because of the universe's expansion in the billions of years since. Most physicists and astronomers at the time ignored the prediction. They did not take the big bang seriously, perhaps because of its failure to account for the production of chemical elements beyond helium except for, at most, trace amounts of lithium and beryllium.

Or, as with Fred Hoyle and his collaborators, they may have objected to the implication being drawn by religious apologists, including the pope, that the big bang provided scientific evidence for divine creation.

This lack of enthusiasm for the big bang was further fortified by the remarkable success of Hoyle, William Fowler, Margaret Burbidge, and Geoffrey Burbidge in explaining the formation of the heavier elements in the cores of dying stars. These stars collapse gravitationally after they have exhausted all the hydrogen they use for fuel. The combination of high temperature and high density needed for nucleosynthesis exists in these collapsing cores, but not in the early universe.

Nevertheless, the idea of a cosmic background radiation kept cropping up in the minds of researchers apparently unaware of Alpher and Herman's work. In the early 1960s, Princeton physicist Robert Dicke was investigating the possibility that the universe might oscillate in a series of big bangs and big crunches, which is one of the allowed solutions of Friedmann's cosmological equations. He reasoned that, during the current phase of oscillation, our universe was once much hotter than it is now. In that case, it might generate thermal radiation that has been cooled off since by the universe's expansion.

In 1964, Dicke's former student, James Peebles, estimated that the temperature of this relic radiation should be on the order of ten degrees Kelvin, in the microwave region.

Also at Princeton at the time were Peter Roll and David Wilkinson, who had built a radiometer capable of measuring microwaves of three centimeters’ wavelength. So a collaboration was formed to seek evidence for a cosmic microwave background.

However, in an oft-told tale, notably in the bestseller The First Three Minutes by Nobel laureate physicist Steven Weinberg,1 the Princeton physicists were beaten to the punch serendipitously by two researchers working at the Bell Laboratories forty miles away in Holmdel Township, New Jersey. In 1963, radio astronomers Arno Penzias and Robert Wilson had started to work with a highly sensitive, 7.35-centimeter microwave transmitter-receiver with a horn antenna and state-of-the-art cryogenic technology, including a maser amplifier. The instrument was originally designed for communication with the Bell System satellite Telstar. Bell's European partners in the project had developed a similar system, and the Bell instrument was a backup. As it turned out, the backup wasn't needed so Penzias and Wilson could use it for radio astronomy.

The radio astronomers decided to try to measure the radiation intensity from our galaxy outside the galactic plane, that is, away from the Milky Way. In the spring of 1964, they detected an excess of static that could not be blamed on their antenna and electronic circuits. They did everything they could to find an instrumental source of the noise, including cleaning up “white dielectric material” left by pigeons on the antenna, and concluded the static was from an external source. Since the signal was coming in uniformly from all directions, this ruled out Earth's atmosphere or the Milky Way as sources.

Radio engineers express noise at a given wavelength in terms of the temperature of a blackbody that would give the same amount of noise. The Penzias and Wilson results were equivalent to 3.5 degrees Kelvin (3.5 K) antenna temperature.

By means of the grapevine, the two New Jersey groups found out about each other and began to communicate. In 1965, Penzias and Wilson presented their observations in a paper in Astrophysical Journal with the unassuming title, “A Measurement of Excess Antenna Temperature at 4080 Mc/s.”2 As to the interpretation of the data, the authors referred to the preceding article in the same issue by Dicke, Peebles, Roll, and Wilkinson titled “Cosmic Black-Body Radiation.”³ Penzias and Wilson would receive the 1978 Nobel Prize for Physics.

It did not take the scientific community long to recognize the significance of what would eventually amount to the most important cosmological discovery since the redshift of galaxies. However, more measurements were needed to confirm that what was being detected was in fact thermal radiation. Only one wavelength had been observed. In early 1966, Roll and Wilkinson reported observations at 3.2 centimeters, confirming that microwave radiation is in fact out there. But more was needed.

THE SPECTRUM

The Planck spectrum for blackbody radiation at 3 K is shown in figure 10.1. Note that the shape is different from figure 6.1 since that plot was made against frequency whereas here the plot is against wavelength. Also, here both axes are logarithmic.

Several points are to be noted: The measurements by the two New Jersey teams fall in what is called the Rayleigh-Jeans portion of the spectrum, which is given by classical wave theory described in chapter 5. To be certain they were seeing blackbody radiation, it was necessary to map the full spectrum. However, while the atmosphere is relatively transparent to microwaves, it becomes increasingly opaque as we move down into the infrared region of the spectrum—just where at 3 K the deviation from classical wave theory takes place and the spectrum falls off because of quantum effects.

As far back as 1941, two optical astronomers, Walter Adams and Andrew McKellar, observed a splitting into three lines of an interstellar absorption line identified with the molecule cyanogen (CN). McKellar estimated that two of the split lines were the result of some unknown perturbation that corresponded to a temperature of 2.3 K. After the discovery of the microwave background, it was realized that this splitting was caused by blackbody photons with a wavelength of 0.263 centimeters, right at the peak of the Planck spectrum in figure 10.1.⁴

The big bang was back in business. The remnant of the explosion that produced the universe presumably had been detected. Of course, there were still a few doubters. Fred Hoyle and his loyal band of steady-staters did their honest best to play devil's advocate in seeking other explanations for the observed radiation. But these were all ad hoc and lacked empirical support. Gradually, the steady-state model lost its remaining credibility, although Hoyle and Geoffrey Burbidge remained unconvinced that the big bang had been confirmed. They demanded even more evidence.

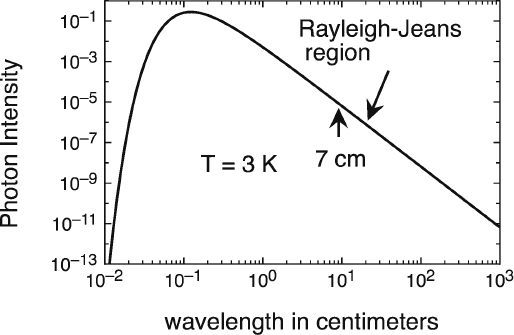
Figure 10.1. The predicted Planck blackbody spectrum at 3K. The vertical scale is given in photons per cubic centimeter volume per centimeter wavelength interval. The linear portion is the classical Rayleigh-Jeans spectrum that falls off as the fourth power of wavelength. The Penzias-Wilson measurement at 7.35 centimeters is indicated. The Roll and Wilkinson measurement at 3.2 centimeters is just below that. Neither covered the quantum region. Image by the author.

BIG-BANG NUCLEOSYNTHESIS REBORN

Back in 1953, Alpher, Herman, and James Follin had published a lengthy paper detailing what the best physics knowledge at the time had to say about the conditions of the early universe.5 Weinberg called it “the first thoroughly modern analysis of the early history of the universe.”⁶ However, the authors did not consider nucleosynthesis nor mention microwave radiation.

With the discovery of the cosmic microwave background (CMB) in 1965, the big bang moved to the front burner and new, independent calculations of big-bang nucleosynthesis were performed by Yakov Zel’dovich in Russia, Hoyle and Roger Taylor in England, and Peebles in the United States. (Another little insight into how science works: Even though Hoyle bitterly opposed the big bang, he was not beyond making serious, unbiased calculations assuming the model).

While by then it was clear that the elements above helium are largely produced in stars, these represent only about 1 percent of the total mass of atoms in the universe. The rest is about 75 percent hydrogen and 25 percent helium, and Hoyle admitted that the conditions in stars were not such as to produce a 25 percent abundance of helium. Still, he was not ready to accept the big bang and continued to look for other explanations. But a new generation of cosmologists would prove beyond a reasonable doubt that the big bang happened.

DAVID SCHRAMM: THE GENTLE GIANT OF COSMOLOGY

In The First Three Minutes, Weinberg makes a diversion, spending a chapter trying to understand why the discovery of the CMB took so long and happened by accident, when the knowledge and technology were there earlier.7 One reason he mentions is the lack of communication between theorists working on the big-bang model and radio astronomers. We saw a similar situation earlier with Edwin Hubble and other astronomical observers having little knowledge of relativistic cosmology, while relativistic cosmologists such as Alexander Friedmann paid no attention to observations. Georges Lemaître was an exception. Although he made no observations himself, at least he related his theories to the data.

In the exciting physics era in which I participated that flourished in the 1960s and 1970s, I saw quite the opposite. By then, interdiscipline communications had greatly improved. Although we still did not have the Internet, we had phones, faxes, photocopiers, and jet liners that enabled us to meet and talk to one another. Theorists and experimenters went to each other's seminars, ate lunch together, and shared the same coffee pot in the lab. In the two sabbaticals I spent at the Nuclear Physics Laboratory at Oxford University, everybody stopped work once in the morning for coffee and once in the afternoon for tea (best and cheapest tea in town), sitting together at low tables in a big common room, talking the latest physics. Often a distinguished visitor would join us.

By 1979, the lines between areas of expertise in physics and astronomy had also begun to crumble. One of the primary creators of a new way of doing science was a larger-than-life, six-foot-four, 240-pound, redheaded mountain-climbing, Olympic-trials Greco-Roman wrestling finalist named David Norman Schramm, to whom this book is dedicated. Schramm received his doctorate in 1971 from Caltech under Willy Fowler, the future Nobel Prize winner who, as we have seen, was one of Fred Hoyle's collaborators on stellar nucleosynthesis.

Joining the faculty of the University of Chicago in 1974, Schramm was chair of the Department of Astronomy and Astrophysics from 1978 to 1984 and became Vice President for Research in 1995. In Chicago, Schramm was the mentor and leader of a team composed of new brand of theoretical physicist, one who has mastered nuclear physics, elementary particle physics, astrophysics, and relativistic cosmology. Members of this team would put this combined knowledge to work in providing a remarkably detailed picture of the early universe and see it successfully tested against the increasingly precise astronomical data that was coming in, especially from space telescopes. A new field was born called particle astrophysics, and David Schramm was its father.

With the help of the Leon Lederman, another future Nobel Prize winner and director of Fermi National Laboratory (Fermilab) near Chicago, in 1982 Schramm organized a particle-astrophysics center at the lab that would, working with the University of Chicago, pioneer much of this remarkable work. I got to know Schramm and his team when I became involved in very high-energy gamma-ray and neutrino astrophysics after working on neutrino experiments at the Fermilab accelerator. He was always kind, patient, and good-humored, and both his public and technical lectures were joys to experience. I considered him a friend; but then he had hundreds.

Schramm had bought a house in Aspen, Colorado, in 1980 and became involved with the Aspen Center for Physics, which had regular summer workshops that I attended on occasion. He usually flew his own plane, incorporated as Big Bang Airlines, between there and Chicago. (He was a licensed commercial pilot.) On December 19, 1997, he was on his way to Aspen for the holidays when his plane stalled and crashed just after refueling in Denver. Dave was just fifty-two years old. Lederman said he was in heaven having a “terrific argument with God about what happened before the big bang.”

I borrowed the title of this section from an essay in the New York Times by Dennis Overbye.8 A loving but still highly informative biographical memoir was written by one of Dave's outstanding postdocs, Michael Turner. Now possessor of an endowed chair at the University of Chicago, Turner became a major leader in particle astrophysics and was the 2013 president of the American Physical Society.⁹ Turner worked closely with Edward (“Rocky”) Kolb at Fermilab and Chicago, and in 1990 they coauthored the classic monograph on particle astrophysics called The Early Universe.¹⁰

Schramm and collaborators demonstrated that rare processes seen only in elementary particle physics play a crucial role in both the current and early universe. For example, in 1975 they showed that the just-discovered weak neutral current interaction is involved in the collapse of massive stars that produce supernova explosions.¹¹

Schramm always had an interest in neutrinos, which was also my main field of study in those days, so I followed his work closely. The observation by two underground experiments in 1987 of neutrinos from a supernova (SN1987A) in the Large Magellanic Cloud confirmed the important role that these elusive particles play in supernovae.

In a significant paper published in 1977, Schramm, Gary Steigman, and James Gunn showed that cosmology places a limit on the number of types of leptons.12 Lepton is the generic name given to the negatively charged electron, e, and its two heavier companions, the muon, μ, the tauon, τ, and their associated neutrinos, ν_e, ν_μ, and ν_τ. Each lepton is accompanied by an antiparticle. At this time, these three “generations” of leptons, along with related generations of quarks, were established and physicists had no reason to think there might not be more.

The 1977 paper by Schramm and collaborators showed that additional neutrinos would speed up the production of He⁴ and placed the limit at five neutrino types based on then-measured helium abundance. By 1989, the abundance measurements had improved sufficiently to place the limit at three generations. This agreed with measurements of missing energy in colliding-beam accelerator experiments. More neutrinos means more missing energy, that is, energy not accounted for in the detected particles. The amount missing was consistent with three generations and no more.

And so the standard model of elementary particles and forces, which will be discussed in the next chapter, settled on a scheme in which both quarks and leptons are found in just three generations. This was just as Schramm had anticipated. Who would ever have dreamed, except such a dreamer, that cosmology would tell us fundamental facts about the nature of matter on the smallest scale? And that process is continuing to the present day and is likely to carry on for years.

TEMPERATURE IN THE EXPANDING UNIVERSE

Before we delve into the details of big-bang nuclear physics, it will help to get an idea of the energies involved at various stages in the universe's history as they apply not just to nuclear physics but also to the physics at each stage.

Although the universe is expanding very rapidly, the particles present at early times were interacting with one another even more rapidly so that they still thermalized sufficiently to be in a state of quasi equilibrium. This means that the particles can be described as having an absolute temperature T that nevertheless decreases with time as the universe expands.

Most authors writing on this subject will give you the values of the temperatures at various stages in degrees Kelvin, presumably because they figure that these units are more familiar to the reader. But the actual temperature numbers in the early universe are so high as to not be very meaningful by our experience.

More informative is the average kinetic energies of the particles in the universe at any given time, which to an accuracy sufficient for our purposes is given by K = k_BT where k_B is Boltzmann's constant. That is, the temperature of a body is simply the average kinetic energy of the particles in the body. Since k_B is an arbitrary constant that just converts degrees Kevin to energy units, we can set k_B = 1 and measure temperature in energy units.

When we are dealing with atomic, nuclear, and subnuclear processes, the most useful unit of energy and temperature is the electron-volt (eV), which is the kinetic energy an electron gains when it falls through an electric potential of one volt. Atomic processes are characterized by energies of a few eV or keV, where 1 keV = 1,000 eV. Nuclear processes are characterized by energies in the MeV region, where 1 MeV = 1 million eV. Subnuclear processes occur in the GeV and TeV regions, where 1 GeV = 1 billion eV (10⁹) and 1 TeV = 1 trillion eV (10¹²).

Note that colliding-beam accelerators enable us to study the physics of the very early universe. For example, when the Large Hadron Collider (LHC) is upgraded to a total energy of 14 TeV in 2015, it will enable physicists to measure the properties of matter 10^–15 second after the big bang when the temperature was that high.

Figure 10.2 plots the average kinetic energy or temperature of the universe from 10^–43 second, the Planck time, until the present. We will have much to say later about the Planck time and what might have gone on before it. For now, let's begin things at that point.

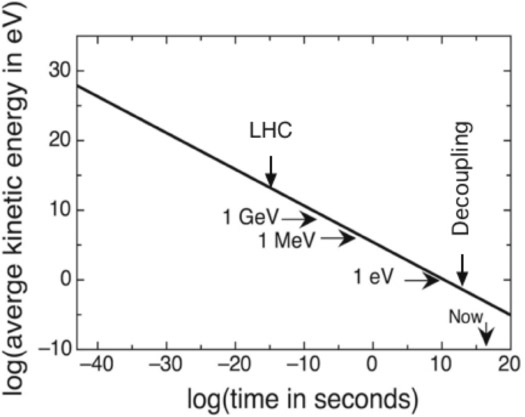
Figure 10.2. Average kinetic energy of the particles of the universe as a function of time after the big bang, on a log-log plot. This can also be considered a plot of the absolute temperature against time, with the temperature in electron volts (eV). Image by the author.

Until 380,000 years after the big bang, all the particles in the universe were in quasi equilibrium at the same decreasing temperature as the universe expanded and cooled. At that time, called decoupling, atomic matter fell out of equilibrium while photons and neutrinos remained in quasi equilibrium. Don't let the log scale fool you. The time between decoupling and now is still 13.8 billion years for all practical purposes.

As the universe expands and cools, various particles drop out of equilibrium. Let me illustrate this with the example of antiprotons. They collide with protons and the two disintegrate into photons and other lighter particles. Consider annihilation into photons. The reaction is

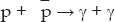
where 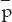is an antiproton and γ is a photon. The photons will carry off the rest energy of the proton and antiproton, plus whatever their initial kinetic energies may be. The reverse reaction can also occur and regenerate antiprotons

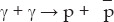
However, since the photons have zero rest energy, their total kinetic energy must at least equal the total rest energy of the proton and antiproton, which is 1876 MeV. So, as long as the temperature of the universe is more than this, antiprotons and protons will remain in equilibrium with about the same number of each. However, once the temperature of the universe drops below 1876 MeV, which happens when it is about 10^–7 second old, photons no longer have sufficient energy to produce proton-antiproton pairs and the two will gradually decrease in number from the mix.

Now, as we will see in chapter 11, a slight asymmetry exists between matter and antimatter so when the antiprotons have all annihilated, some protons are left over. These amount to one in a billion of the photons, electrons, positrons, and neutrinos that remain. If it were not for this asymmetry, all the protons would have annihilated, leaving nothing to make the atoms of stars, planets, and you and me.

Just as antiprotons disappeared from the early universe when the temperature dropped below the value needed to regenerate them, so did the positrons after the universe had cooled further. Let's consider the analogous process, electron pair annihilation into photons:

e⁺ + e^– → γ + γ

In order to regenerate positrons, the reverse reaction must occur:

γ + γ → e⁺ + e^–

Here the photons must have a total energy at least equal to the total rest energy of the positron and electron, which is 1.022 MeV. When the temperature of the universe dropped below this value, which happens when it is about 0.15 second old, photons no longer had sufficient energy to produce the pair and the positrons annihilated. As was the case for protons, one in a billion electrons were left over because of particle-antiparticle asymmetry. Eventually, but not for another 380,000 years, those electrons combined with the protons to form hydrogen atoms. Before that happened, however, the light nuclei formed.

THE LIGHT NUCLEI

He⁴ was not the only light nucleus formed in the big bang. In fact, substantial amounts of H² (the deuteron), H³ (the triton), and He³ were produced, as well as smaller amounts of Li⁷, Be⁷, and Li⁶. In the 1970s, Schramm and his growing stable of nuclear and particle astrophysicists, joined by others worldwide, began an intense program of calculating the primordial abundances of the light elements and comparing them with the data. They obtained remarkable agreement. This program continues to the present day and has been especially advanced by the accompanying great strides in observations.13

To form nuclei we need neutrons. The neutron is 0.782 MeV more massive than the proton and is produced by the following weak interactions:

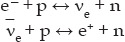
where ν_e and 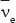are the electron neutrino and electron antineutrino respectively. We will discuss weak interactions and neutrinos, and other fundamental particles in the next chapter. Note that I have used double arrows to indicate that these reactions are reversible.

Because the total mass (rest energy) on the right side of the reactions is greater than that on the left by 0.271 MeV and 1.293 MeV respectively, neutron production for each reaction ceased when the average kinetic energy of the universe dropped below these values. The second reaction, with the higher energy difference, dropped out first at about 0.1 second, while the first reaction continued to produce neutrons until about 2 seconds. After that, the number of neutrons began to diminish to about one-sixth the number of protons as they converted to protons by way of beta decay:

n → p + e^–+ ν_e

The mean lifetime of the neutron is about 880 seconds, with the exact value still in dispute. Big-bang nucleosynthesis is very sensitive to this number.

With the temperature now below 1 MeV, nuclei were able to form without being immediately split apart by the many high-energy photons swarming about. By then, all the positrons had annihilated, as described above, and the neutrinos (and antineutrinos) no longer had anything to do and so turned into a relic thermal cloud—like that of photon background that would form much later. Today this cloud forms the cosmic neutrino background (CνB) with a temperature of 1.95 K, and with little hope of being directly detected in the foreseeable future.

Now let's see how the lighter nuclei form. A proton and neutron can collide to produce a deuteron and photon:

p + n → H² + γ

At first, the lightly bound deuterons were split by the reverse of the above reaction. But when things cooled sufficiently, two deuterons could stick around long enough to produce a neutron and He³,

H² + H² → He³ + n

or a triton and a proton,

H² + H² → H³ + p

He⁴ was then produced by

H² + H³ → He⁴ + n

or by

H² + He³ → He⁴ + p

while Li⁷ was produced by

H³ + He⁴ → Li⁷ + γ

and Be⁷ was produced by

He³ + He⁴ → Be⁷ + γ

And so on. This is not a complete list of reactions, but it should give the idea.

Note in all these reactions, both the atomic number (given by the elemental symbol) and nucleon number are conserved. The first is just charge conservation. The second is a special case of the more general conservation of baryon number that we will discuss later.

The time evolution of the mass fraction of the various light elements relative to protons is shown in figure 10.3. This figure is from Edward Wright's online cosmological tutorial¹⁴ and is based on the paper by Burles, Nollett, and Turner.¹⁵ As we see, the peak in production is at about two hundred seconds and most abundances have leveled off by about one thousand seconds. Li⁶ makes just a brief appearance and neutrons fade rapidly as they are used to form nuclei or decay. Only He⁴ is produced in any substantial quantity.

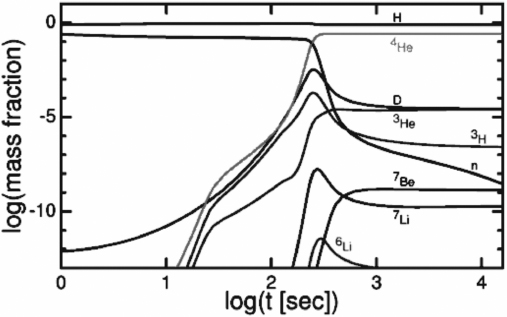
Figure 10.3. The mass fraction of nucleons and nuclei relative to protons in the early universe as function of time. Image courtesy of Edward L. Wright.

Further nucleus building was cut off by the absence of stable nuclei with five or eight nucleons. As we have seen, the heavier nuclei would later be formed in the higher density and temperature of collapsing stars.

The conventional model of big-bang nucleosynthesis used by most nuclear cosmologists depends on only a single parameter, η, the ratio of baryons to photons, which is on the order of 10^–9. Baryon is a generic term in particle physics for a certain class of particles that includes protons and neutrons (see chapter 11). At this stage of the early universe, these and the nuclei made from them are the only baryons that were present.

The He⁴ abundance, about 25 percent of protons by mass, depends only weakly on the conditions of the early universe. This is why even the earliest estimates, made when these conditions were poorly known, were in the right ballpark. On the other hand, the remaining light nuclei, especially deuterons (H²) depend very sensitively on the baryon mass density, ρ_B, which at this time was simply the nucleon density.

The baryon density is usually expressed as the ratio Ω_B = ρ_B/ρ_c, where ρ_c is the critical density, the average density of the universe when it is exactly balanced between positive kinetic energy and negative gravitational energy. The current best value is ρ_c = 9.467 × 10^–30 grams per cubic centimeter. In the Friedmann model described in chapter 8, this is the situation where the curvature parameter k = 0 and the universe is Euclidean, although, as we will see, k = ±1 are not ruled out.

In figure 10.4, the theoretical and measured abundances of the elements are given by their numbers as a fraction of the number of protons. The bands represent the measured quantities with the widths of the bands indicating measurement uncertainties.¹⁶ Rather than look at old theories and data, this graph shows the latest as of this writing, where data from the Wilkinson Microwave Anisotropy Probe (WMAP) satellite have enabled a significant improvement over previous results.¹⁷ While even more precise results from the Planck satellite are now coming in, the WMAP data suffices for our purposes.

The abundances are plotted as a function of Ω_Bh², where h is a dimensionless factor that allows for possible changes in the empirical value of the Hubble constant H₀ (h here is not to be confused with Planck's constant ). That is, cosmologists write H₀ = 100h kilometers per second per megaparsec. The current estimate is h = 0.71.

Estimating the primordial abundances of elements is no easy task. One has to rely on measurements made in the current universe and then figure out how much is primordial.

He⁴ is also produced in stars in the basic fusion processes going on at their cores, but the stars don't disperse any unless they explode into supernovae, and this only happens for the heaviest stars. He⁴ is observed in hot, ionized gas in other galaxies and in so-called metal-poor stars, where astronomers use the term “metal” to refer generically to any element above helium, so this is likely mostly primordial. Some disagreement still exists on the exact fraction of He⁴ relative to protons and calculations are continuing to improve.18 Indeed, as with the constraint placed by cosmology on the number of neutrino species mentioned earlier, the helium abundance is sensitive to the exact lifetime of the neutron so, once again we see the important role subatomic physics plays in cosmology and vice versa.¹⁹

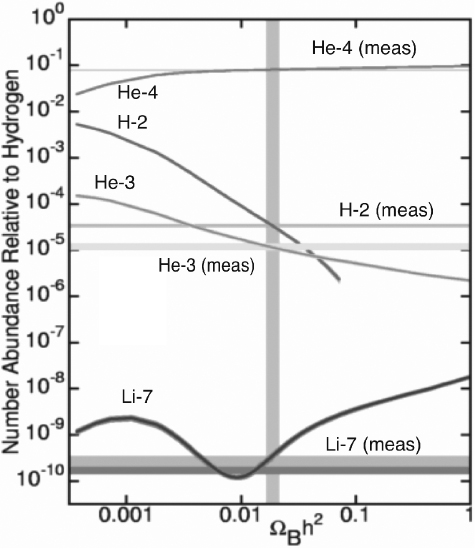
Figure 10.4. Number abundance relative to protons of various nuclei as a function of the baryon density. The bands show the latest measured quantities. The widths of the bands indicate the measurement errors. Image courtesy of Edward L. Wright.

Deuterium, H², is a very loosely bound nucleus composed of a proton and a neutron; it is easily destroyed by many astrophysical processes. The best recent estimate of its primordial abundance comes from observing the absorption lines in very distant intergalactic clouds where the sources are quasars.

Li⁷ is both produced and destroyed in stars. Its primordial abundance has been estimated from its abundance in the atmospheres of the oldest stars in the halo of our galaxy, which are believed to not have depleted much of their lithium.

Stars burn primeval H² into He³ but measurements indicate that the sum of the two is relatively constant so the He³ abundance is estimated by subtracting out the H² abundance estimated elsewhere.

As we can see from figure 10.4, the agreement of the big-bang nucleosynthesis model with the data is truly remarkable. The primordial abundances of four nuclei are precisely calculated from a single parameter, the baryon density. All except He⁴ are highly sensitive to that parameter, although the correct abundance is calculated. All five quantities are in complete agreement with the data.

Thanks to David Schramm and his students and collaborators, the big-bang model is strongly validated by these results. None of the alternatives that are still being tossed around at this time even come close to matching this result. Indeed, they have no idea how to do it. Let's face it. The big bang happened.

ON TO ATOMS

Thirty minutes after the universe first appeared, things quieted down. At that time the temperature was three hundred million degrees and the average kinetic energy about 25 keV and falling. Nuclear processes stopped because the temperature was now too low. Electrons, which were once as common as photons, almost completely annihilated with positrons except for one in a billion left over as a result of a slight asymmetry between matter and antimatter. This asymmetry, without which we would not have the universe as we know it is yet to be completely understood. It will be discussed further in chapter 11.

At this point, most of the universe (excluding dark matter) was now photons (69 percent) and neutrinos (31 percent), with a billion times fewer protons, electrons, and He⁴ nuclei, and even much smaller numbers of deuterons, He³, Li⁷, and Be⁷. Neutrons have disappeared, either by beta decay or by being absorbed into nuclei.

It is no coincidence that the number of protons (plus other nuclei) and electrons match, although some religious apologists have claimed this is yet another fine-tuning coincidence arranged by God.²⁰ In fact, the equality follows from conservation of electric charge, on the reasonable assumption, verified by observations, that the total charge of the universe is zero.²¹

The period of the universe we have described so far is called the era of radiation dominance because photons continue to outnumber everything else, except neutrinos. Unlike neutrinos, these photons were still interacting importantly with the rest of matter.

A note of clarification: Cosmologists make a distinction between what they call “radiation” and what they call “matter.” A particle is called radiation when its kinetic energy is much greater than its rest energy, so that it travels at or very near the speed of light. In that case, its motion must be described by the kinematics of Einstein's theory of special relativity. Since the highest mass particles in the early universe are nuclei with rest energies less than a few GeV, everything was radiation until about 10^–10 second, according to figure 10.2.

Since it has zero rest energy, a photon is always radiation. A neutrino is radiation until its kinetic energy drops below its rest energy, which is no more than on the order of 0.1 eV, five million times smaller than the electron's mass (see chapter 13).

When a particle's rest energy is much greater than its kinetic energy, it is called matter, although even photons and other stuff termed radiation are fully material so the distinction is quite misleading. These particles haves speeds much less than c.

Once the temperature of the universe has dropped below about 100 MeV, which happens when the universe is about 10^–5 second old, the kinetic energies of particles such as protons and nuclei become much lower than their rest energies and can be adequately described by nonrelativistic Newtonian kinematics.

For thousands of years, radiation in the form of photons would continue to dominate the universe. As mentioned, this era is referred to as radiation dominance. However, the energy density of radiation (all kinetic energy) falls off as 1/a⁴, where a is the scale factor of the universe, while the energy density of matter (all rest energy) falls off as only 1/a³. So, by about seventy thousand years after the big bang, the energy density of matter caught up to and exceeded the energy density of radiation and the universe entered the era of matter dominance.

Up until this time, the universe was opaque because photons had all these electrically charged electrons and nuclei with which to interact. An observer inside the universe (obviously not human) would not be able to see by means of light at any wavelength since photons did not go very far, as in a thick fog. Then, when the temperature had cooled to a few thousand degrees and the kinetic energy dropped to a few tenths of an electron volt, electrons and nuclei started sticking together into atoms.

This process is called recombination, which is silly because nuclei and electrons were never combined into atoms in the first place. But, that's what it is called in chemistry, where atoms usually come first. In any case, the oppositely charged particles all combined into neutral atoms (remember there were equal numbers) and the photons no longer had anything but themselves with which to interact. This important moment in history, which occurred 380,000 years after the big bang, we have seen is called decoupling. The universe became transparent and the photons formed a thermalized cloud that, in another 13.8 billion years would cool to 3 K and form the cosmic microwave background.