WRINKLES IN TIME

As the decade of the nineties began, skeptics who had their own favorite theories were still questioning both the big bang and inflation.1 In January 1990, at a meeting of the American Astronomical Society held in Arlington, Virginia, the first results from COBE were presented by John Mather, the principle investigator of FIRAS, the Far Infra-Red Absolute Spectrophotometer, one of the three onboard instruments. As described by George Smoot and Keay Davidson in Wrinkles in Time, when Mather showed the graph in figure 13.1, “A moment's silence hung in the air as the projection illuminated the screen. Then the audience rose and burst into loud applause.”² The blackbody nature of the CMB had been conclusively confirmed.³

At this point it seemed that the big bang could no longer be held in doubt. No other proposed alternative could explain this result without ad hoc assumptions. However, inflation was still not out of the woods.

Bitter opponents such as the prominent astronomers Fred Hoyle and Geoffrey Burbidge, whose great contributions to stellar nucleosynthesis are not to be diminished, continued to speak out and even claim that inflation was already falsified by the lack of empirical confirmation.

But they were a bit premature.

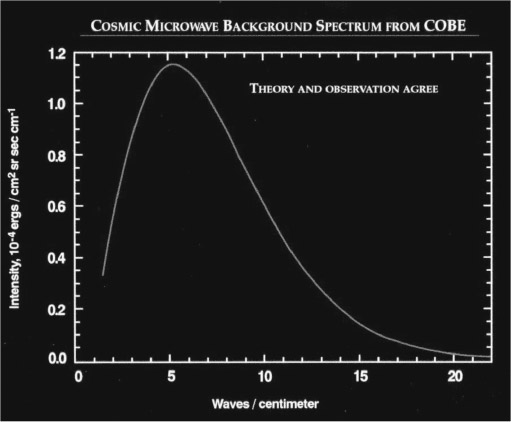
Figure 13.1. The CMB spectrum measured by FIRAS. The bottom scale is the reciprocal wavelength, which is proportional to frequency. The curve is a fit to the Planck blackbody spectrum for a temperature of 2.75 K. Image courtesy of NASA/GSFC.

On April 23, 1992, Smoot showed a series of maps of the CMB sky before a packed audience at an American Physical Society meeting in Washington, DC. To another standing ovation like the one given to his colleague John Mather two years earlier, Smoot demonstrated what he called “wrinkles in time” that fully confirmed the predictions of inflation.

Stephen Hawking, with some hyperbole, called it “The scientific discovery of the century, if not all time.” Smoot said it was “like seeing God.”4 The National Enquirer (or a similar publication) showed its version of the data—the face of Jesus in the sky.

The temperature variations of the CMB predicted by inflationary cosmology were, after a decade of intense effort, finally confirmed.5 Mather and Smoot would share the Nobel Prize for Physics in 2006.

In The Inflationary Universe, Alan Guth presents a graph of the COBE results redrawn in less-technical fashion, which is reproduced with his permission in figure 13.2.⁶ The graph presents the CMB temperature difference squared averaged over all directions in the sky as a function of the separation angle of the two directions measured by the differential radiometer, from 0 to 180 degrees. The data agree perfectly with the shape predicted by inflation, although in the book Guth does not make any claim about the magnitude of the effect, which was adjusted in the figure to fit the data.

However, it was soon realized that if the anisotropy had not come in at about a magnitude of one part in one hundred thousand, inflation would have been in big trouble indeed, if not falsified.

In science, a model that is not falsifiable is not science. But when a model passes a very risky, falsifiable test such as this was, it earns the right to be taken seriously. Still, a note of caution must be added based on the history of science. Even when a model passes a test that could have falsified it, this does not mean that the model has been proved conclusively and will not someday be superseded by a better model. As we will see, however, when included as a part of a full-blown cosmological model, inflation still has more to offer than any alternative can match.

In a paper interpreting their results, the COBE team compared its observations with many proposed models and basically found that its measured anisotropies were very large compared to the inhomogeneities observed in galaxy surveys and so must be primordial. They concluded that COBE has provided “the earliest observational information about the origin of the universe, going back to 10^–35 second after the big bang.”⁷

At first it was thought that primordial fluctuations at the time of inflation on the order of 10^–5 were insufficient to produce the galaxies given the observed density of matter. However, the answer was quickly found (someone in Smoot's audience had actually shouted it out): “Dark matter!”

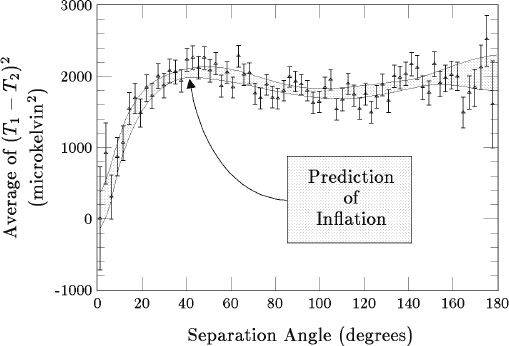
Figure 13.2. CMB temperature difference squared averaged across the sky as a function of the separation angle of the COBE differential microwave radiometer compared with the prediction of inflation. The magnitude was adjusted to fit the data. Image courtesy of Alan H. Guth.

How much was needed? As we will see, exactly the amount that seemed to be present—about five times as much mass as is carried by visible matter.8

As shown in figure 13.2, for separation angles above about thirty degrees the distribution is basically flat, which confirms the prediction of scale invariance. We need not get into the more-detailed shape since succeeding experiments, yet to be discussed, would provide greatly improved data and smaller angles would reveal remarkable structure that defined the early universe in great detail.

NEW WINDOWS ON THE UNIVERSE

CMB observations were not the only significant achievements of the 1990s, in what was another banner decade for astronomy and cosmology. I will only briefly mention a few selected examples that bear most directly on cosmology.

In 1990, the Hubble Space Telescope (HST) was carried into orbit by the space shuttle Discovery. Unfortunately, the primary mirror was severely flawed and had to be repaired in orbit. This was accomplished by shuttle astronauts in 1994, a spectacular achievement that in my mind was the most important contribution to science made by the whole shuttle program. Other Hubble-servicing missions were carried out in 1997, 1999, 2002, and 2009.

Covering the near-ultraviolet, visible, and near-infrared regions of the spectrum, Hubble provided the most detailed images ever recorded in astronomical history and mapped the universe out to the horizon. Still operating at this writing after twenty-three years, HST contributed to cosmology by providing greatly improved estimates of the Hubble constant and other key parameters. In its deep field observations, HST would show that the farthest, oldest galaxies were smaller and more chaotic than the closer, younger spirals, putting yet another nail in the coffin of the already-so-dead steady-state model.

The year 1990 also saw the Keck I multi-mirror ten-meter optical telescope installed on Mauna Kea. It was joined by Keck II in 1998. Recall that Mauna Kea is the best observational site on Earth and capable of peering into the infrared as well as visible part of the spectrum. One of the most productive ground-based astronomy projects of recent years, the Keck telescopes were among the first to find evidence for planets around stars (besides the sun). By determining the orbital speeds of stars near the center of our galaxy, the Keck telescopes helped establish that a four-million solar mass black hole resides at the center of the Milky Way.

In 1993, the Very Long Baseline Array (VLBA) of ten radio telescopes was distributed from Hawaii to the Virgin Islands and operated remotely from New Mexico. By utilizing long-baseline interferometry, the array was able to achieve angular resolutions from 0.17 milliarcseconds to 22 milliarcseconds over a band of ten wavelengths from 0.7 centimeters to 90 centimeters. The array discovered two giant black holes, each 150 million times more massive than the sun and separated by only twenty-four light-years! They are located at the center of the galaxy 0402+379 that is 750 million light-years from Earth.

Indeed, it is now clear that most, if not all, large galaxies have supermassive black holes at their centers.

In 1995, the Infrared Space Observatory (ISO) was placed in orbit. It was designed to study the region of the spectrum from 1.5 to 196.8 microns. ISO made twenty-six thousand successful observations before failing in 1998.

Moving to the gamma-ray region of the spectrum, back in 1967, the Vela satellites whose purpose was to detect nuclear-weapons tests on Earth had serendipitously detected nonrepeating bursts of gamma rays located randomly in the sky. It was generally assumed that they were from inside our galaxy because of their brightness.

In 1991, the Compton Gamma Ray Observatory was launched into space. One of the instruments onboard, BATSE (Burst and Transient Source Experiment) was designed to detect and analyze gamma-ray bursts. It found an average of one a day, for a total of 2,700 detections. From these observations, the gamma-ray bursts were determined to originate from distant galaxies and thus to be emitting enormous amounts of energy.

Recently, NASA announced that the Hubble Space Telescope has detected such a burst and calculations have identified it as the collision of two neutron stars.9

VERY HIGH-ENERGY ASTROPHYSICS

Although the signals measured by radio telescopes are usually described as radio waves, they are composed of photon particles just like any other electromagnetic wave. The energy E of a photon in the beam of photons that make up an electromagnetic wave is given by E = hc/λ, where λ is the wavelength. You can write this E = 1.97 × 10^–7/λ eV when λ is in meters. Since the longest wavelength for the VLBA is about one meter, the photon energy in that case is less than a millionth of an electron-volt.

At the other end of the spectrum, the EGRET (Energetic Gamma Ray Experiment Telescope) detector on the Compton spacecraft had a maximum detectable photon energy of 30 GeV = 3 × 10¹⁰ eV, corresponding to a wavelength on the order of 10^–17 meter.

At this time, there were a few, including myself, who sought to go even further, both in higher energy and in type of particles to look for. In the midseventies, I became involved in a project that proposed to place a large detector on the bottom of the ocean at a depth of 4.8 kilometers off the southern (Kona) coast of the Big Island of Hawaii. It was called DUMAND, for Deep Undersea Muon and Neutrino Detector. The purpose was to open up a whole new window (“nu window”) on the universe by searching for very high-energy neutrinos from the cosmos, those with energies greater than 1 TeV (10¹² electron volts). The original leader of the project was Fred Reines, who would share the 1995 Nobel Prize for Physics for his codiscovery of the neutrino with Clyde Cowan in 1956.

It was theorized that very high-energy neutrinos would be produced by the enormous energy sources that exist at the centers of active galaxies. (See discussion of active galaxies in chapter 9.) Since they would likely come from deeper in the heart of the galaxy than photons, we hoped they would provide information about these great sources of energy. In 1984 I published a paper in Astrophysical Journal showing that active galaxies could produce detectable very high-energy neutrinos under certain conditions.¹⁰

The proposed technique is still basic to all the experiments in very high-energy astrophysics that are still being conducted, along with proton-decay experiments. When a charged particle is moving faster than the speed of light in a transparent medium (but still less than c) such as water or air, it emits an electromagnetic shock wave called Cherenkov radiation, which is a bluish light that is detectable with very highly sensitive photodetectors called photomultiplier tubes.

DUMAND was designed to deploy a large array of these photodetectors at the bottom of the ocean where the background light from cosmic-ray muons was minimal. The proton-decay experiments Kamiokande and IMB mentioned in chapter 11 also used this technique, installing photomultiplier tubes inside large tanks of very pure water in mines deep underground.

While working on DUMAND in the 1980s, I became involved in another experiment that I thought would provide complementary information useful for DUMAND. A team led by physicist Trevor Weekes of the Harvard-Smithsonian Center for Astrophysics had built a very inexpensive mirror ten meters in diameter made of flat plates forming a spherical reflecting surface at the Whipple Observatory on Mount Hopkins in Arizona. At its focus were mounted several small photomultiplier tubes.

When a very high-energy gamma-ray photon hits the top of the atmosphere, it generates a shower of thousands of electrons and other charged particles that cascade toward Earth. The Whipple telescope was designed to detect the Cherenkov light produced by this air shower.

In 1989, after I had left the Mount Hopkins project to work on a similar experiment closer to home, on Mount Haleakala on Maui, Weekes and coauthors reported a highly statistically significant signal from the Crab Nebula.¹¹ The Crab is the remnant of a supernova that was recorded by Arab, Chinese, Indian, and Japanese astronomers in 1054.

The Crab always had been our most likely candidate and we watched it closely. In 1968, a rotating pulsar had been discovered in the center of the nebula and identified as a neutron star. With its rapid rate of rotation, once every 33.5 milliseconds, the neutron star's magnetic field can accelerate electrons to very high energy. When they collide with the surrounding gas, they generate gamma-ray photons, and, I hoped, also neutrinos.

The Crab is within our galaxy. In 1992, Weekes and company reported a detection of an extragalactic source, the blazar Markarian 421. My graduate assistant Peter Gorham and I had also regarded blazars as promising sources since their beams point toward Earth.

In the meantime, a German group installed another gamma-ray telescope called HEGRA (High Energy Gamma Ray Astronomy) in the Canary Islands. It confirmed the Whipple sources in 1996 and in April 1997 reported the detection of another blazar, Markarian 501.12

So the upper limit of the energy spectrum of observed signals from the cosmos was moved up another order of magnitude above EGRET, at a monetary cost many orders of magnitude less, I might add.

Yet these trillion-electron-volt photons, eighteen orders of magnitude more energetic than the radio photons detected by the VLBA, are not the highest-energy objects observed in the universe. With arrays of particle detectors spread over large areas on Earth, showers of particles produced by cosmic rays hitting the atmosphere, primary cosmic rays up to 1 ZeV = 10²¹ eV have been observed.

But, there is a limit, called the Greisen-Zatsepin-Kuzmin limit, of 0.5 ZeV for cosmic-rays particles to make their way across the universe. Above that limit they will lose energy by collisions with the CMB. Thus, these ZeV particles likely come from fairly close to Earth. One possibility is Messier 87 in the constellation Virgo, which is “only” fifty-three million light-years away and has an active nucleus that is believed to contain a supermassive black hole.

On the other hand, note that very high-energy neutrinos are not subject to this limit and are the only known method by which we can observe such energies at great distances.

At this writing, the nu window on the universe has been opened with the 1987 supernova and now some exciting new results at much higher energies. However, after a huge effort involving a number of very challenging and expensive ocean deployments of test instruments, DUMAND was determined to be technically too difficult and in 1995 was canceled by its funding agency, the US Department of Energy. Nevertheless, DUMAND did serve as a proving ground for the concept of very high-energy neutrino astronomy, and a number of other similar projects have been developed that built on what we learned. As we will see in the next chapter, these are beginning to bear fruit with the report in 2013 of the observation of twenty-eight neutrinos above 30 TeV in an experiment at the South Pole.

NEUTRINO MASS

Neutrinos from the sky still made headlines in 1998 when Super-Kamiokande provided the first conclusive evidence that neutrinos have mass. I played a small role in this experiment, which was my last research project before retiring in 2000. However, I had worked on neutrino physics and astrophysics for over two decades and the technique used for this discovery was one I suggested at a neutrino-mass workshop in 1980 and published in the proceedings.¹³

Neutrinos with nonzero mass were predicted to have a property known as neutrino oscillation. The three types of neutrinos listed in table 11.1 and their antiparticles are produced by weak decay processes, such as beta decay,

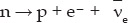
where 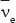is an antielectron neutrino. However, these neutrinos do not have definite masses. The quantum state of each is a mixture of three other neutrino states that have definite mass, denoted ν₁, ν₂, and ν₃. The masses (rest energies) are different so that the wave function describing a beam of each will have a different frequency. Because of this difference, the mixture changes as time progresses. Suppose we start with a pure beam of ν_μ's. The mixture changes with time so that when we detect a neutrino there is some probability that it will be one of the other types, ν_e or ν_τ. Neutrino oscillation does not occur when the masses are zero, so our observation of neutrino oscillation was direct evidence for neutrino mass.

High-energy cosmic-ray protons and other nuclei hitting the upper atmosphere produce copious amounts of short-lived pions and kaons. Their decay products include substantial numbers of muon and electron neutrinos, plus fewer tauon neutrinos. To reach the Super-K detector underground, a neutrino coming straight down from the top of the atmosphere travels about fifteen kilometers. By contrast, a neutrino passing straight up from the opposite side of Earth travels about thirteen thousand kilometers, so it has more time to oscillate.

Super-K observed an up-down asymmetry of muon neutrinos that was almost 50 percent at the highest energy of 15 GeV. Applying the theory of neutrino oscillations, this implied a difference in the mass-squares of two neutrino species to be in the range 5 × 10^–4 to 8 × 10^–3 eV².14

Additional experiments have pinned down the mass differences between neutrinos and determined that at least one has a mass on the order of 0.1 eV. This is to be compared with previously lightest known particle with nonzero mass, the electron, whose mass is 5.11 × 10⁵ eV, ten million times greater.¹⁵

Also in 1998, Super-K provided a neutrino photograph of the sun, shown in figure 13.3, taken at night through the earth—the first glimpse anyone has ever had of the core of a star.¹⁶ For those who think that the sun disappears when it drops below the horizon at night, the picture proves it's still there.

Masatoshi Koshiba would share the 2002 Nobel Prize for Physics for his leadership of the Kamioka experiments.

Figure 13.3. The sun at night, as seen through Earth in neutrinos by Super-Kamiokande. Image from R. Svoboda, UC Davis (Super-Kamiokande Collaboration).

DARK MATTER

As we have seen, one of the biggest problems with the original big-bang model was that if at the earliest operationally definable moment in our universe the average mass density of the universe were greater than the critical density by more than one part in 10⁶⁰, it would have immediately collapsed. If it had been lower by that amount, it would have expanded so rapidly that the current universe would be essentially empty. This was called the flatness problem since it required that the geometry of the universe be almost exactly Euclidean. Inflation solves the flatness problem by expanding space by many orders of magnitude so it became flat and the density became critical.

However, astronomers have long known that the density of visible matter of the universe, most of which is in luminous stars and dust, was far less than critical. Although reasonably good evidence for a large invisible component to the universe called dark matter goes back to the 1930s, most astronomers were slow to accept its reality for the very reasonable reason that they didn't see it directly with their telescopes. Missing mass was inferred by applying Newton's laws of motion and gravity to the observed orbital motions of stars in galaxies.

Maybe, some thought, these laws had to be modified on astronomical scales and some specific models were proposed. Ockham's razor, however, favors not rushing in to replace an existing theory—especially one so firmly ensconced as Newton's law of gravity—unless there is no other choice. And, so far, dark matter is the most parsimonious choice.17 Note that, while Newton's law of gravity is superseded by general relativity, this does not change the conclusions about missing mass since Newton's law still applies in this case.

Still, there were problems to be solved if dark matter and inflation were going to survive. As described in chapter 9, the remarkable success that big-bang nucleosynthesis had in calculating the exact abundances of the light nuclei, especially deuterium, showed that the density of baryons, that is, familiar atomic matter, is at most 5 percent of the critical density. This includes not only luminous matter, which (galaxies and all) is a miniscule 0.5 percent, but also all the bodies made of atoms (planets, brown dwarfs, black holes) that do not emit detectible light. Dark matter is not just dark—it is not matter as we know it.

Since dark matter must be electrically neutral, stable, and weakly interacting in order to have remained undetected, only neutrinos among the known elementary particles are possible candidates for the dark-matter particles. They are not baryons.

Two types of dark-matter models have been generally considered: hot dark matter where the particles are relativistic, that is, travel at speeds close enough to light that they must be described by relativistic kinematics; and cold dark matter where the particles are nonrelativistic. However, we should still keep open an in-between possibility: warm dark matter. In the case of hot dark matter, the gravitational mass of the dark-matter particles essentially equals the particle's kinetic energy since the rest energy is negligible. For cold dark matter, the gravitational mass essentially equals the particle's inertial mass since the kinetic energy is negligible. The temperature, that is, average kinetic energy of dark matter, should be the same as that of the CMB, since they are in equilibrium and generate no heat of their own, although the relic cosmic neutrino background (CνB) is slightly cooler at 1.95 K. For warm dark matter, neither mass contribution can be neglected. However, since the temperature of the universe changes so rapidly, on the cosmic timescale, there is usually a rapid transition from hot to cold for any given particle.

Neutrinos were early candidates for hot dark matter. As we saw in the previous section, the mass of at least one neutrino is no more than 0.1 eV, the rest are even lower. So whether cosmic neutrinos are either hot or cold depends on their temperature. The transition from hot to cold occurred at about a million years after the big bang. Earlier a neutrino of this mass is hot; later it is cold.

However, the number of neutrinos with this mass needed to provide an appreciable fraction of the critical density at that mass is something like 10⁹⁰, an unlikely number. By comparison, there are “only” 10⁸⁸ relic neutrinos, about the same number as photons in the CMB. The number of atoms is a billion times less. Thus, dark matter composed of familiar light neutrinos is pretty much ruled out from the latest CMB data, so we need to look for other dark-matter candidates. And, the proper sequence to follow is to examine first those possibilities that require the fewest new hypotheses.

While the standard model contains no candidates, there are two that do not require a complete overhaul of the theory but require only minor extensions: sterile neutrinos and axions.

Once it was discovered that the known neutrinos had mass, it was understood that they must be accompanied by another set of neutrinos not yet observed. It is conjectured that the additional neutrinos are sterile, that is, interact only gravitationally or at best very weakly. If they have appreciable mass, say more than a few hundred electron volts, then they are dark-matter candidates that still fit within the existing physics of the standard model, slightly extended to include parameters describing these states.18

While this book was in production, a variety of new observations had suddenly pushed sterile neutrinos to the forefront of the search for dark matter. This will be discussed in chapter 14.

Another hypothetical dark-matter candidate that still fits within the basic framework of the standard model is the axion, which was introduced back in 1977 to solve some technical problems with quantum chromodynamics. They are estimated to have masses less than 1 eV.

WIMPS AND SUSY

No other cold dark-matter candidate exists within reach of only minor changes in the standard model. If not a sterile neutrino or axion, it then has to be something totally new. Generically dubbed WIMP for Weakly Interacting Massive Particle, it most likely would be massive and nonrelativistic.

For a long time, the favorite candidate among physicists has been one of the particles predicted by an extension of the standard model that includes supersymmetry (SUSY), described in chapter 11. A generic term used for the WIMP that would arise from supersymmetry is neutralino. Four possible neutralinos are proposed that are the fermionic spartners of the gauge bosons of the standard model.

Evidence for SUSY was fully expected to be uncovered during the first runs of the LHC. It was not. Much of the theoretical effort over the last forty years has been based on supersymmetry, in particular, most theories of quantum gravity (super gravity) and M-theory. These could come crashing down if SUSY is not confirmed during the next run starting in 2015.

If this happens, many physicists will be disappointed, but not all—including me. Major discoveries in physics usually lead to simpler theories with fewer adjustable parameters. SUSY roughly doubles the number of adjustable parameters, and M-theory has 10⁵⁰⁰ different variations.19 Despite their mathematical beauty, that makes them ugly in my empirical mind.

Now, these were not the only problems that confronted cosmologists as the second millennium of the Common Era drew to a close. By 1998 it had been established that dark matter, whatever its nature, can at most contribute about 25 percent toward making the density of the universe critical. Three-quarters of the mass of the universe required by inflation was still missing. Once again, inflation was on the verge of being falsified. And, once again, nature came to its rescue.

DARK ENERGY

Since Hubble first plotted the recessional speeds of galaxies against their distances in 1929, astronomers steadily improved their measurements, but their data continued to fit a straight line. That is, the slope of the line, H, which gives the rate of expansion of the universe, appeared constant. Indeed, it was called the Hubble constant.

However, there was no reason for H, the expansion rate, to be constant. At some point the graph was expected to start curving downward as the expansion was slowed by mutual gravitational attraction. That is, the expansion should decelerate.

On the other hand, in 1995 cosmologists Lawrence Krauss and Michael Turner pointed out that existing data at the time suggested that the universe had a positive cosmological constant that, in fact, contributes the bulk of the critical density. They noted that this should produce an accelerated expansion that shows up as an increase in recessional speed at greater distances, that is, the graph should curve up.²⁰

The possibility of a positive cosmological constant had been mentioned earlier, in 1982, by the distinguished French astronomer Gérard de Vaucouleurs.21 He noted that the spatial distribution of quasars indicated a small positive curvature that could result from a positive cosmological constant.

As we will now see, later observations confirmed this effect, but until then the conclusions of these papers were not widely appreciated or accepted.

The recessional speeds of galaxies are easy to measure from their redshifts. But, as we have seen, measuring distances has always been a challenging problem for astronomers. In the 1990s, two research groups applied a new standard candle based on a special kind of supernova that involves a white dwarf. This method greatly improved the accuracy of estimated distances to galaxies at the greatest distances.

White dwarfs are the remnants of relatively typical stars (such as our sun) that have burned all their nuclear fuel. What dim light they still give off results from stored thermal energy. If a white dwarf has mass less than 1.38 solar masses, it will remain relatively stable. However, if it is part of a binary system, it can accrete matter from its companion and gain sufficient mass to explode as a supernova. This is called a Type Ia supernova. Because the explosion occurs when a unique mass is reached, the peak luminosity of the explosion will be about the same for all such events.

From energy conservation, light from the supernova will fall off with the square of distance. So, by measuring the observed brightness of a Type Ia supernova, identified by its light curve (variation of brightness with time), its distance can be determined with unprecedented precision.

One of the research groups was called the High-Z Supernova Search Team, led by Brian Schmidt of the Australian National University and Adam Riess of the NASA Space Telescope Science Institute. It included twenty-five astronomers from Australia, Chile, and the United States who analyzed observations from the European Southern Observatory in La Silla, Chile.

The other group, led by Saul Perlmutter of the Center for Particle Astrophysics at the University of California, Berkeley, was called the Supernova Cosmology Project and included thirty-one scientists from Australia, Chile, France, Spain, Sweden, the United Kingdom, and the United States. They analyzed data from the Calán/Tololo Supernova Survey performed at the Cerro Tololo Inter-American Observatory, also in Chile.22

In September 1998, the High-Z group published evidence that the Hubble curve was turning up at large distances.²³ On June 1, 1999, the Supernova Cosmology Project published its results that it interpreted as evidence for a positive cosmological constant with 99 percent confidence.

The High-Z results are shown in figure 13.4. The top panel shows a measure of distance used by astronomers called the distance modulus, which is based on the measured and expected luminosities, plotted against the redshift z, which measures the recessional velocity. The data are compared with three models assuming different values of Ω_M, the energy density of matter, and Ω_Λ, the energy density of the vacuum, each as a fraction of the critical density. The lower panel gives the difference between the measured distance modulus and its expected value a model with Ω_M = 0.2 and Ω_Λ = 0. While the error bars on individual points are large, the data as a whole clearly favor a model dominated by vacuum energy rather than matter. Matter domination would make the data curve downward, as the mutual gravitational attraction of galaxies at great distances would cause them to recede more slowly. Instead we witness a speeding up, indicating gravitational repulsion. That is, the expansion of the universe is accelerating. The source of that repulsion was been termed dark energy, with an energy density estimated by these data to be about 70 percent of critical density.

Now, this would seem to violate conservation of energy. However, it does not. Recall from chapter 5 that the first law of thermodynamics is basically a generalized form of conservation of energy that applies to any material system—gas, liquid, solid, or plasma. Familiarly, an expanding gas does work, as in the cylinders of your car (assuming it has an internal-combustion engine). That's because most gases have positive pressure caused by the motions of its molecules and their collisions with the walls of the container.

However, according to general relativity the pressure induced by a positive cosmological constant is negative. This means that the work done by this pressure as the volume expands is negative. Unlike the familiar expanding gas, an expanding universe with negative pressure does work on itself. Since the amount of work equals the increase in internal energy, conservation of energy is preserved.

Perlmutter, Riess, and Schmidt would share the 2011 Nobel Prize for Physics for the dramatic proof that the universe is falling up.

As mentioned, this discovery was not totally surprising. It was well known to cosmologists that a positive cosmological constant, introduced by Einstein in his general theory, provides for gravitational repulsion. Indeed, we have seen that a de Sitter universe, which has no matter or radiation and just a positive cosmological constant, expands exponentially and offers a simple model for inflation in the early universe. Now we seem to have inflation going on today as well, albeit considerably slower.

Let us look briefly at the physics involved. The cosmological constant (see chapter 6) is equivalent to a scalar field of constant energy density uniformly filling the universe. Thus, as the universe expands, its total internal energy increases as its volume increases.

While the accelerating expansion of the universe could be the result of a cosmological constant, it need not be. Alternatively, the universe might be filled with a quantum field that has negative pressure. This field has been termed quintessence. Negative pressure is not unheard-of in other branches of physics. For certain ranges of pressure and temperature, a Van der Waals gas has negative pressure when its molecules are so close to one another that their electron clouds push away from each other and the molecules experience a net attraction.

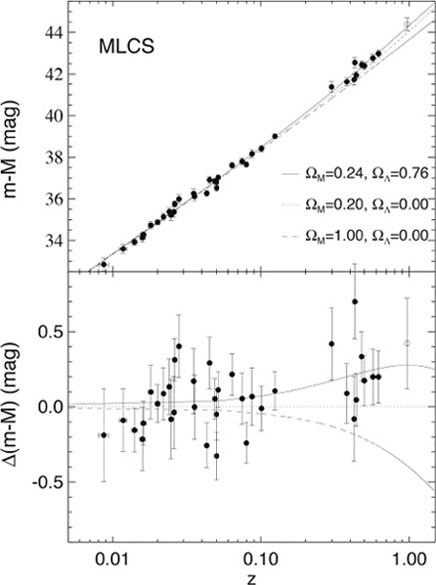
Figure 13.4. Results from the High-Z supernova search experiments. Image from Adam G. Riess et al., “Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant,” Astronomical Journal 116, no. 3 (1998): 1009. © AAS. Reproduced with permission.

The quanta of the quintessence field would be bosonic, most likely spin-zero. It would be expected to have negative pressure by virtue of the quantum mechanical tendency of bosons to collect in a single state. The possibility of quintessence is included in the most advanced cosmological models by not automatically assuming a cosmological constant is the source of the acceleration.

THE COSMOLOGICAL-CONSTANT PROBLEM

In 1989, Steven Weinberg pointed out what he called “the cosmological-constant problem.”24 Because of the uncertainty principle, a quantum harmonic oscillator has a minimum energy that is not zero because it can never be brought exactly to rest. The lowest energy level has a zero-point energy.

A quantum field is mathematically equivalent to a quantum harmonic oscillator. So, if you take a quantum electromagnetic field, for example, and remove all its quanta (photons), you will still have energy left over even though no photons are present. Weinberg associated the energy density implied by a cosmological constant with the quantum zero point energy of the vacuum. When he made the calculation, it turned out to be 120 orders of magnitude greater than the highest possible value it could have and be consistent with observations.

Actually, Weinberg only considered photons, which are bosons. Fermions have a negative zero-point energy, so that will cancel some of the positive energy from bosons. That cancellation would be perfect if the universe were supersymmetric. But it is not—at least at low energies. So, the discrepancy is still fifty orders of magnitude. This is the cosmological-constant problem.

Any calculation that is so far from what is observed is surely wrong, and there are many proposed solutions. I discussed several in The Fallacy of Fine-Tuning,²⁵ but none have satisfied a consensus of physicists. Nevertheless, it is clear to me why the calculation is wrong.

The calculation of the energy density of the vacuum involved a sum over all the quantum states in a volume of space. However, the maximum number of states in a volume is equal to the number of states of a black hole of the same volume. And it is easy to show that the number of states of a black hole is proportional to the surface area of the black hole, not its volume. When you do the calculation by summing the states on the surface rather than the volume, you get a value consistent with observation.

BACK TO THE SOURCE

As we have seen, the CMB we observe today was produced when atoms were formed 380,000 years after the big bang and photons decoupled from the rest of matter. At that time, that surface contained the ripples in density that evolved from the original source over that period. Since then the universe has expanded by a factor of 1,100 and the radiation has cooled from 3,000 K to 2.725 K.

In CMB anisotropy observations, investigators measure temperature differences between two directions in the sky separated by an angle θ. When they look at the CMB in two regions of the sky separated by θ = 180^o and find a temperature difference, this is called a dipole anisotropy. Recall that this particular anisotropy, which results from our motion relative to the CMB, was observed by Smoot and his team when they flew their original differential microwave radiometer onboard the U-2 spy plane in 1976. This effect is subtracted out for the analysis of the early universe.

When investigators look at four regions separated by 90^o and see different temperatures, they have a quadrupole anisotropy. This has a background contribution from the Milky Way and is also ignored. In general, for a separation angle θ_ℓ in degrees we have a multipole index ℓ = 180/θ_ℓ and, as we will see, the higher poles, that is, smaller angles, are the most important.

When the square of the fractional temperature difference is plotted against ℓ we have what is called the angular power spectrum. Theoretical analyses and computer simulations are able to use these measurements to reconstruct the acoustic power spectrum produced by the primordial fluctuations. With its limited angular resolution of 7^o, COBE was only able to explore out to about ℓ = 20. However, this was sufficient to verify that the fluctuations had at least the approximate scale invariance predicted by inflation. Calculations predicted that at angles less than 1^o or ℓ greater than about 200 one should start observing peaks in the angular spectra that correspond to harmonics in the original acoustic oscillations (see chapter 11).

JUMPING ON THE BANDWAGON

Even before the COBE results were announced, research groups from all over the world rushed to hop on the bandwagon of what was recognized as a one of the greatest scientific opportunities ever presented—the ability to look back to the first moments of universe. On its Lambda website devoted to CMB science, NASA lists twenty experiments in operation during the 1990s using either ground-based telescopes or high-altitude balloons designed specifically to measure the anisotropy.²⁶

Most had angular resolutions much better than COBE's 7 degrees, although they were unable to collect the amount of data that a satellite in orbit can. The Canadian SK telescope in Saskatoon, Saskatchewan, had an angular resolution from 0.2^o to 2^o in six frequency bands between 26 and 46 GHz enabling it to cover the range ℓ = 54 to 404.²⁷

Even more impressive was ACTA, the Australia Telescope Compact Array composed of five twenty-two-meter-diameter antennas 30.6 meters apart in an East–West line. Its angular resolution was a remarkable 2 arcminutes (0.03 degrees) at a frequency of 8.7 GHz and covered ℓ = 3350 to 6050.²⁸ These experiments gave the first hints that much more was to be learned from the CMB, in particular, that the spectrum was not flat at smaller angles.

Although it would be quicker for me at this point to jump to the latest results, in this chapter and the next I am going to present a chronological series of plots of increasing precision both to demonstrate how science works and to give deserved credit to those who pioneered in this remarkable advance.

Figure 13.5 shows the status as of 1998 of the angular spectrum up to ℓ = 1000 obtained by seventeen experiments.²⁹ There the first signs of the first (fundamental) acoustic peak can be seen.

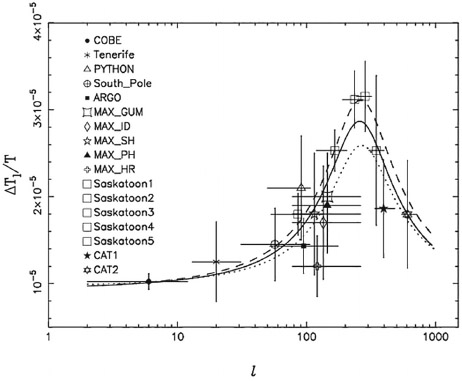
Figure 13.5. A compilation of the CMB angular anisotropy data as of 1998. Image used by permission of Oxford University Press, from S. Hancock et al., “Constraints on Cosmological Parameters from Recent Measurements of Cosmic Microwave Background Anisotropy,” Monthly Notices of the Royal Astronomical Society 294, no. 1 (February 11, 1998): L1–L6.

At the time, two exceptional experiments using high-altitude balloon flights, called BOOMERANG and MAXIMA were gathering data that greatly improved the spectrum. We will hear about their results and those of the even more spectacular Wilkinson Microwave Anisotropy Probe (WMAP) and then the Planck space telescope in the next chapter.

And so, the second millennium of the Common Era ended with convincing evidence that our universe began with a rapid exponential expansion called inflation that ended after about 10^–32 second. After a few billion years of more sedate expansion, our universe is now once again inflating exponentially, albeit at a much slower rate that is likely to continue forever. At some point in the far future, any inhabitants on a planet still heated by a sun will be unaware of anything else in the universe beyond the Milky Way and the Andromeda halo from when the two merged, since the rest will be beyond their horizon.