THE VISIBLE UNIVERSE

Astronomy in the 1970s was headlined by the space program, with the first manned moon landing by Apollo 11 on July 20, 1969, followed by five more, ending with Apollo 17 on December 11, 1972. The unmanned vehicles Voyager 1 and 2, launched in 1977, visited Jupiter and Saturn before continuing into the outer solar system and are now entering interstellar space. In 1974, Mariner 10 passed Venus and visited Mercury. In 1976, the Viking spacecraft landed on Mars.

The International Ultraviolet Explorer (IUE) was launched in 1978 to observe astronomical objects in the UV region of the spectrum, which is impossible from Earth because of atmospheric absorption. Lasting almost eighteen years, IUE made over 104,000 observations of every kind of object, from planets to quasars.

Three satellites in the NASA High Energy Astronomy Observatory program explored three additional new windows on the cosmos: x-rays, gamma rays, and cosmic rays. HEAO 1, launched in 1977, surveyed the x-ray sky and discovered 1,500 sources. HEAO 2, launched the following year and renamed the Einstein Observatory, was an x-ray imaging telescope that discovered several thousand more sources and pinpointed their locations. The principal investigator of the Einstein project, Riccardo Giacconi, had previously led a team that in 1962 discovered a strong x-ray source that was designated Scorpius X-1 and was later identified as a neutron star. Its x-ray emission is ten thousand times as powerful as its optical emission. Giacconi would receive the 2002 Nobel Prize for Physics. HEAO 3, launched in 1979, measured the spectra and isotropy of x-ray and gamma-ray sources and determined the isotopic composition of cosmic rays.

On the ground, new large reflecting telescopes materialized on mountaintops in Arizona, Chile, Australia, Hawaii, and Russia. The photographic plate was gradually replaced by the charge-coupled device (CCD) as the main detector, greatly improving photon-collection sensitivity and efficiency while enabling automatic digital readouts. The new high-speed digital computers processed data rapidly and in large quantities, and provided automatic control of the mirrors. No longer would astronomers have to spend long, cold hours in the cages of their telescopes, manually keeping them pointed at their targets.

By decade's end, the collection area of telescopes was increased above what was possible with a single mirror by connecting many mirrors together with computers synchronizing the light gathered. The first such device, called the Multi-Mirror Telescope (MMT), was operating on Mount Hopkins in Arizona at the time I was collaborating on another project on the mountain measuring very high-energy gamma rays.

During my years at the University of Hawaii I witnessed the steady installation of international telescopes on Mauna Kea, the 13,796-foot mountain on the Big Island of Hawaii, creating the finest ground-based astronomical site in the world. Because of its high altitude with exceptionally dry air above, Mauna Kea not only is a superior location for observations in the visible band but also enables the infrared sky to be explored as well.

I have no need to catalog, nor can I give justice to, the spectacular observations made with these wonderful instruments. The photographs that fill astronomy books and NASA's web sites demonstrate that nature can compete with any human art form or religion in creating awe and beauty. For my purposes at this point, it suffices to say that the contrast between luminous matter in the universe and the CMB could not be starker. The optically visible universe is complex, varied, and irregular. To one part in one hundred thousand, the CMB is simple, smooth, and regular. To that level of precision, it requires only one number to describe—its temperature, 2.725 K. Yet it would turn out that observations of the tiny CMB deviations from smoothness would tell us how all these complex wonders came about.

THE STRUCTURE PROBLEM

Long before the discovery of the CMB, astronomers puzzled over the origin of the structure in the universe. The prominent British physicist and astronomer James Jeans had worked out the mechanism by which a smooth cloud of gas will contract under gravity to produce a dense clump. He derived an expression for the minimum mass at which gravitational collapse overcomes the outward pressure of the gas. Called the Jeans mass, it depends on the speed of sound in the gas and the density of the gas.

The Jeans mechanism worked fairly well for the formation of stars, but not for galaxies. In 1946, Russian physicist Evgenii Lifshitz extended Jeans's calculation to the expanding universe and proved that gravitational instability alone is unable to account for the formation of galaxies from the surrounding medium.1 Basically, expansion combines with radiation pressure to overwhelm gravity. The failure to understand galaxy formation remained a bugaboo in astronomy until the 1980s.

When the decade of the 1970s began, a number of authors proposed that fluctuations in the density of primordial matter in the early universe acted to form the galaxies. Since the pressure of a medium is related to its density by an equation of state, density fluctuations produce pressure fluctuations that are just what we call sound. You often hear it said that “big bang” is a misnomer, since explosions in space make no noise. Well, in fact, the big bang did make an audible bang.

As first pointed out by Pythagoras, the sounds from musical instruments can be decomposed into harmonics where each harmonic is a pure sound of a single frequency or pitch. The same is true for any sound, although the harmonics are usually not so pure as with musical instruments. The distribution of sound intensity among the various frequencies is given by its power spectrum.

A mathematical method called Fourier transforms, developed by the great French mathematician Jean Baptiste Fourier (1768–1830), is widely used by physicists and engineers in many applications besides sound. The Fourier transform enables one to take any function of spatial position or time and convert it to a function of wavelength or frequency. If the function is periodic in space or time, the spectrum contains peaks at specific wavelengths or frequencies.

In the 1970s, Edward Harrison2 and Yakov Zel’dovich³ independently predicted that the spectrum of sounds produced by density fluctuations in the universe should exhibit a property known as scale invariance. In general, scale invariance is a principle that is applied in many fields from physics to economics. It refers to any feature of a system that does not change whenever the variables of the system are changed by the same factor. For example, Newton's laws of mechanics do not change when spatial units are converted from feet to meters. Scale invariance is another symmetry principle.

But scale invariance does not always apply. Given similar structure and biology, the height an animal can jump is almost independent of how big the animal is. That is, it does not scale. This is known as Borelli's law, proposed by Giovanni Alfonso Borelli (1608–1679). In his 1917 classic On Growth and Form, D’Arcy Wentworth Thompson wrote, “The grasshopper seems as well planned for jumping as the flea…but the flea's jump is about 200 times its own height, the grasshopper's at most 20–30 times.”⁴

Although they put it in more technical terms in their papers, Harrison and Zel’dovich basically pointed out that the density fluctuations inside the horizon of the universe must be independent of the scale of the universe as the universe expands. If the density fluctuation were greater at either an earlier time or at a later time, parts of the universe would collapse into black holes.

The Harrison-Zel’dovich power spectrum is expressed in terms of the wave number (also called the spatial frequency) k = 2π/λ, where λ is the wavelength. (Do not confuse this k with the cosmic curvature parameter k). The power spectrum is assumed to be proportional to kⁿ, where n is the spectral index. Scale invariance requires n = 1.

Now, how could we expect to “listen” to those primordial sounds? In 1966, after the discovery of the cosmic microwave background, Ranier Sachs and Arthur Wolfe showed that density variations in universe should cause the temperature of the CMB to fluctuate across the sky as photons traveling through higher gravitational potentials are redshifted and those moving through lower potentials are blueshifted.5

Sachs and Wolfe weren't thinking of primordial fluctuations, but in one of the most remarkable achievements in scientific history, it would turn out that the CMB would be able to read those primordial fluctuations all the way back to when the universe was only 10^–35 second old and observe exactly how the galaxies and other lumps of matter came together billions of years later as a consequence of these fluctuations. It was estimated that to account for galaxy formation the fractional variation from temperature of the currently observed radiation must be at least ΔT/T = 10^-5.⁶

GRAVITATIONAL LENSING

One of the dramatic predictions of general relativity was the deflecting of light by the gravitational field of the sun. In 1936, Einstein pointed out that light bent by astronomical bodies could produce multiple images. In 1937, Fritz Zwicky suggested that a cluster of galaxies could act as a gravitational lens. However, it was not until 1979 that astronomers at the Kitt Peak Observatory in Arizona observed the effect. They photographed what appeared to be two quasars unusually close to one another with the same redshift and spectrum, which indicated they were actually the same object. Many examples of lensing have since been identified.

In 2013, a telescope at the South Pole called, appropriately enough, the South Pole Telescope, observed a statistically significant curl pattern called B-Mode in the polarization of the CMB that results from the lensing of the intervening structure in the universe.7 This observation was confirmed in 2013 and 2014 by an experiment in Chile called POLARBEAR.⁸ We will talk more about gravitational lensing in chapter 14 and also discuss the latest results from the South Pole on gravitational waves, which also involved the detections of B-mode polarization in the CMB.

THE INVISIBLE UNIVERSE

We have seen how astronomers in the 1930s discovered that there was a much larger amount of matter in the universe than could be accounted for by the luminous matter—stars and hot gas—in galaxies. Observations just did not agree with Newton's laws of mechanics and gravity, but few were ready to say these were in any sense invalidated. Fritz Zwicky had dubbed this invisible gravitating stuff dunckle materie, or dark matter.

Not much was done on the question until the 1970s when radio astronomers in Groningen, Netherlands, studied the 21-centimeter hyperfine spectral line emitted by neutral hydrogen molecules from various galaxies. Their measurements showed flat rotation curves for a large sample of galaxies.⁹ In a rotation curve, one graphs the rotational speeds of stars, which Doppler-shifts the observed spectral line, against their distances to the center of their galaxies. By Newton's laws, these should fall off for stars farther from the center, just as the speeds of the planets in the solar system fall off with distance from the sun, where most of the mass of the solar system is located. Instead the speeds remained largely constant.

The explanation for this observation was that the galaxies have halos of unseen dark matter that extend well beyond the denser regions nearer the centers that give off light. This invisible matter is hardly negligible. In fact, we now know it constitutes 90 percent of the masses of the galaxies studied. As we will see in a later chapter, the gravitational lensing described in the previous section has been used to provide direct evidence for the existence of dark matter.

In the meantime, American astronomer Vera Rubin and her collaborators were making a systematic study of the rotations of spiral galaxies in the optical spectrum and observing the same effect.

Astronomers were well aware that many astronomical bodies do not directly emit much, if any, detectable light—for example, planets, brown dwarfs, black holes, neutron stars. However, it seemed unlikely that these were sufficient to account for the total mass inferred from Newtonian dynamics.

Furthermore, there was independent evidence that most of the dark matter could not be composed of familiar atomic matter but must be something not yet identified. This evidence came from the same source that we saw in chapter 10 provided strong confirmation of the big bang—big-bang nucleosynthesis.

In figure 10.4 we compared the theoretical and measured abundances of light nuclei as a function of Ω_B, the ratio of the baryon density to the critical density. While the precise numbers are still changing, the latest measurements indicate that Ω_B is less than 5 percent while 26 percent of the mass of the universe is dark matter that cannot be composed of familiar atoms.

THE RISE OF PARTICLE PHYSICS

The discovery of the CMB in 1964 coincided with the rise of the new field of elementary particle physics in which I participated, first as a graduate student at UCLA (University of California at Los Angeles) and, after receiving my doctorate in 1963, as physics professor for thirty-seven years at the University of Hawaii with visiting professorships at the universities of Heidelberg, Oxford, Rome, and Florence. Eventually particle physics would play an important role in cosmology, so let me redirect our attention for a moment from the very big to the very small.

Using particle accelerators of ever-increasing energy, and particle detectors of ever-increasing sensitivity, a whole new subatomic world was uncovered that culminated in the 1970s with the development of the standard model of elementary particles and forces. A place was found in this model for all these particles, which successfully described how they interact with one another.

On April 10, 2014, as this book was in production, the CERN laboratory in Geneva (European Organization for Nuclear Research) confirmed with high significance the existence of an “exotic” negatively charged particle called Z(4430), reported earlier by another collaboration. Stories in the media suggested a violation of the standard model. However, this is not the case. The Z(4430) is evidently composed of four quarks, the first of its kind. However, this no more refutes the standard model than the existence of the helium nucleus with four nucleons refutes the nuclear model.

Refer to table 11.1, which shows the elementary particles and their masses according to the standard model. The mass of each particle is given in energy units, MeV (million electron volts) or GeV (billion electron volts), which is just the rest energy of the particle, equivalent to its mass by E = mc² since c is just an arbitrary constant.

Consider the group of particles labeled fermions. These all have intrinsic angular momentum, or spin, of ½.¹⁰ They are found in three “generations,” the columns headed by u, c, and t. Each generation has two quarks and two leptons. The first generation on the left is composed of a u quark with charge +2e/3, where e is the unit electric charge, and a d quark with charge –e/3. Below the quarks are the first generation leptons: the electron neutrino ν_e, which has zero charge, and the electron e, which has charge –e. Each of the fermions is accompanied by an antiparticle of opposite charge, not shown in the table. (Antineutrinos, like neutrinos, are uncharged.)

I will discuss the masses of neutrinos in chapter 13. For now, suffice it to say that at least one neutrino has a mass on the order of 0.1 eV. This is to be compared with the next lightest nonzero mass particle, the electron, whose mass is 511,000 eV.

Table 11.1. The particles of the standard model. The masses are given in energy units. Antiparticles and the Higgs boson are not shown.

The second and third generations have a similar structure of quarks and electrons, except they are all heavier and unstable, decaying rapidly into lighter particles. For example, the muon, μ^–, with a mean lifetime of 2.2 microseconds, is essentially just a heavier electron with a mass of 106 MeV. Its main decay process is

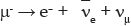
where 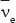is an antielectron neutrino. The antimuon, μ⁺, has a similar decay:

Note that the t quark is 184 times as massive as the proton (mass 938 MeV).

The standard model contains three forces: electromagnetism, the weak nuclear force, and the strong nuclear force. Gravity, which has a negligible effect at the subatomic level and is already well described at the large scale by general relativity, is not included. Only when we get down to the Planck scale, 10^–35 meter, does general relativity break down. We will talk about that later.

The particles in the column on the right of table 11.1 are the so-called mediators of the forces. They are bosons, which are defined as particles of integer spin. In this case, they all have spin 1. The bosons of the standard model are sometimes referred to as “force particles” because, in the quantum field theories of forces that are at the heart of the standard model, these particles are the quanta associated with the force fields. For example, the photon γ (for gamma ray) is the quantum of the electromagnetic field.

The force particles are usually pictured in the standard model as being exchanged between interacting quarks or leptons, carrying momentum and energy from one to the other. Figure 11.1 shows two electrons interacting by exchanging a photon. This is the canonical example of a Feynman diagram, introduced by physicist Richard Feynman in 1948.¹¹ Feynman diagrams are basically calculational tools and should not be taken too literally.¹²

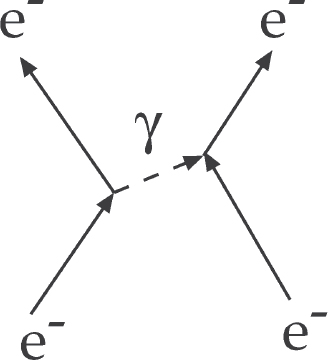
Figure 11.1. Feynman diagram showing two electrons interacting by exchanging a photon. Image by the author.

So, in the standard model, the photon is the force carrier of the electromagnetic force. All the elementary particles except neutrinos interact electromagnetically. The quantum field theory called quantum electrodynamics (QED) that successfully describes the electromagnetic force was developed in the late 1940s by Sin-Itiro Tomonaga, Julian Schwinger, Richard Feynman, and Freeman Dyson.13 The first three would share the 1965 Nobel Prize for Physics, which is limited to three honorees.

In figure 11.2, an electron and positron collide and annihilate into a Z-boson, which then re-creates the pair. These are just two examples of the many diagrams that describe particle interactions.

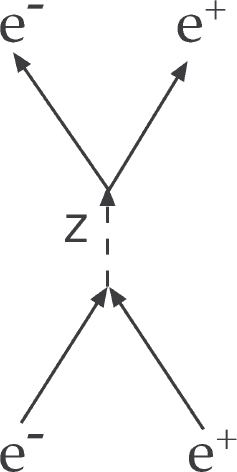
Figure 11.2. An electron and positron pair annihilating into a Z-boson that then re-creates the pair. Image by the author.

The W boson appears in two electrically charged states, +e and –e. Together with the Z boson, which has zero charge, these “weak bosons” mediate the weak nuclear force that acts on all elementary particles except the photon and the gluon. The gluon will be discussed in a moment.

The most familiar weak interaction is the beta decay of nuclei in which an electron and antineutrino are emitted. In the standard model, the fundamental process involves the quarks inside nucleons (protons and neutrons), which are themselves inside nuclei,

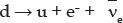
To see the role that the W boson plays, refer to figure 11.3.

Figure 11.3. The beta decay of the d quark. In this picture, the d quark decays into a W^– boson and a u quark. The W^– propagates a short distance in space (about 10^–18 meter) and then decays into an electron and an antielectron neutrino. Image by the author.

The particle labeled g in table 11.1 is the gluon. It is found in eight different states of what is called color charge, which is analogous to electric charge but comes in eight varieties that are metaphorically called “colors.” The gluon mediates the strong nuclear force responsible for holding nuclei together. Only quarks interact strongly. In the standard model, the strong force is described by a quantum field theory, dubbed by Feynman quantum chromodynamics.

Most of the hundreds of new particles that were discovered in the 1960s were strongly interacting particles. These are generically referred to as hadrons. Two types of hadrons were identified: baryons, which have half-integer spin and mesons, which have integer spin. The proton and neutron are baryons. The lightest meson is the pion or pi-meson, which comes on three charge states: π⁺, π⁰, and π^–. I did my doctoral thesis work on the K-meson or kaon, which comes in four varieties: K⁺, K^–, K⁰, . They are composed of quark-antiquark pairs where one of the quarks is an s or its antiparticle. I need not elaborate further.

All the hadrons except nucleons are highly unstable, some with lifetimes so short that they can barely traverse the diameter of a nucleus before decaying. The neutron is unstable to beta decay, with a mean lifetime of about fifteen minutes. Although containing neutrons, most nuclei are stable since energy conservation prevents them from disintegrating. You won't find many free neutrons (or other hadrons except protons) floating about in outer space now, apart from a few being produced momentarily by high-energy cosmic-ray collisions.

The proton is obviously highly stable or else we wouldn't have so much hydrogen in the universe after 13.8 billion years. However, as we will see shortly, the possibility of proton decay even with a very long lifetime has enormous cosmological implications.

The standard model of elementary particles and forces arose, in part, from the attempt to fit these many new particles into a simple scheme. It succeeded spectacularly. Here's the scheme: The baryons are all composed of three quarks. Antibaryons are composed of three antiquarks. Mesons are composed of a quark and an antiquark. No hadron has ever been observed that cannot be formed from the quarks in table 11.1 and their antiquarks.

The nuclei of the atoms that constitute familiar matter are composed of just u and d quarks. The proton is uud and the neutron is udd. Every physical object that we deal with in our everyday lives, and every object that scientists in all disciplines except particle physics and particle astrophysics deal with, is made of just three elementary particles: the u quarks and d quarks that compose atomic nuclei and the electrons that swarm in clouds around them to make atoms.

The discovery in 2012 of what is almost certainly the long-expected Higgs boson was the final icing on the cake for the standard model. The Higgs boson is a spin-zero particle, H, that is responsible for generating the masses of leptons and weak bosons. The quarks get some of their masses this way, but most by another mechanism involving the strong force that I need not get into. The photon and gluon are massless.

Let us now look at the theoretical ideas behind the standard model. We will see they go well beyond that specific example to our whole concept of the meaning of physical law.

SYMMETRY AND INVARIANCE

The central concepts of modern physics, from relativity and quantum mechanics to the standard model, are symmetry principles and the manner in which those symmetries are broken. These have greatly aided us in our understanding of both the current and the early universe.

Symmetry is related to another concept—invariance. A perfect sphere is invariant to a rotation about any axis. That is, it looks the same from every angle. So we say it possesses spherical symmetry.

If you take a spherical ball of squishy matter (like Earth) and start to spin it rapidly, it will begin to bulge at the equator and its spherical symmetry will be broken. However, the ball will still possess rotational symmetry about the spin axis.

Here I am less interested in the symmetries of geometrical objects than those embedded within the mathematical principles called the “laws of physics.” These are principles that appear in the models physicists devise to describe observations.

When an observation is invariant to some operation, such as a change in the angle at which the observation is made, then the model properly describing that operation must possess the appropriate symmetry. In particular, the model cannot assume an x, y, z–coordinate system in which the axes point in specific directions.

In the 1950s, it was shown that the weak nuclear force violates mirror symmetry, technically referred to as parity. That is, weak processes are not invariant to the interchange of left and right, just like your hands (or face, for that matter). Mathematically, an operator P, called the parity operator, changes the state of a system to its mirror image.

Particle physicists define another operator C that exchanges a particle with its antiparticle and an operator T that reverses time. In the 1960s, it was discovered that the combined symmetry CP is very slightly violated in the decay of neutral kaons. The combined symmetry CPT is believed to be fundamental. In that case, the violation of CP implies the violation of T. Direct T-violation has been empirically confirmed while CPT has never been violated in any observed physical process.

Note that T-violation is not to be interpreted as the source of the arrow of time since the effect is small, about 0.1 percent, and does not forbid time reversal. It just makes one direction in time slightly more probable than the other.

CPT invariance says specifically that if you take any reaction and change all its particles to antiparticles, run the reaction in the opposite time direction, and view it in a mirror, you will be unable to distinguish it from the original reaction. So far, this seems to be the case.

In short, not only do the laws of physics obey certain symmetries but a few (not all) can also violate some of these symmetries—usually spontaneously, that is, by accident.

By analogy, consider the teen party game “spin the bottle.” A boy sets a bottle spinning on a floor in the center of a circle of girls. The spinning bottle has rotational symmetry about a vertical axis. But when friction brings it to a halt, the symmetry is spontaneously broken and the bottle randomly points to the particular girl the boy gets to kiss.

SYMMETRIES AND THE “LAWS OF PHYSICS”

As described in chapter 6, in 1915 Emmy Noether proved that the three great conservation principles of physics—linear momentum, angular momentum, and energy—are automatically obeyed in any theory that possesses, respectively, space-translation symmetry, space-rotation symmetry, and time-translation symmetry. The conservation principles are not, as usually taught in physics classes and textbooks, restrictions on the behavior of matter. They are restrictions on the behavior of physicists. If a physicist wants to build a model that applies at all times, places, and orientations, then he has no choice. That model will automatically contain the three conservation principles.

While the standard model of elementary particle physics is a long way from Noether's original work, it confirmed the general idea that the most important of what we call the laws of physics are simply logical requirements placed on our models in order to make them objective, that is, independent of the point of view of any particular observer. In my 2006 book The Comprehensible Cosmos I called this principle point-of-view invariance and showed that virtually all of classical and quantum mechanics can be derived from it.¹⁴

The book's subtitle is: Where Do the Laws of Physics Come From? The answer: They didn't come from anything. They are either metalaws that are the necessary requirements of symmetries that preserve point-of-view invariance or bylaws that are accidents that happen when some symmetries are spontaneously broken under certain conditions. Note that if there are multiple universes, they should all have the same metalaws but probably different bylaws.

Although it is not widely recognized, Noether's connection between symmetries and laws can be extended beyond space-time to the abstract internal space used in quantum field theory. Theories based on this idea are called gauge theories. Early in the twentieth century it was shown that charge conservation and Maxwell's equations of electromagnetism can be directly derived from gauge symmetry.

In the late 1940s, gauge theory was applied to quantum electrodynamics, the quantum theory of the electromagnetic field that was described earlier. The spectacular success of this approach, which produced the most accurate predictions in the history of science, suggested that the other forces might also be derived from symmetries. In the 1970s, Abdus Salam, Sheldon Glashow, and Steven Weinberg, working mostly independently (they must have read the same papers), discovered a gauge symmetry that enabled the unification of the electromagnetic and weak forces into a single electroweak force. This was the first step in the development of the theoretical side of standard model. The three would share the 1979 Nobel Prize for Physics.

Let me explain what is meant when we say two forces are unified. Before Newton, it was thought (expressed in a modern context) that there was one law of gravity for Earth and another law for the heavens. Newton unified the two, showing that they are the same force, which described the motions of apples and planets in terms of a single law of gravity. In the nineteenth century, electricity and magnetism were thought to be separate forces until Michael Faraday and James Clerk Maxwell unified them in a single force called electromagnetism.

However, electromagnetism and the weak nuclear force hardly looked like the same force at the accelerator energies that were available until just recently. The electromagnetic force reaches across the universe, as evidenced by the fact that we can see galaxies that were over thirteen billion years away when they emitted the observed light. The weak force only reaches out to about a thousandth of the diameter of a nucleus. It took a mighty feat of imagination to think these might be the same force! I recall Feynman being particularly dubious.

In the Feynman diagram scheme, a force is mediated by the exchange of a particle whose mass is inversely proportional to the range of the force. Since the range of electromagnetism seems to be unlimited, its mediator, the photon, must have very close to zero mass. Indeed, the mass of a photon is identically zero according to gauge invariance. On the other hand, the particles that mediate the weak force must have masses of 80.4 and 90.8 GeV. That is, they are almost two orders of magnitude more massive than the proton (0.938 GeV).

According to the Salam-Glashow-Weinberg model, somewhere above about 100 GeV (now known to be 173 GeV), the electromagnetic and weak forces are unified. Below that energy, the symmetry is broken spontaneously, that is, by accident, into two different symmetries—one corresponding to the electromagnetic force and the other to the weak force. The photon remains massless while the three “weak” bosons—the W⁺ and W^–, which have electric charge +e and –e, respectively, and the neutral Z—have the masses implied by the short range of the weak force.

In the electroweak symmetry-breaking process, the weak bosons, as well as leptons, gain their masses by the Higgs mechanism that was first proposed in 1964 by six authors in three independent papers, published well before the standard model was developed: Peter Higgs of Edinburgh University, Robert Brout (now deceased) and François Englert of the University Libre de Bruxelles, Gerry Guralnik of Brown University, Dick Hagen of the University of Rochester, and Tom Kibble of Imperial College, London.15 To his embarrassment, the process was named after just one of the six, the unassuming British physicist Peter Higgs.

In the Higgs mechanism, massless particles obtain mass by scattering off spin-zero particles called Higgs bosons, and this became an intrinsic part of the standard model that was developed a decade later.

Basically you can think of it this way: The universe is a medium filled with massive Higgs particles that flit in and out of existence. As a zero-mass elementary particle tries to make its way through that medium at the speed of light, it bounces off the Higgs particles so that its progress through the medium is slowed down. This constitutes an effective increase in inertia, and mass is a measure of inertia.

The standard model predicted the exact masses of the weak bosons, 80.4 GeV for the Ws and 90.8 GeV for the Z. It also predicted the existence of weak neutral currents, mentioned in chapter 10 as playing a role in supernova explosions, which result from the exchange of the zero-charge Z boson. By 1983 these predictions had been spectacularly confirmed.

The full standard model containing both the strong and electroweak forces is based on a combined set of symmetries. The strong force is treated separately and is mediated, as mentioned, by eight massless gluons. The small range of the strong force, about 10^–15 meter, results from a different source than the masses of gluons, which are zero; but we need not get into that.

By the end of the twentieth century, accelerator experiments had produced ample empirical confirmation of the standard model at energies below 100 GeV and had provided measurements of its twenty or so adjustable parameters, in some cases with exquisite precision. The model has agreed with all observations made in physics laboratories in the decades since it was first introduced.

On July 4, 2012, two billion-dollar experiments involving thousands of physicists working on the LHC at CERN reported with high statistical significance the independent detection of signals in the mass range 125–126 GeV that meets all the conditions required for the standard model Higgs boson.¹⁶ Two of its six inventors, Peter Higgs and François Englert, shared the 2013 Nobel Prize for Physics.

Of course, as with all models, the standard model is not the final word. But with the verification of the Higgs boson and the availability of higher energies, we are now finally ready to move to the next level of understanding of the basic nature of matter—and, as we will see, deeper into the big bang. The LHC is currently increasing its energy to 14 TeV, but we will have to wait a year or two to find what it reveals about physics at that energy.

At this writing, we now have both the data and a theory that describes the available data to inform us, with confidence, of the physics of the universe when its temperature was 1 TeV (10¹⁶ degrees), which occurred when it was only 10^–12 second (one trillionth of a second) old.

PARTICLES OR FIELDS?

Relativity and quantum mechanics, and their offspring, quantum field theory and the standard model, compose the set of the most successful scientific theories of all time. They agree with all empirical data, in many cases to incredible precision. Yet if you follow the popular scientific media, you will get the impression that there is some giant crisis with these theories because no one has been able to satisfactorily explain what they “really mean.”

Charlatans have exploited this perception of crisis, convincing large numbers of unsophisticated laypeople that the “new reality” of modern physics has deconstructed the old materialist, reductionist picture of the world. In its place we now perceive a holistic reality in which the fundamental stuff of the universe is mind—a universal cosmic consciousness. I call this quantum mysticism.17

Unfortunately, some theoretical physicists have unwittingly encouraged this new metaphysics by conjuring up their own mystical notion of reality. David Tong presents a typical example in the December 2012 Scientific American, writing,

Physicists routinely teach that the building blocks of nature are discrete particles such as the electron or quark. That is a lie. The building blocks of our theories are not particles but fields: continuous, fluidlike objects spread throughout space.¹⁸

This is highly misleading. No one has ever observed a quantum field. However, we observe what can always simply and accurately be described as pointlike particles.

Quantum fields are purely abstract, mathematical constructs within quantum field theory. In the theory, every quantum field has associated with it a particle that is called the “quantum of the field.” The photon is the quantum of the electromagnetic field. The electron is the quantum of the Dirac field. The Higgs boson is the quantum of the Higgs field. In other words, like love and marriage, you can't have one without the other. The building blocks of our theories are fields and particles.

But note that what Tong calls “a lie” is the notion that the building blocks of nature are discrete particles while it is fields that are the true building blocks of our theories. That is, he is equating ultimate reality to the mathematical abstractions of the currently most fashionable theory. That means it will change when the fashions change.

Tong is revealing his adoption of a common conception that exists among today's theoretical physicists. They believe that the symbols that appear in their mathematical equations represent true reality while our observations, which always look like localized particles, are just the way in which that reality manifests itself. In short, they are Platonists. It is important to note that twentieth-century greats Paul Dirac and Richard Feynman were not part of that school. And not all contemporary theorists are “field Platonists.”

In his 2011 book Hidden Reality, physicist and bestselling author Brian Greene has this to say about particles and reality:

I believe that a physical system is completely determined by the arrangement of its particles. Tell me how the particles making up the earth, the sun, the galaxy, and everything else are arranged, and you've fully articulated reality. The reductionist view is common among physicists, but there are certainly people who think otherwise.19

No one claims that the particles of the standard model must be thought of as classical billiard balls. But as philosopher Meinhard Kuhlmann points out, quantum fields also should not be thought of as classical fields such as the density of a gas. He writes:

How can there be so much fundamental controversy about a theory that is as empirically successful as quantum field theory? The answer is straightforward. Although the theory tells us what we can measure, it speaks in riddles when it comes to the nature of whatever entities give rise to our observations. The theory accounts for our observations in terms of quarks, muons, photons and sundry quantum fields, but it does not tell us what a photon [field] or a quantum field really is. And it does not need to, because theories of physics can be empirically valid largely without settling such metaphysical questions.20

Although he does not claim this view for himself and presents all the alternatives, pro and con, Kuhlmann describes common positions found among hard-nosed experimentalists:

For many physicists, that is enough. They adopt a so-called instrumentalist attitude: they deny that scientific theories are meant to represent the world in the first place. For them, theories are only instruments for making experimental predictions.

While others are a bit more flexible,

Still, most scientists have the strong intuition that their theories do depict at least some aspects of nature as it is before we make a measurement. After all, why else do science, if not to understand the world?

I would just add that if some theory does not at least in principle imply some observable effect, it cannot be tested and we have little reason to think it correctly models reality. While such a theory may be mathematically or philosophically interesting, its elements are not very good candidates for “aspects of nature.”

While I cannot prove that particles are elements of ultimate reality, at least what we observe when we do experiments look a lot more like localized particles and are far simpler to comprehend than otherworldly quantum fields. After all, astronomical bodies look like particles when viewed from far enough away and we don't question their reality. So, for all practical purposes we can think of particles as real until we are told otherwise by the data.

Furthermore, as we saw in chapter 6, the wavelike phenomena that are associated with particles in quantum mechanics, and quantum field theory, are not properties of individual particles but of ensembles of particles. The expression “wave-particle duality” does not accurately describe observations. A lone particle is never a wave.

We also often hear that quantum mechanics has destroyed reductionism and replaced it with a new “holistic” worldview in which everything is connected to everything else. This is not true. Physicists, and indeed all scientists and, notably, physicians, continue to break the matter up into parts that can be studied independently. After a brief dalliance with holism in the 1960s, the success of the standard model returned physicists to the reductionist method that has served them so well throughout history of science, from Thales and Democritus to the present.

THE BIRTH OF PARTICLE ASTROPHYSICS

As we saw in chapter 10, by the 1990s nuclear astrophysicists had successfully described the formation of light nuclei when the universe was one second old by applying the model of big-bang nucleosynthesis. The calculated abundances agreed precisely with the data, including the very sensitive relationship between deuteron abundance and baryon density. Anyone seeing this result has to come away convinced that the big bang really happened.

While this was going on, particle astrophysicists (in most cases, the same people, with David Schramm leading the way) were applying the new standard model of elementary particles to describe what may have happened prior to 1 second. They adopted the idea of symmetry breaking, which had become fundamental in physics, to characterize a series of phase transitions starting from the first definable moment. At each critical temperature, the universe changed phase—like water freezing to ice—from higher symmetry to lower symmetry, with different sets of particles and forces emerging as described by the new symmetry.

Recall that prior to 1 second, when the temperature was above 1 MeV, the universe was a quasi-equilibrium mixture of electrons, neutrinos, antineutrinos, and photons in roughly equal numbers, along with a billion times fewer protons and neutrons that would form the light nuclei as the universe cooled and their equilibrium could no longer be maintained.

Let us now go back farther in time to 10^–6 second, when the temperature was 1 GeV. This was still an era that we can describe with known physics, empirically as well as theoretically, so we are not just speculating. Just prior to this time, the universe was composed of the elementary particles listed in table 11.1 and there were no protons, neutrons, or composite hadrons of any type. The quarks were not free, however (they never are in quantum chromodynamics), but were confined along with gluons to a soup pervading the universe called a quark-gluon plasma. When the temperature dropped to around 1 GeV, a spontaneous phase transition occurred that generated the color-neutral hadrons my colleagues and I were studying in the 1960s with particle accelerators. Few hadrons except the protons and neutrons hung around in the early universe, however, because of their short lifetimes.

Although our physics measurements have so far extended to around 1 TeV, below which the strong, weak, and electromagnetic forces are distinct, the standard model makes the underlying assumption that the weak and electromagnetic forces were unified above that energy, prior to a trillionth of a second after the start of the big bang. The LHC allows us, for the first time, to empirically probe the region of higher symmetry and provide data on the physics of the universe earlier than 10^–12 second.

MATTER-ANTIMATTER ASYMMETRY

Despite its success, the standard model does not explain a pretty important feature of our universe: the preponderance of matter over antimatter.

One of the principles contained in the standard model is baryon-number conservation. Each baryon has a baryon number B = +1; antibaryons have B = –1. Quarks have B = +1/3, antiquarks have B = –1/3. Leptons, gauge bosons (that is, the force mediators), and Higgs boson have zero baryon number. Baryon-number conservation says that the total baryon number of the particles engaged in an interaction is the same after the reaction has taken place as before. No reaction in particle physics, nuclear physics, and chemistry has ever been found that violates this rule.

If we reasonably assume that when the universe came into being its total baryon number was zero, then it should have equal numbers of baryons and antibaryons. By now they would have totally annihilated with one another and there wouldn't be any protons and neutrons to make atomic nuclei.

The standard model also contains a principle of lepton-number conservation. Leptons have L = +1, antileptons have L = –1. Baryons and gauge bosons have zero lepton number. So, by the same token, all the charged leptons and antileptons would have annihilated and there wouldn't be any electrons left. In short, the standard model says that the universe should be nothing but photons and neutrinos. This means no atoms, no chemistry, no biology, no you, me, or the family cat.

However, here we are. Protons and electrons outnumber antiprotons and positrons by a factor of a billion to one. At some point very early in the universe, before nuclei and atoms were formed, baryon-number conservation and lepton-number conservation were violated and the large asymmetry between matter and antimatter was generated.

If baryon-number conservation is violated, then protons must be ultimately unstable. We need not worry about electrons being unstable, because they are so light there are no lighter charged particles they can decay into; charge conservation prevents them from decaying into photons and neutrinos. By contrast, there are many charged leptons that protons can decay into. The particle data tables, which list all the properties of elementary particles, provide dozens of possible decay modes.21 Here's just one example:

p → e⁺ + γ

where e⁺ is the positron. Note violation of lepton-number as well as baryon-number conservation.

Even before the standard model was completed in the 1970s, theorists were looking for ways it could be extended. One class of models considered was called GUTs, for grand unified theories. The standard model had unified the electromagnetic and weak forces into a single electroweak force, but the strong force was independent. GUTs attempted to unify the strong force with the others.

Most GUTs provided for baryogenesis, the generation of baryon asymmetry, along with leptogenesis, the generation of lepton asymmetry. A possible mechanism based on the original suggestion made in 1967 by the famous Russian physicist and political dissident Andrei Sakharov²² is shown in figure 11.4. It involves a new gauge boson called X and its antiparticle.

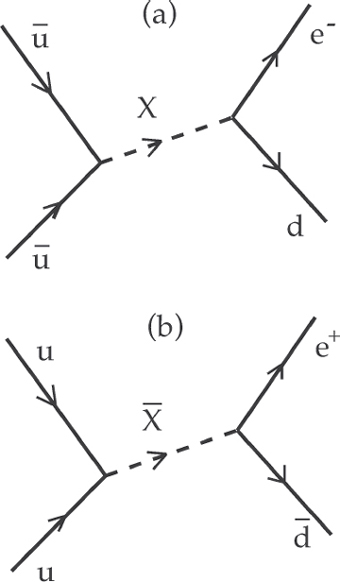
Figure 11.4. A mechanism for B and L violation. In figure 11.4 (a) two antiquarks annihilate into an X boson producing a quark and electron for a net gain of one unit each in baryon and lepton numbers. In (b) the same reaction is shown with particles replaced by their antiparticles, with the corresponding decrease in B and L by one unit each. CP-violation results in a greater rate for (a) than (b), generating a baryon and lepton excess. Image by the author.

The simplest of the early GUTs was proposed by Howard Georgi and Sheldon Glashow in 1974.23 I will call it GG-GUT. (Technically it was called minimal SU(5).) It had the virtue of enabling a prediction of 10³² years for the proton lifetime.²⁴

THE SEARCH FOR PROTON DECAY

This predicted proton-decay lifetime from GG-GUT was well within the range of existing technology, and four experiments were quickly mounted to seek proton decay. These experiments were conducted deep underground in mines in order to reduce background radiation, especially from high-energy cosmic-ray muons that can penetrate deep into the earth. At least two of the experiments were fully capable of seeing proton decay if the lifetime was 10³² years or less. One was in a salt mine near Cleveland, called IMB for the three primary institutions involved (University of California–Irvine, University of Michigan, and Brookhaven National Laboratory). Colleagues of mine at the University of Hawaii were also involved. The other sensitive experiment was in a zinc mine in Kamioka, Japan, and called KAMIOKANDE (Kamioka Nucleon Decay Experiment).

By 1982, all four experiments reported seeing no decays at the GG-GUT expected rate, thereby falsifying the model. (Despite some philosophers’ assertions otherwise, falsification does happen in science.) Unfortunately, none of the other proposed GUTs predicted measurable proton lifetimes or other viable empirical tests.

Experiments continued to improve, with the most sensitive being an upgraded experiment in Kamioka called Super-Kamiokande. I played a small role in Super-K before retiring from research in 2000. Super-K has provided the best lower limit on proton decay so far, 1.01 × 10³⁴ years as of 2011, two orders of magnitude higher than the GG-GUT prediction.²⁵

Sometimes negative results are as important as positive ones. Knowing the lower limits for proton-decay lifetimes in various decay channels provides invaluable input for theorists as they look for physics beyond the standard model. They can rule out models that predict violations of that limit. When and if proton decay is observed, the rates by which it decays into various channels will help determine the structure of the physics beyond the standard model.

The underground experiments also had some positive ancillary discoveries that were almost as significant as the failure to see proton decay. In 1987, the experiments in Cleveland and Kamioka detected neutrinos from the supernova SN 1987A in the Large Magellanic Cloud, as mentioned in chapter 10.²⁶ This was the first observation of neutrinos from outside the solar system.

THE GUT PHASE TRANSITION

Given the success of the standard model, we can reasonably assume that prior to the electroweak phase transition at a presently estimated 173 GeV in temperature, which occurred at about 10^–11 second, the universe can be described by the standard model with electroweak unification. That is, the strong force is still distinct but electromagnetism and the weak force are unified. The universe at this time still consisted of the quarks, leptons, and gauge bosons in table 11.1, but they were all massless and there were no Higgs bosons. Particles still outnumbered antiparticles by a billion to one. At some higher energy and earlier time, there almost certainly had to be a phase transition from a state of higher symmetry that, itself, was the result of a phase transition from an even higher symmetric state.

The best candidate remains some kind of GUT in which the strong and electroweak forces are united and both baryon- and lepton-number conservation are violated. This GUT, in turn, arose from another symmetry at higher energy in which B and L were conserved.

Most GUTs that have been proposed exhibit these properties. Here the symmetry is manifested by no distinction being made between quarks and leptons so that reactions such as those shown in figure 11.4 can take place. The X particle that is exchanged in the figure can be thought of as a “leptoquark,” a combination of quark and lepton. The breaking of B and L come about, according to Sakharov, by differences in reaction rates caused by CP violation.

In the more symmetric state prior to the GUT phase transition, CP is invariant and B and L conservation are each restored. So the universe starts out with all the symmetries and equal numbers of particles and antiparticles. The asymmetry of matter and antimatter is generated after the phase transition from this earlier state to the GUT state.

So all we have to do is keep building more and more powerful colliding-beam accelerators so that we can keep probing farther and farther back in time until we reach the GUT regime. The trouble is, we aren't even close to having enough energy. The GUT phase transition is estimated to occur at about 10²⁵ eV, twelve orders of magnitude above the energy of the LHC. A vast “desert” may exist between the GUT and electroweak phase transitions, during which time the universe remains in the unbroken phase of the electroweak-unified state.

At least the LHC will enable us to explore the unbroken phase. But will we ever be able to probe beyond this state? It is highly unlikely with accelerators, at least in any foreseeable future. However, we do have another window on the very early universe, and that is proton decay. Super-K may be nearing the point where proton decay is observed. Several GUTs predict decay modes that are within the range of Super-K or a larger detector.

SUPERSYMMETRY (SUSY)

A promising approach to physics beyond the standard model that has attracted the attention of a generation of theoretical particle physicists is supersymmetry, referred to as SUSY. This is a symmetry principle in which physical models do not distinguish between fermions and bosons. Recall that fermions have half-integer spins while bosons have integer or zero spins.

Under SUSY, every elementary particle is accompanied by a sparticle of the opposite spin property. Thus the spin-1/2 electron is accompanied by a spin-zero selectron, the spin-1 photon by a photino of spin 1/2, the spin-1/2 quark by a spin-zero squark.

If SUSY were a perfect symmetry, the sparticles would have the same masses as their partners and not only would we see them but they would not obey rules such as the Pauli exclusion principle that distinguishes bosons from fermions. In that case, there would be no chemistry. Since no sparticle has yet been seen and we have chemistry, the symmetry is broken at the low energies (low compared to those in the early universe) where we are able to live. If sparticles exist, they must have very high masses.

As we will see in chapter 13, the Large Hadron Collider has so far failed to detect any of the expected sparticles, leaving the whole notion in grave doubt.

M-THEORY

Supersymmetry offered the possibility of finding a theory that unified gravity with the other forces of nature described in this chapter, what is often referred to as the theory of everything (TOE). Originally called string theory, it was conjectured that the universe has more than three dimensions of space, with these extra dimensions curled up so tightly that that are undetectable. String Theory replaced zero-dimensional particles with one-dimensional strings.

Eventually a further generalization was introduced called M-theory in which objects of higher dimension were included, called branes. A two-dimension brane is called a membrane. A p-dimensional brane is called, appropriately enough, a p-brane. A particle is a 0-brane, a string a 1-brane, and a membrane a 2-brane. M-theory allows up to p = 9.27 Although M-theorists have made many significant mathematical discoveries in their quest for the theory of everything, they have not yet managed to come up with empirical prediction that can be tested by experiment. Furthermore, since as just mentioned, supersymmetry has not yet been confirmed, as it was expected to be at the LHC. Although it gets a lot of publicity, leading the layperson to think the TOE is just around the corner, M-theory remains far from being verified and may soon be falsified.