Many firefighter exams include mathematical problems pertaining to the job of firefighting. Knowledge of basic arithmetic, algebra, and geometry is necessary in the fire service. Measuring gas/oil mixtures that fuel portable power saws, mixing cleaning fluids with water during maintenance chores, determining the placement of a ladder for proper climbing angle, and monitoring gallons per minute (GPM) flowing through hose lines are just a few examples of how firefighters use numbers. The mathematics selected for this review cover the most common areas included in previous firefighter examinations, basic terminology, symbols, and order of operations.
There are many terms used in mathematics that you should understand. A list of some of the more common terms and their definitions follows:
Real numbers—both rational and irrational numbers
Whole numbers—the counting numbers that include zero
Example: 0, 1, 2, 3, . . .
Natural (positive) numbers—all whole (counting) numbers greater than zero
Example: 1, 2, 3, 4, …
Negative numbers—all numbers less than zero
Example: –1, –2, –3, . . .
Integers—all positive and negative whole numbers, including zero, but not including fractions and decimals
Example: . . . –2, –1, 0, 1, 2, . . .
Fraction—part of a whole number
Example: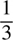 
Mixed number—a whole number and a fraction
Example: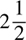 
Rational numbers—all numbers that can be expressed as the ratio of two integers (fractions and integers)
Example: x/y where x and y are integers
Irrational numbers—all numbers that cannot be expressed as the ratio of two integers
Example: π (3.14 . . .) and many square roots 
, etc.
Term—a single number or the product of one or more numerical (number) coefficient and/or literal (letter) coefficient factors. Like terms have the same literal factor. Unlike terms do not have a common literal factor.
Example: (like terms) 2a and 3a
Example: (unlike terms) 6, 3x, and yz
Factor—an individual number (numerical) or letter (literal) in a term
Example: 2, a, and b are factors of the term 2ab
Algebraic expression—two or more terms connected by plus or minus signs
Example: 4k + 7
Algebraic equation—a statement representing two things that are equal to one another
Example: 12x – 8x = 4x
Many numerical expressions include two or more operations—for example, exponents, division, and addition. These operations must be performed in the correct sequential order. The acronym PEMDAS helps in remembering what the correct sequence is.
PEMDAS—Please Excuse (My Dear) (Aunt Sally)—stands for Parenthesis, Exponents, Multiplication/Division, then Addition/Subtraction.
When there are two or more parentheses, grouping symbols, perform the innermost grouping symbol first. Exponents should be worked on next. Multiplication and division, as well as addition and subtraction, are grouped to denote that when these operations are next to each other, just perform the math from left to right.
PEMDAS is used when evaluating formulas, solving equations, solving algebraic expressions, and working with monomials and polynomials.
Example: 2 + 4[3 + (4 – 2)2]
2 + 4[3 + (2)2]
2 + 4[3 + 4]
2 + 4[7]
2 + 28
30
Example: 2 + 3(6 + 1)2
2 + 3(7)2
2 + 3(49)
2 + 147
149
Odd numbers are whole numbers that when divided by 2 leave a remainder.
Example: –3, –1, 1, 3, . . . (3 ÷ 2 = 1 with 1 remainder)
Even numbers are whole numbers that when divided by 2 leave no remainder. Zero is included.
Example: –4, –2, 0, 2, 4, . . . (4 ÷ 2 = 2)
Note: Division by zero is undefined and therefore has no meaning regardless of whether the dividend is odd or even.
Negative and positive numbers are signed numbers. A thermometer has a scale having both positive and negative numbers. The numbers run along a vertical number scale with positive numbers, indicated by the (+) sign, being above zero and negative numbers, indicated by the (–) sign, found below zero.
The absolute value of a number is its value when the sign is not taken into consideration. The symbol for absolute value is | |.
Example: |7| = 7 and |–7| = 7
Adding a negative number is the equivalent of subtracting a positive number.
Example: 8 + (–4) = 4 is equivalent to 8 – 4 = 4
Conversely, adding a positive number to a negative number is the same as subtracting the negative number.
Example: –4 + (+8) = 4 is equivalent to 8 – 4 = 4
To add two negative numbers (like signs), add their absolute values and prefix the sum with their common sign.
Example: –6 + (–9) = –(|6| + |9|) = –15
Subtracting a negative number from a positive number is the equivalent of adding a positive number.
Example: 8 – (–4) = 12 is equivalent to 8 + 4 = 12
Conversely, subtracting a positive number from a negative number is the equivalent of adding the absolute value of two negative numbers and prefixing the answer with a minus sign.
Example: –4 – (+2) = –6 is equivalent to –(|–4| + |+2|) = –(4 + 2) = –6
When multiplying or dividing two signed numbers, the product (multiplication) or quotient (division) will be positive if the signs are the same. If the signs are different, however, the product or quotient will be negative.
Example: (–5) × (–7) = +35
Example: (–6) ÷ (–3) = +2
Example: (–5) × (7) = –35
Example: (–6) ÷ (3) = –2
Example: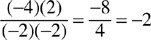 
When multiplying more than two numbers, the product is always a negative number if there are an odd number of negative factors. Conversely, if there is an even number of negative factors, the product is always a positive number.
Example: (2)(4)(–4) = –32
Example: (8)(2)(–3)(–4) = 192
The product of two or more numbers is always zero if any of the numbers is zero.
Example: (–9)(–3)(0) = 0
When multiplying numbers in exponential form (a number being multiplied by itself), odd exponents (powers) of negative numbers result in a product that is negative, and even exponents of negative numbers have positive products.
Example: (–3)3 (to the third power) = –3 × –3 × –3 = –27
Example: (–6)2 (to the second power) = –6 × –6 = 36
Note: Division by zero is undefined and therefore has no meaning regardless of whether the dividend (numerator) is a positive or negative number.
Unique numbers whose sole factors are 1 and themselves are called prime numbers. All prime numbers except 2 are odd.
Example: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, . . .
To calculate the prime factorization of a number, divide it and all its factors until every remaining integer of the group is a prime number.
Example: 24 = 2 × 12 = 2 × 2 × 6 = 2 × 2 × 2 × 3. The numbers 2 and 3 are both prime numbers.
Example: 12 = 2 × 6 = 2 × 2 × 3. The numbers 2 and 3 are both prime numbers.
To find the greatest common factor (GCF) of the two examples above, determine the intersection of prime numbers of the two prime factorizations. Because both prime factorizations contain (2 × 2 × 3), the GCF is 12.
Multiples of a number are its products with the natural numbers.
Example: 4 × 1 = 4, 4 × 2 = 8, 4 × 3 = 12, 4 × 4 = 16
The multiples of 4 are therefore 4, 8, 12, 16, and so on.
The least common multiple (LCM) is also found using prime factorization. The LCM is equal to the multiplication of each factor by the maximum number of times it appears in either number. Using the two prime factorization examples above, once again, the number 2 appears three times for the number 24 and two times for the number 12, and the number 3 appears one time for both 24 and 12. Therefore, the LCM of 24 and 12 is the product of 2 × 2 × 2 × 3 = 24.
A fraction is a part of a whole number and consists of two expressions, an upper number (numerator) and a lower number (denominator), which are called the terms of the fraction. The fraction represents a division process whereby the numerator is divided by the denominator.
Example: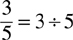 
A fraction with a smaller numerator than denominator is a proper fraction.
Example: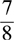 
A fraction with a larger numerator than denominator is an improper fraction.
Example: 
To determine if two fractions are equivalent (equal), multiply the numerator and denominator of one fraction by the same number so that the denominators of the fractions are equal.
Example: Determine if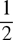 
is equivalent to 
.
To have the denominators of both fractions the same—in this case, 8—you need to multiply the denominator of the first fraction by 4 and multiply the numerator by the same number, 4. Multiplying the numerator and denominator of the first fraction by 4 gives the second fraction. Therefore, the two fractions are equivalent.
Example: 
Example: Determine if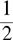 
and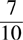 
are equivalent.
To have the denominators of both fractions the same, you need to multiply the denominator of the first fraction by 5. Then, multiply the numerator by the same number, 5.
Example: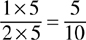 
The result,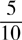 
is not the same as 
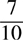, so the two fractions—
and 
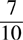—are not equivalent.
Note: If you multiply or divide both the numerator and the denominator of a fraction by the same number (excluding zero), you will not change the value of the fraction. Remember, if the numerator and denominator of a fraction are both the same number, the fraction is equal to 1, so multiplying the numerator and denominator by the same number is the same as multiplying the fraction by 1.
To reduce a fraction to its lowest form, divide the numerator and the denominator by their greatest common factor (GFC). The GCF of two numbers is the largest factor that is common to both.
Example: Reduce 
to its lowest form.
Prime factorization of 25 = 5 × 5
Prime factorization of 60 = 2 × 30 = 2 × 5 × 6 = 2 × 5 × 2 × 3 = 2 × 2 × 3 × 5
GCF of 25 and 60 = 5
Divide the numerator and denominator by the GCF, 5, to reduce the fraction.
The fraction 
is at its lowest form since there is no number except 1 that can divide both 5 and 12.
If the denominators of two fractions are equal, then the fraction with the larger numerator is bigger. If the numerators of the two fractions are equal, then the fraction with the smaller denominator is bigger.
When comparing fractions that have different numerators and denominators, cross multiply the numerator of each fraction by the denominator of the other fraction. Write the product of each multiplication next to the numerator you used to get it. Compare the products on each side of the fractions to determine which of the two fractions is greater.
Example: Compare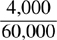 
and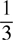 
.
Cross multiply:
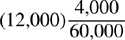and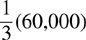 
12,000 is less than 60,000
therefore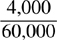 
is less than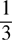 
Fractions having the same denominators require only the adding or subtracting of the numerators.
Example: 
Example: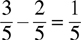 
Fractions having different denominators require first finding a common denominator or least common denominator (LCD) before you can either add or subtract them.
Example: 
The least common multiple of 5 and 3 is 15; therefore the LCD is 15.
Multiply the numerator and denominator of the first fraction by the number required to change the denominator to 15—in this case, 3.
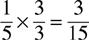
Repeat the process for the second fraction by multiplying the numerator and denominator by 5 (the number required to change the denominator to 15).
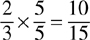
Then add the numerators and place the sum over the common denominator:
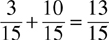
Note: Multiplying the denominators together to get a common denominator allows you to omit having to find the LCD, and sometimes will, in fact, give you the least common denominator. However, there are two drawbacks to this approach: first, you may be working with larger numbers since you may not be using the least common denominator; and second, you will have to reduce your answer to the lowest form of the fraction.
To multiply fractions, multiply their numerators and denominators.
Example: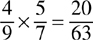 
To divide fractions, simply invert the second fraction and multiply the numerators and denominators. Remember: multiplication and division are inverse operations (as are addition and subtraction).
Example: 
A mixed number consists of an integer and a fraction. Mixed numbers must be converted into fractions prior to performing addition, subtraction, multiplication, and division operations. To convert a mixed number to a fraction, multiply the integer of the mixed number by the denominator of the fraction and then add the product to the numerator of the fraction and put that number over the denominator of the original fraction.
Example: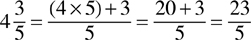 
Numbers that contain a decimal point are called decimals. The number to the left of the decimal point is a whole number, and the number to the right of the decimal point is called the tenths digit. The tenths digit gives you the number of tenths that are added to the whole number. If there are two numbers to the right of the decimal point, then both numbers to the right are the number of hundredths to be added to the whole number. Three numbers to the right of the decimal point would indicate that all three numbers to the right are the number of thousandths to be added to the whole number, and so forth.
Decimals, indicating parts of a whole number, can be converted into fractions and vice versa.
Example: Convert 0.4 to a fraction
Count the number of decimal places—in this case, tenths. Use 10 as the denominator of the fraction and place the decimal digits without the decimal point as the numerator. The fraction is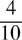 
. Reduce it to 
.
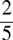Example: Convert 2.3 into a mixed number.
Count the number of decimal places and use that number to find whether the denominator should be tenths, hundredths, or thousandths as explained above. If the decimal number is greater than 1, keep the whole number and write the decimal digits without the decimal points as a numerator. Therefore,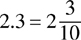 
.
To convert a proper fraction into a decimal, divide the numerator by the denominator to obtain the decimal equivalent.
Example: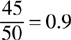 
To convert an improper fraction into a decimal, first convert the improper fraction into a mixed number; keep the whole number and divide the remainder (the numerator by the denominator).
Example: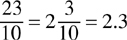 
Reducing a decimal to fewer decimal places is known as rounding off. If the digit in the decimal place to be eliminated is 5 or greater, increase the digit in the next decimal place to the left by 1. If the digit to be eliminated is less than 5, leave the retained digits unchanged.
Examples: 0.2344 rounded to the nearest thousandth is 0.234
3.14 rounded to the nearest tenth is 3.1
When adding and subtracting decimals, write the numerals one above the other with their decimal points lined up.
Examples:
When multiplying two decimals, initially ignore the decimal points and simply multiply the two numbers to get the product. Then, add together the number of digits to the right of the decimal point in each number and put the decimal in the product so that there is the same number of decimal places as in the numbers multiplied.
Example:
Count one digit to the right of the decimal point in 1.3 plus one digit to the right of the decimal point in 2.2 and place the decimal point so that there are two digits to the right of the decimal point in the product.
To divide one decimal into another, move the decimal in the divisor to the right until it is a whole number and then move the decimal to the right the same number of places in the dividend.
Example: 4.5 ÷ 1.5
= 45 ÷ 15
= 3
A percent is defined as one part in a hundred. The whole amount can be defined as 100 percent (%) and can be divided into 100 equal portions.
To convert a decimal to a percent, move the decimal point two places to the right and insert the % sign at the end of your answer.
Example: 0.567 = 56.7%
To convert a percent to a decimal, move the decimal point two places to the left and remove the % sign at the end of your answer.
Example: 56.7% = 0.567
To convert a fraction to a percent, multiply the fraction by 100%. You can express 100% as a fraction by placing it over 1.
Example: Convert 
to a percent.
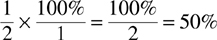
To convert a percent to a fraction, remember that the definition of percent is one part in a hundred. Remove the % sign and multiply the percent value by 1/100 and then reduce the fraction to its lowest terms.
Example: Convert 40% to a fraction.
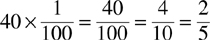
To convert a mixed number percent to a fraction, eliminate the % sign and convert the mixed number to an improper fraction. Then multiply the improper fraction by 1/100 to obtain the fraction.
Example: Convert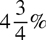 
to a fraction.
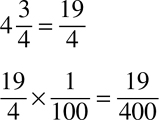
To find the part when given the whole and the percent, use the formula:
Part = % · Whole ÷ 100
Example: What is 54% of 50?
Part = % · Whole ÷ 100
Part = (54)(50) ÷ 100
Part = 2,700 ÷ 100 = 27
To find the % when given the whole and the part, use the formula:
% = Part ÷ Whole · 100
Example: What percent of 60 is 12?
% = 12 ÷ 60 · 100
% = 0.2 · 100
% = 20
To find the whole when given the part and %, use the formula:
Whole = Part ÷ % · 100
Example: 6 is 15% of what number?
Whole = Part ÷ % · 100
Whole = (6) ÷ (15) · 100
Whole = 0.4 · 100 = 40
Example: What is 60 increased by 10%?
Part = % · Whole ÷ 100
Part = (10)(60) ÷ 100
Part = 600 ÷ 100 = 6
Add the percentage increase to the original number.
60 + 6 = 66
Example: What is 12 decreased by 25%?
Part = % · Whole ÷ 100
Part = (25)(12) ÷ 100
Part = 300 ÷ 100 = 3
Subtract the percentage decrease from the original.
12 – 3 = 9
A ratio is a comparison of two numbers or objects. The symbol : is used to separate the values in the ratio. To compare ratios, convert them to fractions by placing the number to the left of the symbol used to separate the two numbers as the numerator and the number to the right of the symbol as the denominator. The order of values in the given expression is important when notating the ratio.
Example: In a group of 30, there are 24 men and 6 women. The ratio of men to women is 24:6 or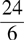 
.
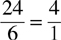
Therefore, the expressed ratio of men to women can be simplified to 4:1 (for every 4 men in the group, there is 1 woman).
Equivalent (equal) ratios have the same proportion when both sides of the ratio are multiplied or divided by the same number.
Example: 1:6 and 5:30 and 20:120 are all equivalent ratios, but 1:6 is the simplest form.
A proportion is an equation of two ratios that are equal to each other. A basic property of a proportion is that the product of the means is equal to the product of the extremes.
Example: a/b = c/d or ad = bc (b and c are the means and a and d the extremes)
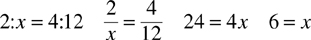
Note: Two quantities are in direct proportion when they decrease or increase by the same factor.
Probability attempts to quantify the notion of probable. The probability of an event occurring, P(E), is generally represented as a real number between 0 and 1. The more likely the probability of an event occurring, the closer the probability is to 1. It should be understood, however, that a probability of 0 is not impossible, nor a probability of 1 a certainty.
Note: If P(E) is the probability that an event will occur, then P(E) cannot be a negative number.
Example: A coin is thrown in the air five times. If the coin lands with the tail up on the first four tosses, what is the probability that the coin will land with the tail up on the fifth toss?
Answer: The fifth toss is independent of the first four tosses, and therefore the probability remains one out of two.
For any word problem that involves two or more actions or objects, each having a number of choices, and asks for the number of combinations, use the counting principle formula:
Number of ways = x ∙ y
Example: A firefighter, during her meal period, wants a sandwich and a seltzer from the corner delicatessen. If the deli has six choices of sandwiches and four choices of seltzer to choose from, how many different ways can she order her lunch?
Number of ways = (6 sandwiches)(4 seltzers)
Number of ways = 24
Example: How many different five-letter arrangements can be formed using the letters FIRES, if each letter is used only once?
Five letters can be used to fill the first position in the new word, then four letters to fill the second position, three for the third position, and so on. Therefore, the number of ways is: 5 × 4 × 3 × 2 × 1 = 120.
An ordered list of terms in which the difference between consecutive terms is constant is called an arithmetic sequence. If you subtract any two consecutive terms of the sequence you will obtain the same difference, known as the constant interval between the terms.
Example: 2, 5, 8, 11, 14, 17, 20, . . .
20 – 17 = 3; 17 – 14 = 3; 5 – 2 = 3
The exponent in an expression such as 32 shows how many times the base—in this case, 3—is multiplied by itself to find the result, known as the power.
Examples: 32 = 3 × 3 = 9; 9 is the second power of 3
63 = 6 × 6 × 6 = 216; 216 is the third power of 6
Any base raised to the power of zero is equal to 1.
Examples: 60 = 1; 40 = 1
Any base raised to the power of 1 is equal to itself.
Example: 71 = 7; –551 = –55
A negative base number raised to an even exponent will be positive, while a negative base number raised to an odd exponent will be negative.
Examples: (–3)2 = 9; (–3)3 = –27
Any base raised to a negative power is equal to the reciprocal of the base number (a fraction with 1 placed over the number) raised to the opposite power.
Example: 
When multiplying two like bases, each with a positive integer exponent, add the exponents.
Example: (42) × (43) = 4(2 + 3) = 45 = 1,024
To verify this: (42 = 16) × (43 = 64) = 16 × 64 = 1,024
When multiplying a base with two exponents, multiply the exponents.
Example: (23)4 = 2(3 × 4) = 212 = 4,096
When dividing two like bases, each with an exponent, subtract the exponents.
Example: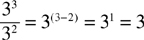 
To verify this: (33 = 27) ÷ (32 = 9) = 27 ÷ 9 = 3
Roots and exponents (powers) are reciprocal. The principal square root of a nonnegative real number is denoted by the symbol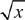 
where x represents the nonnegative real number (x is greater than zero) whose square (the result of multiplying the number by itself) is x. The symbol 
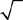is called the radical sign and the number under the radical sign is called the radicand.
Examples: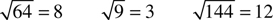 
The first 10 square numbers and their roots are listed below.
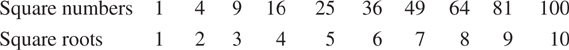
A statement that one expression is greater than or less than another expression is called an inequality.
Several symbols are used in statements and word problems involving inequalities. A list of these symbols and their meaning follows:
< a < b; a is less than b (point is always toward the lesser expression)
> b > a; b is greater than a
≤ less than or equal to
≥ greater than or equal to
≠ not equal to
The origins of algebra can be traced to the ancient Egyptians and Babylonians who used an early type of algebra more than 3,000 years ago. This section reviews the fundamentals of algebra and its application in solving word problems asked in previous firefighter exams.
When a number’s value is unknown, a symbol (such as a, b, x, or y), called a variable, is used to represent it.
Example: 5x + x = 5x + 1x = 6x
Note: If no number appears in front of the variable, the number (coefficient) is 1.
Variables can be canceled in fractions the same way whole numbers are, but only factors, not terms, can be canceled.
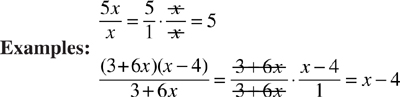
In the example above, 3 + 6x is a factor of (3 + 6x)(x – 4) and therefore can be canceled.
When working with an equation dealing with a negative variable (–x), you must change the equation in terms of (x) using multiplication or division.
Example: – x = 5 Multiply both sides of the equation by –1
(–1) (–x) = 5 (–1)
x = –5
Note: If the term containing the variable in the algebraic equation has a negative coefficient (factors being multiplied), multiply both sides of the equation by the reciprocal (inversion) of the coefficient, which will also be negative.
Example: –2x = 8
Multiply both sides by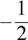 
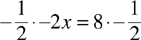
x = –4
When adding and subtracting fractions with variables, treat the variables as if they were prime numbers (to find the LCD).
Example: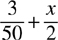 
. The least common denominator is 50.
Multiply fractions with variables the same way you would multiply fractions without variables. Multiply the numerators first and then multiply the denominators.
Examples: 
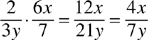
Dividing fractions with variables is similar to dividing fractions without variables. Invert the second fraction and multiply the fractions.
Example: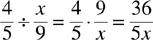 
A monomial is a single term that has no plus or minus sign between entries. Examples of monomials are 3x; – 22y2; – 3xy2; 380xy2. But 4x + 2 and are not monomials because they have a plus or minus sign between entries.
A polynomial is two or more monomials attached with plus signs and/or minus signs.
Examples: 4x + 2; 4y – 3; 2x2 + 3x; 7x2 – 9x + 1
Expressing an algebraic expression as a product of certain factors is called factoring. It generally involves finding one factor of a product and using it as a divisor to find other factors. Factoring is important in algebra and useful in simplifying expressions and solving equations.
FOIL is a method of multiplying terms and subsequently adding or subtracting like terms to get a polynomial result.
Example: (x + 5) (3x – 7)
Example: (4x – 8) (2x + 6)
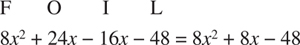
Note: The distributive laws allow us to execute the often easier task of completing two smaller multiplications and calculating the sum, rather than performing one multiplication involving large numbers.
The following sections show applications of arithmetic and algebraic equations.
Example: George rents a car for a day from a company charging $60 a day, plus a lateness fee of $10 an hour for cars not brought back on time. If George returns the car the next day two hours late, how much would he be obligated to pay the rental company?
Answer: $60 for the day, plus $20 for two-hour late fee = $80.
Example: A beachcomber collects $43.20 off the sand on Saturday and $27.67 on Sunday. How much more money did the searcher collect on Saturday compared to Sunday?
Answer: $43.20 – $27.67 = $15.53.
Example: An EMT checks the pulse of a rescued fire victim. The victim’s pulse count is 19 for the 15 seconds that the pulse was examined. What is the number of beats per minute?
Answer: Since 15 seconds is ¼ of a minute, multiply the pulse rate in 15 seconds by 4 to get the pulse rate per minute: 19 · 4 = 76.
Example: Four businesses share the cost of purchasing a building valued at $5,000,000. If all four businesses pay equal amounts, how much would each business have to pay?
Answer: $5,000,000 ÷ 4 = $1,250,000.
Example: Given the temperature on the Fahrenheit scale is 41 degrees, what is the corresponding temperature in degrees on the Celsius scale?
Formula: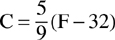 
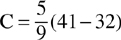. Perform the subtraction in the parentheses first.
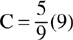
C = 5 degrees
Example: Given the temperature on the Celsius scale is 20 degrees, what is the corresponding temperature in degrees on the Fahrenheit scale?
Formula: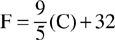 
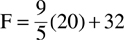
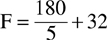
F = 36 + 32
F = 68 degrees
Example: How much 20% acid solution should be added to 50 liters of 45% acid solution to obtain a 30% acid solution?
Let x = amount of 20% (0.20) acid solution
0.45(50) = amount of acid in 50 liters of 45% acid solution
(50 + x) = total amount of acid solution
0.30(50 + x) = amount of acid in 30% (0.30) acid solution
Therefore 0.20x + 0.45(50) = 0.30(50 + x)
Multiply terms in parentheses first: 0.20x + 22.50 = 15 + 0.30x
Add/subtract like terms and bring the variable over to one side of the equation.
7.50 = 0.10x
75 liters = x = amount of 20% acid solution to be added.
Example: The sum of two consecutive integers is 47. What are the numbers?
Let x = the first number and (x + 1) = the second number.
Therefore
x + (x + 1) = 47
2x + 1 = 47
2x = 46
x = 23 = the first number
(x + 1) = 24 = the second number
Example: The sum of two numbers is 60. One number is four more than the other number. Find the two numbers.
Let x = the smaller number and (x + 4) = the larger number
Therefore
x + (x + 4) = 60
2x + 4 = 60
2x = 56
x = 28 = the smaller number
(x + 4) = 32 = the larger number
To average a number of values, take the sum of all the values and divide the sum by the total number of values.
Example: Find the average of the following numbers: 10, 20, 50, 25, and 75.
Example: A student has grades of 68, 70, 75, and 80. What will the next grade have to be for the student to obtain a 75 average?
Let the next grade = x
Therefore there will be a total of 5 grades and
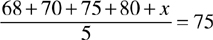
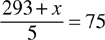
Multiply both sides by 5: 293 + x = 375
Subtract 293 from each side: x = 82
Example: Veteran firefighter John is twice as old as firefighter Joyce, and Joyce is five years older than probationary firefighter Jane. The sum of their ages is 95. What are the ages of all three fire fighters?
Let x = Joyce’s age
2x = John’s age
x – 5 = Jane’s age
Therefore
x + (2x) + (x – 5) = 95
x + 2x + x – 5 = 95
4x – 5 = 95
4x = 100
x = 25 = Joyce’s age
2x = 50 = John’s age
x – 5 = 20 = Jane’s age
Note: If it takes x hours to perform a task,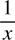 
of the job is done each hour.
Example: Probationary firefighter John can clean all the hose on the apparatus by himself in six hours. Veteran firefighter Raymond can complete the task in only four hours. If they work together, how long will it take?
x = time it takes to perform the work together.
John does 
the work in one hour.
Raymond does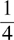 
the work in one hour.
Note: If several persons work together, the amount of work done is assumed to be the sum of the individual amounts.
Therefore
Find a common denominator (24x) by multiplying the denominators.
24 = 6x + 4x
24 = 10x
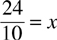
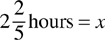
It will take John and Raymond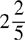 
hours, or 2 hours and 24 minutes, working together.
Example: Randy, a new recruit, can wash the fire apparatus alone in 60 minutes. If Randy works together with firefighter Clay, they can wash the apparatus in 20 minutes. How long would Clay need to wash the fire apparatus by himself?
Note: Use the formula W (Work done) = r (rate) · t (time). Basic-level work problems usually have W equal to 1.
Therefore
W =r · t and 
Let W = 1 (job of washing the fire apparatus)
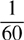= rate at which Randy performs the work
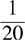= rate at which both Randy and Clay perform the work
= rate at which Clay performs the work
When we look at the relationship between distance (d), rate (r), and time (t), we can use the formula: d = rt to find the answer not only for distance but for rate of speed and time as well.
d = r · t and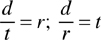 
Note: If in a word problem, parts of the trip are at different rates of speed, then to find the total time or total distance you must separate the parts of the trip.
Example: A plane can fly at a rate of 400 miles per hour (mph) from point A to point B, a distance of 1,600 miles. A high-speed train, however, makes the same trip back from point B to point A at a rate of speed of 160 mph. How many hours was the whole trip to and from points A and B?
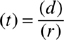
(t) going = 1,600 miles ÷ 400 mph = 4 hours
(t) returning = 1,600 miles ÷ 160 mph = 10 hours
Total (t) of whole trip = 14 hours
Example: A man can walk 4 mph in a still wind. When a favorable wind is at his back he can walk 15 miles in 3 hours. How fast is the wind?
Note: Use the formula: d = r · t
(r) = wind speed
(r + 4) = speed walking with wind at his back
15 miles = (r + 4) (3 hours) = 3r + 12
15 = 3r + 12
3 = 3r
1 mph = r
Example: An automobile travels through an intersection going north at 30 mph. Ten minutes later, a second automobile passes through the same intersection traveling in the same direction going 60 mph. How long will it take for the second automobile to overtake the first automobile?
Note: Use the formula: d = r · t
Let the first automobile = (30 mph) 
10 minute head start at 30 mph
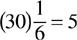miles traveled prior to second automobile reaching same intersection
The second automobile is gaining at a rate of 60 mph – 30 mph = 30 mph
How long (t) will the second automobile gaining at a rate (r) of 30 mph take to cover the (d) 5 mile head start of the first automobile?
d = r · t
5 = 30 (t) Divide both sides of the equation by 30
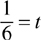
of an hour = 10 minutes = t = time required for the second automobile to overtake the first automobile
Example: Two trains pass in the night. One train is traveling west at 60 mph while the second train is going east at 80 mph. When will the trains be 420 miles apart?
Note: Use the formula: d = r · t
Note: When objects are moving in opposite directions, regardless of whether the objects are moving toward each other or away from each other, the rate at which the distance between them is changing is the sum of their individual rates.
Therefore 60 mph + 80 mph = 140 mph
Let
t = number of hours the trains will travel after passing each other
420 miles = 140 mph · t
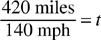divide by 140 on both sides of the equation to isolate the variable
3 hours = t = number of hours trains will travel after passing each other to be 420 miles apart
Example: Lance has $10 in quarters and dimes. He has a total of 55 coins. How many of each coin does he have?
Let x = number of dimes; 0.10x = dollar amount in dimes
55 – x = number of quarters; 0.25(55 – x) = dollar amount in quarters
Therefore
0.10x + 0.25(55 – x) = 10
0.10x + 13.75 – 0.25x = 10
Add/subtract like terms: –0.15x = –3.75
Divide both sides by 0.15: –x = –25
Divide both sides by –1
x = 25 = number of dimes
55 – x = 30 = number of quarters
Check:
25 dimes × 0.10 = $2.50
30 quarters × 0.25 = $7.50
Total: 55 coins = $10.00
Example: Senior paramedic Kathy earns two times more per hour than Eric, a junior paramedic, while Eric earns $4 more per hour than EMT Alex. Together they earn $48 per hour. How much is each medic’s hourly wage?
Let x = Alex; (x + 4) = Eric; 2(x + 4) = Kathy
Therefore
x + (x + 4) + 2(x + 4) = 48
x + x + 4 + 2x + 8 = 48
4x + 12 = 48
4x = 36
x = 9 = Alex’s hourly wage
(x + 4) = 13 = Eric’s hourly wage
2(x + 4) = 26 = Kathy’s hourly wage
Example: A $200 rebar cutter is reduced 20% for a catalog sale. What will be the sale price?
Let x = sale price
$200 = original price
(200)(0.20) = original price reduced 20%
Therefore
(200) – (200) (0.20) = x
200 – 40 = x
$160 = x = sale price
Example: Dave’s monthly budget is $2,400. His monthly rent is $600. What percent of his monthly budget is spent on rent?
Use formula: % = Part ÷ Whole · 100
Therefore
% = 600 ÷ 2,400 · 100
% = 0.25 · 100 = 25%
Use this simple formula to compute interest on dollars at an interest rate percent per year for a given number of years.
i = prt
where i = interest, p = principal, r = rate, and t = time
Example: What is the interest on $200 invested at 6% for two months?
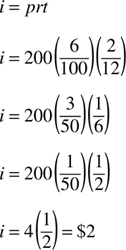
Example: Quinn deposits $3,500 into two savings deposit accounts. One account yields 4.5% annual earnings, while the second account yields 5.0%. Total interest earnings for the first year for both accounts is $180.00. How much money did Quinn deposit in each account?
Let x = account yielding 4.5% (0.045)
(3,500 – x) = account yielding 5.0% (0.050)
Therefore
0.045x + 0.050(3,500 – x) = 180
Multiply terms in parentheses first: 0.045x + 175 – 0.050x = 180
Add/subtract like terms: 0.005x = 5
Divide both sides by 0.005:
x = $1,000 deposited into 4.5%-yielding account
(3,500 – x) = $2,500 deposited into 5%-yielding account
Example: If a die is rolled once, determine the probability of rolling a 3.
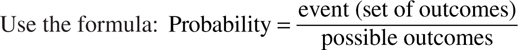
Therefore
Example: A deck of cards contains 52 cards, 13 of which are from each of 4 suits. If a card is randomly flipped over after a thorough shuffling, what is the probability that the suit will be a diamond?
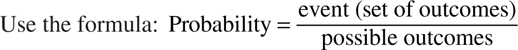
Therefore
Example: An ice cream cone comes in eight flavors with five possible combinations of toppings. How many different ice cream cones can be made with one flavor of ice cream and one topping?
Note: Rather than list the entire sample of all possible combinations, use the simple multiplication of factors.
Therefore 8 × 5 = 40 different ice cream cones can be made.
Example: In a classroom of 48 students, the ratio of passing grades to failing grades is 8 to 4. How many of the students had failing grades?
Let 8 passing grades + 4 failing grades = 12 (representative set).
Therefore 
of the class failed.
students had failing grades.
Example: An automobile travels 180 miles using 9 gallons of gasoline. Express the terms as a ratio in its simplest form to determine the miles traveled per gallon.
180:9 Convert to a fraction: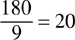 
Simplify the ratio: 20 miles per gallon
Example: Find the unknown value in the proportion: 7:x = 3:6
Convert to fraction form: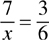 
Multiply the means and the extremes: 3x = 42
Isolate the variable by dividing by 3 on both sides of the equation:
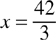
x = 14
Example: A wooden floor joist weighs 120 pounds and is 10 feet long. What is the weight of a similar floor joist that is 8 feet long?
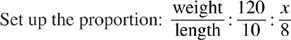
Multiply the means and the extremes:
10x = 120(8)
10x = 960
Isolate the variable by dividing by 10 on both sides of the equation:
x = 96 pounds
Geometry, one of the oldest branches of mathematics, is the study of shapes. The properties of points, lines, surfaces, and solids were first recognized by the early Babylonians and Egyptians over 4,000 years ago, and the rules of geometry helped in the construction of the pyramids.
This section is a very much abbreviated review of geometry. It focuses on the basics of geometry that will prove useful in answering mathematical questions dealing with the measurement of length, angles, perimeter, surface area, area, and volume. These measurements and calculations are useful to firefighters when performing their duties.
Point—In mathematics, a point represents position. It has no size or dimension. A point is represented by a dot followed by a capital letter.
Example: · A
Line—A line contains at least two points. It is a one-dimensional, straight line figure that extends indefinitely in two opposite directions. A line has no width. It is represented by arrowheads at both ends to denote that it has no endpoints. The arrowheads are placed above two arbitrary points on the line.
Example: 
Example: 
Line segment—A line segment is a one-dimensional set of points containing point A and point B and all the points lying between A and B. A line segment has a finite length and does not extend forever.
Example: 
Ray—A ray is drawn as a one-dimensional, straight line that has one endpoint. A ray is represented by an arrow starting at an endpoint and a designated point that the line passes through.
Example: 
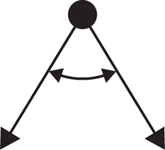
The intersection of two rays with a common endpoint forms an angle. The symbol for angle is ∠.
Acute angle—An angle that measures less than 90°.
Right angle—An angle that measures exactly 90°. All right angles are equal.
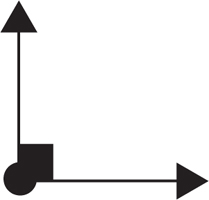
Obtuse angle—An angle that measures more than 90° but less than 180°.
Straight angle—An angle whose sides are opposite rays and that measures exactly 180°. All straight angles are equal.
Pairs of angles may have several different relationships.
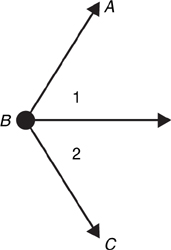
Adjacent angles—Two angles that share a common side and endpoint (vertex), but the rays are not common to both angles.
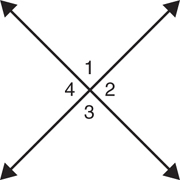
Vertical angles—Formed by intersecting lines whose sides form two pairs of opposite rays. Vertical angles are located across from each other in the corners of the “X” formed by the intersection of the lines. They are not adjacent. Vertical angles are always equal in measure.
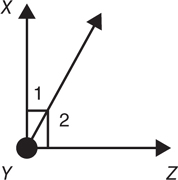
Complementary angles—Two angles the sum of whose measures is 90°. Complementary angles are placed so that they form perpendicular lines. Each angle is called the complement of the other.
Supplementary angles—Two angles the sum of whose measures is 180°. Supplementary angles are placed so that they form a straight line. Each angle is called the supplement of the other.
Equal angles—Angles that have the same measure.
Intersecting lines—Lines that share a common point are said to intersect, and the common point is termed the point of intersection.
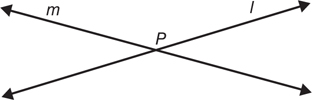
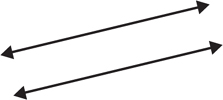
Parallel lines—Two lines are parallel when they lie in the same plane and do not share a common point. The symbol ≡ denotes two lines as being parallel.
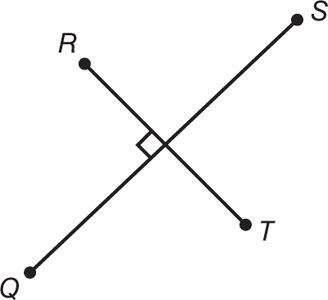
Perpendicular lines—When two lines intersect to form equal adjacent angles, the lines are said to be perpendicular. The angles formed are right angles (90°). The symbol ⊥ denotes two lines as being perpendicular.
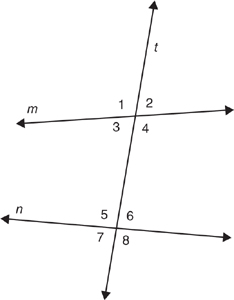
Transversal lines—A transversal is a line that intersects two or more other lines at different points. The transversal is generally denoted by the letter t.
Geometric shapes can be classified as one dimensional, two dimensional, or three dimensional. An example of a one-dimensional object is a circle. Common two-dimensional objects—a plane, a polygon, a parallelogram, a rhombus, a trapezoid, and a square—have length or vertical length (height) and width, but they lack depth. Common three-dimensional objects—cube, cylinder, sphere, and cone—have depth in addition to length or vertical length (height) and width. Each object has its own formulas for calculating perimeter, area, and volume, if applicable.
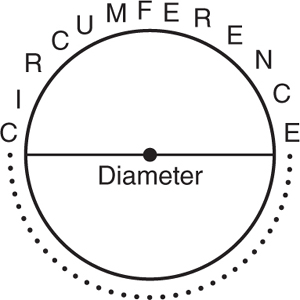
Perimeter (P) is the distance around a two-dimensional object. It is one dimensional and measured in linear units: millimeters (mm), centimeters (cm), meters (m), kilometers (km), inches (in), feet (ft), yards (yd), and so on. The perimeter of a circle is known as its circumference.
Area (A) is a physical quantity denoting the size of a part of a two-dimensional surface. It has units of distance squared.
Surface area (SA) is a summation of the areas of the exposed sides of a three-dimensional object. It has units of distance squared.
Volume (V) is how much space a three-dimensional object displaces. It is commonly measured in units of distance cubed such as cubic millimeters, centimeters, or meters or cubic inches, feet, or yards. When used to find how much a three-dimensional object can hold, it is called capacity. Common fluid measurements include milliliters, liters, ounces, and gallons.
The remainder of this section gives the formulas for calculating the perimeter, area, and volume of some common types of objects.
A circle is a planar, one-dimensional figure having a set of points all of which are the same distance, called a radius (r), from a fixed point (the center). The distance across a circle through the center is called the diameter (d), and it is twice the length of the radius (d = 2r). Other important terms to know are the chord, which is a line segment whose endpoints lie on the circle and the tangent line, which intersects the circle in exactly one point. Circles are closed curves, dividing the plane into an interior and an exterior.
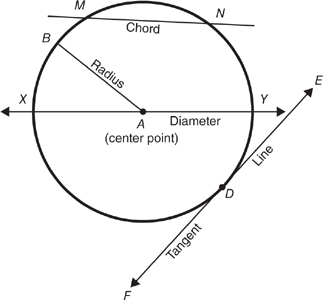
The circumference of a circle is the distance around or the length of a circle. It is basically the perimeter of the circle.
To determine the circumference (perimeter) of a circle, the mathematical constant known as pi (π) is used. It represents the ratio of the circumference to the diameter. When you divide the circumference by the diameter you get π or the approximate value of 3.14. Therefore, C/d = π. The circumference (C) of a circle is calculated by using the following formula:
C = π · d or C = 2 · π · r
The area of a circle can be calculated by multiplying π (π = 3.14) by the square of the radius. The formula is as follows:
A = πr2
A polygon is a closed, two-dimensional planar shape composed of a fixed number of straight line segments. Polygons are named according to the number of sides they have. Common examples include the triangle (3 sides), quadrilateral (4 sides), pentagon (5), hexagon (6), and octagon (8).
Quadrilaterals include a parallelogram, rhombus, trapezoid, and square.
The perimeter of irregularly shaped polygons is calculated by just adding all the lengths of the sides.
The perimeter of regular polygons (all angles and all sides coincide, or are congruent) is calculated by multiplying the number (n) of sides in the polygon by the length of a given side (s). The formula is: P = n · s.
The area of different polygons is calculated using different formulas that are given below.
A parallelogram is a four-sided, two-dimensional figure that has two sets of opposite parallel sides. The diagonals (straight line segments that cut across polygons joining two vertices) of a parallelogram bisect (cut in half) each other.
The perimeter of a parallelogram is calculated by adding the lengths of the four sides.
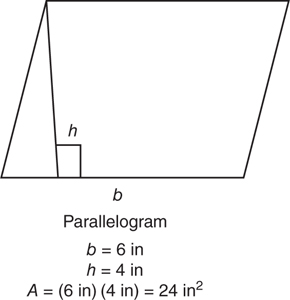
The area of a parallelogram is the product of the base and the height. The base (b) can be any side. The height of the trapezoid (h) is the perpendicular distance between the base and the opposite side. The area of a parallelogram can be calculated by using the formula:
A = b · h
A rhombus has a diamond shape. It is a four-sided, two-dimensional figure in which all sides are of equal length and opposite sides are parallel.
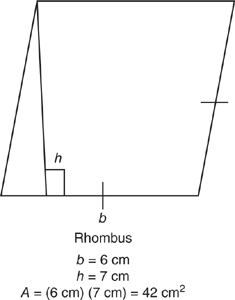
The perimeter of a rhombus is calculated using the same formula as used to get the perimeter of a regular polygon (P = n · s).
The area (A) of a rhombus can be calculated by multiplying the base (which can be any side) times the height (A = b · h) or by finding half of the product of the lengths of its diagonals, A = 1/2 (d1 · d2).
A trapezoid is a four-sided, two-dimensional shape with two parallel sides. The parallel sides of a trapezoid are called the bases (b1 and b2). The height of the trapezoid is the perpendicular distance between the bases (h).
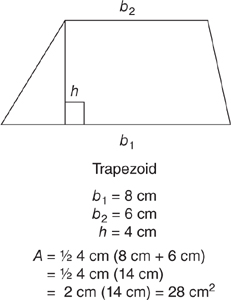
The perimeter of a trapezoid is calculated by adding the lengths of the four sides.
The area (A) of a trapezoid is calculated by adding the lengths of the two bases, multiplying that by the height, and then dividing by 2. The formula is: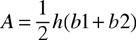 
The square is a four-sided, two-dimensional shape (polygon) with four equal length sides and four equal (right) interior angles. The diagonals of a square are also equal to each other and perpendicular to each other, and they are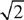 
(approximately 1.41) times the length of a side of a square.
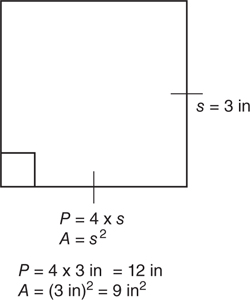
The perimeter of a square whose sides have length (s) is calculated by multiplying any given side by 4. The formula is: P = 4 · s.
The area of a square is calculated by raising any given side (s) to the second power. The formula is: A = s2.
A rectangle is a four-sided, two-dimensional shape (polygon) where all four of its interior angles are 90° (right) angles. The lengths of its diagonals are equal. It has two pairs of opposite sides that are of equal length. The length of the longer side is called the length (l) of the rectangle, and the length of the shorter side is its width (w).
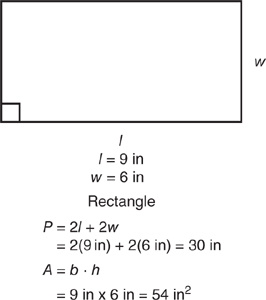
The perimeter of a rectangle is calculated by multiplying both the length and width by 2 and then adding the products. The formula is: P = 2l + 2w or P = 2 (l + w).
The area of a rectangle is the product of the base (length) and the height (width). The base (b) can be any side. Either side perpendicular to the base is called the height (h). The terms length and width can also be used in the same manner to find area. The formula is: A = b · h or A = l · w.
A triangle is a multisided, two-dimensional shape (polygon) consisting of three vertices and three sides that are straight line segments. The sum of the internal angles of a triangle measures 180°. Each of the points (A, B, C) shown in the triangle below is a vertex of the triangle.
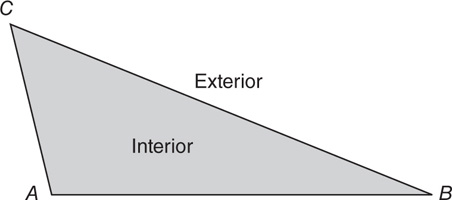
, , and are the sides of the triangle and ∠A, ∠B, and ∠C are the angles of the triangle.
Triangles can be categorized according to the length of their sides and by the size of their largest internal angle.
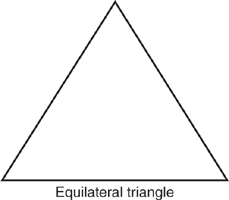
An equilateral triangle has all three sides of equal length. An equilateral triangle is also equiangular, in that all the internal angles are equal (60°).
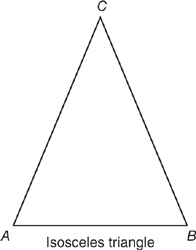
An isosceles triangle is a triangle in which at least two sides are of equal length. In the isosceles triangle, C is the vertex, ∠C is the vertex angle, is the base, and ∠A and ∠B are the base angles of the triangle. ∠A and ∠B are equal.
In a scalene triangle all sides of the triangle are of different lengths and the internal angles of the triangle are all different.
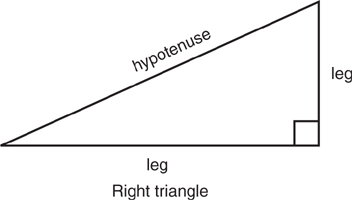
A right triangle has one interior right (90°) angle. The side opposite the right angle is called the hypotenuse and the other two sides are the legs.
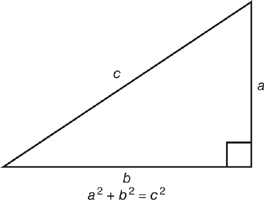
The relationship between the lengths of the legs and the length of the hypotenuse of a right triangle is stated in the Pythagorean theorem. Named for the Greek mathematician Pythagoras (circa 585–500 BC), the Pythagorean theorem states that in any right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. Thus, if the legs of a right triangle are a and b and the hypotenuse is c, a2 + b2 = c2.
An obtuse triangle is a triangle with an interior angle greater than 90°.
An acute triangle is a triangle with all three interior angles less than 90°.
An equiangular triangle (which has sides of equal length as mentioned above) is a triangle having three equal (60°) interior angles.
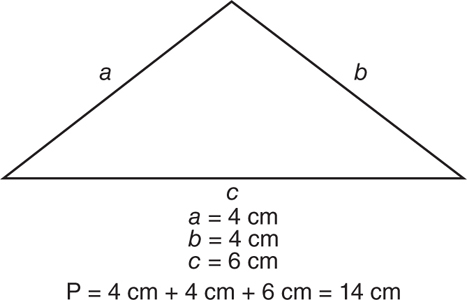
The perimeter of a triangle is calculated by adding the length of its three sides and has the formula: P = a + b + c.
The area of a triangle is calculated by multiplying the base by the height and then dividing by 2. The formula is: 
A cube is a three-dimensional figure having six square-shaped sides. The volume of a cube is calculated by raising the length of one side to the third power. The formula is: V = L3.
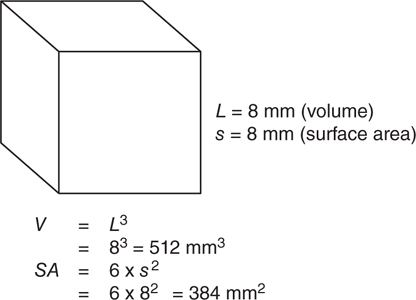
The surface area (SA) of a cube is calculated by multiplying 6 times the length of one side to the second power: SA = 6 · s2.
A rectangular prism is a three-dimensional figure having six rectangular sides.
The volume of a rectangular prism is found by multiplying the length by the width by the height, or V = l · w · h.
The surface area of a rectangular prism can be determined by the formula:
SA = 2lw + 2wh + 2lh
A cylinder is a three-dimensional figure having two congruent circular bases that are parallel.
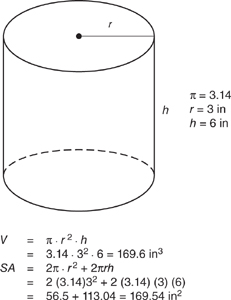
The volume of a cylinder is given by the formula: V = π · r2 · h.
The surface area of a cylinder is given by the formula:
SA = 2 πr2 + 2πrh
A sphere is a three-dimensional figure having all its points the same distance from its center.
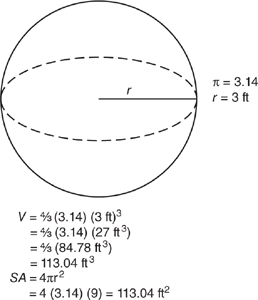
The volume of a sphere is given by the formula: 
The surface area of a sphere is given by the formula: SA = 4 · π · r2.
A cone is a three-dimensional figure having a circular base and a single vertex.
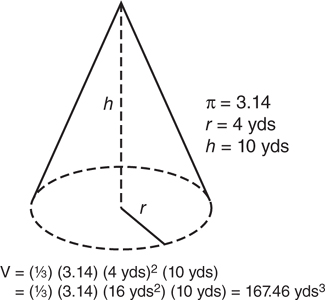
The volume of a cone is . h.
A square-based pyramid is a three-dimensional figure having a square base and four triangular-shaped sides.
The volume of a square-based pyramid is 
.
Circle the letter of your choice.
1. The mathematical symbol | | means
(A) is equal to
(B) ratio
(C) inequality
(D) absolute value of
2. Find the correct total: using the PEMDAS system to perform the mathematical operations in the correct sequence, evaluate the expression 8 + 7[5 + (9 – 2)2]
(A) 810
(B) 1,016
(C) 386
(D) 271
3. Subtracting one odd number from another odd number always leaves a remainder that is
(A) even
(B) odd
(C) either even or odd
(D) a negative number
4. Even numbers are numbers that when divided by 2
(A) leave no remainder
(B) always leave a remainder
(C) leave a remainder that is always an odd number
(D) always leave a negative result
5. Division by zero is
(A) possible only if the number being divided is odd
(B) possible only if the number being divided is even
(C) undefined and therefore has no meaning
(D) always equal to 1
6. A thermometer uses what type of numbers along its scale?
(A) absolute values
(B) ratios
(C) irrational
(D) signed
7. The absolute value of –8, represented by | –8 | is
(A) –8
(B) 64
(C) 8
(D) 4
8. –4 + (–3) =
(A) –7
(B) 1
(C) –1
(D) 7
9. (–9) (–2) =
(A) 7
(B) 18
(C) –18
(D) –7
10. (3)(–4)(–7)(–1)(9) =
(A) 756
(B) 675
(C) –675
(D) –756
11. (96) ÷ (–12) =
(A) –6
(B) –8
(C) 8
(D) 6
12. (–5)3 =
(A) –125
(B) 25
(C) –25
(D) 125
13. In the decimal number 42.089, the three numbers to the right of the decimal point indicate most accurately
(A) the number of tenths to be added to the whole number
(B) the number of hundredths to be added to the whole number
(C) the number of thousandths to be added to the whole number
(D) that the whole number should be rounded off to 43
14. 
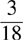equals which of the following decimals, rounded to a thousandth?
(A) 0.166
(B) 0.167
(C) 0.1666
(D) 0.1667
15. 4.726 + 32.88 =
(A) 80.140
(B) 37.154
(C) 37.606
(D) 37.506
16. 1.42 – 0.578 =
(A) 0.825
(B) 0.824
(C) 0.844
(D) 0.842
17. 6.9 × 3.72 =
(A) 25.876
(B) 25.668
(C) 24.998
(D) 25.658
18. 27.45 ÷ 0.3 =
(A) 9.15
(B) 91.5
(C) 93.0
(D) 9.45
19. 
(A)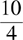 
(B)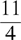 
(C)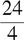 
(D)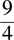 
20. Which of the following is not a prime number?
(A) 2
(B) 3
(C) 4
(D) 5
21. Which of the following lists the first four multiples of 9?
(A) 9, 18, 27, 36
(B) 9, 81, 729, 6,561
(C) 1, 9, 18, 27
(D) 1, 9, 81, 729
22. The fraction 14/35 reduced to lowest terms equals
(A) 5
(B)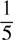 
(C)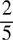 
(D) 7
23. Which of the following fractions is greater than 
?
(A)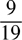 
(B)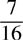 
(C)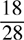 
(D) 
24. The sum of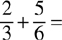 
(A)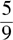 
(B)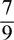 
(C)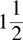 
(D) None of the above
25. 
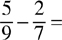
(A)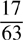 
(B) 
(C) 
(D)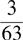 
26. The product of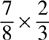 
reduced to its lowest terms equals
(A) 
(B) 
(C)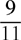 
(D) 
27. 
(A)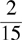 
(B)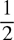 
(C) 1
(D)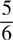 
28. 0.275 equals which percent?
(A) 00275%
(B) 0.0275%
(C) 2.75%
(D) 27.5%
29. 96.9% equals which decimal?
(A) 9.69
(B) 0.969
(C) 96.9
(D) None of the above
30. What is 38% of 25?
(A) 9
(B) 10
(C) 9.5
(D) 10.3
31. What percent of 22 is 13?
(A) 57.90
(B) 59.09
(C) 58.37
(D) 58.73
32. 16 is 47% of what number?
(A) 34
(B) 32
(C) 35
(D) 30
33. What is 33 increased by 72%?
(A) 57.67
(B) 56.84
(C) 23.76
(D) 56.76
34. What is 74 decreased by 9%?
(A) 6.66
(B) 67.58
(C) 6.80
(D) 67.34
35. 
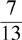equals which percent?
(A) 56.1%
(B) 53.8%
(C) 55.3%
(D) 57.2%
36. 34% equals which fraction, reduced to lowest terms?
(A)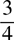 
(B)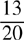 
(C)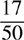 
(D)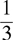 
37. In the arithmetic sequence of terms shown below, the difference between consecutive terms is constant. What is the absolute value of the constant interval between the terms?
4, 9, 14, 19, 24, 29, 34, 39, . . .
(A) 4
(B) 9
(C) 5
(D) 3
38. On a farm, there are 12 hens and 3 roosters. What is the ratio of hens to roosters in its simplest form?
(A) 12:3
(B) 3:12
(C) 1:3
(D) 4:1
39. Which ratio listed below is in its simplest form?
(A) 10:50
(B) 5:25
(C) 1:5
(D) None of the above
40. If four tickets to a show cost $18, which is the cost of 18 tickets?
(A) $78
(B) $81
(C) $88
(D) $76
41. For a house assessed at $20,000, the owner pays $500 in property tax. What should the property tax be on a house assessed at $35,000?
(A) $800
(B) $825
(C) $900
(D) $875
42. If a die is rolled once, what is the probability of rolling a 4 or higher number?
(A) 1/6
(B) 1/4
(C) 1/3
(D) 1/2
43. A movie theater sells three sizes of popcorn (small, medium, and large) with two choices of toppings (no butter and butter). How many different popcorn choices are available?
(A) 8
(B) 10
(C) 6
(D) 12
44. A state issues license plates containing all the letters of the alphabet as well as the numbers 0 through 9. If all of the letters and digits may be repeated, how many possible license plates can be issued with two letters followed by two numbers?
(A) 69,000
(B) 73,400
(C) 67,600
(D) 68,220
45. Factor the following algebraic expression: x2 – 3x – 18
(A) (x – 6) (x + 3)
(B) (x + 6) (x – 3)
(C) (x + 6) (x + 3)
(D) (x – 9) (x + 2)
46. 9x – (–3x) =
(A) 6x
(B) 12x
(C) 6x2
(D) 12x2
47. (2x)(6x)(3x) =
(A) 36x
(B) 36x2
(C) 12x2 + 3x + 36
(D) 36x3
48. (x)3 (x)2 (x)3 =
(A) x18
(B) x3
(C) x8
(D) None of the above
49. Solve: (92)3 =
(A) 95
(B) 93
(C) 96
(D) 92
50. 74 =
(A) 28
(B) 49
(C) 2,401
(D) 343
51. (–4)3 =
(A) –64
(B) 64
(C) –12
(D) 12
52. (8)0 =
(A) 0
(B) 1
(C) 8
(D) None of the above
53. 
(A) 6
(B) 8
(C) 9
(D) 18
54. Solve for x: 22x – 68 = 12 + 2x
(A) 2
(B) 4
(C) 6
(D) 8
55. Solve for x: 4(5x + 10) – 9(x + 3) = 68
(A) 3
(B) 4
(C) 5
(D) 2
56. A $400 firefighter bunker coat sells for how much money after it is discounted 5%?
(A) $350
(B) $370
(C) $380
(D) $395
57. Six pairs of work boots cost as much as three pairs of dress shoes. Which ratio compares the cost of work boots to the cost of dress shoes?
(A) 2:1
(B) 5:4
(C) 6:2
(D) 5:2
58. Find the pattern in the two columns below. Then solve for x.
(A) 24
(B) 26
(C) 28
(D) 32
59. 1.2 × 2.6 =
(A) 3.61
(B) 2.87
(C) 3.12
(D) 3.88
60. The sum of three consecutive multiples of 3 is 27. What is the largest of the three numbers?
(A) 18
(B) 15
(C) 12
(D) 9
61. If 30,000 candidates compete for firefighter jobs in a municipality, and only 15% of those candidates are expected to be hired over a four-year period, how many candidates will be hired?
(A) 3,000
(B) 1,500
(C) 6,000
(D) 4,500
62. A newly hired firefighter buys three uniformed shirts, four pairs of pants, and two pairs of work shoes at the quartermaster prior to the first day on the job. How many different outfits can be worn if an outfit consists of any shirt worn with any pair of pants and either pair of shoes?
(A) 8
(B) 9
(C) 12
(D) 24
63. If two packages of latex gloves cost $2.50, how much would five packages cost?
(A) $5.50
(B) $6.25
(C) $6.50
(D) $6.75
64. What is 75 decreased by 30%?
(A) 52.5
(B) 53
(C) 53.5
(D) 54.5
65. A train goes from City A to City B in three hours traveling at a uniform speed. The train goes 10 mph slower on the return trip, causing the journey to be an extra one-half hour longer. How far is City A from City B?
(A) 160 miles
(B) 210 miles
(C) 300 miles
(D) 320 miles
66. If 3 and x have the same average as 3, 7, and 20, what is the value of x?
(A) 14
(B) 17
(C) 20
(D) 22
67. A horse weighs 781 pounds, rounded to the nearest pound. Which weight listed below cannot be the actual weight of the horse?
(A) 780.6 pounds
(B) 781.1 pounds
(C) 781.4 pounds
(D) 781.7 pounds
68. A total of $360 is divided into equal shares. John receives four shares, David receives three shares, and Allen receives the remaining two shares. How much money did David get?
(A) $160
(B) $80
(C) $120
(D) $100
69. A basketball league has 100 players on eight different teams. Each team has at least 12 players. What is the largest possible number of players on any one team?
(A) 14
(B) 16
(C) 15
(D) 17
70. You have $80 to spend on a pair of shoes. The sales tax is 7%. What is the maximum amount the shoes can cost?
(A) $75.46
(B) $78.13
(C) $74.76
(D) $77.89
71. The formula for converting Celsius to Fahrenheit is 
. Use the formula to convert 10° Celsius into Fahrenheit degrees.
(A) 50
(B) 48
(C) 52
(D) 56
72. The formula for converting Fahrenheit to Celsius is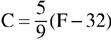 
. Use the formula to convert 77° Fahrenheit into Celsius degrees.
(A) 22
(B) 29
(C) 23
(D) 25
73. Right angles measure
(A) less than 90°
(B) more than 90°
(C) 90°
(D) 180°
74. Two lines are parallel when
(A) they intersect
(B) they form equal adjacent angles
(C) they do not share a common point
(D) the angles formed are right angles
75. The angles formed by two perpendicular lines are
(A) right angles
(B) acute angles
(C) obtuse angles
(D) more than 180°
76. The distance around a two-dimensional object that is measured in linear units is called the
(A) perimeter
(B) area
(C) surface area
(D) volume
77. The amount of space a three-dimensional object displaces is called the
(A) surface area
(B) perimeter
(C) area
(D) volume
78. The sum of the areas of the exposed sides of a three-dimensional object is called the
(A) perimeter
(B) volume
(C) surface area
(D) area
79. The radius of a circle is
(A) twice as long as the diameter
(B) half as long as the diameter
(C) the same length as the diameter
(D) None of the above
80. The distance around a circle is called
(A) π
(B) the area
(C) the circumference
(D) a chord
81. Find the approximate circumference of the circle. Use the formula: C = π · d or C = 2 · π · r.
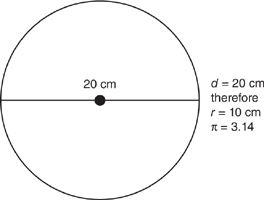
(A) 67.6 cm
(B) 65.3 cm
(C) 63.4 cm
(D) 62.8 cm
82. Find the area of the circle in question 81. Use the formula: A = π · r2.
(A) 3.14 cm2
(B) 31.4 cm2
(C) 314 cm2
(D) 3140 cm2
83. Find the perimeter (P) of the irregular polygon below.
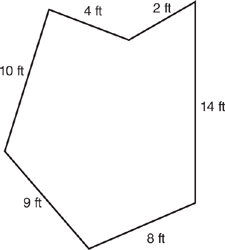
(A) 40 ft
(B) 47 ft
(C) 51 ft
(D) 53 ft
84. Find the perimeter of a regular six-sided polygon (hexagon) whose sides are 7 cm. Use the formula: P = ns.
(A) 28 cm
(B) 36 cm
(C) 42 cm
(D) 62 cm
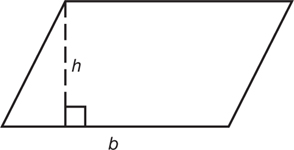
85. Find the height (h) of the parallelogram shown below whose area is 200 in2 and base is 20 in. Use the formula: A = b · h.
(A) 10 in
(B) 9 in
(C) 12 in
(D) 8 in
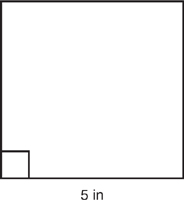
86. Find the perimeter of the square shown below with each side measuring 5 in. Use the formula: P = 4s.
(A) 16 in
(B) 20 in
(C) 24 in
(D) 25 in
87. Find the area of the square in question 86. Use the formula: A = s2.
(A) 16 in2
(B) 20 in2
(C) 24 in2
(D) 25 in2
88. Find the perimeter of the rectangle shown below having a length (l) of 24 cm and a width (w) of 14 cm. Use the formula: P = 2(l) + 2(w).
(A) 38 cm
(B) 62 cm
(C) 76 cm
(D) 91 cm
89. The sum of the internal angles of a triangle is
(A) 90°
(B) 120°
(C) 160°
(D) 180°
90. Triangles can be categorized according to the length of their sides. A triangle whose three sides are all different lengths is called
(A) equilateral
(B) scalene
(C) isosceles
(D) None of the above
91. Triangles can also be categorized according to the size of their largest interior angle. A triangle with three interior angles measuring less than 90° is called
(A) acute
(B) right
(C) obtuse
(D) None of the above
92. In an equilateral triangle, all three interior angles measure how many degrees?
(A) 30
(B) 45
(C) 60
(D) 65
93. Find the perimeter of the triangle shown below. Use the formula: P = a + b + c.
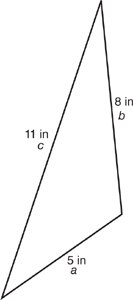
(A) 20 in
(B) 24 in
(C) 30 in
(D) 34 in
94. Find the area of the triangle shown below. Use the formula: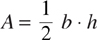 
.
(A) 36 in2
(B) 42 in2
(C) 48 in2
(D) 54 in2
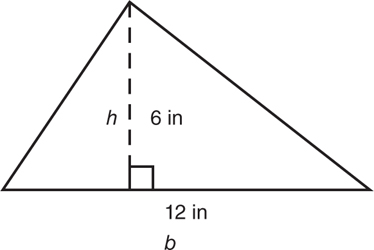
95. Find the volume of the cube shown below. Use the formula: V = L3.
(A) 81 cm3
(B) 729 cm3
(C) 917 cm3
(D) 936 cm3
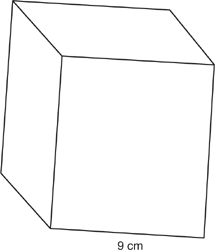
96. Find the surface area of the rectangular prism shown below. Use the formula: 2ab + 2bc + 2ac or 2lw + 2wh + 2lh.
(A) 456 in2
(B) 523 in2
(C) 544 in2
(D) 572 in2
97. Find the approximate volume of the cylinder shown below. Use the formula: V = π · r2 · h.
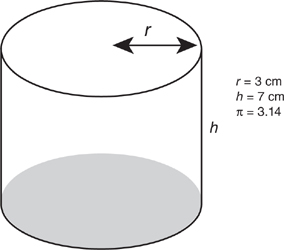
(A) 123.37 cm3
(B) 571.95 cm3
(C) 319.18 cm3
(D) 197.82 cm3
98. Find the approximate volume of the sphere shown below. Use the formula: 
.
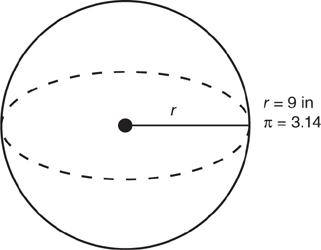
(A) 3,053 in3
(B) 3,180 in3
(C) 3,510 in3
(D) 3,795 in3
99. Find the approximate volume of the cone shown below. Use the formula: V = 1/3 π · r2 · h.
(A) 4,723 mm3
(B) 4,981 mm3
(C) 5,169 mm3
(D) 5,309 mm3
100. Find the approximate volume of the square-based pyramid shown below. Use the formula: V = 1/3 · A · h.
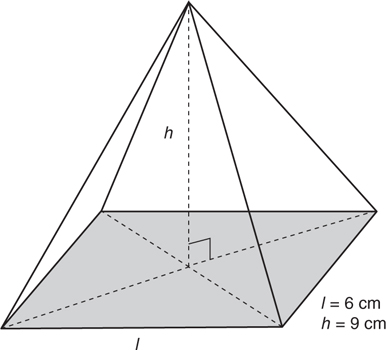
(A) 96 cm3
(B) 102 cm3
(C) 108 cm3
(D) 117 cm3
For answer explanations to the review questions in this section, refer to this book’s companion website.
1. D
2. C
3. A
4. A
5. C
6. D
7. C
8. A
9. B
10. D
11. B
12. A
13. C
14. B
15. C
16. D
17. B
18. B
19. B
20. C
21. A
22. C
23. C
24. C
25. A
26. A
27. D
28. D
29. B
30. C
31. B
32. A
33. D
34. D
35. B
36. C
37. C
38. D
39. C
40. B
41. D
42. D
43. C
44. C
45. A
46. B
47. D
48. C
49. C
50. C
51. A
52. B
53. C
54. B
55. C
56. C
57. A
58. C
59. C
60. C
61. D
62. D
63. B
64. A
65. B
66. B
67. D
68. C
69. B
70. C
71. A
72. D
73. C
74. C
75. A
76. A
77. D
78. C
79. B
80. C
81. D
82. C
83. B
84. C
85. A
86. B
87. D
88. C
89. D
90. B
91. A
92. C
93. B
94. A
95. B
96. C
97. D
98. A
99. D
100. C