

Deductive and inductive reasoning are two ways of arriving at a conclusion. Employers in the fire service are increasingly interested in finding young employees who exhibit good problem-solving skills and show sound judgment when decisions need to be made both in the workplace as well as on the fireground. The deductive and inductive thought processes are used to formulate opinions based upon incomplete information. They allow for analysis of facts and figures in an attempt to solve problems. The difference between deductive and inductive arguments is that a deductive argument’s conclusion is a guarantee from its reasoning, while the inductive argument’s conclusion is probable from its reasoning.
A deductive and inductive mindset may be helpful in solving problems that involve spatial reasoning or algebraic and number relationships, or to determine if a given argument is valid and identify errors in a given strategy or proof.
Deductive reasoning occurs when a person works from the more general information to the more specific. This is often called the “top-down” approach because the thinking starts at the top with a very broad range of information and works downward to a specific conclusion. It can begin with a theory concerning a point of interest. From there, a statement or prediction about the relationship between two or more variables is drawn. The prediction is then narrowed down further when observations are gathered in order to test the logic behind the thought process. Deductive reasoning is based on a general premise or assumption, and if the premise is true, then the reasoning will be valid. If the initial general premise is not accurate, however, results may be unexpected. Deductive reasoning, however, is logically valid, and it is the fundamental way in which mathematical facts are proven to be true. Researchers also utilize deductive reasoning to develop hypotheses (educated guesses) on how things work in the world we live in.
Deductive reasoning requires the problem solver to use at least two facts or rules in order to draw a valid conclusion based on given information. Deduction rules have two important components. They can be either universal or particular. Universal deduction rules apply to all groups to which they refer. Particular rules apply to only some groups or entities, not all to which they refer. An example of a universal statement about all groups of a given set would be: All horses have four legs. An example of a particular statement that applies to only some of a given group is: Some horses are thoroughbreds. You must differentiate between a universal rule and a particular rule, or you may make mistakes in your conclusions about the information you have read. If the rule is particular, the conclusion using deductive reasoning must always include the caveat: “maybe” or “perhaps.”
An example of deductive reasoning can be seen in this set of statements: Every day, I (a firefighter) leave home on my motorcycle to go to the firehouse at 0815 hours. Every day, the drive to the firehouse takes 20 minutes allowing me to be on time and ready to line up for roll call beginning at 0900 hours. Therefore, if I leave for work from home every day at 0815 hours, I will be on time and ready to line up for roll call.
This example of deductive reasoning makes logical sense, yet it cannot be relied upon to be perfectly accurate at all times. What if the motorcycle gets a flat tire on the way to work requiring the firefighter to get the motorcycle towed to a repair shop? The firefighter in this scenario will be late for roll call. This is why a hypothesis based upon deductive reasoning should not be completely relied upon. There is always the possibility for the initial premise to be wrong.
• In mathematics, if A = B and B = C, then A = C.
• All peaches are fruits, all fruits grow on trees; therefore, all peaches grow on trees.
• Humans are mortal, and I am a human, therefore I am mortal.
• All whales are mammals, all mammals have lungs; therefore all whales have lungs.
• All squares are rectangles, and all rectangles have four sides, so all squares have four sides.
• If John does not go to work and at work there is a party, then John will miss the party.
• All numbers ending in 0 or 5 are divisible by 5. The number 40 ends with a 0, so it is divisible by 5.
• Saturn is a planet, and all planets orbit a sun, therefore Saturn orbits a sun.
• All students who have at least 128 credits will earn a bachelor’s degree.
• It is dangerous to drive when streets are wet. It is raining now, so it is dangerous to drive now.
• Lizards are reptiles and reptiles are cold-blooded; therefore, lizards are cold-blooded.
• Acute angles are less than 90 degrees and this angle is 60 degrees, so this angle is acute.
• All noble gases are stable and argon is a noble gas, so argon is stable.
Inductive reasoning works the opposite way from deductive reasoning. The thought process moves from specific observations to broader generalities and theories. This is often known as the “bottom-up” approach. A person starts with specific observations and then begins to detect patterns and regularities. Inductive reasoning then formulates some tentative predictions in order to ultimately derive some general conclusions or theories. It will allow the thinker to make an educated guess based upon multiple observations.
Inductive reasoning is a discovery process where the observation of specific cases leads a person to assume strongly (though without absolute logical certainty) that some general principle is true. Although inductive reasoning can lead to false conclusions, it is a good tool for making predictions that may be verified using deductive reasoning.
An example of inductive reasoning can be seen in this set of statements: Today, I (a firefighter) left home on my motorcycle to go to the firehouse at 0815 hours and was on time to line up for roll call at 0900 hours. Therefore, every day that I leave my house to go to work at 0815 hours, I will arrive at the firehouse on time to line up for roll call.
Specific observations often do not correlate to valid general principles and therefore inductive reasoning is not logically valid. In the example above, firefighters often work weekends and holidays. If the day in question is a Sunday or holiday, the time frame to go from home to work may be misleading. Less traffic could allow the firefighter to get to work sooner than, let’s say, on a Monday at the beginning of the workweek. It is illogical to assume a general premise because one specific observation seems to suggest it.
• Joseph leaves for day camp at 0630 hours and is on time. Joseph assumes, then, that he will always be on time if he leaves at 0630 hours.
• Larry is a fire captain. All the fire captains I have known are nice. Therefore, Larry will be nice.
• All observed soccer players are short, so all soccer players are short.
• All firefighters at the fire academy are right-handed, so all firefighters are right-handed.
• All observed cats have fluffy fur, so all cats must have fluffy fur.
• All observed girls like to play with dolls. All girls, therefore, enjoy playing with dolls.
• The water in the ocean has always been approximately 70 degrees in August. It is August. The water will, therefore, be around 70 degrees.
• All observed firefighters are under 40 years old. Tom is a firefighter. Tom is under 40 years old.
• Barry is a football player. All observed football players are taller than 6 feet. Barry is assumed to be more than 6 feet tall.
• All observed wrestlers have a muscular build. Sam wrestles. It is assumed that Sam is muscular.
• All observed houses on Front Street are in poor structural condition. Charles lives on Front Street. The house that Charles lives in is in danger of collapse.
1. Use inductive reasoning to find the probable next term in the pattern:
5, 15, 20, 30, 35, 45, 50, 60, . . .
(A) 70
(B) 65
(C) 75
(D) 80
2. Using inductive reasoning, what is the probable next term in the pattern below?
3, 6, 9, 12, 15, . . .
(A) 16
(B) 17
(C) 18
(D) 19
For questions 3 through 8, indicate whether the statement is an example of deductive or inductive reasoning.
3. Since today is Wednesday, tomorrow will be Thursday._______
4. It has rained every Easter Sunday for six years; therefore, it will rain on Easter Sunday this year.__________
5. A woman observes a dozen roses, all of which are red. She concludes that all roses are red._________
6. Dan received a B grade on his first three science exams. He concludes he will earn a B on his next science exam._________
7. If 3x = 12, then x = 4.___________
8. All math teachers are over 5 feet, 8 inches tall. Professor Davis is a math teacher. Therefore, Mr. Davis is over 5 feet, 8 inches tall.__________
Answer questions 9 and 10 using True or False.
9. Conclusions made on inductive reasoning will always be true.__________
10. If one of your premises is false, your conclusion may be false.__________
Use inductive reasoning to determine the probable next number in each list for questions 11 through 13.
11. Probable next number in sequence: 3, 7, 11, 15, 19, 23, 27, . . .
(A) 28
(B) 29
(C) 30
(D) 31
12. Probable next number in sequence: 1, 1, 2, 3, 5, 8, 13, 21, . . .
(A) 28
(B) 30
(C) 34
(D) 38
13. Probable next number in sequence: 1, 2, 4, 8, 16, 32, . . .
(A) 64
(B) 58
(C) 56
(D) 54
14. Which of the following would make the best major premise for a deductive argument?
(A) No one knows if a comet will strike the Earth.
(B) There are no comets.
(C) Those who believe comets will strike the Earth have overexcited imaginations.
(D) Scientists have proven comets will not strike the Earth.
15. Change the following invalid conclusion to make it valid. In Harry’s home state you must be 16 years old to get a learner’s permit for driving an automobile. Harry’s sixteenth birthday is today. Therefore, Harry can now purchase an automobile.
(A) Harry can now drive an automobile.
(B) Harry can now get a driver’s license.
(C) Harry can now get a learner’s permit.
(D) Harry can now get a chauffeur’s license.
16. What is the four-digit number in which the first digit is one-third the second, the third is the sum of the first and second, and the last is three times the second?__________
17. To every question there is an answer. From this statement, which of the following is not possible?
(A) There is an answer that does not address any question.
(B) If there is a question then it has an answer.
(C) Wayne answered me although I did not ask a question.
(D) The teacher discussed questions that have no answer.
18. From the following two statements, what conclusion can be derived?
Only fish oil contains omega 3.
Only foods that contain omega 3 help with brain development.
(A) The only food that helps with brain development is fish oil.
(B) Only what contains omega 3 is fish oil.
(C) There are fish oils that help with brain development.
(D) All fish oils help with brain development.
19. How do researchers use deductive reasoning?
(A) To develop theories
(B) To develop hypotheses
(C) To create new ideas
(D) To control experiments
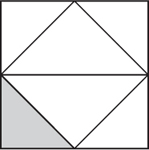
20. Use inductive reasoning to make an educated guess in drawing the next figure in the pattern going from left to right.

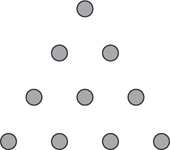
21. Draw the next set of dots on the right-hand side using inductive reasoning.

For questions 22 through 25, indicate whether the statement is an example of deductive or inductive reasoning.
22. I have never met a poodle with a nasty temperament. I bet there aren’t any in existence._________
23. Since some apples are red, and all apples are fruit, some fruit is red.__________
24. Obama will make a great president. After all he was a great state senator._________
25. It was the hot dog that made my stomach upset. What else could it be? I was not ill prior to eating it.__________
A combination of deductive and inductive reasoning is required to solve questions 26 through 30. Use your knowledge of logical thinking to determine the proper sequence of figures. Input the correct figure at the question mark (?) designation.
26.

27.

28.
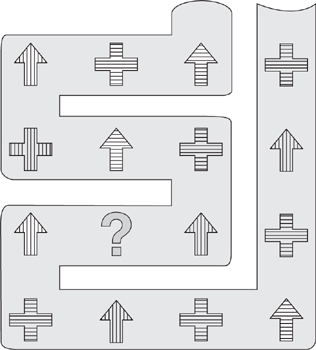
29.
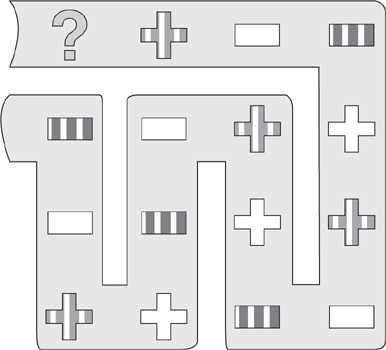
30.

1. B. It appears the numbers are sequentially increasing by 5 and 10.
2. C. It appears the numbers are increasing sequentially by 3.
3. Deductive
4. Inductive
5. Inductive
6. Inductive
7. Deductive
8. Deductive
9. False
10. False
11. D. It appears each number in the list is obtained by adding 4 to the previous number.
12. C. Beginning with the third number in the list, each number is obtained by adding the two previous numbers in the list.
13. A. It appears here that in order to obtain each number after the first, we must double the previous number.
14. C. It is stated as a generalization.
15. C
16. 1349
17. D
18. A. Combine the two statements provided in reverse: helps with brain development—contains Omega 3—fish oil.
19. B
20.
21.
22. Inductive
23. Deductive
24. Inductive
25. Inductive
26.

27.

28.
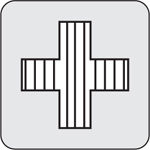
29.

30.
