2

Stock Market Prices Do Not Follow Random Walks: Evidence from a Simple Specification Test

SINCE KEYNES' (1936) NOW FAMOUS PRONOUNCEMENT that most investors' decisions “can only be taken as a result of animal spirits—of a spontaneous urge to action rather than inaction, and not as the outcome of a weighted average of benefits multiplied by quantitative probabilities,” a great deal of research has been devoted to examining the efficiency of stock market price formation. In Fama's (1970) survey, the vast majority of those studies were unable to reject the “efficient markets” hypothesis for common stocks. Although several seemingly anomalous departures from market efficiency have been well documented,¹ many financial economists would agree with Jensen's (1978a) belief that “there is no other proposition in economics which has more solid empirical evidence supporting it than the Efficient Markets Hypothesis.”

Although a precise formulation of an empirically refutable efficient markets hypothesis must obviously be model-specific, historically the majority of such tests have focused on the forecastability of common stock returns. Within this paradigm, which has been broadly categorized as the “random walk” theory of stock prices, few studies have been able to reject the random walk model statistically. However, several recent papers have uncovered empirical evidence which suggests that stock returns contain predictable components. For example, Keim and Stambaugh (1986) find statistically significant predictability in stock prices by using forecasts based on certain predetermined variables. In addition, Fama and French (1988) show that long holding-period returns are significantly negatively serially correlated, implying that 25 to 40 percent of the variation of longer-horizon returns is predictable from past returns.

In this chapter we provide further evidence that stock prices do not follow random walks by using a simple specification test based on variance estimators. Our empirical results indicate that the random walk model is generally not consistent with the stochastic behavior of weekly returns, especially for the smaller capitalization stocks. However, in contrast to the negative serial correlation that Fama and French (1988) found for longer-horizon returns, we find significant positive serial correlation for weekly and monthly holding-period returns. For example, using 1216 weekly observations from September 6, 1962, to December 26, 1985, we compute the weekly first-order autocorrelation coefficient of the equal-weighted Center for Research in Security Prices (CRSP) returns index to be 30 percent! The statistical significance of our results is robust to heteroskedasticity. We also develop a simple model which indicates that these large autocorrelations cannot be attributed solely to the effects of infrequent trading. This empirical puzzle becomes even more striking when we show that autocorrelations of individual securities are generally negative.

Of course, these results do not necessarily imply that the stock market is inefficient or that prices are not rational assessments of “fundamental” values. As Leroy (1973) and Lucas (1978) have shown, rational expectations equilibrium prices need not even form a martingale sequence, of which the random walk is a special case. Therefore, without a more explicit economic model of the price-generating mechanism, a rejection of the random walk hypothesis has few implications for the efficiency of market price formation. Although our test results may be interpreted as a rejection of some economic model of efficient price formation, there may exist other plausible models that are consistent with the empirical findings. Our more modest goal in this study is to employ a test that is capable of distinguishing among several interesting alternative stochastic price processes. Our test exploits the fact that the variance of the increments of a random walk is linear in the sampling interval. If stock prices are generated by a random walk (possibly with drift), then, for example, the variance of monthly sampled log-price relatives must be 4 times as large as the variance of a weekly sample. Comparing the (per unit time) variance estimates obtained from weekly and monthly prices may then indicate the plausibility of the random walk theory.² Such a comparison is formed quantitatively along the lines of the Hausman (1978) specification test and is particularly simple to implement.

In Section 2.1 we derive our specification test for both homoskedastic and heteroskedastic random walks. Our main results are given in Section 2.2, where rejections of the random walk are extensively documented for weekly returns indexes, size-sorted portfolios, and individual securities. Section 2.3 contains a simple model which demonstrates that infrequent trading cannot fully account for the magnitude of the estimated autocorrelations of weekly stock returns. In Section 2.4 we discuss the consistency of our empirical rejections with a mean-reverting alternative to the random walk model. We summarize briefly and conclude in Section 2.5.

2.1 The Specification Test

Denote by P_t the stock price at time t and define X_t ≡ In P_t as the log-price process. Our maintained hypothesis is given by the recursive relation

where µ is an arbitrary drift parameter and is the random disturbance term. We assume throughout that for all t, E[] = 0, where E[·] denotes the expectations operator. Although the traditional random walk hypothesis restricts the 's to be independently and identically distributed (IID) Gaussian random variables, there is mounting evidence that financial time series often possess time-varying volatilities and deviate from normality. Since it is the unforecastability, or uncorrelatedness, of price changes that is of interest, a rejection of the IID Gaussian random walk because of heteroskedasticity or nonnormality would be of less import than a rejection that is robust to these two aspects of the data. In Section 2.1.2 we develop a test statistic which is sensitive to correlated price changes but which is otherwise robust to many forms of heteroskedasticity and nonnormality. Although our empirical results rely solely on this statistic, for purposes of clarity we also present in Section 2.1.1 the sampling theory for the more restrictive IID Gaussian random walk.

2.1.1 Homoskedastic Increments

We begin with the null hypothesis H that the disturbances are independently and identically distributed normal random variables with variance 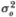; thus,

In addition to homoskedasticity, we have made the assumption of independent Gaussian increments. An example of such a specification is the exact discrete-time process X_t obtained by sampling the following well-known continuous-time process at equally spaced intervals:

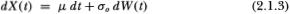
where dW(t) denotes the standard Wiener differential. The solution to this stochastic differential equation corresponds to the popular lognormal diffusion price process.

One important property of the random walk X_t is that the variance of its increments is linear in the observation interval. That is, the variance of X_t – X_t–2 is twice the variance of X_t – X_t–1. Therefore, the plausibility of the random walk model may be checked by comparing the variance estimate of X_t – X_t–1 to, say, one-half the variance estimate of X_t – X_t–2. This is the essence of our specification test; the remainder of this section is devoted to developing the sampling theory required to compare the variances quantitatively.

Suppose that we obtain 2n + 1 observations X₀, X₁,…, X_2n of X_t at equally spaced intervals and consider the following estimators for the unknown parameters µ and :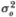

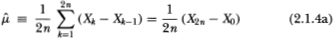
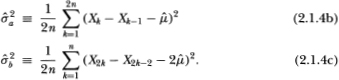
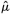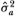The estimators and correspond to the maximum-likelihood estimators of the µ and 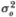parameters; 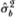of is also an estimator of 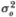but uses only the subset of n + 1 observations X₀, X₂ X₄,…, X_2n and corresponds formally to ½ times the variance estimator for increments of even-numbered observations. Under standard asymptotic theory, all three estimators are strongly consistent; that is, holding all other parameters constant, as the total number of observations 2n increases without bound the estimators converge almost surely to their population values. In addition, it is well known that both 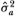and 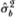possess the following Gaussian limiting distributions:

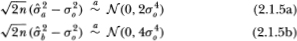
where indicates that the distributional equivalence is asymptotic. Of course, it is the limiting distribution of the difference of the variances that interests us. Although it may readily be shown that such a difference is also asymptotically Gaussian with zero mean, the variance of the limiting distribution is not apparent since the two variance estimators are clearly not asymptotically uncorrelated. However, since the estimator 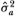is asymptotically efficient under the null hypothesis H, we may apply Hausman's (1978) result, which shows that the asymptotic variance of the difference is simply the difference of the asymptotic variances.³ If we define 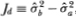, then we have the result

Using any consistent estimator of the asymptotic variance of J_d, a standard significance test may then be performed. A more convenient alternative test statistic is given by the ratio of the variances, J_r:⁴

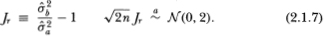
Although the variance estimator 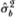is based on the differences of every other observation, alternative variance estimators may be obtained by using the differences of every qth observation. Suppose that we obtain nq + 1 observations X₀, X₁,…, X_nq, where q is any integer greater than 1. Define the estimators:

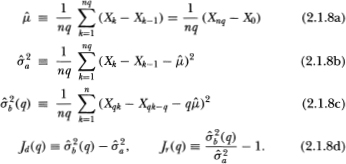
The specification test may then be performed using Theorem 2.1.⁵

Theorem 2.1. Under the null hypothesis H, the asymptotic distributions of J_d(q) and J_r(q) are given by

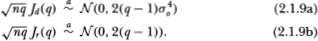
Two further refinements of the statistics J_d and J_r result in more desirable finite-sample properties. The first is to use overlapping qth differences of X_t, in estimating the variances by defining the following estimator of :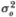

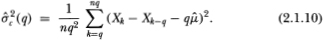
This differs from the estimator 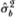(q) since this sum contains nq – q+1 terms, whereas the estimator 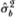(q) contains only n terms. By using overlapping qth increments, we obtain a more efficient estimator and hence a more powerful test. Using 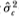(q) in our variance-ratio test, we define the corresponding test statistics for the difference and the ratio as

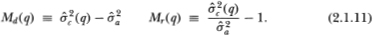
The second refinement involves using unbiased variance estimators in the calculation of the M-statistics. Denote the unbiased estimators as 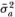and 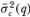, where

and define the statistics:

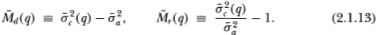
Although this does not yield an unbiased variance ratio, simulation experiments show that the finite-sample properties of the test statistics are closer to their asymptotic counterparts when this bias adjustment is made.⁶ Inference for the overlapping variance differences and ratios may then be performed using Theorem 2.2.

Theorem 2.2. Under the null hypothesis H, the asymptotic distributions of the statistics M_d(q), M_r(q), 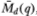, and 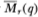are given by

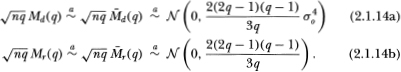
In practice, the statistics in Equations (2.1.14) may be standardized in the usual manner (e.g., define the (asymptotically) standard normal test statistic .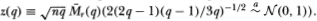

To develop some intuition for these variance ratios, observe that for an aggregation value q of 2, the M_r(q)-statistic may be reexpressed as

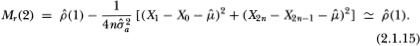
Hence, for q = 2 the M_r(q)-statistic is approximately the first-order autocorrelation coefficient estimator 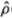(1) of the differences. More generally, it may be shown that

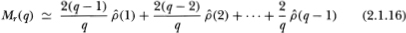
where 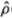(k) denotes the kth-order autocorrelation coefficient estimator of the first differences of X_t.⁷ Equation (2.1.16) provides a simple interpretation for the variance ratios computed with an aggregation value q: They are (approximately) linear combinations of the first q – 1 autocorrelation coefficient estimators of the first differences with arithmetically declining weights.⁸

2.1.2 Heteroskedastic Increments

Since there is already a growing consensus among financial economists that volatilities do change over time,⁹ a rejection of the random walk hypothesis because of heteroskedasticity would not be of much interest. We therefore wish to derive a version of our specification test of the random walk model that is robust to changing variances. As long as the increments are uncorrelated, even in the presence of heteroskedasticity the variance ratio must still approach unity as the number of observations increase without bound, for the variance of the sum of uncorrelated increments must still equal the sum of the variances. However, the asymptotic variance of the variance ratios will clearly depend on the type and degree of heteroskedasticity present. One possible approach is to assume some specific form of heteroskedasticity and then to calculate the asymptotic variance of 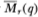under this null hypothesis. However, to allow for more general forms of heteroskedasticity, we employ an approach developed by White (1980) and by White and Domowitz (1984). This approach also allows us to relax the requirement of Gaussian increments, an especially important extension in view of stock returns' well-documented empirical departures from normality.¹⁰ Specifically, we consider the null hypothesis H*:¹¹

(Al) For all t, E() = 0, and 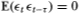for any τ ≠ 0.

(A2) {} is ø-mixing with coefficients ø(m) of size r/(2r – 1) or is α-mixing with coefficients α(m) of size r/(r – 1), where r > 1, such that for all t and for any τ ≥ 0, there exists some δ > 0 for which

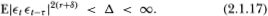
(A3)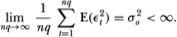

(A4) For all 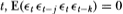for any nonzero j and k where j ≠ k.

 

This null hypothesis assumes that X_t possesses uncorrelated increments but allows for quite general forms of heteroskedasticity, including deterministic changes in the variance (due, for example, to seasonal factors) and Engle's (1982) ARCH processes (in which the conditional variance depends on past information).

Since 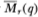still approaches zero under H*, we need only compute its asymptotic variance (call it θ(q)) to perform the standard inferences. We do this in two steps. First, recall that the following equality obtains asymptotically:

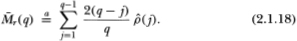
Second, note that under H* (condition 2.1.2) the autocorrelation coefficient estimators 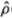(j) are asymptotically uncorrelated.¹² If we can obtain asymptotic variances δ(j) for each of the 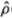(j) under H*, we may readily calculate the asymptotic variance θ(q) of 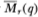as the weighted sum of the δ(j), where the weights are simply the weights in relation (2.1.18) squared. More formally, we have:

Theorem 2.3. Denote by δ(j) and θ(q) the asymptotic variances of 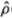(j) and 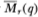, respectively. Then under the null hypothesis H* :

1. The statistics J_d(q), J_r(q), M_d(q), M_r(q), and 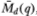, 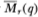all converge almost surely to zero for all q as n increases without bound.
2. The following is a heteroskedasticity-consistent estimator of δ(j) :

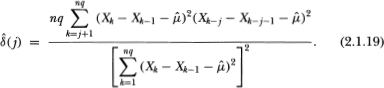
3. The following is a heteroskedasticity-consistent estimator of θ(q) :

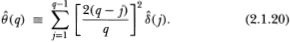
Despite the presence of general heteroskedasticity, the standardized test statistic 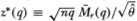is still asymptotically standard normal. In Section 2.2 we use the z*(q) statistic to test empirically for random walks in weekly stock returns data.

2.2 The Random Walk Hypothesis for Weekly Returns

To test for random walks in stock market prices, we focus on the 1216-week time span from September 6, 1962, to December 26, 1985. Our choice of a weekly observation interval was determined by several considerations. Since our sampling theory is based wholly on asymptotic approximations, a large number of observations is appropriate. While daily sampling yields many observations, the biases associated with nontrading, the bid-ask spread, asynchronous prices, etc., are troublesome. Weekly sampling is the ideal compromise, yielding a large number of observations while minimizing the biases inherent in daily data.

The weekly stock returns are derived from the CRSP daily returns file. The weekly return of each security is computed as the return from Wednesday's closing price to the following Wednesday's close. If the following Wednesday's price is missing, then Thursday's price (or Tuesday's if Thursday's is missing) is used. If both Tuesday's and Thursday's prices are missing, the return for that week is reported as missing.¹³

In Section 2.2.1 we perform our test on both equal- and value-weighted CRSP indexes for the entire 1216-week period, as well as for 608-week subperiods, using aggregation values q ranging from 2 to 16.¹⁴ Section 2.2.2 reports corresponding test results for size-sorted portfolios, and Section 2.2.3 presents results for individual securities.

2.2.1 Results for Market Indexes

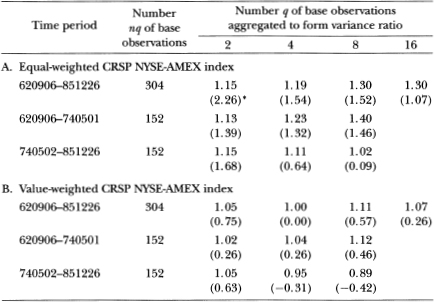
Tables 2.1a and 2.1b report the variance ratios and the test statistics z*(q) for CRSP NYSE-AMEX market-returns indexes. Table 2.1a presents the results for a one-week base observation period, and Table 2.1b reports similar results for a four-week base observation period. The values reported in the main rows are the actual variance ratios [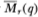 + 1], and the entries enclosed in parentheses are the z*(q) statistics.¹⁵

Panel A of Table 2.1a displays the results for the CRSP equal-weighted index. The first row presents the variance ratios and test statistics for the entire 1216-week sample period, and the next two rows give the results for the two 608-week subperiods. The random walk null hypothesis may be rejected at all the usual significance levels for the entire time period and all subperiods. Moreover, the rejections are not due to changing variances since the z*(q) statistics are robust to heteroskedasticity. The estimates of the variance ratio are larger than 1 for all cases. For example, the entries in the first column of panel A correspond to variance ratios with an aggregation value q of 2. In view of Equation (2.1.15), ratios with q = 2 are approximately equal to 1 plus the first-order autocorrelation coefficient estimator of weekly returns; hence, the entry in the first row, 1.30, implies that the first-order autocorrelation for weekly returns is approximately 30 percent. The random walk hypothesis is easily rejected at common levels of significance. The variance ratios increase with q, but the magnitudes of the z*(q) statistics do not. Indeed, the test statistics seem to decline with q; hence, the significance of the rejections becomes weaker as coarser-sample variances are compared to weekly variances. Our finding of positive autocorrelation for weekly holding-period returns differs from Fama and French's (1988) finding of negative serial correlation for long holding-period returns. This positive correlation is significant not only for our entire sample period but also for all subperiods.

Table 2.1a. Variance-ratio test of the random walk hypothesis for CRSP equal- and value-weighted indexes, for the sample period from, September 6, 1962, to December 26, 1985, and subperiods. The variance ratios 1+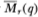 are reported in the main rows, with the heteroskedasticityrobust test statistics z*(q) given in parentheses immediately below each main row. Under the random walk null hypothesis, the value of the variance ratio is 1 and the test statistics have a standard normal distribution (asymptotically). Test statistics marked with asterisks indicate that the corresponding variance ratios are statistically different from 1 at the 5 percent level of significance.

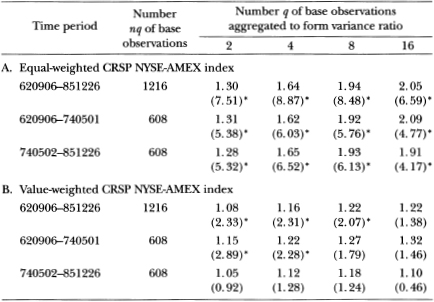
The rejection of the random walk hypothesis is much weaker for the value-weighted index, as panel B indicates; nevertheless, the general patterns persist: the variance ratios exceed 1, and the z*(q) statistics decline as q increases. The rejections for the value-weighted index are due primarily to the first 608 weeks of the sample period.

Table 2.1b. Market index results for a four-week base observation period

Variance-ratio test of the random walk hypothesis for CRSP equal- and value-weighted indexes, for the sample period from September 6, 1962, to December 26, 1985, and subperiods. The variance ratios 1 + 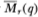are reported in the main rows, with the heteroskedasticity-robust test statistics z*(q) given in parentheses immediately below each main row. Under the random walk null hypothesis, the value of the variance ratio is 1 and the test statistics have a standard normal distribution (asymptotically). Test statistics marked with asterisks indicate that the corresponding variance ratios are statistically different from 1 at the 5 percent level of significance.

Table 2.1b presents the variance ratios using a base observation period of four weeks; hence, the first entry of the first row, 1.15, is the variance ratio of eight-week returns to four-week returns. With a base interval of four weeks, we generally do not reject the random walk model even for the equal-weighted index. This is consistent with the relatively weak evidence against the random walk that previous studies have found when using monthly data.

Although the test statistics in Tables 2.1a and 2.1b are based on nominal stock returns, it is apparent that virtually the same results would obtain with real or excess returns. Since the volatility of weekly nominal returns is so much larger than that of the inflation and Treasury-bill rates, the use of nominal, real, or excess returns in a volatility-based test will yield practically identical inferences.

2.2.2 Results for Size-Based Portfolios

An implication of the work of Keim and Stambaugh (1986) is that, conditional on stock and bond market variables, the logarithms of wealth relatives of portfolios of smaller stocks do not follow random walks. For portfolios of larger stocks, Keim and Stambaugh's results are less conclusive. Consequently, it is of interest to explore what evidence our tests provide for the random walk hypothesis for the logarithm of size-based portfolio wealth relatives.

We compute weekly returns for five size-based portfolios from the NYSE-AMEX universe on the CRSP daily returns file. Stocks with returns for any given week are assigned to portfolios based on which quintile their market value of equity is in. The portfolios are equal-weighted and have a continually changing composition.¹⁶ The number of stocks included in the portfolios varies from 2036 to 2720.

Table 2.2 reports the 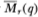test results for the size-based portfolios, using a base observation period of one week. Panel A reports the results for the portfolio of small firms (first quintile), panel B reports the results for the portfolio of medium-size firms (third quintile), and panel C reports the results for the portfolio of large firms (fifth quintile). Evidence against the random walk hypothesis for small firms is strong for all time periods considered; in panel A all the z*(q) statistics are well above 2.0, ranging from 6.12 to 11.92. As we proceed through the panels to the results for the portfolio of large firms, the z*(q) statistics become smaller, but even for the large-firms portfolio the evidence against the null hypothesis is strong. As in the case of the returns indexes, we may obtain estimates of the first-order autocorrelation coefficient for returns on these size-sorted portfolios simply by subtracting 1 from the entries in the q = 2 column. The values in Table 2.2 indicate that the portfolio returns for the smallest quintile have a 42 percent weekly autocorrelation over the entire sample period! Moreover, this autocorrelation reaches 49 percent in subperiod 2 (May 2, 1974, to December 26, 1985). Although the serial correlation for the portfolio returns of the largest quintile is much smaller (14 percent for the entire sample period), it is statistically significant.

Table 2.2. Variance-ratio test of the random walk hypothesis for size-sorted portfolios, for the sample period from September 6, 1962, to December 26, 1985, and subperiods. The variance ratios 1 + 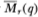are reported in the main rows, with the heteroskedasticity-robust test statistics z*(q) given in parentheses immediately below each main row. Under the random walk null hypothesis, the value of the variance ratio is 1 and the test statistics have a standard normal distribution (asymptotically). Test statistics marked with asterisks indicate that the corresponding variance ratios are statistically different from 1 at the 5 percent level of significance.

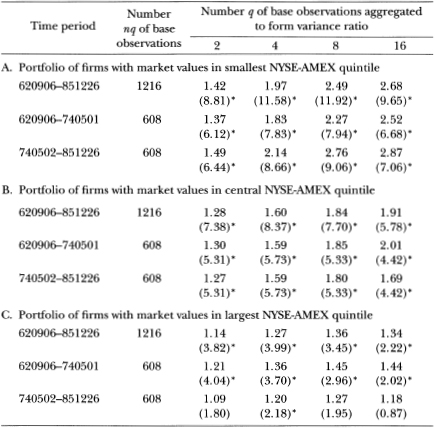
Using a base observation interval of four weeks, much of the evidence against the random walk for size-sorted portfolios disappears. Although the smallestquintile portfolio still exhibits a serial correlation of 23 percent with a z*(2) statistic of 3.09, none of the variance ratios for the largestquintile portfolio is significantly different from 1. In the interest of brevity, we do not report those results here but refer interested readers to Lo and MacKinlay (1987b).

The results for size-based portfolios are generally consistent with those for the market indexes. The patterns of (1) the variance ratios increasing in q and (2) the significance of rejections decreasing in q that we observed for the indexes also obtain for these portfolios. The evidence against the random walk hypothesis for the logarithm of wealth relatives of small-firms portfolios is strong in all cases considered. For larger firms and a one-week base observation interval, the evidence is also inconsistent with the random walk; however, as the base observation interval is increased to four weeks, our test does not reject the random walk model for larger firms.

2.2.3 Results for Individual Securities

For completeness, we performed the variance-ratio test on all individual stocks that have complete return histories in the CRSP database for our entire 1216-week sample period, yielding a sample of 625 securities. Owing to space limitations, we report only a brief summary of these results in Table 2.3. Panel A contains the cross-sectional means of variance ratios for the entire sample as well as for the 100 smallest, 100 intermediate, and 100 largest stocks. Cross-sectional standard deviations are given in parentheses below the main rows. Since the variance ratios are clearly not cross-sectionally independent, these standard deviations cannot be used to form the usual tests of significance; they are reported only to provide some indication of the cross-sectional dispersion of the variance ratios.

The average variance ratio for individual securities is less than unity when q = 2, implying that there is negative serial correlation on average. For all stocks, the average serial correlation is –3 percent, and –6 percent for the smallest 100 stocks. However, the serial correlation is both statistically and economically insignificant and provides little evidence against the random walk hypothesis. For example, the largest average z*(q) statistic over all stocks occurs for q = 4 and is –0.90 (with a cross-sectional standard deviation of 1.19); the largest average z*(q) for the 100 smallest stocks is –1.67 (for q = 2, with a cross-sectional standard deviation of 1.75). These results complement French and Roll's (1986) finding that daily returns of individual securities are slightly negatively autocorrelated.

For comparison, panel B reports the variance ratios of equal- and value-weighted portfolios of the 625 securities. The results are consistent with those in Tables 2.1 and 2.2; significant positive autocorrelation for the equal-weighted portfolio, and less significant positive autocorrelation for the value-weighted portfolio.

That the returns of individual securities have statistically insignificant autocorrelation is not surprising. Individual returns contain much company specific, or “idiosyncratic,” noise that makes it difficult to detect the presence of predictable components. Since the idiosyncratic noise is largely attenuated by forming portfolios, we would expect to uncover the predictable “systematic” component more readily when securities are combined. Nevertheless, the negativity of the individual securities' autocorrelations is an interesting contrast to the positive autocorrelation of the portfolio returns. Since this is a well-known symptom of infrequent trading, we consider such an explanation in Section 2.3.

Table 2.3. Means of variance ratios over all individual securities with complete return histories from September 2, 1962, to December 26, 1985 (625 stocks). Means of variance ratios for the smallest 100 stocks, the intermediate 100 stocks, and the largest 100 stocks are also reported. For purposes of comparison, panel B reports the variance ratios for equal- and value-weighted portfolios, respectively, of the 625 stocks. Parenthetical entries for averages of individual securities (panel A) are standard deviations of the cross-section of variance ratios. Because the variance ratios are not cross-sectionally independent, the standard deviation cannot be used to perform the usual significance tests; they are reported only to provide an indication of the variance ratios’ cross-sectional dispersion. Parenthetical entries for portfolio variance ratios (panel B) are the heteroskedasticity-robust z*(q) statistics. Asterisks indicate variance ratios that are statistically different from 1 at the 5 percent level of significance.

2.3 Spurious Autocorrelation Induced by Nontrading

Although we have based our empirical results on weekly data to minimize the biases associated with market microstructure issues, this alone does not ensure against the biases' possibly substantial influences. In this section we explicitly consider the conjecture that infrequent or nonsynchronous trading may induce significant spurious correlation in stock returns.¹⁷ The common intuition for the source of such artificial serial correlation is that small capitalization stocks trade less frequently than larger stocks. Therefore, new information is impounded first into large-capitalization stock prices and then into smaller-stock prices with a lag. This lag induces a positive serial correlation in, for example, an equal-weighted index of stock returns. Of course, this induced positive serial correlation would be less pronounced in a value-weighted index. Since our rejections of the random walk hypothesis are most resounding for the equal-weighted index, they may very well be the result of this nontrading phenomenon. To investigate this possibility, we consider the following simple model of nontrading.¹⁸

Suppose that our universe of stocks consists of N securities indexed by i, each with the return-generating process

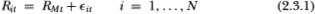
where R_Mt represents a factor common to all returns (e.g., the market) and is assumed to be an independently and identically distributed (IID) random variable with mean µ_M and varianc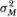e . The 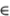_it term represents the idiosyncratic component of security i's return and is also assumed to be IID (over both i and t), with mean 0 and variance 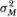. The return-generating process may thus be identified with N securities each with a unit beta such that the theoretical R² of a market-model regression for each security is 0.50.

Suppose that in each period t there is some chance that security i does not trade. One simple approach to modeling this phenomenon is to distinguish between the observed returns process and the virtual returns process. For example, suppose that security i has traded in period t – 1; consider its behavior in period t. If security i does not trade in period t, we define its virtual return as R_it (which is given by Equation (2.3.1)), whereas its observed return 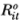is zero. If security i then trades at t+1, its observed return 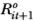is defined to be the sum of its virtual returns R_it and R_it+1; hence, nontrading is assumed to cause returns to cumulate. The cumulation of returns over periods of nontrading captures the essence of spuriously induced correlations due to the nontrading lag.

To calculate the magnitude of the positive serial correlation induced by nontrading, we must specify the probability law governing the nontrading event. For simplicity, we assume that whether or not a serucity trades may be modeled by a Bernoulli trial, so that in each period and for each security there is a probability p that it trades and a probability 1 – p that is does not. It is assumed that these Bernoulli trials are IID across securities and, for each security, are IID over time. Now consider the observed return 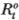at time t of an equal-weighted portfolio:

The observed return 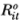for security i may be expressed as

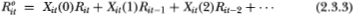
where X_it(j), j = 1, 2, 3,…are random variables defined as

The X_it(j) variables are merely indicators of the number of consecutive periods before t in which security j has not traded. Using this relation, we have

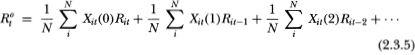
For large N, it may readily be shown that because the _it component of each security's return is idiosyncratic and has zero expectation, the following approximation obtains:

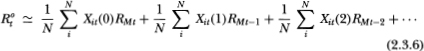
It is also apparent that the averages 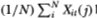become arbitrarily close, again for large N, to the probability of j consecutive no-trades followed by a trade; that is,

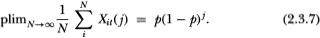
The observed equal-weighted return is then given by the approximation

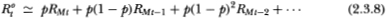
Using this expression, the general jth-order autocorrelation coefficient ρ(j) may be readily computed as

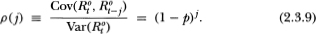
Assuming that the implicit time interval corresponding to our single period is one trading day, we may also compute the weekly (five-day) first-order autocorrelation coefficient of as

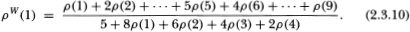
By specifying reasonable values for the probability of nontrading, we may calculate the induced autocorrelation using Equation (2.3.10). To develop some intuition for the parameter p, observe that the total number of secutities that trade in any given period t is given by the sum 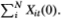Under our assumptions, this random variable has a binomial distribution with parameters (N, p); hence, its expected value and variance are given by Np and Np(1 – p), respectively. Therefore, the probability p may be interpreted as the fraction of the total number of N securities that trades on average in any given period. A value of .90 implies that, on average, 10 percent of the securities do not trade in a single period.

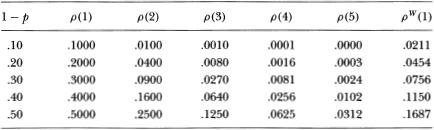
Table 2.4 presents the theoretical daily and weekly autocorrelations induced by nontrading for nontrading probabilities of 10 to 50 percent. The first row shows that when (on average) 10 percent of the stocks do not trade each day, this induces a weekly autocorrelation of only 2.1 percent! Even when the probability of nontrading is increased to 50 percent (which is quite unrealistic), the induced weekly autocorrelation is 17 percent.¹⁹ We conclude that our rejection of the random walk hypothesis cannot be attributed solely to infrequent trading.

Table 2.4. Spuriously induced autocorrelations are reported for nontrading probabilities 1 – p of 10 to 50 percent. In the absence of the nontrading phenomenon, the theoretical values of daily jth-order autocorrelations ρ(j) and the weekly first-order autocorrelation ρ^W(1) are all zero.

The positive autocorrelation of portfolio returns and the negative autocorrelation of individual securities is puzzling. Although our stylized model suggests that infrequent trading cannot fully account for the 30 percent autocorrelation of the equal-weighted index, the combination of infrequent trading and Roll's (1984a) bid-ask effect may explain a large part of the small negative autocorrelation in individual returns.

One possible stochastic model that is loosely consistent with these observations is to let returns be the sum of a positively autocorrelated common component and an idiosyncratic white-noise component. The common component induces significant positive autocorrelation in portfolios since the idiosyncratic component is trivialized by diversification. The white-noise component reduces the positive autocorrelation of individual stock returns, and the combination of infrequent trading and the bid-ask spread effects drives the autocorrelation negative. Of course, explicit statistical estimation is required in order to formalize such heuristics and, ultimately, what we seek is an economic model of asset prices that might give rise to such empirical findings. This is beyond the scope of this chapter, but it is the focus of current investigation.

2.4 The Mean-Reverting Alternative to the Random Walk

Although the variance-ratio test has shown weekly stock returns to be incompatible with the random walk model, the rejections do not offer any explicit guidance toward a more plausible model for the data. However, the patterns of the test's rejections over different base observation intervals and aggregation values q do shed considerable light on the relative merits of competing alternatives to the random walk. For example, one currently popular hypothesis is that the stock-returns process may be described by the sum of a random walk and a stationary mean-reverting component, as in Summers (1986) and in Fama and French (1988).²⁰ One implication of this alternative is that returns are negatively serially correlated for all holding periods. Another implication is that, up to a certain holding period, the serial correlation becomes more negative as the holding period increases.²¹ If returns are in fact generated by such a process, then their variance ratios should be less than unity when q = 2 (since negative serial correlation is implied by this process). Also, the rejection of the random walk should be stronger as q increases (larger z*(q) values for larger q).²² But Tables 2.1 and 2.2 and those in Lo and MacKinlay (1987b) show that both these implications are contradicted by the empirical evidence.²³ Weekly returns do not follow a random walk, but they do not fit a stationary mean-reverting alternative any better.

Of course, the negative serial correlation in Fama and French's (1988) study for long (three- to five-year) holding-period returns is, on purely theoretical grounds, not necessarily inconsistent with positive serial correlation for shorter holding-period returns. However, our results do indicate that the sum of a random walk and a mean-reverting process cannot be a complete description of stock-price behavior.

2.5 Conclusion

We have rejected the random walk hypothesis for weekly stock market returns by using a simple volatility-based specification test. These rejections cannot be explained completely by infrequent trading or time-varying volatilities. The patterns of rejections indicate that the stationary mean-reverting models of Shiller and Perron (1985), Summers (1986), Poterba and Summers (1988), and Fama and French (1988) cannot account for the departures of weekly returns from the random walk.

As we stated in the introduction, the rejection of the random walk model does not necessarily imply the inefficiency of stock-price formation. Our results do, however, impose restrictions upon the set of plausible economic models for asset pricing; any structural paradigm of rational price formation must now be able to explain this pattern of serial correlation present in weekly data. As a purely descriptive tool for examining the stochastic evolution of prices through time, our specification test also serves a useful purpose, especially when an empirically plausible statistical model of the price process is more important than a detailed economic paradigm of equilibrium. For example, the pricing of complex financial claims often depends critically upon the specific stochastic process driving underlying asset returns. Since such models are usually based on arbitrage considerations, the particular economic equilibrium that generates prices is of less consequence. One specific implication of our empirical findings is that the standard Black-Scholes pricing formula for stock index options is misspecified.

Although our variance-based test may be used as a diagnostic check for the random walk specification, it is a more difficult task to determine precisely which stochastic process best fits the data. The results of French and Roll (1986) for return variances when markets are open versus when they are closed add yet another dimension to this challenge. The construction of a single stochastic process that fits both short and long holding-period returns data is one important direction for further investigation. However, perhaps the more pressing problem is to specify an economic model that might give rise to such a process for asset prices, and this will be pursued in subsequent research.

Appendix A2
Proof of Theorems

Proof of Theorem 2.1

Under the IID Gaussian distributional assumption of the null hypothesis H, 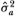and 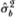of are maximum-likelihood estimators of σ₀² with respect to data sets consisting of every observation and of every qth observation, respectively (the dependence of 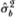on q is suppressed for notational simplicity). Therefore, it is well known that

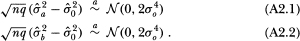
Since, under the null hypothesis H, 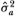is the maximum-likelihood estimator of σ₀² using every observation, it is asymptotically efficient. Therefore, following Hausman's (1978) approach, we conclude that the asymptotic variance of 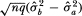is simply the difference of the asymptotic variances of 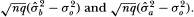Thus, we have

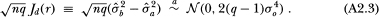
The asymptotic distribution of the ratio then follows by applying the “delta method” to the quantity 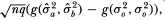where the bivariate function g is defined as g(u, v) ≡ v/u; hence,

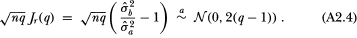
Proof of Theorem 2.2

To derive the limiting distributions of and 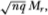we require the asymptotic distribution of 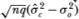(the dependence of 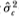on q is suppressed for notational convenience). Our approach is to reexpress this variance estimator as a function of the autocovariances of the (X_k – X_k–q) terms and then employ well-known limit theorems for autocovariances. Consider the quantity

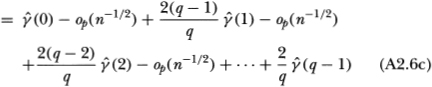
where 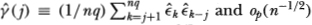denotes a quantity that is of an order smaller than 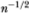in probability. Now define the (q × 1) vector 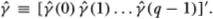A standard limit theorem for sample autocovariances 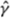of a stationary time series with independent Gaussian increments is (see, for example, Fuller, 1976, chap. 6.3)

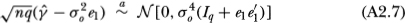
where e₁ is the (q × 1) vector and I_q is the identity matrix of order q. Returning to the quantity 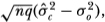we have

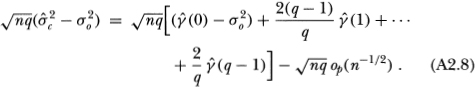
Combining Equations (A2.7) and (A2.8) then yields the following result:

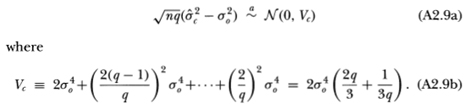
Given the asymptotic distributions (A2.1) and (A2.5), Hausman's (1978) method may be applied in precisely the same manner as in Theorem 2.1 to yield the desired result:

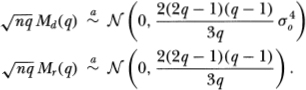
The distributional results for 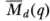and 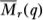follow immediately since asymptotically these statistics are equivalent to M_d(q) and M_r(q), respectively.

Proof of Theorem 2.3

1. We prove the result for 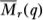; the proofs for the other statistics follow almost immediately from this case. Define the increments process as Y_t ≡ X_t − X_t–1 and define 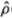(τ) as

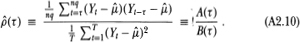
Consider first the numerator A(τ) of 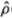(τ):

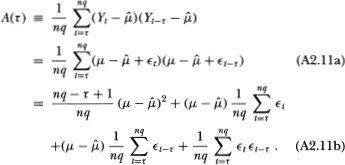
Since converges almost surely (a.s.) to µ, the first term of Equation (A2.11b) converges a.s. to zero as nq → ∞. Moreover, under condition 2.1.2 it is apparent that {} satisfies the conditions of White's (1984) corollary 3.48; hence, H*'s condition 2.1.2 implies that the second and third terms of (A2.11b) also vanish a.s. Finally, because 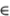_{t 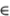t–τ} is clearly a measurable function of the 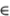's, {ε_{t 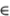t–τ}}, is also mixing with coefficients of the same size as {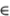_t}. Therefore, under condition 2.1.2, corollary 3.48 of White (1984) may also be applied to {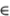_{t 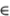t–τ}}, for which condition 2.1.2 implies that the fourth term of Equation (A2.11b) converges a.s. to zero as well. By similar arguments, it may also be shown that

Therefore, we have 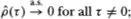hence, we conclude that

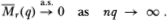
2. By considering the regression of increments 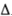X_t on a constant term and lagged increments 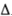X_t–j, this follows directly from White and Domowitz (1984). Taylor (1984) also obtains this result under the assumption that the multivariate distribution of the sequence of disturbances is symmetric.

3. This result follows trivially from Equation (2.1.14a) and condition 2.1.2.

---

¹See, for example, the studies in Jensen's (1978b) volume on anomalous evidence regarding market efficiency.

²The use of variance ratios is, of course, not new. Most recently, Campbell and Mankiw (1987), Cochrane (1987b, 1987c), Fama and French (1988), French and Roll (1986), and Huizinga (1987) have all computed variance ratios in a variety of contexts; however, these studies do not provide any formal sampling theory for our statistics. Specifically, Cochrane (1988), Fama and French (1988), and French and Roll (1986) all rely on Monte Carlo simulations to obtain standard errors for their variance ratios under the null. Campbell and Mankiw (1987) and Cochrane (1987c) do derive the asymptotic variance of the variance ratio but only under the assumption that the aggregation value q grows with (but more slowly than) the sample size T. Specifically, they use Priestley's (1981, page 463) expression for the asymptotic variance of the estimator of the spectral density of 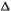X_t at frequency 0 (with a Bartlett window) as the appropriate asymptotic variance of the variance ratio. But Priestley's result requires (among other things) that q → ∞, T → ∞, and q/T → 0. In this chapter we develop the formal sampling theory of the variance-ratio statistics for the more general case.

Our variance ratio may, however, be related to the spectral-density estimates in the following way. Letting f (0) denote the spectral density of the increments 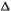X_t at frequency 0, we have the following relation:

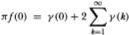
where γ (k) is the autocovariance function. Dividing both sides by the variance γ (0) then yields

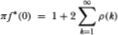
where f* is the normalized spectral density and ρ(k) is the autocorrelation function. Now in order to estimate the quantity πf*(0), the infinite sum on the right-hand side of the preceding equation must obviously be truncated. If, in addition to truncation, the autocorrelations are weighted using Newey and West's (1987) procedure, then the resulting estimator is formally equivalent to our M_r(q)-statistic. Although he does not explicitly use this variance ratio, Huizinga (1987) does employ the Newey and West (1987) estimator of the normalized spectral density.

³Briefly, Hausman (1978) exploits the fact that any asymptotically efficient estimator of a parameter θ, say 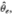must possess the property that it is asymptotically uncorrelated with the difference 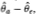, where 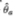is any other estimator of θ. If not, then there exists a linear combination of 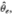and 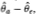that is more efficient than 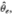contradicting the assumed efficiency of 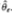. The result follows directly, then, since

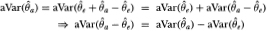
where aVar(·) denotes the asymptotic variance operator.

⁴Note that if (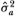)² is used to estimate σ₀⁴, then the standard t-test of J_d = 0 will yield inferences identical to those obtained from the corresponding test of J_r = 0 for the ratio, since

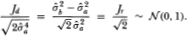
⁵Proofs of all the theorems are given in the Appendices.

⁶According to the results of Monte Carlo experiments in Lo and MacKinlay (1989a), the behavior of the bias-adjusted M-statistics (which we denote as 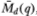and 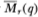does not depart significantly from that of their asymptotic limits even for small sample sizes. Therefore, all our empirical results are based on the M_r(q)-statistic.

⁷See Equation (A.1.6a) in the Appendix.

⁸Note the similarity between these variance ratios and the Box-Pierce Q-statistic, which is a linear combination of squared autocorrelations with all the weights set identically equal to unity. Although we may expect the finite-sample behavior of the variance ratios to be comparable to that of the Q-statistic under the null hypothesis, they can have very diierent power properties under various alternatives. See Lo and MacKinlay (1989a) for further details.

⁹See, for example, Merton (1980), Poterba and Summers (1986), and French, Schwen, and Stambaugh (1987).

¹⁰Of course, second moments are still assumed to finite; otherwise, the variance ratio is no longerwell defined. This rules outdistributionswith infinitevariance, such as those in the stable Parete-Levy family (with characteristic exponents that are less than 2) proposed by Mandelbrot (1963) and Fama (1965). We do, however, allow for many other forms of leptokurtosis, such as that generated by Engle's (1982) autoregressive conditionally heteroskedastic (ARCH) process.

¹¹Condition 2.1.2 is the essential property of the random walk that we wish to test. Conditions 2.1.2 and 2.1.2 are restrictions on the maximum degree of dependence and heterogeneity allowable while still permitting some form of the law of large numbers and the central limit theorem to obtain. See White (1984) for the precised definitions of ø- and α-mixing random sequences. Condition 2.1.2 implies that the sample autocorrelations of ε_t are asymptotically uncorrelated; this condition may be weakened considerably at the expense of computational simplicity (see note 12).

¹²Although this restriction on the fourth cross-moments of ε_t may seem somewhat unintuitive, it is satisfied for any process with independent increments (regardless of heterogeneity) and also for linear Gaussian ARCH processes. This assumption may be relaxed entirely, requiring the estimation of the asymptotic covariances of the autocorrelation estimators in order to estimate the limiting variance θ of 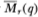via relation (2.1.18). Although the resulting estimator of θ would be more complicated than Equation (2.1.20), it is conceptually straightforward and may readily be formed along the lines of Newey and West (1987). An even more general (and possibly more exact) sampling theory for the variance ratios may be obtained using the results of Dufour (1981) and Dufour and Roy (1985). Again, this would sacrifice much of the simplicity of our asymptotic results.

¹³The average fraction (over all securities) of the entire sample where this occurs is less than 0.5 percent of the time for the 12l6-week sample period.

¹⁴Additional empirical results (304-week subperiods, larger q values, etc.) are reported in Lo and MacKinlay (1987b).

¹⁵Since the values of z*(q) are always smaller than the values of z(q) in our empirical results, to conserve space we report only the more conservative statistics. Both statistics are reported in Lo and MacKinlay (1987b).

¹⁶We also performed our tests using valueweighted portfolios and obtained essentially the same results. The only difference appeared in the largest quintile of the value-weighted portfolio, for which the random walk hypothesis was generally not rejected. This, of course, is not surprising, given that the largest valueweighted quintile is quite similar to the valueweighted market index.

¹⁷See, for example, Scholes and Williams (1977) and Cohen, Hawawini, Maier, Schwartz, and Whitcomb (1983a).

¹⁸Although our model is formulated in discrete time for simplicity, it is in fact slightly more general than the Scholes and Williams (1977) continuowtime model of nontrading. Specifically, Scholes and Williams implicitly assume that each security trades at least once within a given time interval by “ignoring periods over which no trades occur” (page 311), whereas our model requires no such restriction. As a consequence, it may be shown that, ceteris paribus, the magnitude of spuriously induced autocorrelation is lower in Scholes and Williams (1977) than in our framework. However, the qualitative predictions of the two models of nontrading are essentially the same. For example, both models imply that returns for individual securities will exhibit negative serial correlation but that portfolio returns will be positively autocorrelated.

¹⁹Several other factors imply that the actual sizes of the spurious autocorrelations induced by infrequent trading are lower than those given in Table 2.4. For example, in calculating the induced correlations using Equation (2.3.9), we have ignored the idiosyncratic components in returns because diversification makes these components trivial in the limit; in practice, perfect diversification is never achieved. But any residual risk increases the denominator of Equation (2.3.9) and does not necessarily increase the numerator (since the ε_it's are cross sectionally uncorrelated). To see this explicitly, we simulated the returns for 1000 stocks over 5120 days, calculated the weekly autocorrelations for the virtual returns and for the observed returns, computed the diierence of those autocorrelations, repeated this procedure 20 times, and then averaged the differences. With a (daily) nontrading probability of 10 percent, the simulations yield a diierence in weekly autocorrelations of 2.1 percent, of 4.3 percent for a nontrading probability of 20 percent, and of 7.6 percent for a nontrading probability of 30 percent.

Another factor that may reduce the spurious positive autocorrelation empirically is that, within the CRSP files, if a security does not trade, its price is reported as the average of the bid-ask spread. As long as the specialist adjusts the apread to reflect the new information, even if no trade occurs the reported CRSP price will reflect the new information. Although there may still be some delay before the bid-ask spread is adjusted, it is presumably less than the lag between trades.

Also, if it is assumed that the probability of no-trades depends upon whether or not the security has traded recently, it is natural to suppose that the likelihood of a no-trade tomorrow is lower if there is a no-trade today. In this case, it may readily be shown that the induced autocorrelation is even lower than that computed in our IID framework.

²⁰Shillear nd Perron (1985) propose only a mean-reverting process (the Ornstein-Uhlenbeck process), whereas Poterba and Summers (1988) propose the sum of a random walk and a stationary mean-reverting process. Although neither study offers any theoretical justification for its proposal, both studies motivate their alternatives as models of investors’ fads.

²¹If returns are generated by the sum of a random walk and a stationary mean-reverting process, their serial correlation will be a U-shaped function of the holding period; the first-order autocorrelation becomes more negative as shorter holding periods lengthen, but it graudally returns to zero for longer holding periods because the random walk component dominates. The curvature of this U-shaped function depends on the relative variability of the random walk and mean-reverting components. Fama and French's (1988) parameter estimates imply that the autocorrelation coefficient is monotonically decreasing for holding periods up to three years; that is, the minimum of the U-shaped curve occurs at a holding period greater than or equal to three years.

²²This pattern of stronger rejections with larger q is also only uue up to a certain value of q. In view of Fama and French's (1988) results, this upper limit for q is much greater than 16 when the base observation interval is one week. See note 21.

²³See Lo and MacKinlay (1989a) for explicit power calculations against this alternative and against a more empirically relevant model of stock prices.