4
An Econometric Analysis of Nonsynchronous Trading
4.1 Introduction
IT HAS LONG BEEN RECOGNIZED that the sampling of economic time series plays a subtle but critical role in determining their stochastic properties. Perhaps the best example of this is the growing literature on temporal aggregation biases which are created by confusing stock and flow variables. This is the essence of Working’s (1960) now classic result in which time-averages are mistaken for point-sampled data. More generally, econometric problems are bound to arise when we ignore the fact that the statistical behavior of sampled data may be quite different from the behavior of the underlying stochastic process from which the sample was obtained. Yet another manifestation of this general principle is what may be called the “nonsynchronicity” problem, which results from the assumption that multiple time series are sampled simultaneously when in fact the sampling is nonsynchronous. For example the daily prices of financial securities quoted in the Wall Street Journal are usually “closing” prices, prices at which the last transaction in each of those securities occurred on the previous business day. It is apparent that closing prices of distinct securities need not be set simultaneously, yet few empirical studies employing daily data take this into account.
Less apparent is the fact that ignoring this seemingly trivial nonsynchronicity can result in substantially biased inferences for the temporal behavior of asset returns. To see how, suppose that the returns to stocks i and j are temporally independent but i trades less frequently than j. If news affecting the aggregate stock market arrives near the close of the market on one day, it is more likely that j’s end-of-day price will reflect this information than i’s simply because i may not trade after the news arrives. Of course, i will respond to this information eventually but the fact that it responds with a lag induces spurious cross-autocorrelation between the closing prices of i and j. As a result, a portfolio consisting of securities i and j will exhibit serial dependence even though the underlying data-generating process was assumed to be temporally independent. Spurious own-autocorrelation is created in a similar manner. These effects have obvious implications for the recent tests of the random walk and efficient markets hypotheses.
In this chapter we propose a simple stochastic model for this phenomenon, known to financial economists as the “nonsynchronous trading” or “nontrading” problem. Our specification captures the essence of non-trading but is tractable enough to permit explicit calculation of all the relevant time series properties of sampled data. Since most empirical investigations of stock price behavior focus on returns or price changes, we take as primitive the (unobservable) return-generating process of a collection of securities. The nontrading mechanism is modeled as a random censoring of returns where censored observations are cumulated, so that observed returns are the sum of all prior returns that were consecutively censored. For example, consider a sequence of five consecutive days for which returns are censored only on days 3 and 4; the observed return on day 2 is assumed to be the true or “virtual” return, determined by the primitive return-generating process. Observed returns on day 3 and 4 are zero, and the observed return on day 5 is the sum of virtual returns from days 3 to 5.1Each period’s virtual return is random and captures movements caused by information arrival as well as idiosyncratic noise. The particular censoring (and cumulation) process we employ models the lag with which news and noise is incorporated into security prices due to infrequent trading. By allowing cross-sectional differences in the random censoring processes, we are able to capture the effects of nontrading on portfolio returns when only a subset of securities suffers from infrequent trading. Although the dynamics of our stylized model are surprisingly rich, they yield several important empirical implications. Using these results we estimate the probabilities of nontrading to quantify the effects of nonsynchronicity on returns-based inferences, such as the rejection of the random walk hypothesis in Lo and MacKinlay (1988b)).
Perhaps the first to recognize the importance of nonsynchronous price quotes was Fisher (1966)). Since then more explicit models of nontrading have been developed by Scholes and Williams (1977)), Cohen et al. (1978, 1986), and Dimson (1979)). Whereas earlier studies considered the effects of nontrading on empirical applications of the Capital Asset Pricing Model and the Arbitrage Pricing Theory,2 more recent attention has been focused on spurious autocorrelations induced by nonsynchronous trading.3 Our emphasis also lies in the autocorrelation and cross-autocorrelation properties of nonsynchronously sampled data and the model we propose extends and generalizes existing results in several directions. First, previous formulations of nontrading require that each security trades within some fixed time interval whereas in our approach the time between trades is stochastic.4Second, our framework allows us to derive closed-form expressions for the means, variances, and covariances of observed returns as functions of the nontrading process. These expressions yield simple estimators for the probabilities of nontrading. For example we show that the relative likelihood of security i trading more frequently than security j is given by the ratio of the (i, j)th autocovariance with the (j, i)th autocovariance. With this result, specification tests for nonsynchronous trading may be constructed based on the degree of asymmetry in the autocovariance matrix of the returns process. Third, we present results for portfolios of securities grouped by their probabilities of nontrading; in contrast to the spurious autocorrelation induced in individual security returns which is proportional to the square of its expected return, we show that nontrading induced autocorrelation in portfolio returns does not depend on the mean. This implies that the effects of nontrading may not be detectable in the returns of individual securities (since the expected daily return is usually quite small), but will be more pronounced in portfolio returns. Fourth, we quantify the impact of time aggregation on nontrading effects by deriving closed-form expressions for the moments of time-aggregated observed returns. Allowing for random censoring at intervals arbitrarily finer than the finest sampling interval for which we have data lets us uncover aspects of infrequent trading previously invisible to econometric scrutiny. This also yields testable restrictions on the time series properties of coarser-sampled data once a sampling interval has been selected. Finally, we apply these results to daily, weekly, and monthly stock returns to gauge the empirical relevance of nontrading for recent findings of predictability in asset returns.
In Section 4.2 we present our model of nontrading and derive its implications for the time series properties of observed returns. Section 4.3 reports corresponding results for time-aggregated returns and we apply these results in Section 4.4 to daily, weekly, and monthly data. We discuss extensions and generalizations and conclude in Section 4.5.
4.2 A Model of Nonsynchronous Trading
Consider a collection of N securities with unobservable “virtual” continuously-compounded returns Rit at time t, where i = 1,…, N. We assume they are generated by the following stochastic model:
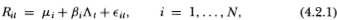
where Λt is some zero-mean common factor and 
it is zero-mean idiosyncratic noise that is temporally and cross-sectionally independent at all leads and lags. Since we wish to focus on nontrading as the sole source of autocorrelation, we also assume that the common factor Λt is independently and identically distributed and is independent of it-k for all i, t, and k.5
In each period t, there is some chance that security i does not trade, say with probability pi. If it does not trade, its observed return for period t is simply 0, although its true or “virtual” return Rit is still given by (4.2.1). In the next period t+1 there is again some chance that security i does not trade, also with probability pi. We assume that whether or not the security traded in period t does not influence the likelihood of its trading in period t+1 or any other future period, hence our nontrading mechanism is independent and identically distributed for each security i.6 If security i does trade in period t+1and did not trade in period t, we assume that its observed return R°it+1 at t+1 is the sum of its virtual returns Rit+1, Rit, and virtual returns for all past consecutive periods in which i has not traded. In fact, the observed return in any period is simply the sum of its virtual returns for all past consecutive periods in which it did not trade. That is, if security i trades at time t + 1, has not traded from time t-k to t, and has traded at time t-k-1, then its observed time t + 1 return is simply equal to the sum of its virtual returns from t-k to t + 1. This captures the essential feature of nontrading as a source of spurious autocorrelation: news affects those stocks that trade more frequently first and influences the returns of thinly traded securities with a lag. In our framework the impact of news on returns is captured by the virtual returns process (4.2.1 ), and the lag induced by thin or nonsynchronous trading is modeled by the observed returns process R°it.
To derive an explicit expression for the observed returns process and to deduce its time series properties we introduce two related stochastic processes:
Definition 4.2.1. Let δit and Xit(k) be the following Bernoulli random variables:
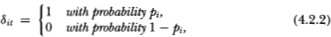
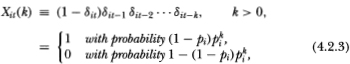
where it has been implicitly assumed that{δit} is an independently and identically distributed random sequence for i = 1, 2,…, N.
The indicator variable δit is unity when security i does not trade at time t and zero otherwise. Xit(k) is also an indicator variable and takes on the value 1 when security i trades at time t but has not traded in any of the k previous periods, and is 0 otherwise. Since pi is within the unit interval, for large k the variable Xit(k) will be 0 with high probability. This is not surprising since it is highly unlikely that security i should trade today but never in the past.
Having defined the Xit(k)’s, it is now a simple matter to derive an expression for observed returns:
Definition 4.2.2. The observed returns process R°it is given by the following stochastic process:
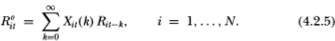
If security i does not trade at time t, then δit = 1 which implies that Xit(k) = 0 for all k, thus R°it = 0. If i does trade at time t, then its observed return is equal to the sum of today’s virtual return Rit and its past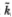 
t virtual returns, where the random variable 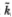t is the number of past consecutive periods that i has not traded. We call this the duration of nontrading and it may be expressed as:
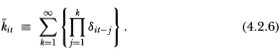
Although Definition 4.2.2 will prove to be more convenient for subsequent calculations, 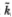it may be used to give a more intuitive definition of the observed returns process:
Definition 4.2.3. The observed returns process R°it is given by the following stochastic process:
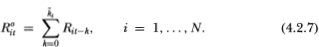
Whereas expression (4.2.5) shows that in the presence of nontrading the observed returns process is a (stochastic) function of all past returns, the equivalent relation (4.2.7) reveals that R°it may also be viewed as a random sum with a random number of terms.7 To see how the probability pi is related to the duration of nontrading, consider the mean and variance of 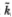it:
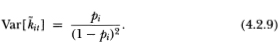
If pi = ½ then security i goes without trading for one period at a time on average; if pi = ¾, then the average number of consecutive periods of nontrading is 3. As expected, if the security trades every period so that pi = 0, both the mean and variance of 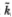it are identically zero.
In Section 4.2.1, we derive the implications of our simple nontrading model for the time series properties of individual security returns and consider corresponding results for portfolio returns in Section 4.2.2.
4.2.1 Implications for Individual Returns
To see how nontrading affects the time series properties of individual returns, we require the moments of R°it which in turn depend on the moments of Xit(k). To conserve space we summarize the results here and relegate their derivation to the appendix:
Proposition 4.2.1. Under Definition 4.2.2 the observed returns processes {R°it} (i = 1,…, N) are covariance-stationary with the following first and second moments:
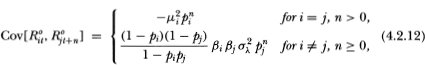
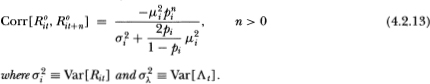
From (4.2.10) and (4.2.11) it is clear that nontrading does not affect the mean of observed returns but does increase their variance if the security has a nonzero expected return. Moreover, (4.2.13) shows that having a nonzero expected return induces negative serial correlation in individual security returns at all leads and lags which decays geometrically. That the autocorrelation vanishes if the security’s mean return μi is zero is an implication of nonsynchronous trading that does not extend to the observed returns of portfolios.
Proposition 4.2.1 also allows us to calculate the maximal negative autocorrelation for individual security returns that is attributable to nontrading. Since the autocorrelation of observed returns (4.2.13) is a nonpositive continuous function of pi, is zero at pi = 0, and approaches zero as pi approaches unity, it must attain a minimum for some pi [0,1). Determining this lower bound is a straightforward exercise in calculus hence we calculate it only for the first-order autocorrelation and leave the higher-order cases to the reader.
Corollary 4.2.1. Under Definition 4.2.2 the minimum first-order autocorrelation of the observed returns process {R°it} with respect to nontrading probabilities pi exists, is given by
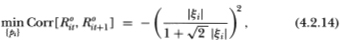
and is attained at
where ξi ≡ μi/σi. Over all values of pi [0, 1) and ξi (-∞, +∞), we have
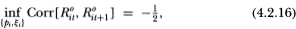
which is the limit of (4.2.14) as |ξi| increases without bound, but is never attained by finite ξi
The maximal negative autocorrelation induced by nontrading is small for individual securities with small mean returns and large return variances. For securities with small mean returns the nontrading probability required to attain (4.2.14) must be very close to unity. Corollary 4.2.1 also implies that nontrading induced autocorrelation is magnified by taking longer sampling intervals since under the hypothesized virtual returns process doubling the holding period doubles μi but only multiplies σi by a factor of √2. Therefore more extreme negative autocorrelations are feasible for longer-horizon individual returns. However, this is not of direct empirical relevance since the effects of time aggregation have been ignored. To see how, observe that the nontrading process of Definition 4.2.1 is not independent of the sampling interval but changes in a nonlinear fashion. For example, if a “period” is taken to be one week, the possibility of daily nontrading and all its concomitant effects on weekly observed returns is eliminated by assumption. A proper comparison of observed returns acro
s distinct sampling intervals must allow for nontrading at the finest time increment, after which the implications for coarser-sampled returns may be developed. We shall postpone further discussion until Section 4.3 where we address this and other issues of time aggregation explicitly.
Other important empirical implications of our nontrading model are captured by (4.2.12) of Proposition 4.2.1. For example, the sign of the cross-autocovariances is determined by the sign of βiβj. Also, the expression is not symmetric with respect to i and j: if security i always trades so that pi = 0, there is still spurious cross-autocovariance between R°it and R°jt+n, whereas this cross-autocovariance vanishes if pj = 0 irrespective of the value of pi. The intuition for this result is simple: when security j exhibits non-trading the returns to a constantly trading security i can forecast j due to the common factor Λt present in both returns. That j exhibits nontrading implies that future observed returns R°jt+n will be a weighted average of all past virtual returns Rjt+n-k (with the Xjt+n(k)’s as random weights), of which one term will be the current virtual return Rjt. Since the contemporaneous virtual returns Rit and Rjt are correlated (because of the common factor), Rit can forecast R°jt+n. The reverse however is not true. If security i exhibits nontrading but security j does not (so that pj = 0), the covariance between R°it and Rjt+n is clearly zero since R°it is a weighted average of past virtual returns Rit-k which is independent of Rjt+n by assumption.8
The asymmetry of (4.2.12) yields an empirically testable restriction on the cross-autocovariances of returns. Since the only source of asymmetry in (4.2.12) is the probability of nontrading, information regarding these probabilities may be extracted from sample moments. Specifically, denote by R°t the vector [R°1t R°2t…R°Nt]′ of observed returns of the N securities and define the autocovariance matrix Γn as
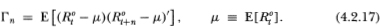
Denoting the (i, j)th element Γn of by γij(n), we have by definition
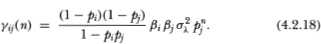
If the nontrading probabilities pi differ across securities, Γn is asymmetric. From (4.2.18) it is evident that:
Therefore relative nontrading probabilities may be estimated directly using sample autocovariances 
n. To derive estimates of the probabilities pi themselves we need only estimate one such probability, say p1, and the remaining probabilities may be obtained from the ratios (4.2.19). A consistent estimator of p1 is readily constructed with sample means and autocovariances via (4.2.12).
4.2.2 Implications for Portfolio Returns
Suppose we group securities by their nontrading probabilities and form equally-weighted portfolios based on this grouping so that portfolio A contains Na securities with identical nontrading probability pa, and similarly for portfolio B. Denote by R°at and R°bt the observed time-t returns on these two portfolios respectively, thus:
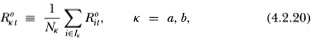
where Ik is the set of indices of securities in portfolio k. Since individual returns are assumed to be continuously-compounded, Rkt is the return to a portfolio whose value is calculated as an unweighted geometric average of the included securities’ prices.9 The time series properties of (4.2.20) may be derived from a simple asymptotic approximation that exploits the crosssectional independence of the disturbances it Since similar asymptotic arguments can be found in the Arbitrage Pricing Theory literature, our assumption of independence may be relaxed to the same extent that it is relaxed in studies of the APT in which portfolios are required to be “well- diversified.”10 In such cases, we have:
Proposition 4.2.2. As the number of securities in portfolios A and B (denoted by Na and Nb, respectively) increases without bound, the following equalities obtain almost surely:
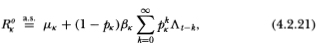
where
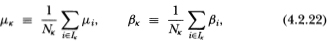
for k = a, b. The first and second moments of the portfolios’ returns are given by
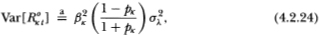
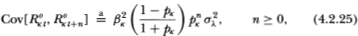
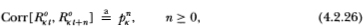
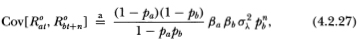
where the symbol “
” indicates that the equality obtains only asymptotically.
From (4.2.23) we see that observed portfolio returns have the same mean as that of its virtual returns. In contrast to observed individual returns, R°at has a lower variance asymptotically than that of its virtual counterpart Rat since:
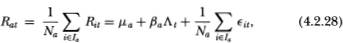
where (4.2.29) follows from the Law of Large Numbers applied to the last term in (4.2.28). Thus 
which is greater than or equal to
Var[R°at].
Since the nontrading-induced autocorrelation (4.2.26) declines geometrically, observed portfolio returns follow a first-order autoregressive process with autoregressive coefficient equal to the nontrading probability. In contrast to expression (4.2.12) for individual securities, the autocorrelations of observed portfolio returns do not depend explicitly on the expected return of the portfolio, yielding a much simpler estimator for pk: the nth root of the nth order autocorrelation coefficient. Therefore, we may easily estimate all nontrading probabilities by using only the sample first-order own- autocorrelation coefficients for the portfolio returns. Comparing (4.2.27) to (4.2.12) shows that the cross-autocovariance between observed portfolio returns takes the same form as that of observed individual returns. If there are differences across portfolios in the nontrading probabilities, the autocovariance matrix for observed portfolio returns will be asymmetric. This may give rise to the types of lead-lag relations empirically documented by Lo and MacKinlay (1990b)) in size-sorted portfolios. Ratios of the cross-autocovariances may be formed to estimate relative nontrading probabilities for portfolios since
Moreover, for purposes of specification testing these ratios give rise to many “over-identifying” restrictions since
for any arbitrary sequence of distinct indices k1,k2,…, kr, a ≠ b, r ≤ Np, where Np is the number of distinct portfolios and 
Therefore, although there are N2p distinct autocovariances in Γn, the restrictions implied by the nontrading process allow only Np(Np +1)/2 of the autocovariances to be arbitrary.
4.3 Time Aggregation
The discrete-time framework we have so far adopted does not require the specification of the calendar length of a “period.” This generality is more apparent than real since any empirical implementation of Propositions 4.2.1 and 4.2.2 must either implicitly or explicitly define a period to be a particular fixed calendar time interval. Once the calendar time interval has been chosen, the stochastic behavior of coarser-sampled data is restricted by the parameters of the most-finely-sampled process. For example, if the length of a period is taken to be one day then the moments of observed monthly returns may be expressed as functions of the parameters of the daily observed returns process. We derive such restrictions in this section. Towards this goal we require the following definition:
Definition 4.3.1. Denote by R°iτ(q) the observed return of security i at time r where one unit of x time is equivalent to q units oft time, thus:
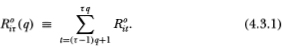
The change of time scale implicit in (4.3.1) captures the essence of time aggregation. We then have the following result:
Proposition 4.3.1. Under the assumptions of Definitions 4.2.1–4.2.3, the observed returns processes {R°iτ(q)} (i = 1,…, N) are covariance-stationary with the following first and second moments:
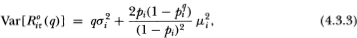
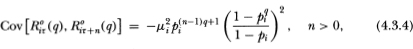
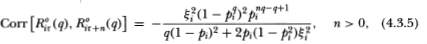
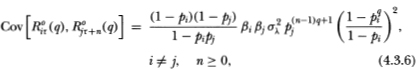
whereξi ≡ μi/σi.
Although expected returns time-aggregate linearly, (4.3.3) shows that variances do not. As a result of the negative serial correlation in R°it, the variance of a sum of these will be less than the sum of the variances. Time aggregation does not affect the sign of the autocorrelations in (4.3.5), although their magnitudes do decline with the aggregation value q. As in
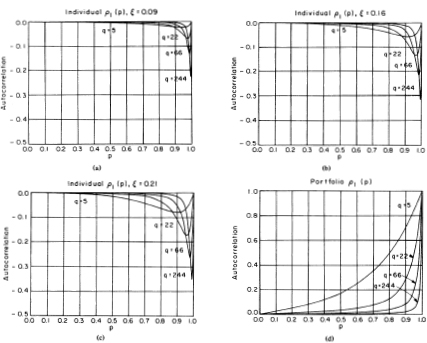
Figure 4.1. First-order autocorrelation of temporally aggregated observed individual and portfolio returns as a function of the per period nontrading probability p, where q is the aggregation value and ξ = μ/σ.
Proposition 4.2.1, the autocorrelation of time-aggregated returns is a non-positive continuous function of pi on [0, 1) which is zero at pi = 0 and approaches zero as pi approaches unity, hence it attains a minimum. To explore the behavior of the first-order autocorrelation, we plot it as a function of pi in Figure 4.1 for a variety of values of q and ξ . As a guide to an empirically plausible range of values for ξ, consider that the ratio of the sample mean to the sample standard deviation for daily, weekly, and monthly equally-weighted stock returns indexes are 0.09, 0.16, and 0.21 respectively for the sample period from 1962 to 1987.11 The values of q are chosen to be 5, 22, 66, and 244 to correspond to weekly, monthly, quarterly, and annual returns since q = 1 is taken to be one day. Figure 4.1a plots the first-order autocorrelation ρ1 (p) for the four values of q with £ =0.09. The curve marked “q = 5” shows that the weekly first-order autocorrelation induced by nontrading never exceeds —5 percent and only attains that value with a daily nontrading probability in excess of 90 percent. Although the autocorrelation of coarser-sampled returns such as monthly or quarterly have more extreme minima, they are attained only at higher nontrading probabilities. Also, time aggregation need not always yield a more negative autocorrelation as is apparent from the portion of the graphs to the left of, say, p = 0.80; in that region, an increase in the aggregation value q leads to an autocorrelation closer to zero. Indeed as q increases without bound the autocorrelation (4.3.5) approaches zero for fixed pi, hence nontrading has little impact on longer-horizon returns. The effects of increasing ξ are traced out in Figures 4.1b and c. Even if we assume ξ = 0.21 for daily data, a most extreme value, the nontrading-induced autocorrelation in weekly returns is at most -8 percent and requires a daily nontrading probability of over 90 percent. From (4.2.8) we see that when pi = 0.90 the average duration of nontrading is 9 days! Since no security listed on the New York or American Stock Exchanges is inactive for two weeks (unless it has been delisted), we infer from Figure 4.1 that the impact of nontrading for individual short-horizon stock returns is negligible.
To see the effects of time aggregation on observed portfolio returns, we define the following:
Definition 4.3.2. Denote by R°aτ (q) the observed return of portfolio A at time r where one unit of x time is equivalent to q units of t time, thus:
where R°at is given by (4.2.20).
Applying the asymptotic approximation of Proposition 4.2.2 then yields:
Proposition 4.3.2. Under the assumptions of Definitions 4.2.1–4.2.3, the observed portfolio returns processes {R°aτ (q)} and {R°bτ(q)} are covariance-stationary with the following first and second moments as Na and Nb increase without bound:
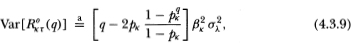
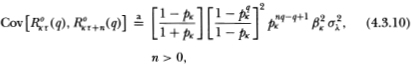
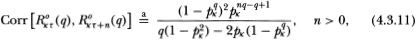
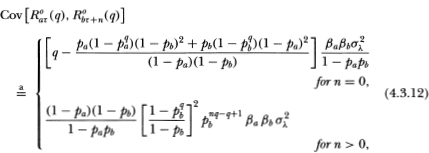
for k = a, b, q > 1, and arbitrary portfolios a, b, and timer τ.
Equation (4.3.11) shows that time aggregation also affects the autocorrelation of observed portfolio returns in a highly nonlinear fashion. In contrast to the autocorrelation for time-aggregated individual securities, (4.3.11) approaches unity for any fixed q as pk approaches unity, hence the maximal autocorrelation is 1.0.12 To investigate the behavior of the portfolio autocorrelation we plot it as a function of the portfolio nontrading probability p in Figure 4.1d for q = 5, 22, 66, and 55. Besides differing in sign, portfolio and individual autocorrelations also differ in absolute magnitude, the former being much larger than the latter for a given nontrading probability. If the nontrading phenomenon is extant, it will be most evident in portfolio returns. Also, portfolio autocorrelations are monotonically decreasing in q so that time aggregation always decreases nontrading induced serial dependence in portfolio returns. This implies that we are most likely to find evidence of nontrading in short-horizon returns. We exploit both these implications in Section 4.4.
4.4 An Empirical Analysis of Nontrading
Before considering the empirical evidence for nontrading effects we summarize the qualitative implications of the previous sections’ propositions and corollaries. Although virtually all of these implications are consistent with earlier models of nonsynchronous trading, the sharp comparative static results are unique to our framework. The presence of nonsynchronous trading:
1. Does not affect the mean of either individual or portfolio returns.
2. Increases the variance of individual security returns (with nonzero mean). The smaller the mean, the smaller is the increase in the variance of observed returns.
3. Decreases the variance of observed portfolio returns when portfolios are well diversified and consist of securities with common nontrading probability.
4. Induces geometrically declining negative serial correlation in individual security returns (with nonzero mean). The smaller the mean (in absolute value), the closer the autocorrelation is to zero.
5. Induces geometrically declining positive serial correlation in observed portfolio returns when portfolios are well-diversified and consist of securities with a common nontrading probability, yielding an AR(1) for the observed returns process.
6. Induces geometrically declining cross-autocorrelation between observed returns of securities i and j which is of the same sign as ßißj. This cross-autocorrelation is asymmetric: the covariance of current observed returns to i with future observed returns to j is generally not the same as the covariance of current observed returns to j with future observed returns to i. This asymmetry is due solely to the assumption that different securities have different probabilities of nontrading.
7. Induces geometrically declining positive cross-autocorrelation between observed returns of portfolios A and B when portfolios are well-diversified and consist of securities with common nontrading probabilities. This cross-autocorrelation is also asymmetric and is due solely to the assumption that securities in different portfolios have different probabilities of nontrading.
8. Induces positive serial dependence in an equally-weighted index if the betas of the securities are generally of the same sign, and if individual returns have small means.
9. And time aggregation increases the maximal nontrading induced negative autocorrelation in observed individual security returns, but this maximal negative autocorrelation is attained at nontrading probabilities increasingly closer to unity as the degree of aggregation increases.
10. And time aggregation decreases the nontrading induced autocorrelation in observed portfolio returns for all nontrading probabilities.
Since the effects of nonsynchronous trading are more apparent in securities grouped by nontrading probabilities than in individual stocks, our empirical application uses the returns of twenty size-sorted portfolios for daily, weekly, and monthly data from 1962 to 1987. We use size to group securities because the relative thinness of the market for any given stock has long been known to be highly correlated with the stock’s total market value, hence stocks with similar market values are likely to have similar non-trading probabilities.13 We choose to form twenty portfolios to maximize the homogeneity of nontrading probabilities within each portfolio while still maintaining reasonable diversification so that the asymptotic approximations of Proposition 4.2.2 might still obtain.14 In Section 4.4.1 we derive estimates of daily nontrading probabilities using daily, weekly, and monthly autocorrelations, and in Section 4.4.2 we consider the impact of nontrading on the autocorrelation of the equally-weighted market index.
4.4.1 Daily Nontrading Probabilities Implicit in Autocorrelations
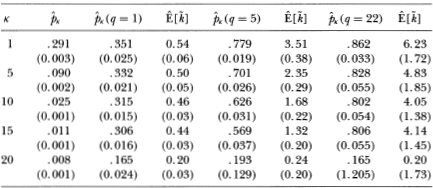
Table 4.1 reports first-order autocorrelation matrices Γ1 for the vector of five of the twenty size-sorted portfolio returns using daily, weekly, and monthly data taken from the Center for Research in Security Prices (CRSP) database. Portfolio 1 contains stocks with the smallest market values and portfolio 20 contains those with the largest.15 From casual inspection it is apparent that these autocorrelation matrices are not symmetric. The second column of matrices are the autocorrelation matrices minus their transposes and it is evident that elements below the diagonal dominate those above it. This confirms the lead-lag pattern reported in Lo and MacKinlay (1990b)). That the returns of large stocks tend to lead those of smaller stocks does support the hypothesis that nonsynchronous trading is a source of correlation. However, the magnitudes of the autocorrelations for weekly and monthly returns imply an implausible level of nontrading. This is most evident in Table 4.2, which reports estimates of daily nontrading probabilities implicit in the weekly and monthly own-autocorrelations of Table 4.1. For example, using (4.3.11) of Proposition 4.3.2 the daily nontrading probability implied by an estimated weekly autocorrelation of 46 percent for portfolio 1 is estimated to be 77.9 percent.16 Using (4.2.8) we estimate the average time between trades to be 3.5 days! The corresponding daily nontrading probability is 86.2 percent using monthly returns implying an average nontrading duration of 6.2 days.
Table 4.1. Sample first-order autocorrelation matrix 1 for the 5×1 subvector [R°0 R°5 R°10 R°15 R°20] of observed returns to twenty equally-weighted size-sorted portfolios using daily, weekly, and monthly stock returns data from the CRSP files for the period 31 December 1962 to 31 December 1987, where portfolios are rebalanced monthly. Only securities with complete daily return histories within each month were included in the daily and monthly returns calculations. R°1 is the return to the portfolio containing securities with the smallest market values and R°20 is the return to the portfolio of securities with the largest. There are approximately equal numbers of securities in each portfolio. The entry in the ith row and jth column is the correlation between R°it and R°jt+1. To gauge the degree of asymmetry in these autocorrelation matrices, the difference 1—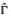'1 is also reported.
For comparison Table 4.2 also reports estimates of the nontrading probabilities using daily data and using trade information from the CRSP files. In the absence of time aggregation, own-autocorrelations of portfolio returns are consistent estimators of nontrading probabilities, hence the entries in the column of Table 4.2 labelled “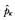
(q = 1)” are simply taken from the diagonal of the autocovariance matrix in Table 4.1. For the smaller securities, the point estimates yield plausible nontrading durations, but the estimated durations decline only marginally for larger-size portfolios. A duration of even only a third of a day is much too large for securities in the second largest portfolio. More direct evidence is provided in the column labelled 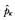which reports the average fraction of securities in a given portfolio that do not trade during the last trading day of the month17. This average is computed over all month-end trading days in 1963 and from 1973 to 1987.The period between 1963 and 1973 is omitted due to trading-status reporting errors uncovered by Foerster and Keim (1989) ). Comparing the entries in this column with those in the others shows the limitations of nontrading as an explanation for the autocorrelations in the data. Nontrading may be responsible for some of the time series properties of stock returns but cannot be the only source of autocorrelation.
Table 4.2. Estimates of daily nontrading probabilities implicit in 20 weekly and monthly size-sorted portfolio return autocorrelations. Entries in the column labelled “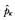” are averages of the fraction of securities in portfolio K that did not trade on the last trading day of the month, where the average is computed over month-end trading days in 1963 and from 1973 to 1987 (the trading-status data from 1964 to 1972 were not used due to errors uncovered by Foerster and Keim (1989))). Entries in the “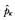(q =1) ”column are the first-order autocorrelation coefficients of daily portfolio returns, which are consistent estimators of daily nontrading probabilities. Entries in the “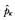(q = 5) ”and “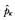(q = 22) ” columns are estimates of daily nontrading probabilities obtained from first-order weekly and monthly portfolio return autocorrelation coefficients, using the time aggregation relations of Section 3 (q = 5 for weekly returns and q = 22 for monthly returns since there are 5 and 22 trading days in a week and a month, respectively). Entries in columns labelled “ 
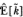” are estimates of the expected number of consecutive days without trading implied by the probability estimates in column to the immediate left. Standard errors are reported in parentheses; all are heteroskedasticity- and autocorrelation-consistent except for those in the second column.
4.4.2 Nontrading and Index Autocorrelations
Denote by R°mt the observed return in period t to an equal-weighted portfolio of all N securities. Its autocovariance and autocorrelation are readily shown to be
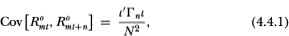
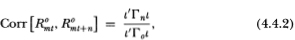
where Γ0 is the contemporaneous covariance matrix of R°t and i is an N×1-vector of ones. If the betas of the securities are generally of the same sign and if the mean returns to each security is small, then R°mt is likely to be positively autocorrelated. Alternatively, if the cross-autocovariances are positive and dominate the negative own-autocovariances the equal-weighted index will exhibit positive serial dependence.
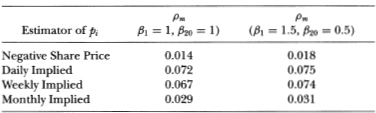
With little loss in generality we let N = 20 and consider the equal- weighted portfolio of the twenty size-sorted portfolios, which is an approximately equal-weighted portfolio of all securities. Using (4.3.6) of Proposition 4.3.1 we may calculate the weekly autocorrelation of R°mt induced by particular daily nontrading probabilities pi and beta coefficients ßi. To do this, we need to select empirically plausible values for pi and ßi, i = 1, 2,…, 20. This is done in Table 4.3 using four different ways of estimating the pi s and two different assumptions for the ßi's. The first row corresponds to weekly autocorrelations computed with the nontrading probabilities obtained from the fractions of negative share prices reported by CRSP. The first entry, 0.014, is the first-order autocorrelation of the weekly equal-weighted index assuming that all twenty portfolio betas are 1.0, and the second entry, 0.018, is computed under the alternative assumption that the betas decline linearly from ß1 = 1.5 for the portfolio of smallest stocks to ß20 = 0.5 for the portfolio of the largest. The next three rows report similar autocorrelations implied by nontrading probabilities estimated from daily, weekly, and monthly autocorrelations using (4.3.11 ).
The largest first-order autocorrelation for the weekly equal-weighted returns index reported in Table 4.3 is only 7.5 percent. Using direct estimates of nontrading via negative share prices yields an autocorrelation of less than 2 percent! These magnitudes are still considerably smaller than the 30 percent autocorrelation reported by Lo and MacKinlay (1988b)). Taken together, the evidence in Sections 4.4.1 and 4.4.2 provide little support for nonsynchronous trading as an important source of spurious correlation in the returns of common stock.
Table 4.3. Estimates of the first-order autocorrelation pm of weekly returns of an equal-weighted portfolio of twenty size-sorted portfolios (which approximates an equal-weighted portfolio of all securities), using four different estimators of daily nontrading probabilities: the average fraction of negative share prices reported by CRSP, and daily nontrading probabilities implied by first-order autocorrelations of daily, weekly, and monthly returns to an equal-weighted index. Since the index autocorrelation depends on the betas of the twenty portfolios it is computed for two sets of betas, one in which all betas are set to 1.0, and another in which the betas decline linearly from ß1 = 1.5 to ß20 = 0.5.
4.5 Extensions and Generalizations
Despite the simplicity of our model of nonsynchronous trading, we hope to have shown the richness of its implications for observed time series. Although its immediate application is to the behavior of asset returns, the stochastic model of random censoring may be of more general relevance to situations involving randomly cumulative measurement errors. Moreover, this framework may be extended and generalized in many directions with little difficulty, and we conclude by discussing some of these here. We mention them only in passing since a more complete analysis is beyond the scope of the present study, but we hope to encourage further research along these lines.
It is a simple matter to relax the assumption that individual virtual returns are independently and identically distributed by allowing the common factor to be autocorrelated and the disturbances to be cross-sectionally correlated. For example, assuming that Λt is a stationary AR(1) is conceptually straightforward although the computations of the Appendix become somewhat more involved. This specification will yield a decomposition of observed autocorrelations into two components: one due to the common factor and another due to nontrading. Allowing cross-sectional dependence in the disturbances also complicates the moment calculations but does not create any intractabilities.18 Indeed, generalizations to multiple factors, time series dependence of the disturbances, and correlation between factors and disturbances are only limited by the patience and perseverance of the reader; the necessary moment calculations are not incalculable, but merely tedious.
We may also build dependence into the nontrading process itself by assuming that the δit's are Markov chains, so that the conditional probability of trading tomorrow depends on whether or not a trade occurs today. Although this specification admits compact and elegant expressions for the moments of the observed returns process space limitations will not permit a complete exposition here. However, a brief summary of its implications for the time series properties of observed returns may suffice: (1) Individual security returns may be positively autocorrelated, portfolio returns may be negatively autocorrelated (but these possibilities are unlikely given empirically relevant parameter values), (2) it is possible (but unlikely) for autocorrelation matrices to be symmetric, and (3) spurious index autocorrelation induced by nontrading is higher (lower) when there is positive (negative) persistence in nontrading. Our initial hope was that property (3) might be sufficient to explain the magnitude of index autocorrelations in recent stock market data. However, several calibration experiments indicate the degree of persistence in nontrading required to yield weekly autocorrelations of 30 percent is empirically implausible.
One final direction for further investigation is the possibility of dependence between the nontrading and virtual returns processes. If virtual returns are taken to be new information then the extent to which traders exploit this information in determining when (and what) to trade will show itself as correlation between Rit and δjt. Many strategic considerations are involved in models of information-based trading, and an empirical analysis of such issues promises to be as challenging as it is exciting. However, if it is indeed the case that autocorrelation in returns is induced by information-based nontrading, in what sense is this autocorrelation spurious? Our premise is that nontrading is a symptom of institutional features such as lagged adjustments and nonsynchronously reported prices, and our empirical results show that this is of little practical relevance. But if nonsynchronicity is purposeful and informationally motivated then the subsequent serial dependence in asset returns may well be considered genuine, since it is the result of economic forces rather than mismeasurement. Although this is beyond the purview of the current framework, it is nevertheless a fascinating avenue for future research and may explain several currently puzzling empirical findings.
Appendix A4
Proof of Propositions
Proof of Proposition 4.2.1
To derive (4.2.10)–(4.2.13), we require the corresponding moments and co- moments of the Bernoulli variables Xit(k). From Definition 4.2.1 it follows that
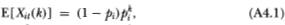
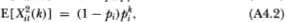
for arbitrary i, t, and k. To compute E[Xit(k) Xit+n(l)], recall from Definition 4.2.1 that
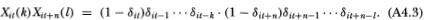
If l ≥ n, then E[Xit(k) Xit+n(l)] = 0 since both δit and 1- δit are included in the product (A4.3), hence the product is zero with probability one. If l < n it may readily be shown that the expectation reduces to (1 - pi)2 pk+1i, hence we have
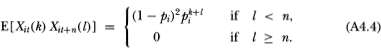
From Definition 4.2.2, we have
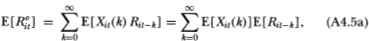
where the second equality in (A4.5a) follows from the mutual independence of Xit(k) and Rit-k. This establishes (4.2.10). To derive (4.2.11) we first obtain an expression for the second uncentered moment of R°it:
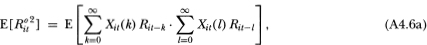
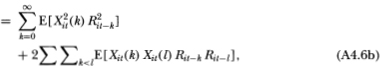
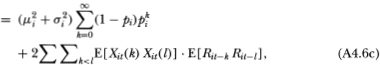
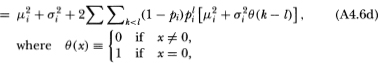
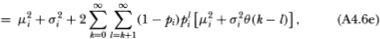
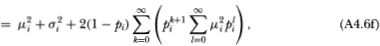
This yields (4.2.11) since
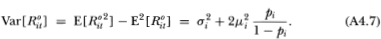
The autocovariance of R°it may be obtained similarly by first calculating the uncentered moment:
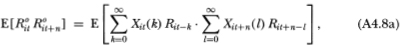
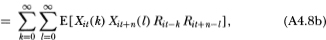
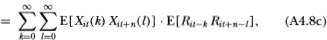
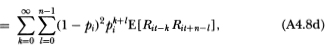
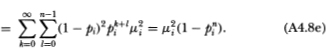
Note that the upper limit of the l-summation in (A4.8d) is finite, which follows from (A4.4). Also, (A4.8e) follows from the fact that {Rit} is an IID sequence and the only combinations of indices k and I that appear in (A4.8d) are those for which Rit-k and Rit+n-l are not contemporaneous, hence the expectation of the product in the summands of (A4.8d) reduces to μ2iin (A4.8e). The autocovariance (4.2.12) then follows since
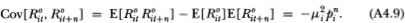
The calculation for the cross-autocovariance between R°it and R°jt+n differs only in that the common factor induces contemporaneous cross-sectional correlation between the virtual returns of securities i and j. Using the fact that
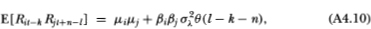
then yields the following:
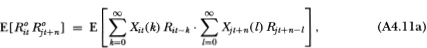
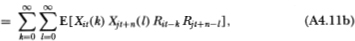
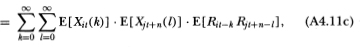
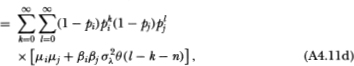
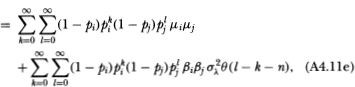
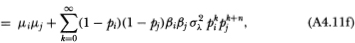
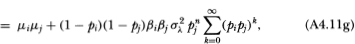
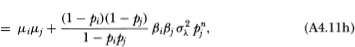
where the cross-sectional independence of the nontrading processes has been used to derive (A4.11c). This yields (4.2.12) since
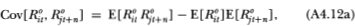
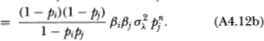
Proof of Proposition 4.2.2
By definition of R°at we have
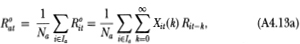
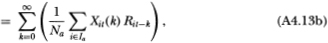
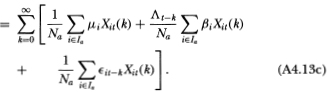
The three terms in (A4.13c) may be simplified by verifying that the summands satisfy the hypotheses of Kolmogorov’s strong law of large numbers, hence:
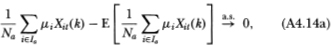
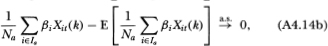
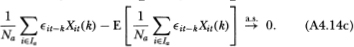
From Definition 4.2.1 we have
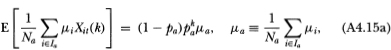
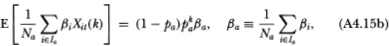
Substituting these expressions into (A4.13c) then yields (4.2.21) :
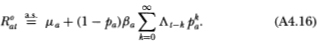
To compute the cross-autocovariance between the two portfolio returns, we use (A4.16):
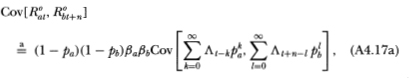
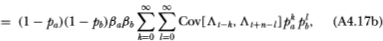
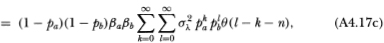
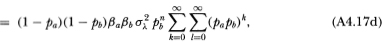
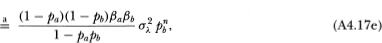
where the symbol indicates that the equality obtains only asymptotically.
Proofs of Propositions 4.3.1 and 4.3.2
Since the proofs consist of computations virtually identical to those of Propositions 4.2.1 and 4.2.2, we leave them to the reader for the sake of brevity.
1Day 1's return obviously depends on how many consecutive days prior to 1 that the security did not trade. If it traded on day 0, then the day 1 return is simply equal to its virtual return; if it did not trade at 0 but did trade at -1, then day 1's return is the sum of day 0 and day 1's virtual returns; etc.
2See, for example, Cohen et al. (1983a,b), Dimson (1979)), Scholes and Williams (1977)), and Shanken (1987a)).
3See Atchison, Butler, and Simonds (1987)), Cohen et al. (1979,1986), Lo and MacKinlay (1988b)), and Muthuswamy (1988)).
4For example, Scholes and Williams (1977, fn. 4) assume: “All information about returns over days in which no trades occur is ignored.” This is equivalent to forcing the security to trade at least once within the day. Muthuswamy (1988) ) imposes a similar requirement. Assumption A1 of Cohen et al. (1986, ch. 6.1) requires that each security trades at least once in the last N periods, where N is fixed and exogenous.
5These strong assumptions are made primarily for expositional convenience and may be relaxed considerably. See Section 4.5 for further discussion.
6This assumption may be relaxed to allow for state-dependent probabilities, i.e., autocorrelated nontrading; see the discussion in Section 4.5.
7This is similar in spirit to the Scholes and Williams (1977)) subordinated stochastic process representation of observed returns, although we do not restrict the trading times to take values in a fixed finite interval. With suitable normalizations it may be shown that our nontrading model converges weakly to the continuous-time Poisson process of Scholes and Williams (1976)). From (4.2.5) the observed returns process may also be considered an infinite-order moving average of virtual returns where the MA coefficients are stochastic. This is in contrast to Cohen et al. (1986, ch. 6) in which observed returns are assumed to be a finite-order MA process with nonstochastic coefficients. Although our nontrading process is more general, their observed returns process includes a bid-ask spread component; ours does not.
8An alternative interpretation of this asymmetry may be found in the causality literature, which R°it is said to “cause” R°jt if the return to i predicts the return to j. In the above example, security i “causes” security j when j is subject to nontrading but i is not. Since our nontrading process may be viewed as a form of measurement error, the fact that the returns one security may be “exogenous” with respect to the returns of another has been proposed under a different guise in Sims (1974,1977).
9The expected return of such a portfolio will be lower than that of an equally-weighted portfolio whose returns are calculated as the arithmetic means of the simple returns of the included securities. This issue is examined in greater detail by Modest and Sundaresan (1983)) and Eytan and Harpaz (1986)) in the context of the Value Line Index which until recently was an unweighted geometric average.
10See, for example, Chamberlain (1983)), Chamberlain and Rothschild (1983)), and Wang (1988) ). The essence of these weaker conditions is simply to allow a Law of Large Numbers to be applied to the average of the disturbances, so that “idiosyncratic risk” vanishes almost surely as the cross-section grows.
11These are obtained from Lo and MacKinlay (198813, Tables la, b, c).
12Muthuswamy (1988)) reports a maximal portfolio autocorrelation of only 50 percent because of his assumption that each stock trades at least once every T periods, where T is some fixed number.
13This is confirmed by the entries of Table 4.3's second column and by Foerster and Keim (1989)).
14The returns to these portfolios are continuously-compounded returns of individual simple returns arithmetically averaged. We have repeated the correlation analysis for continuously compounded returns of portfolios whose values are calculated as unweighted geometric averages of included securities' prices. The results for these portfolio returns are practically identical to those for the continuously-compounded returns of equally-weighted portfolios.
15We report only a subset of five portfolios for the sake of brevity; the complete set of autocorrelations may be obtained from the authors on request.
16Standard errors for autocorrelation-based probability and nontrading duration estimates are obtained by applying the “delta” method to (4.2.8) and (4.3.11) using heteroskedasticity and autocorrelation-consistent standard errors for daily, weekly, and monthly first-order autocorrelation coefficients. These latter standard errors are computed by regressing returns on a constant and lagged returns, and using Newey and West's (1987) procedure to calculate heteroskedasticity- and autocorrelation consistent standard errors for the slope coefficient (which is simply the first-order autocorrelation coefficient of returns).
17This information is provided in the CRSP daily files in which the closing price of a security is reported to be the negative of the average of the bid and ask prices on days when that security did not trade. See Foerster and Keim (1989)) for a more detailed account. Standard errors for probability estimates based on the fraction of no-trades reported by CRSP are derived under the assumption of a temporally IID nontrading process {δit} ; the usual binomial approximation yields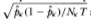 
as the standard error for the estimate 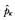, where Nk is the number of securities in portfolio K and T is the number of daily observations with which the nontrading probability pk is estimated. For our sample and portfolios, Nk T fluctuates about 20,000 (192 daily observations, 105 securities per portfolio on average).
18As we discussed earlier, some form of cross-sectional weak dependence must be imposed so that the asymptotic arguments of the portfolio results still obtain. Of course, such an assumption may not always be appropriate as, for example, in the case of companies within the same industry, whose residual risks we might expect to be positively correlated. Therefore, the asymptotic approximation will be most accurate for well-diversified portfolios.