11

Index-Futures Arbitrage and the
Behavior of Stock Index Futures Prices

THE SPECTACULAR GROWTH in the volume of trading in stock index futures contracts reveals the interest in these instruments that is shared by a broad cross section of market participants. It is generally agreed that the linkage in prices between the underlying basket of stocks and the futures is maintained by arbitrageurs. If this link is maintained effectively, then investors who are committed to trade will recognize these markets as perfect substitutes, and their choice between these markets will be dictated by convenience and their transaction costs. However, researchers have reported substantial and sustained deviation in futures prices from their theoretical values; indeed, Rubinstein (1987, p. 84) concludes that “The growth in index futures trading continues to outstrip the amounts of capital that are available for arbitrage.”

Considerable attention has been focused on arbitrage strategies involving stock index futures and on their effects on markets, especially on the expiration dates of these contracts. By contrast, there is little work on the stochastic behavior of the deviation of futures prices from fair values. In this chapter, we study transaction data on Standard & Poor's 500 futures contracts in conjunction with minute-by-minute quotes of the S&P 500 index. Our goal is to examine the behavior of these prices in light of the conventional arbitrageur's strategies.

It should be emphasized at the outset that it is extremely difficult to specify a model for the deviations of futures prices from “fair values.” These deviations are, presumably, affected by the flow of orders as well as by the difference of opinion among participants regarding parameters of the valuation model that provides “fair values.” It is well known that the conventional strategies pursued by arbitrageurs to take advantage of these deviations are not risk-free, and are influenced further by the transaction costs they involve. The purpose of this chapter is to examine the empirical behavior of these deviations; in doing so, we examine the validity of certain proposed hypotheses regarding the stochastic behavior of these deviations, given that market participants will attempt to exploit these as profit opportunities.

In Section 11.1 we discuss some considerations of the behavior of futures and index prices after describing the well-known and commonly used pricing model. Section 11.2 provides the empirical results, and we conclude in Section 11.3.

11.1 Arbitrage Strategies and the Behavior of
Stock Index Futures Prices

The arguments underlying the valuation of derivative assets exploit the availability of a replicating portfolio of existing assets whose value coincides with the price of the derivative security at its expiration date. In frictionless markets the availability of a perfect substitute for the derivative asset guarantees that a profit opportunity, if one surfaced, would attract “arbitrageurs” who would quickly close the gap between the price of the asset and of its substitute. The presence of transaction costs implies that the price of the derivative asset could fluctuate within a band around its theoretical value without representing a potential profit opportunity. The width of this band would be dictated by the transaction costs of the most favorably situated arbitrageurs. In the context of the daily settlement prices of stock index futures contracts, this has been examined by Modest and Sundaresan (1983). However, the band could also be affected by the fact that the replicating portfolio of existing assets serves only as a close substitute, and that the temporal behavior of the spread between the market price and a model value is further influenced by alternative trading strategies that will be employed by arbitrageurs. We examine these issues in this section.

It is well known, from the work of Black and Scholes (1973), that the replicating portfolio for an option involves a dynamic, self-financing trading rule that depends on the unobservable volatility parameters for the stochastic process of the underlying asset's price. However, for a forward contract, the replicating portfolio involves a buy-and-hold strategy that, in the absence of random payouts from the underlying asset, depends only on observable quantities. The differences between forward prices and futures prices have been studied extensively (see, for example, Black (1976); Cox, Ingersoll, and Ross (1981); Richard and Sundaresan (1981); Jarrow and Oldfield (1981); and French (1983)). With nonstochastic interest rates, forward and futures prices will be equal; however, the replicating portfolio for futures contracts will involve a dynamic trading rule even in this case.¹ In practice, it is generally argued that differences in forward and futures prices are small enough to be safely ignored; indeed, many programs that seek to arbitrage the price differences by trading in stock index futures and in the basket of stocks representing the index employ the forward pricing model adjusted for transaction costs. We begin by briefly examining this model for forward prices on stock index portfolios (with and without transaction costs), and we draw implications for the behavior of futures prices over a contract's life.

11.1.1 Forward Contracts on Stock Indexes (No Transaction Costs)

Consider a forward contract on an index of stocks, where the index represents a capitalization-weighted basket of stocks and is a feasible buy-and-hold portfolio. Assume that markets are perfect and frictionless, that any performance bonds necessary to take a position in the forward market can be posted in interest-bearing assets, that borrowing and lending take place at the (constant) continuously compounded rate r, and that the basket of stocks representing the index pays dividends continuously at the rate d. Consider the following portfolio, constructed at date t and held until the forward contract expires at date T:

1. Buy the basket of stocks at the price S_t (the index price at date t) and continuously reinvest the dividends received until date T.
2. Borrow $S_t at t to finance the acquisition in Equation (11.1.1).
3. Sell a forward contract at the currently quoted forward price G_t,T.

This portfolio is costless at t; and to avoid certain losses or gains at T, it can be shown that

If the forward price at market 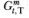is greater than 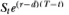, then a strategy that buys the index and sells forward contracts will earn riskless profits in excess of the risk-free rate r. If 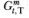is less, then a strategy that sells the index and buys futures contracts will achieve a financing rate below the risk-free rate.²

11.1.2 The Impact of Transaction Costs

Stoll and Whaley (1986) discuss the impact of transaction costs on the index-futures arbitrage strategy, starting with the forward-contract pricing relation shown above. The impact of transaction costs is to permit the futures price to fluctuate within a band around the formula value in relation (11.1.1). The width of the band derives from round-trip commissions in the stock and futures markets and from the market impact costs of putting on the trade initially. The market impact costs of closing the stock position can be avoided by holding the position until expiration of the futures contract and employing market-on-close orders.³

We consider two issues related to this view. First, this line of argument says that the mispricing around the formula value (the band) should not exceed a value (dictated by transaction costs) that is constant over the life of the contract. That is, if the transaction costs are independent of the remaining maturity for the contract, then the width of the band should not vary over time.⁴ Second, this argument provides no role for the arbitrageurs when futures prices lie within the band; there is no influence on the trajectory of the futures price as long as it does not stray from its transaction-cost-based limits. Consider the commonly defined “mispricing,”⁵

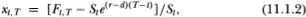
which is the difference between the market futures price of the stock index futures contract (F_t,T) and its theoretical price (assuming that it is a forward contract), all normalized by the index value.⁶ The transaction-cost limits for x_{t, T} would be given by the sum of the commission costs in the stock and futures markets, plus the market impact cost of trading initially in the stocks and in the futures. Sustained deviations of x_{t, T} outside these limits would be evidence of the lack of arbitrage capital. This view implies that x_{t, T} should be clipped above and below at these limits but provides no guidance with respect to its behavior within the boundaries.

We argue that larger deviations in x_{t, T} can persist outside these transaction-cost (TC) limits for longer times until expiration (T – t). This may occur for several reasons. First, with longer times until expiration, there is increased risk of unanticipated increases or decreases in dividends. These will erode the anticipated profits from an attempt to arbitrage x_{t, T} when it violates these limits. Put another way, programs that seek riskless profits should account for worst-case dividend policies. Second, the difference between futures and forward prices, which is embedded in the definition in Equation (11.1.2), reflects the unanticipated interest earnings or costs from financing the marking-to-market flows from the futures position. An attempt to replicate the futures-contract payoff will require trading in the stocks, and both of these will contribute to a wider limit for x_{t, T} with greater times to expiration. Finally, attempts at arbitrage-motivated trading that employ less than the full basket of stocks in the index must allow for a greater margin of error with longer times to expiration. This would arise not only because of the possibility that the value of the chosen basket might not track the index accurately, but also because costly adjustments would be necessary prior to expiration. Consequently, wider deviations in x_{t, T} will be required at longer times to maturity in order to induce arbitrageurs to take a position in these markets. These considerations point up the fact that the “arbitrage” strategies are not risk-free.

There are countervailing forces that serve to provide a narrower trading band, and they stem from the fact that arbitrageurs have the option either to reverse their positions prior to the expiration date or to roll forward their futures position into the next available maturity.⁷ To see this, suppose that an arbitrageur views the random mispricing x_t.T as an arbitrageable sequence whose current level is observable. She knows that the mispricing disappears at date T so that x_T,T = 0. The arbitrage strategy conventionally considered is to sell x_t,T if it is positive at date t and to reverse the position at T, or to buy it if x_{t, T} is negative and to reverse that position at date T, as long as

where more TC₁ = round-trip stock commission + round-trip futures commission + market impact in futures + market impact in stocks.⁸ However, the arbitrageur knows that at a future date s < T it is possible for her (a) to reverse her position by paying a market impact cost in both the stock and futures markets or (b) to roll her futures position into the next maturity and incur commissions and market impact costs only in the futures market. Therefore, the optimal band at which to undertake an opening position would be narrower than the optimal band in the absence of strategies (a) and (b). This is because at the current date t, with an arbitrage program trade already in place, the arbitrageur benefits from the option value of closing her position prematurely at perhaps a greater profit than indicated by the current level x_{t, T.} Given these two arguments, it is important to examine empirically the behavior of the deviations as a function of time to maturity. We consider this in the next section.

However, this option argument has a further implication. Once an arbitrage trade has been put on, it will be optimal to close that position prior to putting on a new arbitrage program in the reverse direction. Suppose that we had put on an arbitrage at date t (in the past) when x_{t, T.} > 0 by buying the index basket and selling futures short. Then, to initiate an offsetting trade at the current date, we would incur additional costs TC₂, where TC₂ is simply the sum of the market impact costs in the stock and futures markets. If we were to undertake this as a net new position, we would need to cover the higher costs TC₁. The implication is that the stochastic behavior of the mispricing will display properties, over the next interval, that depend on the history of the mispricing until that point. Suppose that the historical trajectory of the mispricing x_{t, T.} has been positive and large. Then arbitrageurs who had undertaken positions long in index stocks and short in futures will undo them when at date s > T the mispricing x_s,T. has fallen to some negative value. The magnitude of this value will depend, among other things, on the additional transaction costs from closing the position prematurely (TC₂). If the mispricing never “corrects” itself over the life of the contract, then the burden of the reversing trades will fall at the close of the expiration date. In fact, the direction of market-on-close (or, since the June 1987 expiration, market-on-open) orders on expiration days may be predictable only if the history of the mispricing indicates that the arbitrageurs took positions that were all on one side of the market and did not have the opportunity to reverse or roll forward these positions profitably. In Section 11.2 we consider the hypothesis that the behavior of x_{t, T.} over time displays non-Markov properties: its distribution over the future is dependent on its path in the past.

11.2 Empirical Evidence

In this section we present evidence using the intraday prices for the Standard & Poor's 500 futures contract and for the underlying index. This evidence deals with the behavior of the futures and index prices and with the hypotheses regarding the behavior of the mispricing series x_t,T. WE begin first by describing the data employed.

11.2.1 Data

The futures-price database, obtained from the Chicago Mercantile Exchange, consists of time-stamped transaction data for transactions in the S&P 500 futures contracts from April 1982 (the inception of trading) to June 1987. The contracts traded follow the March-June-September-December cycle—although the nearest contract is typically the most heavily traded. Each transaction record contains (in addition to contract identification, time stamp, and price) information which tags that transaction as a sale, a bid, or an offer and which indicates whether it was canceled, corrected, or a designated open or a close. The size (number of contracts) of the transaction is not available.

These transaction data record only transactions with price changes. Because the trading occurs by open outcry in a continuous market, the time stamping of a consummated transaction will lag by a few seconds, and perhaps by more in periods of heavy trading. In these periods particularly, it is possible to have the records stamped out of sequence. We observed several transactions subsequent to 9:00 A.M. (subsequent to 8:30 A.M. after October 1,1985) occurring before the transaction that was labeled as the open—this signified the end of the opening “round” of transactions. Likewise, we observed transactions after the first designated closing “round” of transactions, occurring after 3:14 P.M. Almost always, these open- and close-designated records are also marked as representing a sale (as opposed to a bid or an offer).

The database of S&P 500 stock index quotes, time-stamped approximately one minute apart, was also provided to us by the Chicago Mercantile Exchange (CME). The index is updated continuously using transaction prices (the most recent prices as reported) of the component 500 stocks. This database captures these quotations approximately 60 seconds apart. While traders on the floor of the CME have access to continuously updated series, the index series available contains stale prices, especially for the thinly traded stocks; and the quoted index fails to use the bid or offer side of the market, so that the price at which one can buy or sell the index basket might be higher or lower than the quoted value. These facts must be kept in mind when working with the mispricing series.

In computing the mispricing series, we use quotes that are approximately 15 minutes apart, and we employ the nearest quotes available after the quarter-hour mark. Each contract is followed from the expiration date of the previous contract until its expiration. Because the near futures are heavily traded, and our stock index quotes are clocked one minute apart, this means that our futures price will be stamped almost immediately following the quarter-hour mark, while the index quote will be, on average, 30 seconds after the quarter-hour mark. The mispricing computed from these quotes will be biased, perhaps slightly, in favor of signaling potential profit opportunities. Conversations with market makers suggest that the time taken to put on a simultaneous program in the stock and futures markets depends, among other things, on the size of the trade, on the composition of the stock basket, and on the depth of the market—the estimates range from 60 seconds to several minutes⁹ Usually, the futures leg can be executed very quickly. This means that, because we do not compute a separate series that would represent executable profits after recognizing a profit opportunity, the constructed series may be inappropriate to judge the actual profitability of program trades.

In order to construct the mispricing series x_{t, T.}, we require dividend forecasts for the 500 stocks in the index, and a measure of the interest rate for loans maturing at the expiration date of the futures. We use the realized daily dividend yield of the value-weighted index of all NYSE stocks supplied by the Center for Research in Security Prices (CRSP) at the university of Chicago as a proxy for the yield of the S&P 500.¹⁰ Given that the S&P 500 is also value-weighted, the CRSP value-weighted dividend yield should be a reasonably proxy. Furthermore, given that the average maturity of our futures contracts is 1½ months, the error in employing this series is likely to be small. The daily interest data for Treasury bills and for certificates of deposit expiring around the expiration date were kindly supplied by Kidder, Peabody. Throughout this chapter we report results using the rates for certificates of deposit; results using the Treasury-bill interest rate were also calculated and are similar to those with the CDs.

The mispricing series so constructed is available for every quarter-hour mark until 4:00 P.M. EST, although the S&P 500 futures contracts continue to trade until 4:15 P.M. This series is constructed starting with the September 1983 contract; we avoided using earlier contracts because prior studies had reported unusual behavior for these.¹¹ In Section 11.2.2 we report on the behavior of the futures and index series used to construct the mispricing. Section 11.2.3 considers the behavior of the actual mispricing series.

11.2.2 Behavior of Futures and Index Series

In this section we examine the behavior of futures prices and index prices for each of the 16 contracts from September 1983 through June 1987. We present evidence on the autocorrelations and on the variability of futures prices and index prices; our focus is on (1) the extent to which nonsynchronous (or state) prices are a problem in available index values and (2) the relative variability of the prices in two markets.¹²

The results reported in this section employ first differences in the logarithm of the futures price and in the logarithm of the index value over the appropriate interval. By varying the interval length (we use 15, 30, 60, and 120 minutes and one trading day), we can assess the importance of stale prices in the index quotes.

Table 11.1 reports the autocorrelation estimates at eight lags for the price changes for both the futures- and the spot-price series using the 15- minute interval. They are computed from intraday intervals only: overnight and weekend intervals are discarded. The autocorrelations of the futures series are close to 0.0 at all eight lags, with only a slight tendency for the first-order autocorrelation coefficient to be negative; it is likely that this is induced by the observed futures prices bouncing between the bid and asked prices. By contrast, the index series is positively autocorrelated at the first lag, with first-order autocorrelations ranging from 0.038 to 0.41 across the 16 contracts. At lags beyond the first, the index series exhibits autocorrelations close to zero. These results are consistent with the presence of stale prices in the available index quotes. It is noteworthy that the problem of stale prices has diminished over time: the first-order autocorrelations for the index series are noticeably smaller in the recent past. This finding may be attributed to increased stock market trading volume in recent years.

The autocorrelations for longer differencing intervals (except for one trading day) are based on estimates that exploit the overlapping nature of the data: these estimators are formed as a function of the estimators for 15-minute intervals. For example, the first-order autocorrelation for the 60-minute differencing interval, ρ₆₀(l),is given by¹³

where ρ(j) = jth-order correlation for 15-minute intervals. Given that our basic series uses 15-minute intervals, this estimator is efficient in exploiting the degree of overlap. We do not report higher-order autocorrelations for the longer differencing intervals.

Table 11.1. Autocorrelations for changes of the logarithm of price in the S&P 500 futures and index by contract, September 1983 to june 1987.

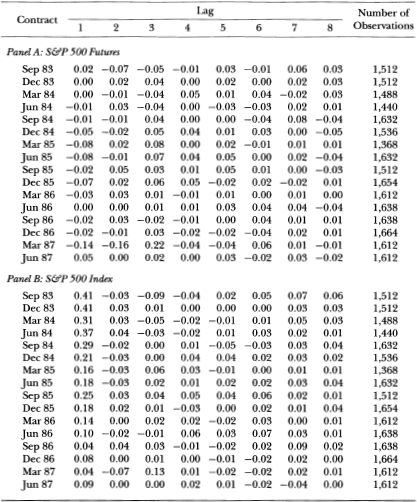
Autocorrelations are based on 15-minute observation intervals.

 

Panels B, C, D, and E of Table 11.2 present the first-order autocorrelations for the longer differencing intervals of 30, 60, and 120 minutes and one trading day, respectively. Two results emerge from these panels. First, the problem of nonsynchronous data in the index series is mitigated by employing longer differencing intervals: At 30 minutes, the first-order autocorrelation in the index series (panel B) is much smaller than the first-order autocorrelation at 15 minutes (panel A), and the corresponding value at 60 minutes (panel C) is close to zero. Second, whenever the first-order autocorrelation for the index series is high (for any contract, over the longer differencing intervals), the autocorrelation for the futures series also tends to be high. For example, the 120-minute-interval data in panel C provides evidence that, for the September 1984 contract, the index series' autocorrelation was 0.19, but the futures autocorrelation was also high at 0.17. This indicates that nonsynchronous data are not the sole source of autocorrelation.

We turn now to the variability of the two data series. If arbitrageurs maintained the link between these markets, then the variability of the two series should be equal: this is in keeping with the “redundant security” view, and it is consistent with the implication from a forward pricing model, as long as interest rates and dividends are nonstochastic. Furthermore, if differences in transaction costs are large between these two markets, it is possible that new information is incorporated with greater speed in one market relative to the other. Therefore, these differences would exhibit themselves when we examine the variability of the two series, especially for the smaller differencing intervals.

Panels A through E of Table 11.2 report the standard deviations for the two series for the five observation intervals. Panel A reports the standard deviation for the basic 15-minute differencing interval as well as the variance ratio for the futures and index series. The standard deviations of the futures series are all higher than those for the index, but this might be due solely to nonsynchronous prices rather than to a structural feature of the markets. The results for longer intervals, in panels B through E, serve to resolve this issue.¹⁴

If the variability of the two markets is equal, then as the observation interval is lengthened and the stale-price problem is mitigated, the variance ratio of the futures series to the index series should approach 1. However, this is not the case. The ratio in most cases is above 1 for all intervals. Table 11.3. reports some aggregated evidence of the higher variability of the futures market. The average variance ratio for the 16 contracts is presented for each interval length. The average drops considerably from the 15-minuteinterval average of 1.56 to the 60-minute-interval average of 1.16 but remains flat from the 60-minute interval to the one-trading-day interval. We test the hypothesis that the ratio equals 1 by treating the ratios as being independent across contracts. The z-statistics for this test are reported in Table 11.3. The smallest z-statistic is 4.40 for the 120-minute interval, supporting the hypothesis that the futures market is more variable than the spot market.

Table 11.2. Summary statistics for the changes of the logarithm of price in the S&P 500 futures and index by contract, September 1983 to June 1987.

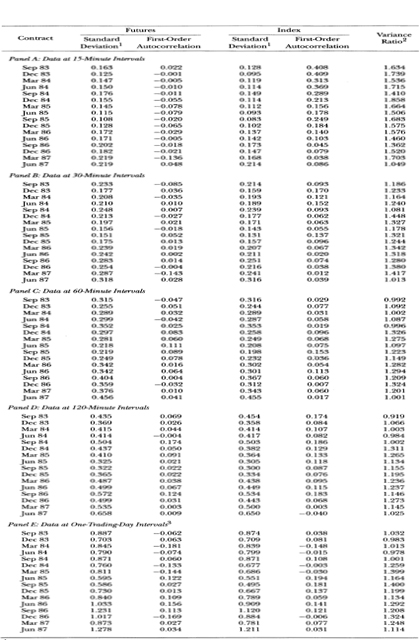
¹The standard deviation is reported in percent.

²The variance ratio is the variance of the change of log futures price divided by the variance of the change of log index price.

³Results are calculated using prices at 3 p.m. EST.

Table 11.3. Aggregate variance-ratio results (based on 16 contracts, September 1983 to june 1987).

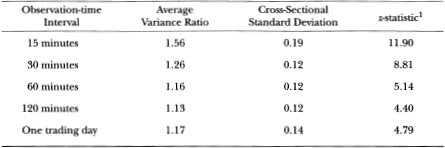
¹The null hypothesis is that the average variance ratio equals 1.

11.2.3 The Behavior of the Mispricing Series

We now examine the behavior of the mispricing series. Data for two contracts, December 1984 and March 1987 (employing data 15 minutes apart), are plotted in Figure 11.1. The graphs display some sharp reversals in the mispricing levels, but the tendency is for the series to stay above or below zero for substantial lengths of time. A single sharp spike that penetrates a transactions bound (placed, say, at ±0.6 percent) is more likely to be symptomatic of a lagging and smoothed index than an arbitrage opportunity. The 100-point-scale interval on the x-axis corresponds to 1500 minutes, or approximately four trading days. These graphs provide a visual description of the typical behavior of the mispricing series.

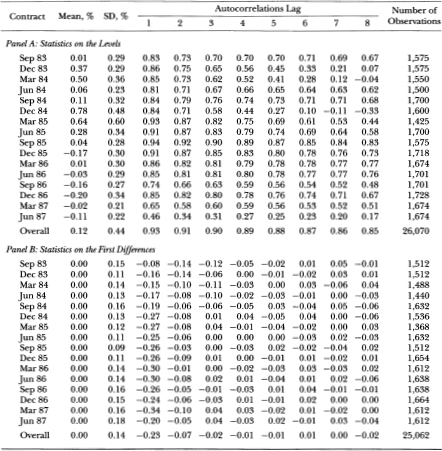
Table 11.4 reports the means, standard deviations (SDs), and autocorrelations at eight lags for the levels and the first differences in the constructed mispricing series. We report the results for the overall time period, June 1983 through June 1987, as well as for the 16 separate contracts. All statistics are computed using the quarter-hour intervals: overnight and weekend intervals are treated as missing observations and are not included in the computations.

The results for the mispricing levels are in panel A of Table 11.4. Over the 16 contracts, the average mispricing is 0.12 percent. For the December 1986 contract, the average mispricing is the lowest, with a mean of –0.20 percent; it is the highest for the December 1984 contract (0.78 percent). These results are consistent with the hypothesis that the forward pricing model gives a downward-biased estimate for the futures price, but the short time period and the small number of contracts considered prohibit one from drawing strong conclusions. The overall standard deviation of the mispricing levels is 0.44 percent. Panel B of Table 11.4 reports the corresponding results for the first differences in the mispricing series (the “changes”). The mean of these changes is 0.00 percent for all the contracts—as one might expect, given that the level of the mispricing is constrained by arbitrageurs. The standard deviations are fairly stable across all contracts, that for the overall period being 0.14 percent.

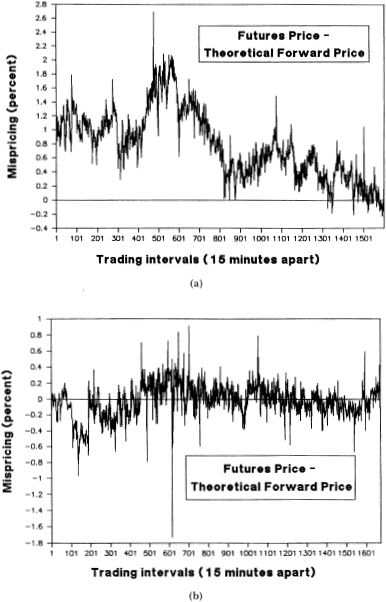
Figure 11.1.  Mispricing (percent of index value) for (a) December 1984 and (b) March 1987 S&P 500 futures contracts.

Table 11.4.  Summary statistics on the levels and first differences in mispricing in the S&P 500 futures contracts, by expiration ( 15-minute-interval transaction data, mispricing in percent of index value).

Mispricing = futures price - theoretical forward price.

 

The series of the mispricing levels is highly autocorrelated (Table 11.4, panel A). For the individual contracts, the first-order autocorrelation coefficient ranges from 0.46 to 0.94. For 12 of the 16 contracts, the autocorrelation is quite high for all eight lags reported (a two-hour time interval). This indicates that the series tends to persist above or below zero and not, as one might have conjectured, fluctuate randomly around zero.¹⁵ The autocorrelation behavior of the first differences in the mispricing are close to zero, except for the first two lags for which they are all negative (Table 11.4, panel B). The first-order autocorrelation ranges from –0.34 to –0.08; the second-order autocorrelations are smaller in magnitude and range from –0.14 to –0.01. The negative autocorrelations at low lags are consistent with the implication that when the mispricing deviates from zero it is elastically pulled toward zero by the action of those traders who perceive that transacting in one market is cheaper.¹⁶

We also examine the relation between the magnitude of the mispricing and the contract's maturity. Because we lack the theoretical framework to suggest a precise functional form, we simply estimate a linear relation between the average absolute mispricing at 15-minute intervals over a given day and the number of days remaining until maturity. The model we estimate is

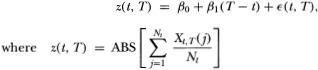
x_{t, T}(j) = mispricing at the jth quarter-hour mark during day t, for futures contract maturing at T;

      N_t = number of observations in day t.

The results indicate that the magnitude of the mispricing is positively related to time until maturity. For the overall time period, the estimates of β₀ and β₁ are 0.014 percent and 4.41, respectively. The z-statistic for the null hypothesis of β₁ = 0 is 3.83.¹⁷,¹⁸ Figure 11.2 is drawn using these estimates from the overall relationship, and it illustrates the cone-shaped boundary that one obtains for the mean mispricing as a function of time until maturity. If these boundaries are strictly determined by round-trip transaction costs alone, then a flat corridor should result. The results indicate that the bounds drawn (as estimated) in Figure 11.2 are consistent with the impact of other factors that are influenced by time to expiration, such as dividend uncertainty, marking-to-market flows, and risk in tracking the stock index with a partial basket of stocks.

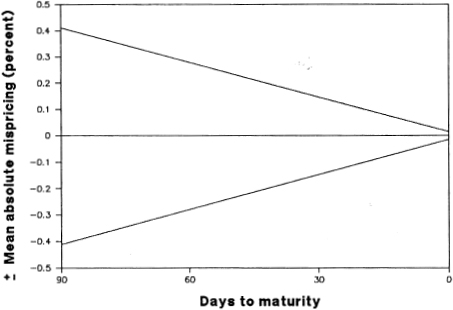
Figure 11.2.  Boundary of mean absolute mispricing as a function of time to maturity.

11.2.4 Path Dependence of Mispricing

We now investigate the path dependence of the mispricing series. One implication of this hypothesis is that, conditional on the mispricing having crossed one arbitrage bound, it is less likely to cross the opposite bound. This phenomenon is a result of the fact that arbitrageurs will unwind positions established when the mispricing was outside one bound before it reaches the other bound.¹⁹ To investigate this issue, we document for each of the 16 contracts the number of upper-bound and lower-bound mispricing violations that occur.²⁰. A tendency for a given contract to have mostly upper-bound violations or mostly lower-bound violations (but not both) is evidence consistent with the mispricing being path-dependent. Indeed, this is the case. Table 11.5 documents the number of upper- and lower-bound violations for each contract. For this table, bounds of –0.6 percent are selected.²¹ With the exception of the September 1983 contract, each contract is dominated by either upper-bound violations or lower-bound violations. For example, the March 1985 contract violated the upper bound 625 times (using 15- minute observations) and did not violate the lower bound for any of the observations. In contrast, the December 1986 contract violated the –0.6 percent mispricing bound 233 times and violated the +0.6 percent bound only two times. Table 11.5 also reports the number of times a given bound was crossed for each contract and the average time (in trading minutes) the mispricing remained outside the bounds. These results indicate that the mispricing remains outside the bounds for a considerable length of time and rules out the possibility that stale prices in the index are a major cause of the observed violations.

 

Table 11.5. Mispricing violations for S&P 500 index futures.

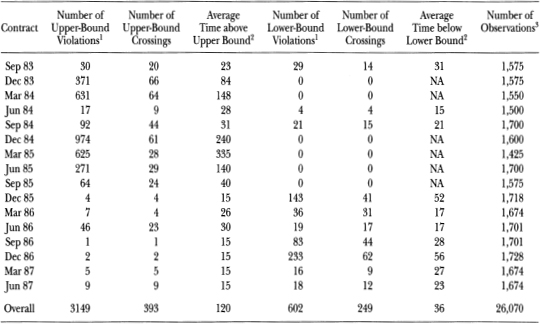
¹The upper bound is set at +0.6 percent and the lower bound at -0.6 percent.

²The average time outside the bounds is in trading minutes.

³The observations are recorded at 15minute intervals.

 

We can develop further evidence of the path dependence of the series by examining conditional probabilities. Consider two possibilities:

 

1. The mispricing is path-independent; following some stochastic process that is pinned to zero at T.
2. The mispricing is path-dependent; conditional on having crossed an upper (lower) bound, the probability of its hitting the lower (upper) bound is smaller.

An implication of argument 1 is that if the mispricing is currently zero, then it is equally likely to hit an upper or a lower bound independent of the past. Argument 2 has a different implication if the mispricing is zero.²² It implies that if the mispricing has crossed the upper bound in the past, it is more likely to continue to deviate above zero and more likely in the future to hit the upper bound than the lower bound. We address this question empirically by identifying all cases where the mispricing crossed the upper or lower bound, returned to zero, and then again crossed the upper or lower bound. For the 16 contracts, there is a total of 142 such cases.

Eighty-two of these cases are instances where the mispricing hits the upper bound, having previously hit a bound and gone to zero. The path independence argument implies the probability of hitting the upper bound, given that the mispricing is currently at zero, is the same whether it had previously hit the upper or lower bound. The estimates of the conditional probabilities from these 82 cases are:

p(x hitting upper bound | x has hit lower bound

and has crossed zero) = 0.36

p(x hitting upper bound | x has hit upper bound

and has crossed zero) = 0.73.

This argument should also hold for violations of the lower bound. For the 60 cases of hitting a bound, crossing zero, and hitting the lower bound, the conditional probability estimates are:

p(x hitting lower bound | x has hit lower bound

and has crossed zero) = 0.64

p(x hitting lower bound | x has hit upper bound

and has crossed zero) = 0.27.

These conditional probabilities differ substantially for the two cases.²³ The evidence is consistent with the notion that the arbitrageurs' option to unwind prematurely introduces path dependence into the mispricing series.

The option to unwind prematurely and the path dependence can also be related to the ability to predict expiration-day movements. Even if during the life of the contract there has been substantial positive (negative) mispricing, often there is also some time prior to expiration when the mispricing is negative (positive). (See the September 1984 contract in Figure 11.1 for an example.) Hence, arbitrageurs will often have had the opportunity to unwind at a profit prior to expiration day, making expiration-day predictions based on the identification of mispricing outside the arbitrage bound difficult.

11.3 Conclusion

We have considered the intraday behavior of the S&P 500 futures and index quotes. Comparisons of the autocorrelations of the changes of the log price of these two series indicate that with a 15-minute observation interval, nonsynchronous trading in the stocks in the index poses a problem. As the interval length is increased, the autocorrelation disappears, with little evidence of the problem with 60-minute observation intervals. We have also examined the relative variability of the futures and spot markets. The results indicate that the futures market is more variable than the spot market even after controlling for problems caused by nonsynchronous prices in the observed index.

Much of this chapter has focused on the behavior of the mispricing series—the difference between the actual futures price and its theoretical value. We had advanced and examined empirically two hypotheses: (1) that the average magnitude of the mispricing increases with time to maturity and (2) that the mispricing series is path-dependent. Evidence supporting these hypotheses has been provided. The results have implications for the width of the arbitrage bounds, the selection of a stochastic process to “model” mispricing, the valuation of options related to the mispricing series, and the prediction of expiration-day movements of the S&P 500 index.

 

---

¹See Cox, Ingersoll, and Ross (1981, p. 340). In later discussion (as also in the empirical Section 11.2) we use the term arbitrageur, consistent with current practice; however, it is clear, as stressed below, that the program trading strategies are not risk-free.

²In this case, investors who already own the basket of stocks represented in the index portfolio are in the best position to undertake the arbitrage; investors who are not already in possession of the index basket would be forced to sell stocks short and would be subject to the “uptick” rule for short sales. For a more complete description of these strategies, see Gould (1987); and for analysis of the hedging costs and effectiveness, see Merrick (1988).

³Beginning with the June 1987 contract, the expiration has shifted to using the opening index price as the cash settlement price for the futures. Therefore, reversal of stock positions would employ market-on-open orders, and these orders also avoid market impact costs.

⁴Modest and Sundaresan (1983) argue that if arbitrageurs lose the interest earnings on a fraction of the proceeds of the short sale of stocks when their strategy calls for shorting stock, then the band would be asymmetric around the “fair” price and would be wider with more time remaining. However, because of the uptick rule, arbitrageurs rarely use short positions in program-driven strategies; they generally employ the pools of stock they own or control if the futures are underpriced.

⁵We use this term only because we lack a less clumsy alternative—we do not mean to imply that every nonzero level of the “mispricing” is evidence of market inefficiency.

⁶We work with the mispricing in relative terms because the major components of the determinant of the bounds should be proportional to the level of the index.

⁷Brennan and Schwartz (1986, 1987) make the argument, as we do here, that the arbitrageurs have the option to close out a position prematurely.

⁸This assumes that the transaction costs are the same for long and short positions in futures and for purchases and sales in stocks. It is not crucial to the analysis.

⁹This depends on whether the automated order-entry system is employed or not. Toward the end of our sample period, the automated order-entry system became the dominant mode of stock-basket trades. Note also that arbitrageurs, because they have finer information regarding bid and asked prices for the component basket of stocks, would be in a position to exploit this information in constructing their strategies.

¹⁰For the March and June 1987 contracts, the CRSP data are not available. We used the daily forecasts of dividend yield (remaining until expiration) on the S&P 500 provided to us by Kidder, Peabody.

¹¹See, for example, Figlewski (1984).

¹²See Kawaller, Koch, and Koch (1987) and Stoll and Whaley (1990) for an analysis of the lead and lag relationships between the two markets.

¹³ This follows from the fact that the price change over an hourly interval is the sum of the four (basic series) price changes over 15-minute intervals. Therefore, the autocorrelation between the lagged price changes at hourly intervals ρ₆₀(1) reflects the autocorrelations from the first lag for 15-minute data to autocorrelations at the seventh lag.

¹⁴The standard deviations for longer intervals are efficiently computed using information from the 15-minute interval. For example, the 60-minuteinterval standard deviation, σ₆₀, is computed from

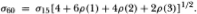
This follows from the fact that the hourly return is the sum of four returns over 15-minute intervals, where these are correlated.

¹⁵The autocorrelations are actually calculated about the mean of the mispricing for the contract, and not around 0.0.

¹⁶Negative autocorrelations at low lags can also be induced by stale prices in the index quotes. However, in the recent contracts (September 1986 through June 1987) the negative autocorrelations are present at the low lags, yet the results of Table 11.1 indicate that the staleprice problem (as measured by the autocorrelation of the index changes) is not important.

¹⁷This z-statistic is corrected for heteroscedasticity and autocorrelation in the regression residual, using the technique of Newey and West (1987). The usual OLS t-statistic for this coefficient is 8.88.

¹⁸We also ran this regression for each of the 16 contracts individually. For 14 of the 16 contracts the estimate of β₁ is positive (although quite variable), and for 11 of the contracts the z-statistics associated with the β₁ estimates are greater than 2.0. For the two contracts where β₁ estimates are negative (September 1984 and September 1986), the z-statistics associated with the estimates (–1.31 and –0.18) are statistically insignificant.

¹⁹We do not consider the possibility that arbitrageurs might roll forward into the next futures contract.

²⁰Stoll and Whaley (1986) also document violations of these bounds. They use hourly observations and assume a constant dividend yield.

²¹ The results are not overly sensitive to the bound selected or to the use of a symmetric bound about zero. We based the selection of 0.6 percent on a round-trip stock commission of 0.70, a round-trip futures commission of 0.08, a market impact cost in futures of 0.05, a market impact in stocks of 0.35, and an index level of 200. We have computed these results with bounds placed at ±0.4 percent and ±0.8 percent, and these show a similar pattern.

²²We also repeated the calculations using symmetric bounds about 0.14 percent (the overall mispricing mean) in place of zero to account for the possibility that a bias in the forward pricing model may be driving the results. The conclusion remains unaffected.

²³ The p-value of a chi-square test of the equality of the conditional probabilities is less than 0.001.