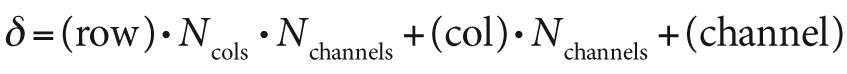There are two things you need to know before we dive into the matrix business. First, there is no "vector" construct in OpenCV. Whenever we want a vector, we just use a matrix with one column (or one row, if we want a transpose or conjugate vector). Second, the concept of a matrix in OpenCV is somewhat more abstract than the concept you learned in your linear algebra class. In particular, the elements of a matrix need not themselves be simple numbers. For example, the routine that creates a new two-dimensional matrix has the following prototype:
CvMat* cvCreateMat ( int rows, int cols, int type );
Here type can be any of a long list of predefined
types of the form: CV_<bit_depth>(S|U|F)
C<number_of_channels>. Thus, the matrix could consist of 32-bit floats
(CV_32FC1), of unsigned integer 8-bit triplets
(CV_8UC3), or of countless other elements. An element
of a CvMat is not necessarily a single number. Being able
to represent multiple values for a single entry in the matrix allows us to do things like
represent multiple color channels in an RGB image. For a simple image containing red, green
and blue channels, most image operators will be applied to each channel separately (unless
otherwise noted).
Internally, the structure of CvMat is relatively
simple, as shown in Example 3-1 (you can see this
for yourself by opening up …/opencv/cxcore/include/cxtypes.h). Matrices have a width, a height, a type, a
step (the length of a row in bytes, not ints or floats), and a pointer to a data array (and some more stuff that we won't talk about just yet). You can
access these members directly by de-referencing a pointer to CvMat or, for some more popular elements, by using supplied accessor functions.
For example, to obtain the size of a matrix, you can get the information you want either by calling cvGetSize(CvMat*), which returns a CvSize structure, or by accessing the height and width independently with such constructs as matrix->height and matrix->width.
Example 3-1. CvMat structure: the matrix "header"
typedef struct CvMat {
int type;
int step;
int* refcount; // for internal use only
union {
uchar* ptr;
short* s;
int* i;
float* fl;
double* db;
} data;
union {
int rows;
int height;
};
union {
int cols;
int width;
};
} CvMat;This information is generally referred to as the matrix header.
Many routines distinguish between the header and the data, the latter being the memory that
the data element points to.
Matrices can be created in one of several ways. The most common way is to use cvCreateMat(), which is essentially shorthand for the
combination of the more atomic functions cvCreateMatHeader() and cvCreateData().
cvCreateMatHeader() creates the CvMat structure without allocating memory for the data, while
cvCreateData() handles the data allocation. Sometimes
only cvCreateMatHeader() is required, either because you
have already allocated the data for some other reason or because you are not yet ready to
allocate it. The third method is to use the cvCloneMat(CvMat*), which creates a new matrix from an existing one.[16] When the matrix is no longer needed, it can be released by calling cvReleaseMat(CvMat**).
The list in Example 3-2 summarizes the functions we have just described as well as some others that are closely related.
Example 3-2. Matrix creation and release
// Create a new rows by cols matrix of type 'type'. // CvMat* cvCreateMat( int rows, int cols, int type ); // Create only matrix header without allocating data // CvMat* cvCreateMatHeader( int rows, int cols, int type ); // Initialize header on existing CvMat structure // CvMat* cvInitMatHeader( CvMat* mat, int rows, int cols, int type, void* data = NULL, int step = CV_AUTOSTEP ); // Like cvInitMatHeader() but allocates CvMat as well. // CvMat cvMat( int rows, int cols, int type, void* data = NULL ); // Allocate a new matrix just like the matrix 'mat'. // CvMat* cvCloneMat( const cvMat* mat ); // Free the matrix 'mat', both header and data. // void cvReleaseMat( CvMat** mat );
Analogously to many OpenCV structures, there is a constructor called cvMat() that creates a CvMat
structure. This routine does not actually allocate memory; it only creates the header (this
is similar to cvInitMatHeader()). These methods are a
good way to take some data you already have lying around, package it by pointing the matrix
header to it as in Example 3-3, and run it
through routines that process OpenCV matrices.
Example 3-3. Creating an OpenCV matrix with fixed data
// Create an OpenCV Matrix containing some fixed data.
//
float vals[] = { 0.866025, -0.500000, 0.500000, 0.866025 };
CvMat rotmat;
cvInitMatHeader(
&rotmat,
2,
2,
CV_32FC1,
vals
);Once we have a matrix, there are many things we can do with it. The simplest operations are
querying aspects of the array definition and data access. To query the matrix, we have cvGetElemType( const CvArr* arr ), cvGetDims( const CvArr* arr, int* sizes=NULL
), and cvGetDimSize( const CvArr* arr, int index
). The first returns an integer constant representing the type of elements
stored in the array (this will be equal to something like CV_8UC1,
CV_64FC4, etc). The second takes the array and an optional pointer to an
integer; it returns the number of dimensions (two for the cases we are considering, but
later on we will encounter N-dimensional matrixlike objects). If the
integer pointer is not null then it will store the height and width (or
N dimensions) of the supplied array. The last function takes an
integer indicating the dimension of interest and simply returns the extent of the matrix in
that dimension.[17]
There are three ways to access the data in your matrix: the easy way, the hard way, and the right way.
The easiest way to get at a member element of an array is with the CV_MAT_ELEM() macro. Thismacro (see Example 3-4) takes the matrix, the type of
element to be retrieved, and the row and column numbers and then returns the
element.
"Under the hood" this macro is just calling the macro CV_MAT_ELEM_PTR(). CV_MAT_ELEM_PTR() (see Example 3-5) takes as arguments the matrix
and the row and column of the desired element and returns (not surprisingly) a pointer
to the indicated element. One important difference between CV_MAT_ELEM() and CV_MAT_ELEM_PTR() is
that CV_MAT_ELEM() actually casts the pointer to the
indicated type before de-referencing it. If you would like to set a value rather than
just read it, you can call CV_MAT_ELEM_PTR()
directly; in this case, however, you must cast the returned pointer to the appropriate
type yourself.
Example 3-5. Setting a single value in a matrix using the CV_MAT_ELEM_PTR() macro
CvMat* mat = cvCreateMat( 5, 5, CV_32FC1 ); float element_3_2 = 7.7; *( (float*)CV_MAT_ELEM_PTR( *mat, 3, 2 ) ) = element_3_2;
Unfortunately, these macros recompute the pointer needed on every call. This means looking up the pointer to the base element of the data area of the matrix, computing an offset to get the address of the information you are interested in, and then adding that offset to the computed base. Thus, although these macros are easy to use, they may not be the best way to access a matrix. This is particularly true when you are planning to access all of the elements in a matrix sequentially. We will come momentarily to the best way to accomplish this important task.
The two macros discussed in "The easy way" are suitable only for accessing one- and two-dimensional arrays (recall that one-dimensional arrays, or "vectors", are really just n-by-1 matrices). OpenCV provides mechanisms for dealing with multidimensional arrays. In fact OpenCV allows for a general N-dimensional matrix that can have as many dimensions as you like.
For accessing data in a general matrix, we use the family of functions cvPtr*D and cvGet*D… listed in Examples Example 3-6 and Example 3-7. The cvPtr*D
family contains cvPtr1D(), cvPtr2D(),
cvPtr3D(), and cvPtrND() …. Each of the
first three takes a CvArr* matrix pointer argument
followed by the appropriate number of integers for the indices, and an optional argument
indicating the type of the output parameter. The routines return a pointer to the
element of interest. With cvPtrND(), the second
argument is a pointer to an array of integers containing the appropriate number of
indices. We will return to this function later. (In the prototypes that follow, you will
also notice some optional arguments; we will address those when we need them.)
Example 3-6. Pointer access to matrix structures
uchar* cvPtr1D( const CvArr* arr, int idx0, int* type = NULL ); uchar* cvPtr2D( const CvArr* arr, int idx0, int idx1, int* type = NULL ); uchar* cvPtr3D( const CvArr* arr, int idx0, int idx1, int idx2, int* type = NULL ); uchar* cvPtrND( const CvArr* arr, int* idx, int* type = NULL, int create_node = 1, unsigned* precalc_hashval = NULL );
For merely reading the data, there is another family of functions cvGet*D, listed in
Example 3-7, that are analogous to those of
Example 3-6 but return the actual value of
the matrix element.
Example 3-7. CvMat and IplImage element functions
double cvGetReal1D( const CvArr* arr, int idx0 ); double cvGetReal2D( const CvArr* arr, int idx0, int idx1 ); double cvGetReal3D( const CvArr* arr, int idx0, int idx1, int idx2 ); double cvGetRealND( const CvArr* arr, int* idx ); CvScalar cvGet1D( const CvArr* arr, int idx0 ); CvScalar cvGet2D( const CvArr* arr, int idx0, int idx1 ); CvScalar cvGet3D( const CvArr* arr, int idx0, int idx1, int idx2 ); CvScalar cvGetND( const CvArr* arr, int* idx );
The return type of cvGet*D is double for four of the routines and CvScalar for the other four. This means that there can be some significant
waste when using these functions. They should be used only where convenient and
efficient; otherwise, it is better just to use cvPtr*D.
One reason it is better to use cvPtr*D() is that
you can use these pointer functions to gain access to a particular point in the matrix
and then use pointer arithmetic to move around in the matrix from there. It is important
to remember that the channels are contiguous in a multichannel matrix. For example, in a
three-channel two-dimensional matrix representing red, green, blue (RGB) bytes, the
matrix data is stored: rgbrgbrgb . . . . Therefore, to move a pointer of the
appropriate type to the next channel, we add 1. If we wanted to go to the next "pixel"
or set of elements, we'd add and offset equal to the number of channels (in this case
3).
The other trick to know is that the step element
in the matrix array (see Examples Example 3-1
and Example 3-2) is the length in bytes of a row in
the matrix. In that structure, cols or width alone is not enough to move between matrix rows
because, for machine efficiency, matrix or image allocation is done to the nearest
four-byte boundary. Thus a matrix of width three bytes would be allocated four bytes
with the last one ignored. For this reason, if we get a byte pointer to a data element
then we add step to the pointer in order to step it
to the next row directly below our point. If we have a matrix of integers or
floating-point numbers and corresponding int or
float pointers to a data element, we would step to
the next row by adding step/4; for doubles, we'd add
step/8 (this is just to take into account that C
will automatically multiply the offsets we add by the data type's byte size).
Somewhat analogous to cvGet*D is cvSet*D in Example 3-8, which sets a matrix or image element with a single call, and the functions cvSetReal*D() and cvSet*D(), which can be used to set the values of elements of a matrix or
image.
Example 3-8. Set element functions for CvMat or IplImage.
void cvSetReal1D( CvArr* arr, int idx0, double value ); void cvSetReal2D( CvArr* arr, int idx0, int idx1, double value ); void cvSetReal3D( CvArr* arr, int idx0, int idx1, int idx2, double value ); void cvSetRealND( CvArr* arr, int* idx, double value ); void cvSet1D( CvArr* arr, int idx0, CvScalar value ); void cvSet2D( CvArr* arr, int idx0, int idx1, CvScalar value ); void cvSet3D( CvArr* arr, int idx0, int idx1, int idx2, CvScalar value ); void cvSetND( CvArr* arr, int* idx, CvScalar value );
As an added convenience, we also have cvmSet()
and cvmGet(), which are used when dealing with
single-channel floating-point matrices. They are very simple:
double cvmGet( const CvMat* mat, int row, int col ) void cvmSet( CvMat* mat, int row, int col, double value )
So the call to the convenience function cvmSet(),
cvmSet( mat, 2, 2, 0.5000 );
is the same as the call to the equivalent cvSetReal2D function,
cvSetReal2D( mat, 2, 2, 0.5000 );
With all of those accessor functions, you might think that there's nothing more to say. In fact, you will rarely use any of the set and get functions. Most of the time, vision is a processor-intensive activity, and you will want to do things in the most efficient way possible. Needless to say, going through these interface functions is not efficient. Instead, you should do your own pointer arithmetic and simply de-reference your way into the matrix. Managing the pointers yourself is particularly important when you want to do something to every element in an array (assuming there is no OpenCV routine that can perform this task for you).
For direct access to the innards of a matrix, all you really need to know is that the data is stored sequentially in raster scan order, where columns ("x") are the fastest-running variable. Channels are interleaved, which means that, in the case of a multichannel matrix, they are a still faster-running ordinal. Example 3-9 shows an example of how this can be done.
When computing the pointer into the matrix, remember that the matrix element
data is a union. Therefore, when de-referencing
this pointer, you must indicate the correct element of the union in order to obtain the
correct pointer type. Then, to offset that pointer, you must use the step element of the matrix. As noted previously, the
step element is in bytes. To be safe, it is best to
do your pointer arithmetic in bytes and then cast to the appropriate type, in this
case float. Although the CvMat structure has the concept of height and width for compatibility with
the older IplImage structure, we use the more
up-to-date rows and cols instead. Finally, note that we recompute ptr for every row rather than simply starting at the beginning and then
incrementing that pointer every read. This might seem excessive, but because the CvMat
data pointer could just point to an ROI within a larger array, there is no guarantee that the data will be contiguous across
rows.
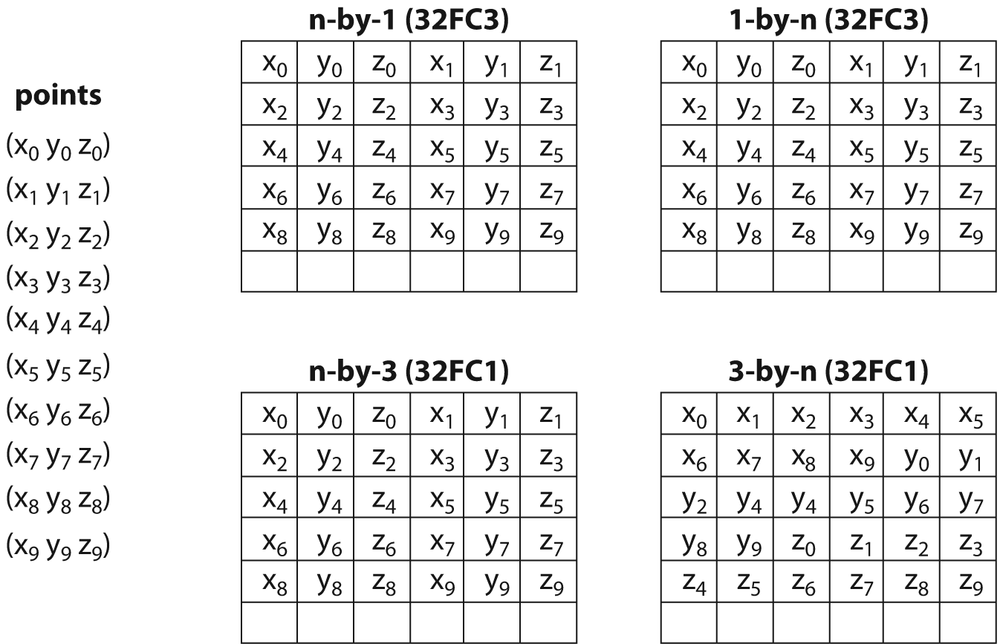
One issue that will come up often—and that is important to understand—is the
difference between a multidimensional array (or matrix) of multidimensional objects and an
array of one higher dimension that contains only one-dimensional objects. Suppose, for
example, that you have n points in three dimensions which you want to
pass to some OpenCV function that takes an argument of type CvMat* (or, more likely, CvArr*). There
are four obvious ways you could do this, and it is absolutely critical to remember that
they are not necessarily equivalent. One method would be to use a two-dimensional array of
type CV32FC1 with n rows and three
columns (n-by-3). Similarly, you could use a two-dimensional array
with three rows and n columns (3-by-n). You
could also use an array with n rows and one column
(n-by-1) of type CV32FC3. Some
of these cases can be freely converted from one to the other (meaning you can just pass
one where the other is expected) but others cannot. To understand why, consider the memory
layout shown in Figure 3-2.
As you can see in the figure, the points are mapped into memory in the same way for three of the four cases just described above but differently for the last. The situation is even more complicated for the case of an N-dimensional array of c-dimensional points. The key thing to remember is that the location of any given point is given by the formula:
Figure 3-2. A set of ten points, each represented by three floating-point numbers, placed in four arrays that each use a slightly different structure; in three cases the resulting memory layout is identical, but one case is different
where Ncols and Nchannels are the number of columns and channels, respectively.[18] From this formula one can see that, in general, an N-dimensional array of c-dimensional objects is not the same as an (N + c)-dimensional array of one-dimensional objects. In the special case of N = 1 (i.e., vectors represented either as n-by-1 or 1-by-n arrays), there is a special degeneracy (specifically, the equivalences shown in Figure 3-2) that can sometimes be taken advantage of for performance.
The last detail concerns the OpenCV data types such as CvPoint2D and CvPoint2D32f. These data types are defined as C structures and
therefore have a strictly defined memory layout. In particular, the integers or
floating-point numbers that these structures comprise are "channel" sequential. As a
result, a one-dimensional C-style array of these objects has the same memory layout as an
n-by-1 or a 1-by-n array of type CV32FC2. Similar reasoning applies for arrays of structures of
the type CvPoint3D32f.
[16] cvCloneMat() and other OpenCV functions
containing the word "clone" not only create a new header that is identical to the input
header, they also allocate a separate data area and copy the data from the source to the
new object.
[17] For the regular two-dimensional matrices discussed here, dimension zero (0) is always the "width" and dimension one (1) is always the height.
[18] In this context we use the term "channel" to refer to the fastest-running index.
This index is the one associated with the C3 part
of CV32FC3. Shortly, when we talk about images, the
"channel" there will be exactly equivalent to our use of "channel" here.