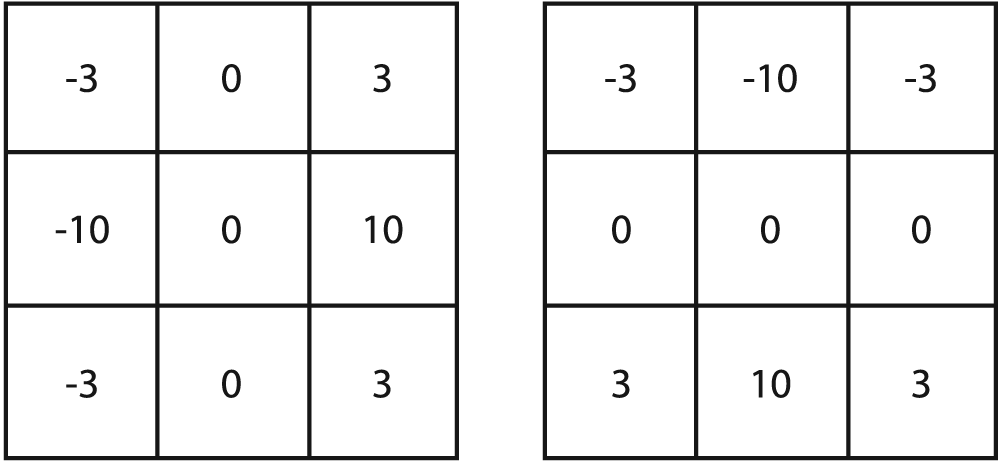
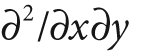One of the most basic and important convolutions is the computation of derivatives (or approximations to them). There are many ways to do this, but only a few are well suited to a given situation.
In general, the most common operator used to represent differentiation is the Sobel derivative [Sobel68] operator (see Figures Figure 6-3 and Figure 6-4). Sobel operators exist for any order of derivative as well as for mixed partial derivatives (e.g.,
Figure 6-3. The effect of the Sobel operator when used to approximate a first derivative in the x-dimension
cvSobel(
const CvArr* src,
CvArr* dst,
int xorder,
int yorder,
int aperture_size = 3
);Here, src and dst
are your image input and output, and xorder and yorder are the orders of the derivative. Typically you'll use 0,
1, or at most 2; a 0 value indicates no derivative in that direction. [65] The aperture_size parameter should be odd and
is the width (and the height) of the square filter. Currently, aperture sizes of 1, 3, 5,
and 7 are supported. If src is 8-bit then the dst must be of depth IPL_DEPTH_16S to avoid overflow.
Figure 6-4. The effect of the Sobel operator when used to approximate a first derivative in the y-dimension
Sobel derivatives have the nice property that they can be defined for kernels of any size, and those kernels can be constructed quickly and iteratively. The larger kernels give a better approximation to the derivative because the smaller kernels are very sensitive to noise.
To understand this more exactly, we must realize that a Sobel derivative is not really a derivative at all. This is because the Sobel operator is defined on a discrete space. What the Sobel operator actually represents is a fit to a polynomial. That is, the Sobel derivative of second order in the x-direction is not really a second derivative; it is a local fit to a parabolic function. This explains why one might want to use a larger kernel: that larger kernel is computing the fit over a larger number of pixels.
In fact, there are many ways to approximate a derivative in the case of a discrete
grid. The downside of the approximation used for the Sobel operator is that it is less accurate for small kernels. For large
kernels, where more points are used in the approximation, this problem is less
significant. This inaccuracy does not show up directly for the X and
Y filters used in cvSobel(),
because they are exactly aligned with the x- and
y-axes. The difficulty arises when you want to make image
measurements that are approximations of directional derivatives
(i.e., direction of the image gradient by using the arctangent of the
y/x filter responses).
To put this in context, a concrete example of where you may want image measurements of this kind would be in the process of collecting shape information from an object by assembling a histogram of gradient angles around the object. Such a histogram is the basis on which many common shape classifiers are trained and operated. In this case, inaccurate measures of gradient angle will decrease the recognition performance of the classifier.
For a 3-by-3 Sobel filter, the inaccuracies are more apparent the further the gradient
angle is from horizontal or vertical. OpenCV addresses this inaccuracy for small (but
fast) 3-by-3 Sobel derivative filters by a somewhat obscure use of the special aperture_size value CV_SCHARR in the cvSobel() function. The
Scharr filter is just as fast but more accurate than the Sobel filter, so it
should always be used if you want to make image measurements using a 3-by-3 filter. The
filter coefficients for the Scharr filter are shown in Figure 6-5 [Scharr00].