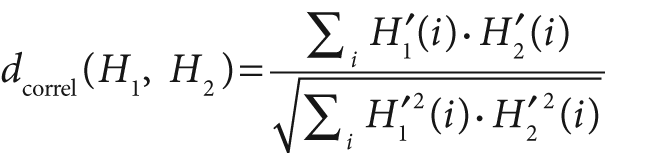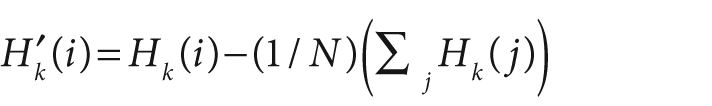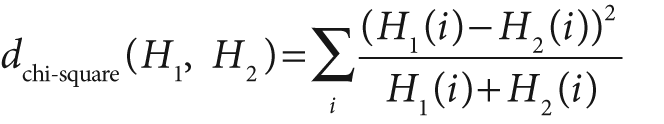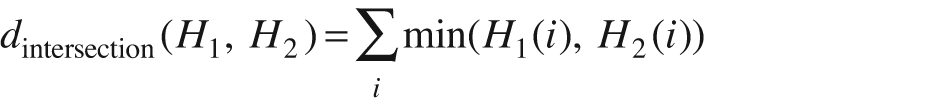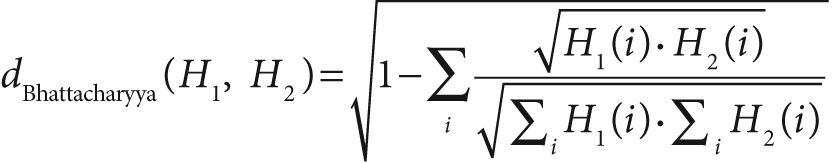Now that we have this great data structure, we will naturally want to do some fun stuff with it. First let's hit some of the basics that will be used over and over; then we'll move on to some more complicated features that are used for more specialized tasks.
When dealing with a histogram, we typically just want to accumulate information into its various bins. Once we have done this, however, it is often desirable to work with the histogram in normalized form, so that individual bins will then represent the fraction of the total number of events assigned to the entire histogram:
cvNormalizeHist( CvHistogram* hist, double factor );
Here hist is your histogram and factor is the number to which you would like to normalize the
histogram (which will usually be 1). If you are following closely then you may have noticed
that the argument factor is a double although the internal data type of CvHistogram is always float—further evidence
that OpenCV is a work in progress!
The next handy function is the threshold function:
cvThreshHist( CvHistogram* hist, double factor );
The argument factor is the cutoff for the threshold.
The result of thresholding a histogram is that all bins whose value is below the threshold
factor are set to 0. Recalling the image thresholding function cvThreshold(), we might say that the histogram thresholding function is
analogous to calling the image threshold function with the argument threshold_type set to CV_THRESH_TOZERO.
Unfortunately, there are no convenient histogram thresholding functions that provide
operations analogous to the other threshold types. In practice, however, cvThreshHist() is the one you'll probably want because with real
data we often end up with some bins that contain just a few data points. Such bins are
mostly noise and thus should usually be zeroed out.
Another useful function is cvCopyHist(), which (as
you might guess) copies the information from one histogram into another.
void cvCopyHist(const CvHistogram* src, CvHistogram** dst );
This function can be used in two ways. If the destination histogram *dst is a histogram of the same size as src, then both the data and the bin ranges from src will be copied into *dst. The other way
of using cvCopyHist() is to set *dst to NULL. In this case, a new histogram
will be allocated that has the same size as src and then
the data and bin ranges will be copied (this is analogous to the image function cvCloneImage()). It is to allow this kind of cloning that the
second argument dst is a pointer to a pointer to a
histogram—unlike the src, which is just a pointer to a
histogram. If *dst is NULL when cvCopyHist() is called, then
*dst will be set to the pointer to the newly allocated
histogram when the function returns.
Proceeding on our tour of useful histogram functions, our next new friend is cvGetMinMaxHistValue(), which reports the minimal and maximal
values found in the histogram.
void cvGetMinMaxHistValue(
const CvHistogram* hist,
float* min_value,
float* max_value,
int* min_idx = NULL,
int* max_idx = NULL
);Thus, given a histogram hist, cvGetMinMaxHistValue()
will compute its largest and smallest values. When the function returns, *min_value and *max_value
will be set to those respective values. If you don't need one (or both) of these results,
then you may set the corresponding argument to NULL. The
next two arguments are optional; if you leave them set to their default value (NULL), they will do nothing. However, if they are non-NULL pointers to int then the
integer values indicated will be filled with the location index of the minimal and maximal
values. In the case of multi-dimensional histograms, the arguments min_idx and
max_idx (if not NULL) are assumed to point to an array of integers whose length is equal to the
dimensionality of the histogram. If more than one bin in the histogram has the same minimal
(or maximal) value, then the bin that will be returned is the one with the smallest index
(in lexicographic order for multidimensional histograms).
After collecting data in a histogram, we often use cvGetMinMaxHistValue() to find the minimum value and then "threshold away" bins
with values near this minimum using cvThreshHist() before
finally normalizing the histogram via cvNormalizeHist().
Last, but certainly not least, is the automatic computation of histograms from images.
The function cvCalcHist() performs this crucial
task:
void cvCalcHist(
IplImage** image,
CvHistogram* hist,
int accumulate = 0,
const CvArr* mask = NULL
);The first argument, image, is a pointer to an array
of IplImage* pointers. [95] This allows us to pass in many image planes. In the case of a multi-channel
image (e.g., HSV or RGB) we will have to cvSplit() (see
Chapter 3 or Chapter 5) that image
into planes before calling cvCalcHist(). Admittedly
that's a bit of a pain, but consider that frequently you'll also want to pass in multiple
image planes that contain different filtered versions of an image'for example, a plane of
gradients or the U- and V-planes of YUV. Then what a mess it
would be when you tried to pass in several images with various numbers of channels (and you
can be sure that someone, somewhere, would want just some of those channels in those
images!). To avoid this confusion, all images passed to cvCalcHist() are assumed (read "required") to be single-channel images. When
the histogram is populated, the bins will be identified by the tuples formed across
these multiple images. The argument hist must be a
histogram of the appropriate dimensionality (i.e., of dimension equal to the number of image
planes passed in through image). The last two arguments
are optional. The accumulate argument, if nonzero,
indicates that the histogram hist should not be cleared
before the images are read; note that accumulation allows cvCalcHist() to be called multiple times in a data collection loop. The final
argument, mask, is the usual optional Boolean mask; if
non-NULL, only pixels corresponding to nonzero entries
in the mask image will be included in the computed histogram.
Yet another indispensable tool for working with histograms, first introduced by Swain
and Ballard [Swain91] and further generalized by Schiele and Crowley [Schiele96], is the
ability to compare two histograms in terms of some specific criteria for similarity. The
function cvCompareHist() does just this.
double cvCompareHist(
const CvHistogram* hist1,
const CvHistogram* hist2,
int method
);The first two arguments are the histograms to be compared, which should be of the same size. The third argument is where we select our desired distance metric. The four available options are as follows.
where
and N equals the number of bins in the histogram.
For correlation, a high score represents a better match than a low score. A perfect match is 1 and a maximal mismatch is –1; a value of 0 indicates no correlation (random association).
For chi-square, [96]a low score represents a better match than a high score. A perfect match is 0 and a total mismatch is unbounded (depending on the size of the histogram).
For histogram intersection, high scores indicate good matches and low scores indicate bad matches. If both histograms are normalized to 1, then a perfect match is 1 and a total mismatch is 0.
For Bhattacharyya matching [Bhattacharyya43], low scores indicate good matches and high scores indicate bad matches. A perfect match is 0 and a total mismatch is a 1.
With CV_COMP_BHATTACHARYYA, a special factor in
the code is used to normalize the input histograms. In general, however, you should
normalize histograms before
comparing them because concepts like histogram intersection make little
sense (even if allowed) without normalization.
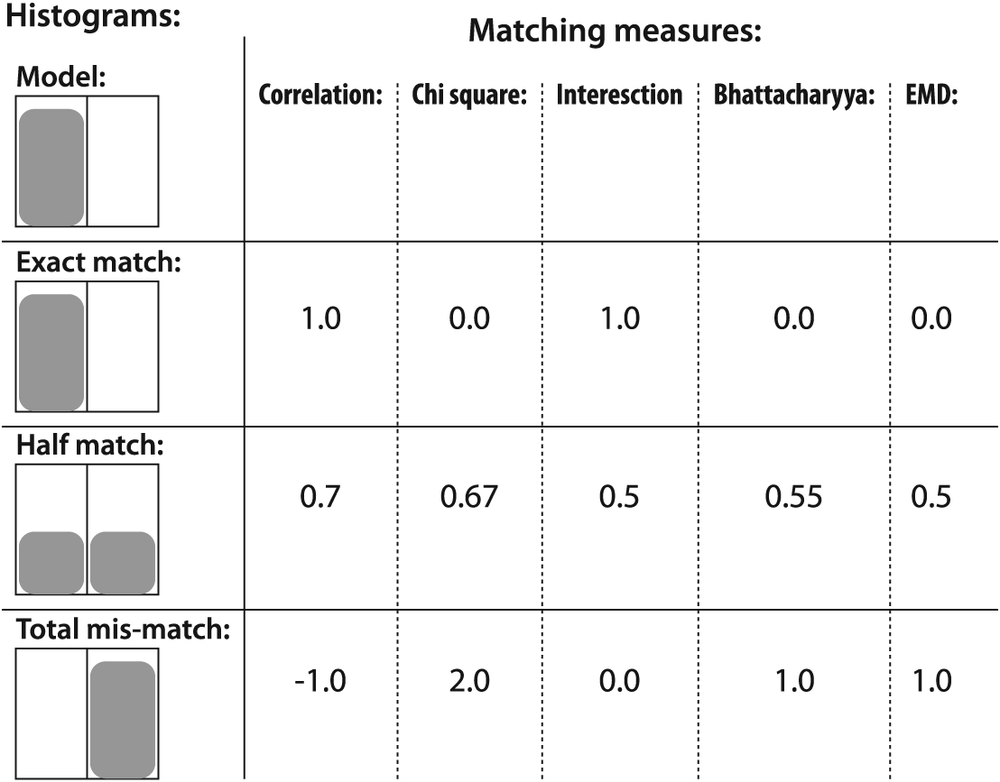
The simple case depicted in Figure 7-4 should clarify matters. In fact, this is about the simplest case that could be imagined: a one-dimensional histogram with only two bins. The model histogram has a 1.0 value in the left bin and a 0.0 value in the right bin. The last three rows show the comparison histograms and the values generated for them by the various metrics (the EMD metric will be explained shortly).
Figure 7-4 provides a quick reference for the behavior of different matching types, but there is something disconcerting here, too. If histogram bins shift by just one slot—as with the chart—s first and third comparison histograms'then all these matching methods (except EMD) yield a maximal mismatch even though these two histograms have a similar "shape". The rightmost column in Figure 7-4 reports values returned by EMD, a type of distance measure. In comparing the third to the model histogram, the EMD measure quantifies the situation precisely: the third histogram has moved to the right by one unit. We shall explore this measure further in the "Earth Mover's Distance" section to follow.
In the authors' experience, intersection works well for quick-and-dirty matching and chi-square or Bhattacharyya work best for slower but more accurate matches. The EMD measure gives the most intuitive matches but is much slower.
It's probably time for some helpful examples. The program in Example 7-1 (adapted from the OpenCV code bundle) shows how we can use some of the functions just discussed. This program computes a hue-saturation histogram from an incoming image and then draws that histogram as an illuminated grid.
Example 7-1. Histogram computation and display
#include <cv.h>
#include <highgui.h>
int main( int argc, char** argv ) {
IplImage* src;
if( argc == 2 && (src=cvLoadImage(argv[1], 1))!= 0) {
// Compute the HSV image and decompose it into separate planes.
//
IplImage* hsv = cvCreateImage( cvGetSize(src), 8, 3 );
cvCvtColor( src, hsv, CV_BGR2HSV );
IplImage* h_plane = cvCreateImage( cvGetSize(src), 8, 1 );
IplImage* s_plane = cvCreateImage( cvGetSize(src), 8, 1 );
IplImage* v_plane = cvCreateImage( cvGetSize(src), 8, 1 );
IplImage* planes[] = { h_plane, s_plane };
cvCvtPixToPlane( hsv, h_plane, s_plane, v_plane, 0 );
// Build the histogram and compute its contents.
//
int h_bins = 30, s_bins = 32;
CvHistogram* hist;
{
int hist_size[] = { h_bins, s_bins };
float h_ranges[] = { 0, 180 }; // hue is [0,180]
float s_ranges[] = { 0, 255 };
float* ranges[] = { h_ranges, s_ranges };
hist = cvCreateHist(
2,
hist_size,
CV_HIST_ARRAY,
ranges,
1
);
}
cvCalcHist( planes, hist, 0, 0 ); //Compute histogram
cvNormalizeHist( hist[i], 1.0 ); //Normalize it
// Create an image to use to visualize our histogram.
//
int scale = 10;
IplImage* hist_img = cvCreateImage(
cvSize( h_bins * scale, s_bins * scale ),
8,
3
);
cvZero( hist_img );
// populate our visualization with little gray squares.
//
float max_value = 0;
cvGetMinMaxHistValue( hist, 0, &max_value, 0, 0 );
for( int h = 0; h < h_bins; h++ ) {
for( int s = 0; s < s_bins; s++ ) {
float bin_val = cvQueryHistValue_2D( hist, h, s );
int intensity = cvRound( bin_val * 255 / max_value );
cvRectangle(
hist_img,
cvPoint( h*scale, s*scale ),
cvPoint( (h+1)*scale - 1, (s+1)*scale - 1),
CV_RGB(intensity,intensity,intensity),
CV_FILLED
);
}
}
cvNamedWindow( "Source", 1 );
cvShowImage( "Source", src );
cvNamedWindow( "H-S Histogram", 1 );
cvShowImage( "H-S Histogram", hist_img );
cvWaitKey(0);
}
}In this example we have spent a fair amount of time preparing the arguments for
cvCalcHist(), which is not uncommon. We also chose to
normalize the colors in the visualization rather than normalizing the histogram itself,
although the reverse order might be better for some applications. In this case it gave us
an excuse to call cvGetMinMaxHistValue(), which was
reason enough not to reverse the order.
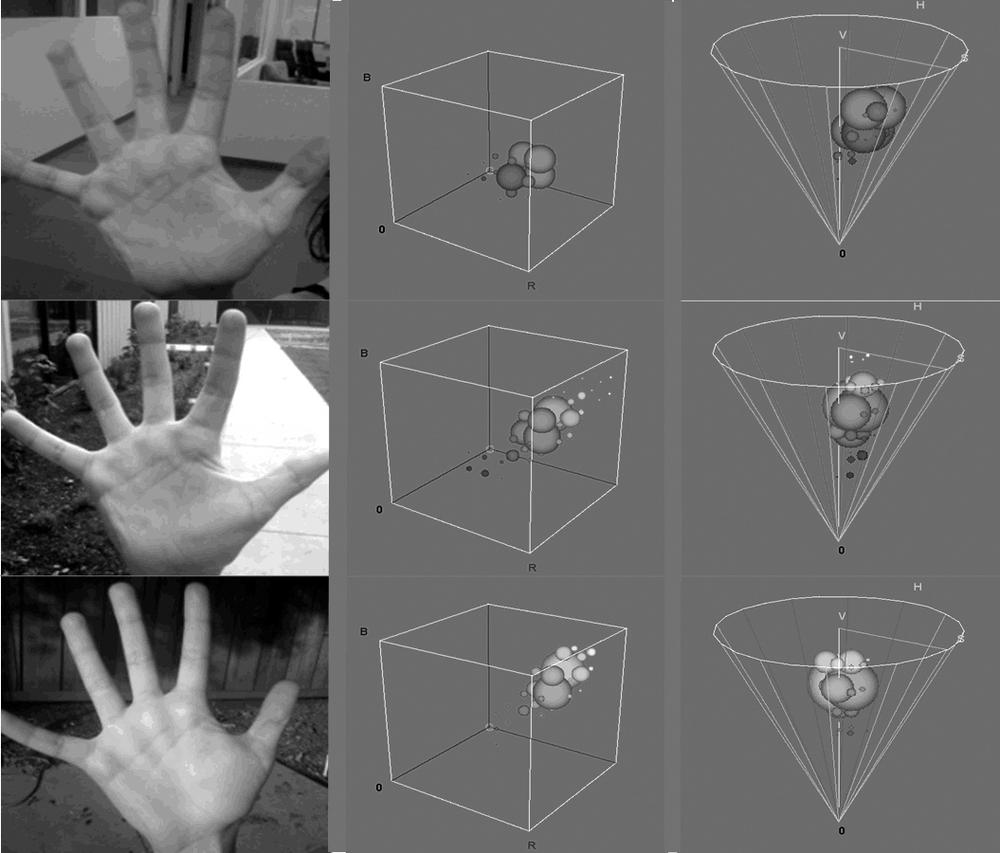
Let's look at a more practical example: color histograms taken from a human hand under various lighting conditions. The left column of Figure 7-5 shows images of a hand in an indoor environment, a shaded outdoor environment, and a sunlit outdoor environment. In the middle column are the blue, green, and red (BGR) histograms corresponding to the observed flesh tone of the hand. In the right column are the corresponding HSV histograms, where the vertical axis is V (value), the radius is S (saturation) and the angle is H (hue). Notice that indoors is darkest, outdoors in the shade brighter, and outdoors in the sun brightest. Observe also that the colors shift around somewhat as a result of the changing color of the illuminating light.
As a test of histogram comparison, we could take a portion of one palm (e.g., the top half of the indoor palm), and compare the histogram representation of the colors in that image either with the histogram representation of the colors in the remainder of that image or with the histogram representations of the other two hand images. Flesh tones are often easier to pick out after conversion to an HSV color space. It turns out that restricting ourselves to the hue and saturation planes is not only sufficient but also helps with recognition of flesh tones across ethnic groups. The matching results for our experiment are shown in Table 7-1, which confirms that lighting can cause severe mismatches in color. Sometimes normalized BGR works better than HSV in the context of lighting changes.