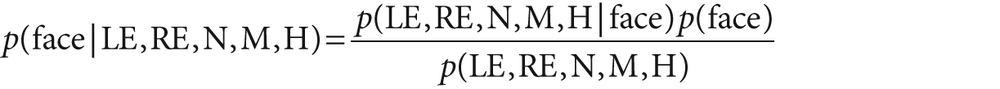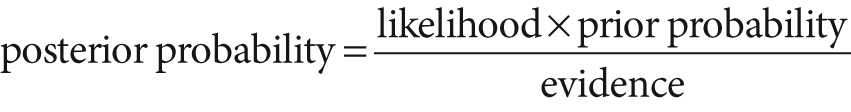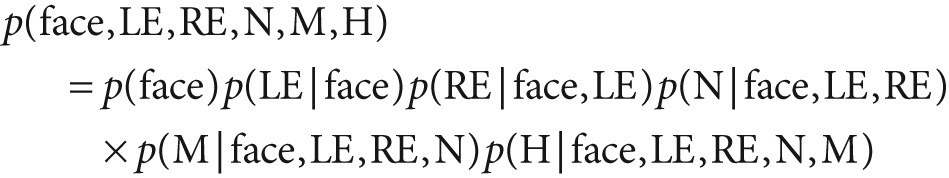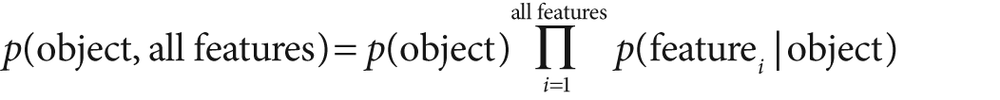The preceding routines are from cxcore. We'll now
start discussing the machine learning (ML) library section of OpenCV. We'll begin with
OpenCV's simplest supervised classifier, CvNormalBayesClassifier, which is called both a normal
Bayes classifier and a naïve Bayes classifier. It's
"naïve" because it assumes that all the features are independent from one another even though this is seldom the case
(e.g., finding one eye usually implies that another eye is lurking nearby). Zhang discusses
possible reasons for the sometimes surprisingly good performance of this classifier
[Zhang04]. Naïve Bayes is not used for regression, but it's an effective classifier that can
handle multiple classes, not just two. This classifier is the simplest possible case of what
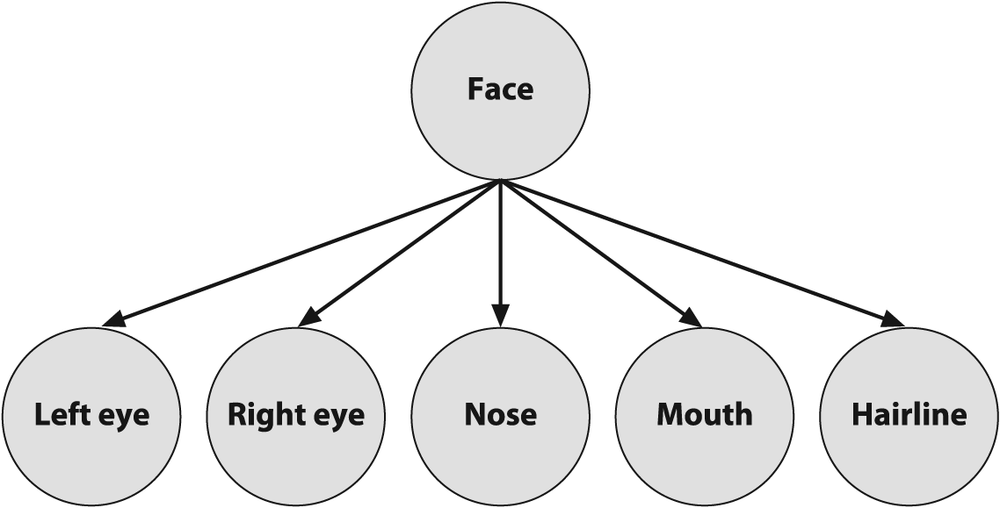
is now a large and growing field known as Bayesian networks, or "probabilistic graphical models". Bayesian networks are causal models; in Figure 13-6, for example, the face features in an
image are caused by the existence of a face. In use, the face variable is considered a
hidden variable and the face features—via image processing operations
on the input image—constitute the observed evidence for the existence of a face. We call
this a generative model because the face causally generates the face
features. Conversely, we might start by assuming the face node is active and then randomly
sample what features are probabilistically generated given that face is active.[244] This top-down generation of data with the same statistics as the learned causal
model (here, the face) is a useful ability that a purely discriminative model does not possess. For example, one might generate faces for
computer graphics display, or a robot might literally "imagine" what it should do next by
generating scenes, objects, and interactions. In contrast to Figure 13-6, a discriminative model would have
the direction of the arrows reversed.
Figure 13-6. A (naïve) Bayesian network, where the lower-level features are caused by the presence of an object (the face)
Bayesian networks are a deep and initially difficult field to understand, but the naïve Bayes algorithm derives from a simple application of Bayes' law. In this case, the probability (denoted p) of a face given the features (denoted, left to right in Figure 13-6, as LE, RE, N, M, H) is:
Just so you'll know, in English this equation means:
In practice, we compute some evidence and then decide what object caused it. Since the computed evidence stays the same for the objects, we can drop that term. If we have many models then we need only find the one with the maximum numerator. The numerator is exactly the joint probability of the model with the data: p(face, LE, RE, N, M, H). We can then use the definition of conditional probability to derive the joint probability:
Applying our assumption of independence of features, the conditional features drop out. So, generalizing face to "object" and particular features to "all features", we obtain the reduced equation:
To use this as an overall classifier, we learn models for the objects that we want. In run mode we compute the features and find the object that maximizes this equation. We typically then test to see if the probability for that "winning" object is over a given threshold. If it is, then we declare the object to be found; if not, we declare that no object was recognized.
Tip
If (as frequently occurs) there is only one object of interest, then you might ask: "The probability I'm computing is the probability relative to what?" In such cases, there is always an implicit second object—namely, the background—which is everything that is not the object of interest that we're trying to learn and recognize.
Learning the models is easy. We take many images of the objects; we then compute features over those objects and compute the fraction of how many times a feature occurred over the training set for each object. In practice, we don't allow zero probabilities because that would eliminate the chance of an object existing; hence zero probabilities are typically set to some very low number. In general, if you don't have much data then simple models such as naïve Bayes will tend to outperform more complex models, which will "assume" too much about the data (bias).
The training method for the normal Bayes classifier is:
bool CvNormalBayesClassifier::train( const CvMat* _train_data, const CvMat* _responses, const CvMat* _var_idx = 0, const CvMat* _sample_idx = 0, bool update = false );
This follows the generic method for training described previously, but it allows only
data for which each row is a training point (i.e., as if tflag=CV_ROW_SAMPLE). Also, the input _train_data is a single-column CV_32FC1
vector that can only be of type ordered, CV_VAR_ORDERED
(numbers). The output label _responses is a vector
column that can only be of categorical type CV_VAR_CATEGORICAL (integers, even if contained in a float vector). The
parameters _var_idx and _sample_idx are optional; they allow you to mark (respectively) features and
data points that you want to use. Mostly you'll use all features and data and simply pass
NULL for these vectors, but _sample_idx can be used to divide the training and test sets, for example.
Both vectors are either single-channel integer (CV_32SC1) zero-based indexes or 8-bit (CV_8UC1) mask values, where 0 means to skip. Finally, update can be set to merely update the normal Bayes learning
rather than to learn a new model from scratch.
The prediction for method for CvNormalBayesClassifier computes the most probable class for its input
vectors. One or more input data vectors are stored as rows of the samples matrix. The predictions are returned in corresponding rows of the
results vector. If there is only a single input in
samples, then the resulting prediction is returned as a float value by the predict method and the results array may be set to NULL (the default). The format for the prediction
method is:
float CvNormal BayesClassifier::predict( const CvMat* samples, CvMat* results = 0 ) const;
We move next to a discussion of tree-based classifiers.
[244] Generating a face would be silly with the naïve Bayes algorithm because it assumes independence of features. But a more general Bayesian network can easily build in feature dependence as needed.