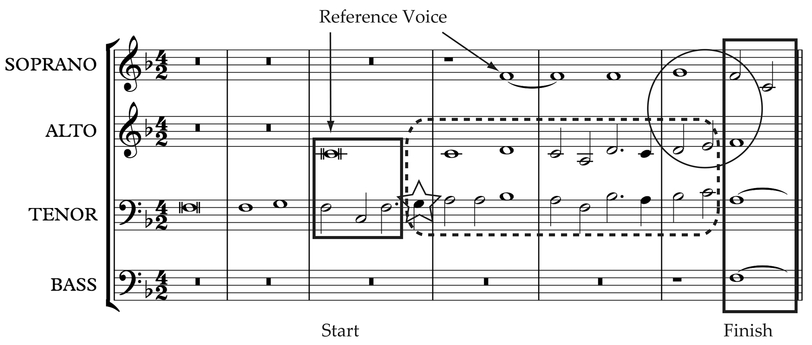
Figure 13.1 Giovanni di Palestrina, “Sicut cervus,” mm. 1–7.
Melody, Texture, and Harmony in the Classical Tradition
Robert Gjerdingen
Tremendous strides have been made in recent decades in our understanding of how composers in the European classical tradition learned their craft. That new understanding bears little resemblance to the ahistorical chord-centered simplifications taught in collegiate harmony classes. Because a significant gap exists between the complex mental representations learned by European composers and the simplistic harmony-class assumptions often underlying experiments in music cognition, this chapter seeks to bridge that gap by sketching a historically defensible outline of musical structure as it was understood by its “native speakers.” Aside from a tantalizing study by Meyer and Rosner (1982), hardly any investigations of “historically informed” listening have been undertaken. This chapter presents a number of ideas to stimulate such studies in the future.
From the time of Charlemagne (ca. 800 CE), the liturgical chants now known as Gregorian Chant (after Pope Gregory I) formed a bedrock of organized religious expression in both churches and monasteries (Hiley, 1993, p. 479). As a sacred heritage, the melodies of these chants could not, in general, be altered. One could, however, embellish them in a process called “troping.” Troping was a general Medieval practice. Verbally, a phrase like “Ave Maria, gratia plena” (Hail Mary, full of grace) might be troped as “Ave Maria celi regina, gratia plena” (Hail Mary, Queen of heaven, full of grace). The original text remains, but an extra thought amplifies and decorates it. Musically, one could trope a chant by adding a second voice to it. Polyphony (music with more than one voice or instrument) and counterpoint (the art of placing one note or “point” against another in stylistically appropriate ways— punctus contra punctum) thus have their origins in the desire of musicians to exalt and amplify an important chant (Burkholder, et al., 2010, p. 84).
In polyphony, chant served as a reference or cognitive anchor from which the cantor who improvised the embellishing voice took his bearings. The beginnings and endings of phrases in the reference chant would be aurally marked by “perfect intervals,” the word perfect meaning complete and stable (Lat.: perfecta (Fuller, 1992). By contrast, the internal tones of phrases could have “imperfect intervals.” The perfect intervals had perceptually simpler frequency ratios (1:1, 1:2, 2:3, or in musicians’ language “unisons, octaves, and fifths”) and the imperfect intervals had more complex ratios (musical “thirds and sixths”). Thus the closure of phrase boundaries correlated with increased consonance, while the sense of instability and the need to move forward correlated with decreased consonance or even dissonance. A listener’s ability to anticipate a satisfying close on a perfect interval was aided by the compositional use of stereotyped and coordinated melodic formulas in both voices, formulas that habitually terminated on the final tone of a phrase.
In the late 1200s a system of “mensural” (measured) music evolved, where differently shaped notes represented tones of different durations. In many respects that same system has been retained until the present day in standard music notation. The new ability provided by this system of notation—to coordinate time within and between voices—allowed for the construction, manipulation, and transmission of a perceptually active metrical grid, with pulses or beats that could alternate as perceptually “strong” and “weak.” Traditional and improvised musics have had musical meters for thousands of years, but mensural notation allowed for a higher degree of advance planning and the control of voice-to-voice interactions. In about the year 1280, a monk named Franco of Cologne (fl. mid-13th cent.) set forth the “Franconian Rule” whereby, expressed in modern terms, he stated that consonance should be correlated with metrical strength. Metrically strong and salient moments required stability and consonance, while metrically weak and inconspicuous moments could feature imperfect consonances and fleeting dissonances: In his words, “Let it be understood that in all rhythmic modes one must employ consonances at the beginning of each perfection” (quoted in Gerbert, 1784, p. 13).
For an illustration of these principles in the late Renaissance, let us examine the opening phrase of a sacred motet (“Sicut cervus,” 1584) by the Pope’s head musician: Palestrina (ca. 1525–1594) (see Figure 13.1).
Figure 13.1 Giovanni di Palestrina, “Sicut cervus,” mm. 1–7.
Counterpoint begins between the alto and tenor voices in measure 3. As shown by the rectangles overlaid on the notation, those two voices start with perfect consonances (fifths and an octave), and three of the four voices finish the phrase with perfect consonances. In between, the dashed line encloses a series of imperfect consonances (major and minor thirds). In this style of music, no single voice serves as a fixed reference voice. The role of reference voice shifts among the four voices, being defined by relative stability. Practically speaking, that meant that the tone with the longest duration within a given passage tended to take on the role of stable anchor and reference. The star over the tone G3 indicates a dissonance that, following the Franconian Rule, is placed at a very weak location in the metrical grid. By measure 5, the soprano voice takes on the role of reference voice due to its relative stability compared to the more mobile tenor and alto. Those two voices perform in tandem what was once called “gymel” (“twins”) (cf. Bukofzer, 1935); the term indicates how performers and listeners were influenced by the effects of auditory streaming to think of two such voices as being closely related, sharing, in Gestalt terms, a “common fate” (see Lee, this volume). The circle around the soprano and alto at the end of the passage indicates a stereotyped closing gesture or “cadence” (Janin, 2012).
Note that Palestrina was able to satisfy and artistically exploit all these constraints while simultaneously beginning each voice with nearly the same melody in the manner of a round or fugue. Such an esoteric art required many years of training, beginning at around seven years of age in service as a choirboy. The choirboy’s daily experience of chant and polyphony, along with training in how to improvise a counterpoint to a “fixed song” (cantus firmus, meaning an isochronous reference voice), helped prepare future composers and improvisers. The melodic style absorbed from this training favored easily sung intervals in predominantly stepwise motion (see Shanahan, this volume). A number of traits in Palestrina’s melodic contours can be traced to an avoidance of patterns that were difficult to sing accurately and securely (Cohen, 1971).
The texture of sacred polyphony in the late 1500s was complex, with from three to twelve notated voices moving in a number of perceived auditory streams. The gymel in Figure 13.1 (tenor and alto “twins”) indicates how correlated or “parallel” motion between voices could reduce the number of perceived streams. If one thinks of melodic motion as taking place in a two-dimensional space of time and pitch, there are only three basic directions possible: Up, down, or “sideways” (meaning repetition of the same pitch). In a four-voice motet like that shown in Figure 13.1, three voices can move in three different directions but a fourth voice will need to duplicate one of those directions. In a six-voice motet there are fifteen nominal voice pairs, but a listener cannot perceive that many contrapuntal relationships (Huron, 1989).
As the number of voices increased there were offsetting simplifications that kept a listener’s processing load within a reasonable range. In one reduction, multi-voice sonorities, which could appear in hundreds of unique configurations, came to be treated categorically. Accompanists in the early 1600s developed a numerical shorthand to help them recognize the global nature of collective sonorities. Given the requirements for voice-pair consonances, there emerged only two consonant multi-voice sonorities: A 1/3/5 “chord” (meaning a sonority comprising a bass tone and the intervals of a third and fifth above it, e.g., the tones C4–E4–G4 or their octave duplications) and a 1/3/6 chord (e.g., C4–E4–A4). A bass with numerical figures above or below it was called a “figured bass.” The default sonority was 1/3/5, which received no figure. The other sonority, 1/3/6, was marked by a “6,” which highlighted the difference from the default case. Any important dissonance was indicated by its particular interval above the bass (Arnold, 1931). The result was that the three old categories of two-note intervals—perfect, imperfect, and dissonant—transformed into three categories of multi-note sonorities—plain triads (1–3–5), “sixth” chords (1–3–6), and all dissonant combinations.
A second simplification involved the coordination of larger contrapuntal patterns with longer and more hierarchically differentiated musical meters (McClary, 2012, 241ff.). In the sacred style of Palestrina, meter was perceptually present largely as a simple alternation of strong and weak beats. Most instantiations of the Franconian Rule, for instance, only concerned one or two adjacent beats. A listener was thus rarely able to predict the course of musical events beyond the next beat or two. Even the longest stereotyped cadence formulas extended to only four or five adjacent beats. By contrast, musical patterns of much longer temporal spans developed during the course of the 1600s, supported and made salient by more complex meters. An important characteristic of these extended patterns was the listener’s ability to connect and associate nonadjacent events (Gjerdingen, 2014). Figure 13.2 shows measures 6–11 of the first movement of Antonio Vivaldi’s Concerto in C Major for Recorder (RV444).
Figure 13.2 Antonio Vivaldi, Concerto in C Major for Recorder (RV444), Mvt. 1, mm. 6–11.
Note how a model pattern (“Model” in Figure 13.2) of twenty-four tones in the melody recurs three more times in copies, each of which is transposed downward one step of the scale. The most salient tones, annotated on the score with Arabic numerals in circles, coincide with the strongest moments in the meter, i.e., the downbeats of each measure. Those Arabic numerals indicate the position of the salient tones in terms of a governing scale. The idea of a governing scale with perceptually recognizable locations (musicians say “steps” or “degrees”) indicates a hierarchy of pitch relationships in tandem with the hierarchy of metrical relationships. This is what is meant by “key” in musicians’ parlance, and contrasts to the more localized tonal and metrical patterns in the music of Palestrina and many other early composers.
Focusing on the remarkably large and innovative hierarchies of tones and moments in Vivaldi's score may cause observers to overlook how many of the prior traditions had nevertheless been retained. Take for instance the tones marked by numbers in circles. Scale degrees 
in the melody are matched with 
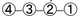in the bass. In other words, the core tones of the melody and bass are performing gymel, the centuries-old tradition of counterpoints that were improvised ill parallel imperfect consonances (here thirds, separated by additional octaves).. This is true even though the tones are no longer adjacent in their voices' time series. These core tones have perceived similarity from their similar positions in the meter and can thus perceptually "pop out" from the background in accordance with Gestalt principles of pattern recognition.
The figured bass indicates a syntax of sonorities that also has many features in common with the phraseology of much older two-voice counterpoint. The first core event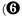 
in the melody, 
in the bass) has the default 1/3/5 sonority (F4-A4—C5) and thus receives no figure. At the next two core events the figure "6" indicates less stability, suggesting a continuation to the final 1/3/5 event 
in the melody, 
in the bass). Plain 1/3/5 "triads" thus took over some of the syntactical meanings of perfect consonances, while "6-chords" (e.g., 1/3/6 sonorities) became the analogues of imperfect consonances—"6," after all, is an imperfect consonance (Holtmeier, 2007).
In Vivaldi's era this ancient syntax of stable perfection and unstable imperfection became tied explicitly to scale steps through what was known as the "Rule of the Octave" (Christensen, 1992). As taught to young musicians, the Rule encapsulated a quite specific linkage of four factors: Scale step, contour in the bass, perfection/imperfection, and dissonance. In a fascinating cross- domain mapping, the correlation of intervallic perfection with beginning and ending points in time was transferred to a correlation of chordal perfection with the tonic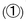 
and dominant 
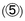notes of the scale. Something of this idea is retained in current French terminology, where a 1/3/5 triad is still termed an accord parfait (perfect). All the other degrees of the scale should have "6" chords. The diagram in Figure 13.3 presents an illustrative outline of the Rule of the Octave.
Circled numbers indicate degrees or steps of the governing scale or key. The boldface "5"s indicate 1/3/5 triads on the important tonic and dominant tones of the scale (unchanging for both major and minor modes). The "6"s show how sixth-chords fill in the space between those framework tones. Some of those "6" degrees will be flatter in the minor mode, again emphasizing the labile nature of "imperfection." The curved arrows indicate where specific dissonances begin and then resolve to a more stable chord. These resolutions conclude on degrees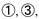 
or 
Note that the pattern of dissonances (and the exact type of dissonant chord, though unspecified in the diagram) is different when the bass rises or falls. So the up-or-down contour of the bass, the particular scale degrees of the bass, the resolution of dissonance, and the perfect/imperfect distinction between "5" and "6" chords are all connected by the Rule of the Octave. An adult composer’s knowledge of eighteenth-century composition would have involved more than the Rule of the Octave, but as a summary of the default harmonizations of stepwise basses it comes very close to capturing the norms of that musical repertory. The Rule of the Octave demonstrates that most chords do not have essential meanings. That is, abstractions like “IV” or “Subdominant” suppose an essential meaning to a triad on the fourth scale degree, when the historical fact was that the default sonorities on the fourth scale degree were not triads and depended on the direction of motion in the bass.
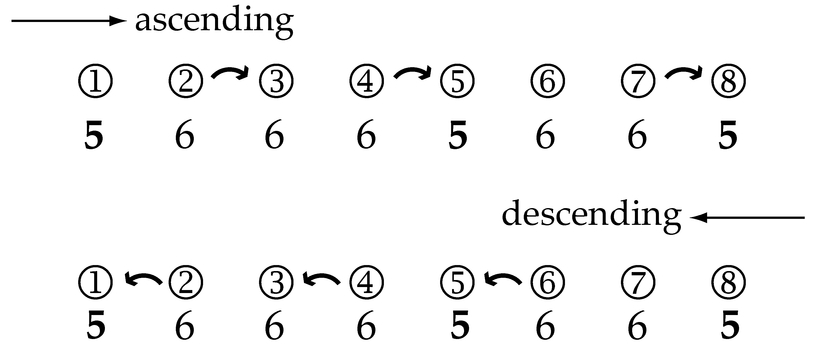
Figure 13.3 Rule of the Octave.
In the European classical tradition, the status of music as a language has long been a subject of debate. On the negative side, music rarely involves denotation, so music lacks truth values and a secure communication of agent, topic, or aspect. One might conceivably say, “Oh, that trill in the flute is about birdsong,” but saying that a Bach fugue in D major is about the Lutheran concept of grace would be extremely difficult to substantiate. Similarly, Umberto Eco once quipped that the sine qua non of a semiotic system is the ability to tell a lie (Eco, 1976, p. 7). Whatever sonatas may do, they do not lie. One might point to a “deceptive” cadence, but the substitution of an unexpected chord for an expected one is no more a lie than would be slipping on a banana peel.
On the positive side, music does share a number of other features of language. The linguist Talmy Givón (2001, pp. 7–13) has described the structure of human language as a three-level, non-uniform hierarchy. At the lower level words code semantic content; at the middle level clauses code propositional information; and at the upper level multi-propositional structures code discourse coherence. Givòn describes this hierarchy as non-uniform because each level depends on different types of entities and relationships. Supporting this idea of hierarchy are the brain’s three functionally different types of memory: (1) a sensory store, (2) short-term or working memory, and (3) long-term memory (Baddeley, 2007).
The musical analogues of Givòn’s three levels are (1) tones, brief melodic motives, chords, and timbres, (2) musical phrases, sequences, and cadences, and (3) musical form, with the associated concepts of repetition, return, variation, digression, and so forth. Young musicians in the classical tradition learned all these many patterns and relationships through exercises intended to provide them with ready exemplars and practice in employing them in different musical contexts. In the 1600s such training began to move from apprenticeship in the home of a master musician to apprenticeship in special institutions called conservatories. In conservatories, the focus on exemplar-based learning and improvisation continued throughout the eighteenth and nineteenth centuries.
Paralleling the development of an exemplar-based pedagogy were various attempts to provide scientific or scientistic explanations for how music works. The great French composer Jean-Philippe Rameau (1683–1764), for example, attempted to describe music as Isaac Newton had described physics. Musical atoms, in the guise of 1/3/5 triads, were subject to laws of “motion” determined by consonance. The actual bass of a composition was held to be the variable appearance of a more “fundamental bass,” which represented the lowest tones or “roots” of the proposed triads. “Roman numeral analysis” (i.e., marking the scale degrees of the fundamental bass with Roman numerals) in the modern music classroom is a descendant of Rameau’s approach. That approach, however ingenious, could never be fully reconciled with the actual behaviors of musicians. In several of his publications Rameau attempted unsuccessfully to show how his theories could fully explain the Rule of the Octave (Christensen, 2010, pp. 27–28).
When he learned about overtones (late 1722), Rameau began to modify his theories, switching the presumed underlying cause of musical relationships from mathematics to physics, from numerical ratios of string lengths to overtones. This idea of a microcosm of tones within each musical note had a lasting effect on music theory, especially as developed by nineteenth-century writers with notions of the organic growth of acorns into oak trees, of single tones into great symphonies (Neff, 1993). As attractive as the science of physics and biology might be as a fund of analogies, music is a product of human culture, not nature. Given the similarities of music and language mentioned above, the proposition that the physics of tones determines musical relationships makes no more sense than the proposition that the same physics determines language. Physics, or more aptly psychophysics, does constrain the transmission of musical and linguistic communications, but psychophysics has little to do with their contents.
The theories just alluded to, Rameau’s included, are usually described as theories of harmony. The importance of harmony as a central concept of Romantic music-theoretical thought can hardly be overstated. Textbooks in harmony (Ger.: Harmonielehren ) were written to serve the same roles in colleges and universities as textbooks in geology or astronomy. A student took the course, read the text, passed the examination, and then moved on to the next subject. For this to work with a cultural product like music, one needed to ignore the diversity and historically contingent nature of musical artworks and focus instead on a single attribute or essence. Patterns of adjacent chords served that purpose.
Given the historical sketch of compositional training and practice presented here, a careful reader may note that there was little mention of patterns of adjacent triads. In fact “chords” and “harmony” were not even central concepts in music theory until the time of Rameau. Throughout the eighteenth and nineteenth centuries young professional musicians continued to study two-voice counterpoint, the construction of two-voice frameworks, and the handling of sonorities in contexts like the Rule of the Octave. The schism between the exemplar-based training of professional musical artisans and the textbook caricatures of college courses in harmony might seem like a harmless detail of pedagogical history. But the fact that most experimental work in the area of harmony mistakes the latter for the former means that the well-documented musical conceptualizations held by the creators and performers of the European classical tradition are generally not being considered in empirical studies of their music.
To give some specificity to this distinction, let us examine three cases, one simple, one more complex, and one very complex. For the simple case, consider Pachelbel’s Canon in D, which is readily available online. In terms of Roman numerals, Pachelbel’s first three chords are I–V–vi (triads of D major, A major, and B minor). To some, “harmonic theory” defines this sequence as a deceptive cadence, meaning that the third chord is unexpected. But in the historical tradition of music apprentices, this pattern and its continuation were explicitly taught, meaning that the third chord was fully expected. For a more complex case, refer back to Figure 13.2, the excerpt from Vivaldi. What is the nature of the musical relationships in that excerpt? Clearly a literal concept of temporal adjacency would not be adequate. There are more than 100 adjacent events in this passage, even through syntactically the passage presents only four core events followed by a cadence. The particular sonorities used by Vivaldi could have been replaced by other sonorities, but how would one determine whether a replacement was or was not “correct”? In Vivaldi’s style, acceptable substitute sonorities would avoid disturbing the two-voice framework in the melody and bass. Yet if the two-voice framework determines categories of chords, chord successions are more a byproduct of counterpoint than the origin of musical coherence. The same question, expressed differently, would ask: Why are Vivaldi’s melody and bass exactly as presented and not a random selection from different notes of those same chords? That single excerpt cannot answer the question, but a study of a large corpus of Vivaldi’s concertos (he wrote several hundred of them) would reveal that the two-voice framework of Figure 13.2 is an extremely common element of Vivaldi’s usage.
If a harmony textbook says that the subdominant chord (IV, the F-major chord at the beginning of the Vivaldi excerpt) “goes to” the dominant chord (V), why does Vivaldi not do that, and is the failure to do so an artistic statement or license? If we eschew imagined physical explanations, we are left with explanations based on human behavior and usage. Imagine a situation in language where we have an idiomatic phrase like “It cost an arm and a leg,” meaning “It was very expensive.” Is the idiom wrong? No, because it is sanctioned by usage. Similarly in Vivaldi, ideas about what chord “goes to” what chord are of little use when the idiom in question reflects a different high-frequency usage. Classical composers did not pick chords from a pile on their desks and then arrange them in pleasing sequences. They learned and then reproduced specific idioms with origins in two-voiced counterpoint, idioms that have been termed musical schemata (Gjerdingen, 1988). In Vivaldi’s case he was employing an idiomatic riposte to the previous passage. That riposte, recently named a Prinner (Gjerdingen, 2007, ch. 2), is one of the most common patterns in all of eighteenth-century music. A statistical study (Symons, 2012) on a corpus of 300 compositions from the conservatories in Naples has confirmed the prevalence of the Prinner schema; it was the second most common four-event pattern out of thousands of such patterns. Following the practice of some corpus grammarians in linguistics (Stefanowitsch & Gries, 2003), one can say “In the context of a Prinner, an initial IV goes to I 6 ” because usage is determined idiom by idiom. So-called construction grammarians in linguistics would go further and say that language is nothing but idioms or constructions (Goldberg, 2013). The same may be true of classical music.
For the most complex case of how “chord grammar” and the older traditions of musical understanding diverge, let us turn to the Romantic repertory. The extent to which schematic contrapuntal frameworks served as scaffoldings for highly complex musical expressions can be observed in a dramatic and emotionally charged passage from the G-Minor Ballade of Frédéric Chopin (1810–1849), his Op. 23. Figure 13.4 illustrates how, in the local key of E-flat major, one could construct Chopin’s amazing design from common schematic constituents.
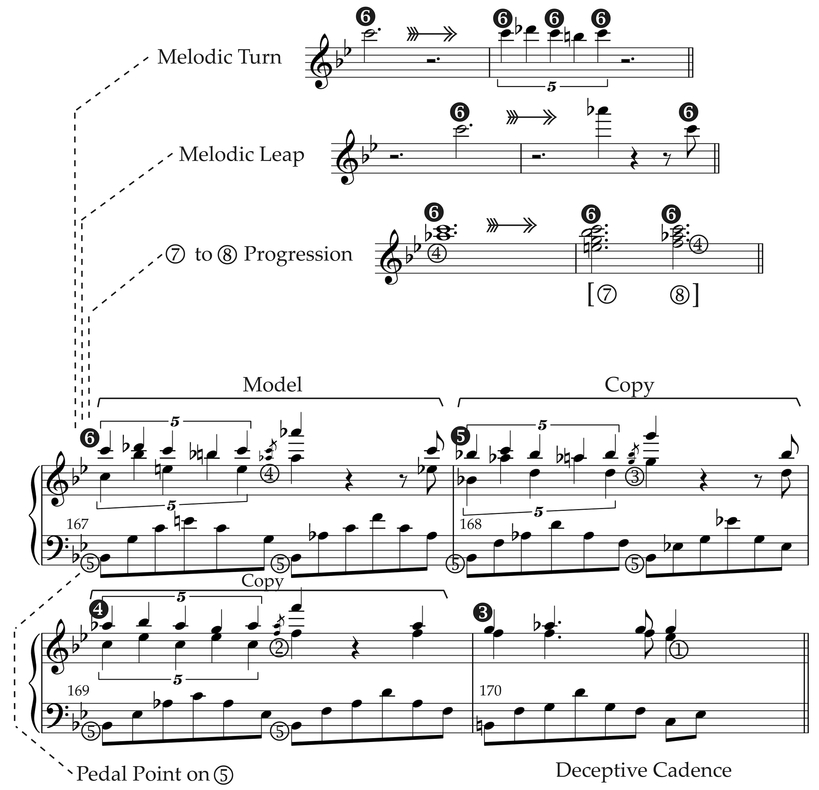
Figure 13.4 Frédéric Chopin, G-Minor Ballade Op. 23, mm. 167–170 with analysis.
In the terminology of construction grammar, the Prinner schema seen in the Vivaldi excerpt (Fig. 13.2) is the main and governing construction. Most obvious are the scale degrees 
in the melody, presented on the downbeats of successive measures just as with Vivaldi. The collocated bass, with scale degrees 
has a weaker presence in Chopin's actual passage, occurring in the lower tones of the right-hand part on the treble clef. It is contrapuntally shifted forward in time through the incorporation, at each of the four stages of the Prinner, of a smaller but historically important schema: a "1/3/5/6" chord moving to a 1/3/5 chord, as imperfection and dissonance resolving to perfection or as the ascent from 
to 
in the Rule of the Octave (e.g., in the upper tones of measure 167, Ε♯-G—B♭—C moving to F—A♭—C). That sense of instability resolving to stability is inherited by each stage of the governing schema. To this considerable level of complexity four further patterns are added. First, a low B♭ is placed in the bass as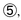 
a so-called "dominant pedal point" after the practice of organists holding an extended note on their pedalboard. Second, the expected concluding tone in the bass, E♭, is replaced by C, creating the well-known Deceptive Cadence. Third, a five-note melodic turn (e.g., C—D♭—C—B♯—D) is added to decorate each of the first three stages of the Prinner (note the turn's Β♯ clashing with the 1/3/5/6 chord's B♭ in measure 161). The upper tone of each turn is determined by the local key of that stage of the Prinner. So, the turn of measure 167 is oriented to F minor while the turn of measure 168 is oriented to E♭ major. Finally, as a fourth complication, the descending melodic leap from the high F♭ in measure 167 to the A♭5 and then in measure 168 to G5—a small schema known as a High-2 Drop (Gjerdingen, 2007, ch. 5) is added to the first three stages of the Prinner (i.e., to the model and its copies).
While Chopin’s passage represents breathtaking compositional skill coupled with pianis-tic virtuosity and artistic passion, it was not a wholly original combination. The linkage of several component patterns in the context of a large Prinner schema played over a dominant pedal was itself a traditional construction used for impressive moments in large compositions. Mozart frequently used it to set up the return of an opening theme (Ivanovitch, 2011), and it can be traced all the way back to the closing section of Pergolesi’s Stabat Mater (1736; see Gjerdingen, 2007, ch. 30). The student of harmony who might try to label the chords in this construction would most likely find the passage thoroughly baffling. Yet listeners familiar with the classical tradition find the passage quite lucid and moving because, due to frequent exposure, they have become familiar with all its component constructions and their typical musical meanings, all of which Chopin respects and exploits.
To sum up, the structure of European music in the classical tradition is based on the counterpoint of two-voice frameworks. In earlier centuries dense textures of many voices were woven together, with two-voice frameworks moving freely among the many voice pairs. From the eighteenth century onward, it became a norm for the melody and bass, the perceptually most salient voices, to present the two-voice framework while the inner voices took on subsidiary roles. Today the roles of “lead, rhythm, and bass” in popular ensembles are descendants of that classical division of labor. Melodies were fashioned by a technique called “diminution,” where the slower moving tones of a two-voice framework were replaced by faster moving decorative patterns. In over-learned schemata like cadences, the succession of sonorities could themselves become schematized, and it was this schematization of chordal successions that prompted several attempts to establish a syntax of harmony.
To essentialize harmony, however, is to mistake the moment-to-moment coloration of sonorities for the contrapuntally determined two-voice frameworks that defined the underlying musical syntax. How do we know such frameworks existed? We know because the pedagogical lessons and exercises used to teach the children apprenticed in conservatories have been recovered and republished (Gjerdingen, 2004, 2008). These lessons were arranged framework by framework. Some lessons tested the young apprentice’s ability to produce a given framework in different keys and meters. Others tested the apprentice’s ability to complete a series of frameworks when provided with only an upper or a lower voice.
Because these lessons forced the children (some of whom would later become great composers like Debussy and Ravel) to internalize these frameworks in both working and long-term memory, and because these frameworks have left obvious traces in the classical repertory of compositions, it is a fascinating yet empirically unanswered question if these regularities of pattern have also been internalized in twenty-first-century listeners with significant exposure to the classical repertory. In line with the many psycholinguistic studies of bilingualism in speech, a better understanding of the cognitive underpinnings of the classical tradition may provide a means of teasing out the effects of the other styles of music known to modern listeners. And finally, understanding the schematic nature of two-voice frameworks may provide a new way to study counterpoint, one of the least understood domains and most difficult areas to study in all of music cognition.
Givón, T. (2001). Syntax: An introduction (Vols. 1 & 2). Philadelphia, PA: John Benjamins Publishing Co.
Gjerdingen, R. O. (2007). Music in the galant style. New York, NY: Oxford University Press.
Huron, D. (1989). Voice denumerability in polyphonic music of homogeneous timbres. Music Perception, 6, 361–382.
Meyer, L., & Rosner, B. (1982). Melodic processes and the perception of music. In D. Deutsch (Ed.), The psychology of music (pp. 317–341). New York, NY: Academic Press.
Arnold, F. T. (1931). The art of accompaniment from a thorough-bass. Oxford: Oxford University Press.
Baddeley, A. D. (2007). Working memory, thought, and action. Oxford: Oxford University Press.
Bukofzer, M. (1935). The gymel, the earliest form of English polypony. Music and Letters, 16 (1), 77–84.
Burkholder, P. J., Grout, D. J., & Palisca, C. V. (2010). A history of Western music (8th ed.). New York, NY: Norton.
Christensen, T. (1992). The “règle de l’octave” in thorough-bass theory and practice. Acta Musicologica, 64 (2), 91–117.
Christensen, T. (2010). Thoroughbass as music theory. In D. Moelants (Ed.), Partimento and continuo playing in theory and practice (pp. 9–42). Leuven: Leuven University Press.
Cohen, D. (1971). Palestrina counterpoint—A musical expression of unexcited speech. Journal of Music Theory, 15, 84–111.
Eco, U. (1976). A theory of semiotics. Bloomington, IN: Indiana University Press.
Fuller, S. (1992). Tendencies and resolutions: The directed progression in “Ars Nova” music. Journal of Music Theory, 36, 229–258.
Gerbert, M. (Ed.). (1784). Scriptores ecclesiastici de musica sacra potissimum. St. Blasien.
Gjerdingen, R. O. (1988). A classic turn of phrase: Music and the psychology of convention. Philadelphia, PA: University of Pennsylvania Press.
Gjerdingen, R. O. (2004). Monuments of partimenti: A series presenting the great collections of instructional music intended for the training of European court musicians. Retrieved from: http://faculty-web.at.northwestern.edu/music/gjerdingen/partimenti/index.htm (last accessed 17 January 2017).
Gjerdingen, R. O. (2008). Monuments of solfeggi: A series presenting the great collections of instructional music intended for the training of European court musicians. Retrieved from: http://faculty-web.at.northwestern.edu/music/gjerdingen/solfeggi/index.htm (last accessed 18 January 2017).
Gjerdingen, R. O. (2014). “Historically informed” corpus studies. Music Perception, 31, 192–204.
Goldberg, A. (2013). Constructionist approaches. In T. Hoffman & G. Trousdale (Eds.), Oxford handbook of construction grammar (pp. 15–31). New York, NY: Oxford University Press.
Hiley, D. (1993). Western plainchant: A handbook. Oxford: Clarendon Press.
Holtmeier, L. (2007). Heinichen, Rameau, and the Italian thoroughbass tradition: Concepts of tonality and chord in the rule of the octave. Journal of Music Theory, 51, 5–49.
Ivanovitch, R. (2011). Mozart’s art of retransition. Music Analysis, 30 (1), 1–36.
Janin, B. (2012). Chanter sur le livre, Manuel pratique d’improvisation polyphonique de la Renaissance. Langres: Dominique Guéniot.
McClary, S. (2012). Desire and pleasure in seventeenth-century music. Los Angeles, CA: University of California Press.
Neff, S. (1993). Schoenberg and Goethe: Organicism and analysis. In C. Hatch and D. W. Bernstein (Eds.), Music theory and the exploration of the past (pp. 409–433). Chicago, IL: University of Chicago Press.
Stephanowitsch, A., & Gries, S. (2003). Collostructions: Investigating the interaction between words and constructions. International Journal of Corpus Linguistics, 8, 209–243.
Symons, J. (2012). Temporal regularity as a key to uncovering statistically significant schemas in an eighteenth-century corpus. Paper presented at the Society for Music Theory National Conference, New Orleans, LA.