 in the melody with
in the melody with  in the accompaniment. Wagner (2003) argues that this usage results from a combination of the minor pentatonic scale—widely used in the blues—with major-mode chords in the accompaniment.
in the accompaniment. Wagner (2003) argues that this usage results from a combination of the minor pentatonic scale—widely used in the blues—with major-mode chords in the accompaniment.David Temperley and Trevor de Clercq
Much of the research in music psychology has assumed the conceptual framework of “common-practice” music: Western art music of the 18th and 19th centuries. The questions asked often pertain most directly to the common-practice style—for example, questions about the perception of major and minor keys, classical harmonic progressions, and classical formal conventions—and stimuli are often drawn from this repertoire, or designed to imitate it. But in modern Western society, classical music is a relatively small part of the experience of most listeners. (This is especially true for younger listeners—e.g. college students—who provide the subject population for many music psychology experiments.) While it is certainly valid to study the perception and cognition of common-practice music, it also makes sense to explore other styles with which modern listeners may have greater familiarity.
In this chapter, we focus on melody and harmony in popular music, particularly rock. Recent work by a number of musicologists has contributed greatly to our understanding of harmony and melody in rock; in what follows, we survey this work. Nonetheless, there is to date no well-developed, widely accepted music-theoretical framework for rock as there is for common-practice music. Perhaps partly for this reason, the perception and cognition of rock music has also received little attention; psychological work on popular music has focused more on sociological issues, such as social identity (North & Hargreaves, 1999) and functions of music in everyday life (Sloboda, O’Neill, & Ivaldi, 2001). An important development has been the rise of corpus approaches to popular music (Bertin-Mahieux, Ellis, Whitman, & Lamere, 2011; Burgoyne, Wild, & Fujinaga, 2011), which can shed interesting light on issues of perception and cognition. In this chapter, we discuss our own statistical, corpus-based work on rock music, alongside other theoretical and empirical work as applicable.
Like many stylistic labels, “rock” resists precise definition. A sense of the common understanding of the term is provided by a recent survey by Rolling Stone magazine (2004), in which “rock musicians and other industry professionals” were asked to name the greatest songs of the “rock and roll era”; the results were compiled into a list of 500 songs. The top 10 songs of the list are shown in Table 14.1. It can be seen that the list includes a variety
Table 14.1 The top 10 songs from Rolling Stone magazine’s list of the “500 Greatest Songs of All Time” (2004).
| RANK | TITLE | YEAR | ARTIST |
| 1 | Like a Rolling Stone | 1965 | Bob Dylan |
| 2 | Satisfaction | 1965 | The Rolling Stones |
| 3 | Imagine | 1971 | John Lennon |
| 4 | What’s Going On | 1971 | Marvin Gaye |
| 5 | Respect | 1967 | Aretha Franklin |
| 6 | Good Vibrations | 1966 | The Beach Boys |
| 7 | Johnny B. Goode | 1958 | Chuck Berry |
| 8 | Hey Jude | 1968 | The Beatles |
| 9 | Smells Like Teen Spirit | 1991 | Nirvana |
| 10 | What’d I Say | 1959 | Ray Charles |
of sub-genres: 1950s rock and roll, “British Invasion” bands such as The Beatles and The Rolling Stones, soul and Motown, and 1990s alternative rock. A selection of 200 songs from the list provides the basis for the statistical corpus analysis that we discuss below. (Many of the details provided below are drawn from our earlier publications—de Clercq & Temperley, 2011, Temperley & de Clercq, 2013—although a significant portion of what follows also presents new findings.)
It is generally agreed that rock is "tonal" in the broad sense that every song has a tonal center—a pitch class that serves as a point of focus and stability (see Shanahan, this volume). Beyond this, however, there is little agreement as to the nature of tonality in rock. One controversial issue is the distinction between major and minor keys: while some scholars of rock label keys as major or minor, others have questioned the validity of this distinction (Stephenson, 2002; Covach, 1997), since some traditional markers of a "key"—such as the leading tone in minor—are not commonly found in rock. Another, related issue is the kinds of scales that are used in rock. Moore (1992, 1995, 2001) has emphasized the importance of diatonic modes in rock, citing Ionian (major), Mixolydian, Dorian, and Aeolian as especially common (see Figure 14.1). Pentatonic scales have also been widely discussed. Many rock melodies and chord progressions do not fit neatly into any conventional scale, however. For example, some songs, such as The Beatles' "Can't Buy Me Love," combine ♭ in the melody with
in the melody with  in the accompaniment. Wagner (2003) argues that this usage results from a combination of the minor pentatonic scale—widely used in the blues—with major-mode chords in the accompaniment.
in the accompaniment. Wagner (2003) argues that this usage results from a combination of the minor pentatonic scale—widely used in the blues—with major-mode chords in the accompaniment.
In our own research, we have explored scales in rock from a statistical perspective, using the Rolling Stone corpus discussed above. We transcribed the melodies of the 200 songs, and analyzed their harmony in Roman numeral notation (de Clercq & Temperley, 2011; Temperley & de Clercq,,2013). We then examined the distribution of scale-degrees (pitch-classes relative to the tonic) in both the melodies and the harmonic progressions. In examining the harmonic progressions, we took each chord to imply one instance of each scale-degree that it contained: for example, a I chord contains a 1, a 3, and a 5. In both the melodic and harmonic distributions, we found that the two least common scale-degrees Λ Λ . . were l>2 and Jf4, well below the other ten degrees in frequency; in the melodies, the value for b6 was also quite low. This suggests that there is^a "global" or "master" scale in rock, consisting of all the pitch-classes except b2 and $4, from which the scales of individual songs are drawn; elsewhere one of us has called this the "supermode" (Temperley, 2001). This does not mean that b2 and $4 are never used, but when they occur, they tend to have a surprising or destabilizing effect. Consider, for example, the striking bll chord at the end of the bridge in the Beatles' "Things We Said Today" (supporting the lyric "Love is here to stay and that 's enough"). Instead of the V chord that ended the previous phrase ("say that love is luck"), the bll facilitates a dramatic shift from the A major tonality of the bridge back to the A minor tonality of the verses,

Figure 14.1 Common scales used in rock (always assuming a tonal center of C).
To explore the scales used in individual songs, we used the method of statistical clustering. In this method, each song is represented by a scale-degree distribution; the distributions are then sorted into two categories or "clusters," such that songs with similar distributions are placed in the same category. We performed this process for both the melodic and harmonic datasets. For the melodies, the average distributions of the two clusters are shown in Figure 14.2. One cluster (CI) clearly represents the major scale: the seven major degrees have much higher values than the remaining five. Within the major scale, the five major pentatonic degrees ( , and
, and  ) have the highest values. The other cluster (C2) could roughly be described as "minor", in that
) have the highest values. The other cluster (C2) could roughly be described as "minor", in that  has a higher value than 3. In "classical" music in the minor mode,
has a higher value than 3. In "classical" music in the minor mode, 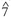 is more common than
is more common than 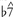 , and
, and  is more common than
is more common than 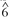 (Temperley, 2007b); in the rock "minor" distribution, however, the reverse is true in both cases. One could say the minor cluster implies Dorian mode
(Temperley, 2007b); in the rock "minor" distribution, however, the reverse is true in both cases. One could say the minor cluster implies Dorian mode 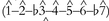 . Note also that
. Note also that  has a fairly high value in the rock minor distribution: adding
has a fairly high value in the rock minor distribution: adding  to the Dorian scale creates an eight-note scale,
to the Dorian scale creates an eight-note scale, 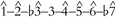 . We call this the "pentatonic union" scale, since it can be formed from the union of the major and minor pentatonic scales (see Figure 14.1). In almost 20% of melodies in the corpus, the eight degrees of this scale are more frequent than the remaining four.
. We call this the "pentatonic union" scale, since it can be formed from the union of the major and minor pentatonic scales (see Figure 14.1). In almost 20% of melodies in the corpus, the eight degrees of this scale are more frequent than the remaining four.
The same clustering process was applied to the harmonic distributions, and the results were similar, yielding “major” and “minor” clusters much like the ones generated from the melodic data. Interestingly, however, a substantial number of songs (over 20%) were in the minor melodic cluster but the major harmonic cluster. This captures the fact—noted earlier— that many rock songs employ  in the melody but
in the melody but  in the harmony. Altogether, then, our results give support for some kind of major/minor distinction in rock, but one which is rather different from the classical major/minor system. In particular, the rock minor system privileges
in the harmony. Altogether, then, our results give support for some kind of major/minor distinction in rock, but one which is rather different from the classical major/minor system. In particular, the rock minor system privileges  and
and  over
over  and
and  , and there is a high degree of "mixture" of
, and there is a high degree of "mixture" of 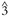 and
and  both in rock melodies and between melodies and the accompanying harmonies. This suggests that the major-minor dichotomy in rock is more of a continuum than a hard-and-fast distinction; in many cases, such as "Can't Buy Me Love," it is difficult to know which label to apply.
both in rock melodies and between melodies and the accompanying harmonies. This suggests that the major-minor dichotomy in rock is more of a continuum than a hard-and-fast distinction; in many cases, such as "Can't Buy Me Love," it is difficult to know which label to apply.
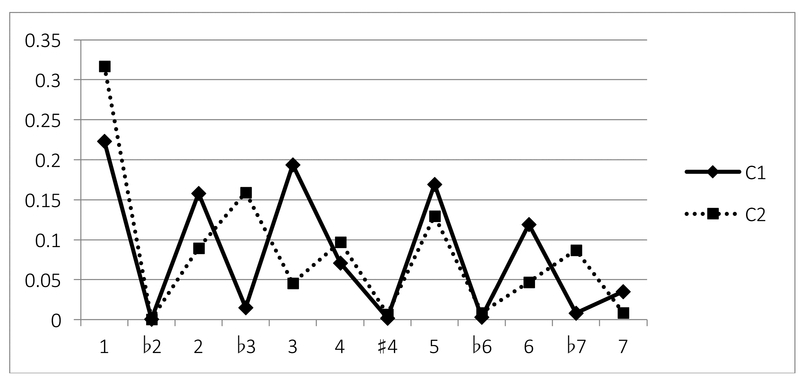
Figure 14.2 Scale-degree distributions from cluster analysis of melodies in the Rolling Stone corpus.
Have these patterns of scale-degree distributions in rock changed over time? Analysis of our corpus data suggests that, by and large, they have not. There is, however, one striking and curious exception: the use of 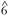 and
and  in "minor" melodies, which we define here as those in which
in "minor" melodies, which we define here as those in which  is more common than
is more common than  The
The 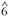 degree was more frequent than
degree was more frequent than  in more than 90% of minor melodies before 1980, but in less than half of minor melodies after that date. Our analyses of some songs since 2000, using another Rolling Stone list, suggests that the predominance of
in more than 90% of minor melodies before 1980, but in less than half of minor melodies after that date. Our analyses of some songs since 2000, using another Rolling Stone list, suggests that the predominance of  in minor songs has become even more pronounced in recent years (Temperley, Waller, & de Clercq, 2015). It appears that the Dorian or "pentatonic union" orientation of early "minor" rock has evolved toward something more like an Aeolian (natural minor) orientation.
in minor songs has become even more pronounced in recent years (Temperley, Waller, & de Clercq, 2015). It appears that the Dorian or "pentatonic union" orientation of early "minor" rock has evolved toward something more like an Aeolian (natural minor) orientation.
Scales can have strong emotional connotations; in common-practice music, the positive and negative associations of major and minor, respectively, are well-known. One might wonder about the expressive implications of the various scales used in rock. Temperley and Tan (2013) undertook a partial exploration of this issue by examining the emotional connotations of diatonic modes: listeners heard melodies in different modes and judged how “happy” they were. A strong pattern emerged, in which modes seemed less happy as scale-degrees were lowered: Ionian > Mixolydian > Dorian > Aeolian > Phrygian. (The exception was Lydian, which was less happy than Ionian, though it has a raised scale-degree— .) If one arranges the modes on the “line of fifths,” the circle of fifths stretched out into a line (assuming a constant tonic), it appears that scales get less happy as they move in the flat direction. This principle plays an important role in the emotional connotations of rock songs, and shifts of scale within songs (Temperley, 2013). It may also account for the practice of heavy metal, in which Phrygian mode is widely used, often coupled with extremely negatively charged lyrics (Walser, 1993; Biamonte, 2010).
.) If one arranges the modes on the “line of fifths,” the circle of fifths stretched out into a line (assuming a constant tonic), it appears that scales get less happy as they move in the flat direction. This principle plays an important role in the emotional connotations of rock songs, and shifts of scale within songs (Temperley, 2013). It may also account for the practice of heavy metal, in which Phrygian mode is widely used, often coupled with extremely negatively charged lyrics (Walser, 1993; Biamonte, 2010).
Related to scales is the issue of key identification in rock; here we define the "key" of a song as its tonal center, without specifying major or minor. Research on key-finding in common-practice music suggests that it depends largely on the distribution of pitch-classes in the piece; this is matched to an ideal distribution or "key-profile" for each key and the key is chosen that yields the best match (Krumhansl, 1990). We experimented with this and other approaches to key-finding in rock, using the Rolling Stone corpus. We found that, indeed, scale-degree distribution is a valuable indicator of key in this repertoire. The role of scale-degree distribution in key-finding can be reduced to three factors. First, there is a preference for an interpretation that remains within the "supermode"—avoiding  and
and 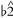 . For example, if a song contains a repeated chord progression F major—G major, we will tend not to hear it as being in F, since the G major chord contains a Β which is
. For example, if a song contains a repeated chord progression F major—G major, we will tend not to hear it as being in F, since the G major chord contains a Β which is  of F. Second, within the supermode, we tend to favor major mode: that is, if a song uses the C major scale, we will prefer a tonal center of C, though other tonics such as G, D, and A are possible. And, third, we favor an interpretation such that the most emphasized tones in the melody are tonic-triad degrees
of F. Second, within the supermode, we tend to favor major mode: that is, if a song uses the C major scale, we will prefer a tonal center of C, though other tonics such as G, D, and A are possible. And, third, we favor an interpretation such that the most emphasized tones in the melody are tonic-triad degrees 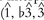 , and
, and  ).
).
While scale-degree distribution is important in key-finding, it proves not to be the only factor. Consider these two harmonic progressions (all major triads; vertical bars represent barlines):
| F Bb | F C | C F | Bb F |
The first appears in Bruce Springsteen’s “Rosalita,” the second in the Romantics’ “That’s What I Like About You” (transposed here for ease of comparison). The two patterns use exactly the same harmonies in the same sequence (imagine them repeating many times); yet, the tonal center seems to be F in the first case, but C in the second. We propose that this is due to the interaction of meter with the chords, specifically the placement of the chord progression relative to the two-bar “hypermeasures.” The change in tonal emphasis is a result of the hypermetrical placement of the harmonies: we prefer a tonal interpretation that locates the tonic harmony in a metrically strong position. Combining this rhythmic factor with melodic scale-degree distribution, we created a key-finding algorithm that matched human judgments of key in 97% of songs.
A large proportion of rock songs (83% in our corpus) remain in one key all the way through. With regard to modulating songs, a few general patterns can be noted. Many songs establish one tonal center in the verse and another in the chorus (de Clercq, 2012). A particularly common pattern is for a song to establish a minor orientation in the verse and then a major one in the chorus, maintaining the same diatonic scale but shifting tonal center (as in Neil Young’s “Keep on Rockin’ in the Free World”). Other songs, such as Duran Duran’s “Rio,” perform a similar minor-to-major shift by maintaining the same tonal center but altering the scale. While some tonal moves (such as minor to relative major) are especially common, instances of almost every possible modulation can be found; see Doll (2011) for examples. Frequently, modulations in rock seem to have an expressive motivation; an example is The Beatles’ “Penny Lane.” In this song, the verse, a nostalgic flashback to the narrator’s old neighborhood, contrasts with the chorus, depicting his current situation under “blue suburban skies”; the song mirrors this contrast tonally, modulating down a whole step for the chorus (from B to A).
Harmony in rock has been the subject of considerable discussion. Two influential and contrasting viewpoints are those of Everett (2008) and Stephenson (2002). Everett sees rock harmony as grounded in the norms of classical tonality. He argues that the basic I—V—I progression of common-practice music is often implied in rock even when it is not literally present. Progressions that violate classical harmonic norms, such as ♭VII—IV—I, are usually viewed as being not truly harmonic, but rather contrapuntal in origin. By contrast, Stephenson sees the logic of rock harmony as being fundamentally different from that of classical music. The normative root motions of rock music, in his view, are opposite to those of classical music: that is, ascending fifths and thirds, rather than descending fifths and thirds. While both authors recognize the diversity of rock harmony—Everett notes songs that deviate from classical norms, and Stephenson notes songs that adhere to them—there is clearly a marked difference in perspective here.

Figure 14.3 Harmonic motions between I, IV, and V in the Rolling Stone corpus.
We examined rock harmony from a statistical viewpoint, using our harmonic analyses of the Rolling Stone corpus. We again began by examining the overall distribution of roots—the primary note of a chord, which determines its function—in the corpus. Not surprisingly, I was the most common root (33% of all chord tokens in the corpus), followed by IV (23%), V (17%), ♭VII (7%), and VI (6%). This already indicates a contrast with classical music, in which V is much more common than IV (for data on common-practice harmony, see Tem-perley, 2009). We also examined the frequencies of transitions from one chord to another. IV is the most common chord to precede I, and also the most common chord to follow it; V is second-most common in both cases. It is instructive to examine the motions between these three chords; see Figure 14.3. Whereas in classical harmony, moves from IV to V are far more common than the reverse, in rock, V is almost as likely to move to IV as IV is to move to V. (The popularity of the first of these motions, V to IV, may stem from its occurrence in the standard 12-bar blues progression: I–I–I–I–IV–IV–I–I–V–IV–I.) Note also that IV and V are about equally likely to move to I; however, I is much more likely to move to IV than to V. In general, it seems that the directional asymmetries of classical harmony—where a move between two chords may be much more common than the reverse move—are largely absent in rock.
We also examined the frequency of different root motions categorized by interval; the results are shown in Table 14.2. Classical theory privileges root motion by descending fifth (-P5), descending third (-m3/-M3), and ascending second (+m2/+M2); if Stephenson is correct that rock norms are “opposite” to classical ones, we would expect the opposite motions (ascending fifth, ascending third, descending second). Our data suggests that the “classical” moves are more common than the “opposite” ones, but only slightly; ascending and descending forms of each interval are roughly equally common. The root motions in Table 14.2 are arranged on the “line of fifths”: a major second is two fifths (e.g. C–G–D), and so on. This reveals a very consistent pattern: root motions decline in frequency as line-of-fifths distance increases. In short, rock harmony shows no strong tendency either to adhere to classical harmonic norms or to go against them, but it does show a strong preference for motion by fifths, and more generally, motions that are “close” on the line of fifths.
At a larger scale, too, the norms of common-practice harmony seem to have little relevance to rock. In particular, there is no obligatory closing gesture—or “cadence”—analogous to the V–I cadence in classical music. However, a significant number of the songs in our corpus do have harmonic patterns that could be considered cadential. Temperley (2011) has suggested that a useful definition of “cadence” in a rock context is a harmonic gesture that moves to I at the end of the chorus, coinciding with the end of the vocal line (compare with Gjerdingen, this volume). Choruses ending with cadences create a sense of arrival and closure; those that do not project instability and motion (or, perhaps, stasis) into the following verse. By this definition, slightly more than half of songs in the Rolling Stone corpus (59%) have cadences; by far the most common chords preceding the tonic in these cadential gestures are V and IV. Among the songs that do not have cadences, the chorus either does not end on tonic harmony (AC/DC’s “Back in Black” is an example), or else settles on tonic harmony well before the end of the vocal line (as in Creedence Clearwater Revival’s “Proud Mary”).
Table 14.2 Root motions in the Rolling Stone corpus as proportions of the total, shown on the “line of fifths.”

Certain harmonic patterns in rock occur with particular frequency. In the early years of rock, the "12-bar blues progression (presented above) was predominant; many songs from the 1950s consist entirely of repetitions of this pattern, such as Elvis Presley's "Hound Dog." The popularity of the blues progression declined in later decades, but variants of it can still be seen: Bruce Springsteen's "Cover Me" could be regarded as a (minor) blues pattern, except using bVI— bVII—i instead of the V—IV—I progression. The late 1950s and early 1960s saw the rise of the "doo-wop" progression, I—vi—IV—V; innumerable songs of the period were built on this pattern (for some data, see Everett, 2009, p. 220). Over the next three decades, no single progression seems to have enjoyed such a central role. In recent years, however (since 2000), the progression I–V–vi–IV has become extremely widespread; an interesting feature of this pattern is that it occurs frequently in different rotations, often starting on vi and sometimes even on IV or V.
A controversial issue in the analysis of rock harmony is the validity of a reductive or "Schenkerian" approach, in which events (notes and chords) elaborate other events in a hierarchical manner. Such an approach entails a distinction between chords that are truly harmonic and those that are merely contrapuntal (linear) elaborations of other chords. While a number of scholars have applied the Schenkerian approach to rock (Wagner, 2003; Burns, 2005; Everett, 2008), others have expressed skepticism about its applicability (Middleton, 1990; Moore, 1995). It is difficult to resolve this issue using experimental or corpus methods. There is general agreement that at least some harmonic progressions in rock are best explained linearly, emerging as the result of melodic or bass lines: an example is the verse progression of the Eagles' "Hotel California," i—V— ♭VII—IV— ♭VI— ♭III—iv—V, in which the first six chords are clearly based on a descending chromatic line, 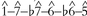 . In other cases, the Validity of a linear/hierarchical approach is less obvious, and even advocates of such analytic approaches often disagree as to how some progressions should be analyzed. A case in point is the common progression V—IV—I: Everett (2004) analyzes the IV in this progression as an interpolation between V and I, while Spicer (2005) argues that the V chord elaborates IV Another example is the progression ♭VII—IV—I; in this case,Everett (2008) analyzes the ♭VII as a contrapuntal elaboration of IV, while Doll (2009) suggests that IV is elaborative. Again, such judgments are subjective and it is hard to see how they can be resolved empirically.
. In other cases, the Validity of a linear/hierarchical approach is less obvious, and even advocates of such analytic approaches often disagree as to how some progressions should be analyzed. A case in point is the common progression V—IV—I: Everett (2004) analyzes the IV in this progression as an interpolation between V and I, while Spicer (2005) argues that the V chord elaborates IV Another example is the progression ♭VII—IV—I; in this case,Everett (2008) analyzes the ♭VII as a contrapuntal elaboration of IV, while Doll (2009) suggests that IV is elaborative. Again, such judgments are subjective and it is hard to see how they can be resolved empirically.
There has been very little experimental work focusing directly on rock harmony (or indeed rock music in general). One relevant study by Craton et al. (2016) examined nonmusician listeners'judgments of liking and surprise for major, minor, and dominant chords, given a major-mode context. They found that the: chords eliciting high liking ratings included some that are uncommon in (major-mode) classical music but common in rock, such as ♭VII and ♭III. This suggests—not too surprisingly—that listeners' perception of harmony may be affected by rock music—or, possibly, that rock music takes more advantage than does classical music of innate perceptual preferences for certain harmonic relationships. Clearly, there is much room for further research in this area.
We now turn our attention to melody. One issue—the set of scale-degrees from which a melody is drawn—has already been addressed. In this section we consider several other topics relating to the pitch organization of melody.
An interesting aspect of rock melody is its relationship with harmonic structure. In classical music, melodies are generally strongly constrained by the underlying harmony: melodic notes are either part of the underlying chord, or else are non-chord-tones that almost always “resolve” by step to another pitch (cf. Shanahan, this volume, on “anchoring”). In rock, however, Moore (1995) has argued that there is a kind of melodic–harmonic “divorce” that frees rock melody from its dependence on the accompanying harmony. Examining this situation more closely, Temperley (2007a) finds that, indeed, there are many cases in which the notes of a melody are neither chord-tones nor stepwise-resolving non-chord-tones. Temperley argues that this situation is especially common when the melody is pentatonic, and occurs more in verses than in choruses: In many songs, melody and harmony seem only loosely connected in the verse, but come together more tightly in the chorus. Nobile (2015) explores this phenomenon further, finding that it occurs in several different types of situations. In some cases of melodic–harmonic divorce, both the melody and harmony essentially prolong the same underlying harmony (usually tonic), but the accompaniment contains elaborating chords that momentarily clash with the melody. In other cases, the accompaniment “loops” over a simple repeated progression that may be truly independent of the melody.
Another distinctive feature of rock melody^is the mixing of 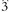 and
and 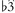 within a melodic line. This is of interest since, as noted earlier,
within a melodic line. This is of interest since, as noted earlier,  and
and  are not combined within anv conventional scale. In such situations, the factors governing the choice between
are not combined within anv conventional scale. In such situations, the factors governing the choice between 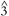 and
and 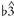 at particular moments prove quite complex. Sometimes the choice of pitch is guided by the harmony: In the verse of the Who's "I Can See For Miles,"
at particular moments prove quite complex. Sometimes the choice of pitch is guided by the harmony: In the verse of the Who's "I Can See For Miles,"  is used over a major I triad followed by
is used over a major I triad followed by 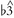 over a
over a 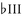 triad, hewing to the harmony in both cases, Harmony is not the only influential factor, however. Consider the first phrase of the Jackson Five's "ABC"— "You went to school te learnt, girl / things you never, never knew before": The melody features
triad, hewing to the harmony in both cases, Harmony is not the only influential factor, however. Consider the first phrase of the Jackson Five's "ABC"— "You went to school te learnt, girl / things you never, never knew before": The melody features  at "went" but
at "went" but 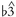 at "never never." The determining factor here seems to be the fact that the first half of the line gravitates around
at "never never." The determining factor here seems to be the fact that the first half of the line gravitates around  , and the second half around 1; in general,
, and the second half around 1; in general,  tends to be used in proximity to
tends to be used in proximity to  , and
, and 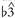 in proximity to
in proximity to  . There is also a tendency to use
. There is also a tendency to use  rather than
rather than  at cadential points. In the chorus of Crosby, Stills, Nash, and Youngs "Woodstock",
at cadential points. In the chorus of Crosby, Stills, Nash, and Youngs "Woodstock", 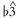 is used throughout the chorus but shifts to
is used throughout the chorus but shifts to  on the final word, coinciding with the cadential move to tonic: "And we've got to get ourselves back to the gar-den." Choices between
on the final word, coinciding with the cadential move to tonic: "And we've got to get ourselves back to the gar-den." Choices between  and
and  may also be influenced by expressive considerations; in "Woodstock," the shift to
may also be influenced by expressive considerations; in "Woodstock," the shift to 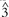 at the end of the chorus perhaps represents the triumphant return to the "garden."
at the end of the chorus perhaps represents the triumphant return to the "garden."
Most rock melodies contain a large amount of melodic repetition. This repetition may be exact, but more often it involves variation and elaboration. For example, in the first verse of Marvin Gaye’s “I Heard it through the Grapevine,” the first and third phrases (“I bet you wonder how I knew / With some other guy you knew before”) are clearly related, but neither the pitches nor the rhythms are identical—the same with the second and fourth phrases. Many successful songs feature repetition at different temporal levels. In Avril Lavigne’s “Complicated,” we find a repeated one-measure pattern in the verse, a half-measure pattern in the pre-chorus, and a two-measure pattern in the chorus. This complex repetition structure helps to maintain the listener’s interest. There is also, of course, larger-scale repetition of entire sections; this gets into the topic of form, which is beyond our scope here (see Covach, 2005; de Clercq, 2012).
The rhythmic aspects of a rock song must be understood in relation to its meter. Rock employs conventional metrical frameworks similar to those in common-practice music and many other Western styles; the vast majority of songs are in 4/4. Whereas the inference of meter in common-practice music is a complex process, in rock the meter is usually conveyed quite unambiguously by the drum pattern, which typically marks stronger beats of the measure (normally beats 1 and 3) with the kick drum and weaker beats (beats 2 and 4) with the snare.
Because the meter is expressed so clearly by the drums, the vocals—and to some extent the other instruments as well—need not constantly reinforce it and may indeed play against it with considerable freedom. This is clearly reflected in our corpus. Figure 14.4 shows the distribution of note-onsets across positions in the measure, for a corpus of European folk melodies (Schaffrath, 1995) and also for the melodies in the Rolling Stone corpus. (In both cases, we included only melodies in 4/4 that contain some notes on weak eighth-note beats but no notes on lower-level beats.) The folk melodies align strongly with the metrical framework, with the most notes occurring on strong quarter-note beats (positions 1 and 5), somewhat fewer notes on weak quarter-note beats (3 and 7), and still fewer on weak eighth-note beats. By contrast, in the rock corpus, the frequency of onsets is roughly uniform across the eight positions. With regard to the distribution of onsets, then, rock melodies would appear to conflict with the underlying meter almost as much as they support it.
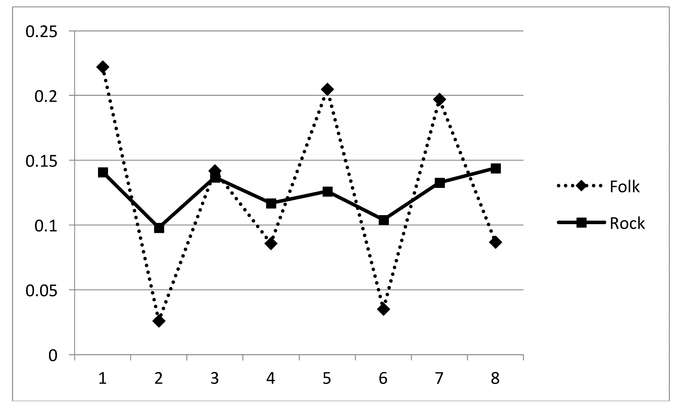
Figure 14.4 Distribution of events across positions of the 4/4 measure in European folk songs (the Essen Folksong Collection; Schaffrath, 1995), and rock songs (the Rolling Stone corpus).
This is not to say, however, that rock melodies are completely unconstrained by the meter. An important phenomenon here is anticipatory syncopation: accented events, such as stressed syllables, long notes, and changes of harmony, often occur on a beat just before a metrically strong beat. In such cases, they are understood as “belonging” on the following strong beat. Sometimes, unstressed syllables next to stressed ones are also understood as anticipatory. Michael Jackson’s “Billie Jean” is illustrative (see Figure 14.5A). The phrase “beauty queen” seems on the surface to conflict with the meter, since the unstressed syllable “-ty” falls on the downbeat. But if the phrase is shifted to the right by one eighth-note, as shown in the figure, the text and the meter line up perfectly: the main stress of the phrase “beau-” falls on the downbeat, the secondary stress “queen” on a weak quarter-note beat, and the unstressed “-ty” on an weak eighth-note beat. (It is perhaps significant that the metrical position with the most onsets in the rock data in Figure 14.4 is the last eighth-note beat of the measure; this may partly reflect syncopated events anticipating the following downbeat.) Later in the song, the phrase “people always told me” (Figure 14.5B) reflects a more complex pattern of syncopation. One could understand it as implying the underlying rhythm shown in the figure (in which “al-” is syncopated by a sixteenth-note, “told” by an eighth-note, and “me” by a dotted eighth). At the same time, the surface rhythm also creates a cross-rhythm, with dotted-eighth intervals between the stressed syllables “peo-,” “al-,” “told,” and “me”; such cross-rhythms are common in rock (Traut, 2005).


Figure 14.5 Two phrases from Michael Jackson’s “Billie Jean,” showing anticipatory syncopations.
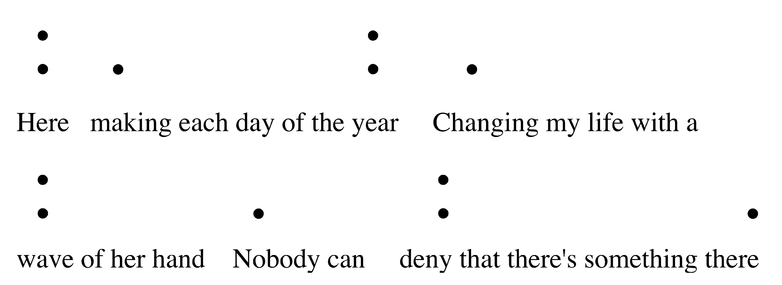
Figure 14.6 The Beatles, “Here, There, and Everywhere,” showing phrases and hypermeter. (Double dots indicate strong measures; single dots indicate weak measures.)
Also important is the alignment between melodic phrases and hypermeter (meter at a higher level). We may distinguish between beginning-accented phrases, in which the strongest beat in the phrase occurs near the beginning, and end-accented phrases, in which the strongest beat occurs at or near the end. Some songs maintain one kind of structure or another throughout, while others mix the two. The Beatles’ “Here, There, and Everywhere” is a case of the latter kind (Figure 14.6). After the first, very short phrase—just a single syllable—the next phrase is end-accented, ending on (or just before) the third downbeat. (In general, odd-numbered measures are assumed to be stronger than even-numbered ones.) The third phrase is rhythmically parallel to the second, but is extended past the fifth downbeat, so that its strongest beat falls in the middle of the phrase. The next short phrase is beginning-accented, and a longer beginning-accented phrase follows. The variety of phrase accentuation, and also of phrase length, is partly what makes this melody engaging and satisfying.
A central concern of music psychology has been the exploration of tacit musical knowledge that listeners have acquired simply through exposure to music. While some of this knowledge may relate to musical phenomena that are universal or nearly so—for example, the preponderance of small melodic intervals (Huron, 2006)—much of it is style-specific. To date, little research in music psychology—at least, research using non-musician subjects—has focused on the styles of music with which such listeners are most familiar. In this chapter, we have put forth a number of concepts that we believe are important in rock melody and harmony, based on our own experience and intuitions, other authors' views, and corpus data. These include concepts of scale and key (such as the "supermode"), harmony (the prevalence of fifth motions and other "close" moves on the circle of fifths), melody (the complex interplay between 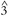 and
and  ), and rhythm (anticipatory syncopation). At present, we know very little about listeners' grasp of these concepts; this would seem to be a ripe area for exploration in experimental psychology. In addition, we hope this chapter has helped to demonstrate the great value of statistical corpus data in music research, both as a way of helping untangle disputed issues (such as the validity of the major/minor distinction) and as a source of new insights.
), and rhythm (anticipatory syncopation). At present, we know very little about listeners' grasp of these concepts; this would seem to be a ripe area for exploration in experimental psychology. In addition, we hope this chapter has helped to demonstrate the great value of statistical corpus data in music research, both as a way of helping untangle disputed issues (such as the validity of the major/minor distinction) and as a source of new insights.
de Clercq, T., & Temperley, D. (2011). A corpus analysis of rock harmony. Popular Music, 30, 47–70.
Everett, W. (2009). Foundations of rock. New York, NY: Oxford University Press.
Moore, A. (2001). Rock: The primary text. Aldershot, UK: Ashgate.
Stephenson, K. (2002). What to listen for in rock. New Haven, CT: Yale University Press.
Temperley, D., & de Clercq, T. (2013.) Statistical analysis of harmony and melody in rock music. Journal of New Music Research, 42, 187–204.
Bertin-Mahieux, T., Ellis, D., Whitman, B., & Lamere, P. (2011). The million song dataset. In A. Klapuri & C. Leider (Eds.), Proceedings of the 12th International Society for Music Information Retrieval Conference, Utrecht, Netherlands.
Biamonte, N. (2010). Modal and pentatonic patterns in rock music. Music Theory Spectrum, 32, 95–110.
Burgoyne, J., Wild, J., & Fujinaga, I. (2011). An expert ground truth set for audio chord recognition and music analysis. In A. Klapuri, & C. Leider (Eds.), Proceedings of the 12th International Society for Music Information Retrieval Conference, Miami, Florida.
Burns, L. (2005). Meaning in a popular song: The representation of masochistic desire in Sarah McLachlan’s “Ice.” In D. Stein (Ed.), Engaging music: Essays in musical analysis (pp. 136–148). New York, NY: Oxford University Press.
Covach, J. (1997). Progressive rock, “Close to the Edge”, and the boundaries of style. In J. Covach & G. M. Boone (Eds.), Understanding rock: Essays in musical analysis (pp. 3–31). New Y ork, NY: Oxford University Press.
Covach, J. (2005). Form in rock music: A primer. In D. Stein (Ed.), Engaging Music (pp. 65–76). New York, NY: Oxford University Press.
Craton, L., Juergens, D., Michalak, H., & Poireier, C. (2016). Roll over Beethoven? An initial investigation of listeners’ perception of chords used in rock music. Music Perception, 33, 332–343.
de Clercq, T. (2012). Sections and successions in successful songs: A prototype approach to form in rock music. PhD dissertation, Eastman School of Music.
Doll, C. (2009). Transformation in rock harmony: An explanatory strategy. Gamut, 2(1), 1–44. doi:10.7282/T31J9CD8
Doll, C. (2011). Rockin’ out: Expressive modulation in verse-chorus form. Music Theory Online, 17(3). www.mtosmt.org/issues/mto.11.17.3/mto.11.17.3.doll.html
Everett, W, (2004). Making sense of rock’s tonal systems. Music Theory Online, 10 (4). www.mtosmt.org/issues/mto.04.10.4/mto.04.10.4.w_everett.html
Everett, W. (2008). Pitch down the middle. In W. Everett (Ed.), Expression in pop-rock music (2nd ed.) (pp. 111–74). New York, NY: Routledge.
Hansen, C., & Hansen, R. (1988). How rock music videos can change what is seen when boy meets girl. Sex Roles, 19, 287–316.
Huron, D. (2006). Sweet anticipation: Music and the psychology of expectation. Cambridge, MA: MIT Press.
Krumhansl, C. (1990). Cognitive foundations of musical pitch. New York, NY: Oxford University Press.
Middleton, R. (1990). Studying popular music. Buckingham, UK: Open University Press.
Moore, A. (1992). Patterns of harmony. Popular Music, 11, 73–106.
Moore, A. (1995). The so-called “flattened seventh” in rock. Popular Music, 14, 185–201.
Nobile, D. (2015). Counterpoint in rock music: Unpacking the melodic-harmonic divorce. Music Theory Spectrum, 37, 189–203.
North, A., & Hargreaves, D. (1999). Music and adolescent identity. Music Education Research, 1, 75–92.
Rolling Stone. (2004). The 500 greatest songs of all time. Rolling Stone, 963, 65–165.
Schaffrath, H. (1995). The Essen Folksong Collection in the Humdrum kern format. D. Huron (Ed.). Menlo Park, CA: Center for Computer Assisted Research in the Humanities.
Sloboda, J., O’Neill, S., & Ivaldi, A. (2001). Functions of music in everyday life: An exploratory study using the experience sampling method. Musicae Scientiae, 5, 9–32.
Spicer, M. (2005). Review of Everett, The Beatles as musicians: The Quarry Men through Rubber Soul. Music Theory Online, 11(4). http://www.mtosmt.org/issues/mto.05.11.4/mto.05.11.4.spicer.html
Temperley, D. (2001). The cognition of basic musical structures. Cambridge, MA: MIT Press.
Temperley, D. (2007a). The melodic-harmonic “divorce” in rock. Popular Music, 26, 323–342.
Temperley, D. (2007b). Music and probability. Cambridge, MA: MIT Press.
Temperley, D. (2011). The cadential IV in rock. Music Theory Online, 17(1). http://www.mtosmt.org/issues/mto.11.17.1/mto.11.17.1.temperley.html
Temperley, D. (2012). Scalar shift in popular music. Music Theory Online, 17(4). www.mtosmt.org/ issues/mto.11.17.4/mto.11.17.4.temperley.html
Temperley, D. (2009). A statistical analysis of tonal harmony. www.theory.esm.rochester.edu/temperley/kp-stats
Temperley., D., & Tan, D. (2013). Emotional connotations of diatonic modes. Music Perception, 30, 237–57.
Temperley, D., Waller, A., & de Clercq, T. (2015). Changes in rock melody, 1954–2009. Paper presented at the Society for Music Perception and Cognition Annual Meeting, Nashville, TN.
Traut, D. (2005). “Simply Irresistible”: Recurring accent patterns as hooks in mainstream 1980s music. Popular Music, 24, 57–77.
Wagner, N. (2003). “Domestication” of blue notes in the Beatles’ songs. Music Theory Spectrum, 25, 353–365.
Walser, R. (1993). Running with the devil: Power, gender, and madness in heavy metal music. Hanover, NH: University Press of New England.