, so that p q means that p ∨ q = q (or, equivalently, that p ∧ q = p or that p → q = 1). The simple Boolean algebra {0, 1} is denoted by O.TERMS AND EQUALITY
PREDICATES, TERMS, OPERATIONS, AND EQUALITY IN POLYADIC BOOLEAN ALGEBRAS
The theory of Boolean algebras is an algebraic counterpart of the logical theory of the propositional calculus; similarly, the theory of polyadic (Boolean) algebras1 is an algebraic way of studying the first-order functional calculus. The Gödel completeness theorem, for instance, can be formulated in algebraic language as a representation theorem for a large class of simple polyadic algebras, together with the statement that every polyadic algebra is semisimple.2 The next desideratum is an algebraic study of the celebrated Gödel incompleteness theorem. Before that can be achieved, it is necessary to investigate the algebraic counterparts of some fundamental logical concepts (such as the ones mentioned in the title above). The purpose of this rather technical note is to report (without proofs) the results of such an investigation; the details are being published elsewhere.3
1. Basic Concepts.—For convenience of reference, this section contains the definitions of the (already known) basic concepts of algebraic logic; all further work is based on these concepts and on their elementary properties.
The following notation will be used for every Boolean algebra A : the supremum of two elements p and q of A is p ∨ q, the infimum of p and q is p ∧ q, the complement of p is p', the zero element of A is 0, and the unit element of A is 1. Sometimes it is convenient to write p → q instead of p' ∨ q. The natural order relation is denoted by , so that p q means that p ∨ q = q (or, equivalently, that p ∧ q = p or that p → q = 1). The simple Boolean algebra {0, 1} is denoted by O.
A quantifier (more precisely, an existential quantifier) on a Boolean algebra A is a mapping 
of A into itself such that (i) 0 = 0, (ii) p p, and (iii) (p ∧ q) = p ∧ q, for all p and q in A. Suppose that A is a Boolean algebra, I is a set, S is a mapping that associates a Boolean endomorphism S(τ) of A with every transformation τ from I into I, and is a mapping that associates a quantifier (J) on A with every subset J of I. The quadruple (A, I, S, ) is a polyadic algebra if (i) (ø) is the identity mapping on A (here ø is the empty set); (ii) (J ∪ K) = (J) (K) whenever J and K are subsets of I; (iii) S(δ) is the identity mapping on A (here δ is the identity transformation on I); (iv) S(στ) = S(σ) S(τ) whenever σ and τ are transformations on I; (v) S(σ) (J) = S(τ) (J) whenever σi = τi for all i in I – J; and (vi) (J) S(τ) = S(τ) τ−1J) whenever τ is a transformation that never maps two distinct elements of I onto the same element of the set J.
If I is a set, X is a non-empty set, and B is a Boolean algebra, the set of all functions from the Cartesian product XI into B is a Boolean algebra with respect to the obvious pointwise operations. If τ is a transformation on I, and if x and y are in
XI, write τ*x = y whenever yi = xTi for all i in I. (The value of a function x from I into X, i.e., of an element x of XI, at an element i of I will always be denoted by xi.) If p is a function from XI into B, write S(τ)p for the function defined by (S(τ)p) (x) = p(τ*x). If J is a subset of I and if x and y are in XI, write x J * y whenever xi = yi for all i in I – J. If p is a function from XI into B, and if the set {p(y): x J* y} has a supremum in B for each :x in XI, write (J)p for the function whose value at x is that supremum. A functional polyadic algebra is a Boolean subalgebra A of the algebra of all functions from XI into B, such that S(τ)p 
A whenever p A and τ is a transformation on I, and such that (J)p exists and belongs to A whenever p A and J is a subset of I. The set X is called the domain of this functional polyadic algebra.
It is convenient to be slightly elliptical and, instead of saying that (A, I, S, ) is a polyadic algebra, to say that A is a polyadic algebra, or, alternatively, to say that A is an I-algebra. An element of I is called a variable of the algebra A. The degree of A is the cardinal number of the set of its variables. An element p of A is independent of a subset J of I if (J)p = p; the set J is a support of p if p is independent of I – J. The algebra A is locally finite if each of its elements has a finite support. Some of the results that follow are true for arbitrary polyadic algebras, but most are not. To simplify the statements, it will be assumed throughout the sequel that (A, I, S, ) is a fixed, locally finite polyadic algebra of infinite degree.
Associated with every subset J of I there is a polyadic algebra (A−, I−, S−, −) that is said to be obtained from A by fixing the variables of J. The set A− is the same as the set A, and I− = I – J. If τ− is a transformation on I−, let τ be its canonical extension to I (i.e., τ is the extension of τ− to I such that τi = i whenever i J), and write S−(τ−)p = S(τ)p for every p in A. If J− is a subset of I−, then J− is also a subset of I; write − (J−)p = (J−)p for every p in A.
Suppose that c is a mapping that associates a Boolean endomorphism of A with every subset K of I; denote the value of c at iv by S(K/c). The mapping c is a constant of A if (i) S(ø/c) is the identity mapping on A; (ii) S(H ∪ K/c) = S(H/c) S(K/c), (iii) S(H/c) (K) = (K) S (H – K/c), and (iv) (H) S(K/c) = S(K/c) (H – K), whenever H and K are subsets of I; and (v) S(K/c) S(τ) = S(τ) S(τ−1K/c) whenever K is a subset of I and τ is a transformation on I. (The notation here is different from the one used before for constants; the innovation has a beneficial unifying effect.)
2. Predicates.—An n-place predicate of A (n = 1, 2, 3, . . .) is a function P from In into A such that if (i1, . . . , in) In and if τ is a transformation on I, then
THEOREM 1. If P is an n-place predicate of A and if (i1 . . ., in) in, then {i1 . . . , in) supports P(i1, .. ., in).
THEOREM 2. If p A and if j1 . . . , jn are distinct variables such that {j1, . . . , jn} supports p, then there exists a unique n-place predicate P of A such that P(j1,. . . , jn) = p
COROLLARY. Every element of A is in the range of some predicate of A.
Whereas, by Theorem 1.1, a value of a predicate depends on no more variables than the visible ones, it may happen that it depends on fewer. If, for example, Q is a 1-place predicate, and if P(i, j) = Q(i) for all i and j, then P is a 2-place predicate such that {i} supports P(i, j). It is interesting to ask what happens if the roles of P and Q in this discussion are interchanged. Suppose, in other words, that Q is a 2-place predicate and that j is a particular element of I, and write P(i) = Q(i, j) for all i. The function P is not quite a predicate; it is a {j}-predicate in the sense of the following definition. If J is a finite subset of I, and if A− is the algebra obtained from A by fixing the variables of J, then an n-place J-predicate of A is an n-place predicate of A−. What was called a predicate before is a ø-predicate in the present terminology.
THEOREM 3. If j1, . . . , jm are distinct elements of I, if J = {j1, . . . , jm}, and if P is an n-place J-predicate of A, then there exists a unique (n + m)-place predicate Q of A such that
whenever (i1 . . . , in) e (I – J)n.
It is easy to see that the construction described in Theorem 3.3 always does yield a J-predicate.
3. Terms.—Suppose that M and N are finite subsets of I. A transformation σ on I will be said to be of type (M, N) if
and
If J is a finite subset of I, and if A− is the algebra obtained from A by fixing the variables of J, then (by definition) a J-constant of A is a constant of A−. If c is J-constant, then S(K/c) is not defined for every subset K of I; this is the main point in which the concept of a J-term (to be defined next) differs from that of a J-constant. If J is a finite subset of I, a J-term is a mapping t that associates with every subset K of I a Boolean endomorphism of A, denoted by S(K/t), so that the restriction of t to the subsets of I – J is a J-constant of A, and so that if p is an element of A with finite support L, if K is a finite subset of I, and if σ is a transformation of type (K, L ∪ J), then S(K/t)p = S(σK/t) S(σ)p. Every constant is a ø-term (and hence a J-term for every finite set J). j I and if t is defined by writing S(K/t) = S(K/j) for every subset K of I, then t is a {j}-term. (The transformation (K/j) is the one that maps every element of K onto j and every element of I – K onto itself.) In this sense, the concept of a term is a simultaneous generalization of the concept of a constant and the concept of a variable.
THEOREM 4. If c is a J-constant, then there exists a unique J-term t such that S(K/t) = S(K/c) whenever K ⊂ I – J.
4. Properties of Terms.—The algebraic behavior of terms is similar to, but necessarily somewhat more complicated than, the algebraic behavior of constants. The chief complication arises in the relation between terms and transformations.
To get a concise statement of that relation, it is convenient to introduce a new-item of notation. If τ is a transformation on I and if J is a subset of I, then let τJ be the transformation such that τ.j = τ on τ−1J and τsJ = δ outside τ−1J.
THEOREM 5. If t is a J-term of A, if H and K are subsets of I, and if τ is a transformation such that τ = δ on J, then
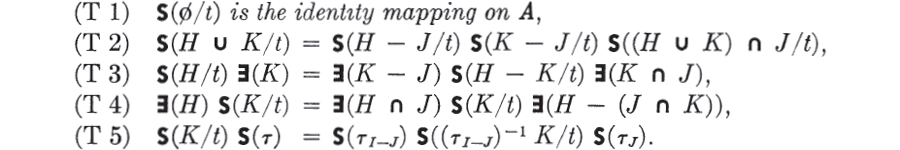
THEOREM 6. If t is a J-term, if K is a subset of I, and if p is an element of A with support L, then S(K/t)p = S(K ∩ L/t)p and S(K/t)p has support J ∪ (L – K).
The following result concerning terms is the deepest one; it is used repeatedly in the construction of terms satisfying various conditions.
THEOREM 7. If J and K are finite subsets of I, if i is a Boolean homomorphism from the range of (K) into A, and if i is an element of I – (J ∪ K) such that (i) (i) g(K) = g(K), (ii) g(K) (i) = (K) (i), (iii) g(K)(j) = (j) g(K) whenever j ≠ i and j I – J, and (iv) g(K) S(τ) = S(τ) g (K) whenever τ is a transformation that maps some finite subset of I – ({i} ∪ J ∪ K) into itself and is equal to δ otherwise, then there exists a J-term t of A such that S(i/t) (K) = g(K).
The next result shows that the term t of Theorem 7.7 is unique.
THEOREM 8. If J and K are finite subsets of I, if s and t are J-terms, and if i is an element of I – (J ∪ K) such that S(i/s)p = S(i/t)p whenever p is independent of K, then s = t.
A transformation on I acts in a natural way not only on the variables but also on the terms of A. If τ is a transformation and if t is a J-term, let τ0 be the transformation such that τ0 = τ on J and τ0 = δ outside J, and let i be an element of I – J; an application of Theorems 7 and 8 shows that there exists a unique τJ-term, to be denoted by τt, such that S(i/τt)p = S(τ0) S(i/t)p whenever p is independent of J. This definition of τt is unambiguous (i.e., it does not depend on the particular choice of i).
THEOREM 9. If t is a J-term, then δt = t; if σ and τ are transformations, then (στ)t = σ(τt); if σ = τ on J, then σt = τt.
If P is an n-place predicate and if t1 . . . , tn are terms, then there is a natural way of defining P(t1 . . . , tn). To do so, suppose that t1 is a J1-term, . . . , tn is a Jn-term, let i1 . . . , in be distinct elements of I – (J1 ∪ . . . ∪ Jn), and write
This definition of P(t1 . . . , tn) is unambiguous (i.e., it does not depend on the particular choice of i1, . . . , in).
THEOREM 10. If P is an n-place predicate, if t1, . . . , tn are terms, and if τ is a transformation, then
5. Operations.—An n-place operation (n = 1, 2, 3, . . .) of A is a function T on In whose values are terms of A, such that if (i1, . . . , in) e In and if τ is a transformation on I, then
The theory of operations is quite similar to the theory of predicates. All the results of Section 2 have their operation analogues; the following result, for example, is the analogue of Theorem 1.1.
THEOREM 11. If T is an n-place operation of A and if (i1, . . . , in) In, then T(i1, . . . , in) is an {i1 . . . , in)-term.
The useful part of the theory of operations is based on the fact that there is a natural sense in which the variables of a term can be replaced by terms. (In this rough, descriptive language, the theory of transforms of terms furnishes a natural sense in which the variables of a term can be replaced by other variables.) If s isan H-term, t is a J-term, and K is a subset of I, let i be an element of I – (H ∪ J); an application of Theorems 7 and 8 shows that there is a unique (H ∪ (J – K))-term, to be denoted by (K/s)t, such that S(i/(K/s)t)p = S(J ∩ K/s) S(i/t)p whenever p is independent of J. This definition of (K/s)t is unambiguous.
If T is an n-place operation and if t1 . . . , tn are terms, then there is a natural way of defining T(t1, . . . , tn). To do so, suppose that t1 is a J1-term, . . . , tn is a Jn-term, let i1 . . . , in be distinct elements of I – (J1 ∪ . . . ∪ Jn), and write
This definition of T(t1 . . . , tn) is unambiguous.
THEOREM 12. If T is an n-place operation, if t1 . . . , tn are terms, and if τ is a transformation, then
6. Equality.—An equality for A is a 2-place predicate E that is reflexive (i.e., E(i, i) = 1 for all i) and substitutive (i.e., p ∧ E(i, j) = S(i/j)p ∧ E(i, j) for all i and j and for all p in A). (The transformation (i/j) is the one that maps i onto j and everything else onto itself.) An equality E is necessarily symmetric (i.e., E(i, j) = E(j, i) for all i and j) and transitive (i.e., E(i, j) ∧ E(j, k) E(i, k) for all i, j, and k). If E is an equality for A, then
whenever p A and i ≠ j, and
whenever i ≠ j and i ≠ k. These two equations, together with the other elementary properties of an equality, can be summed up by saying that a polyadic algebra with an equality is a cylindric algebra in the sense of Tarski.
THEOREM 13. If E is an equality for A and if D(i, j) = { p A: S(i/j)p = 1}, then the set D(i, j) has an infimum in A for each i and j, and that infimum is equal to E(i, j)
It is a consequence of Theorem 13.13 that a polyadic algebra can have at most one equality. The theorem does not say that D(i, j) always has an infimum in A (it does not) or that, if it does, then A must have an equality (it need not). The parenthetical negative assertions are established by the construction of explicit counterexamples.
THEOREM 14. Every polyadic algebra is a polyadic subalgebra of an algebra with equality.
It follows from this result that every polyadic algebra can be imbedded into a cylindric algebra. (Here the given algebra may have finite degree, or else it need not even be locally finite ; if, however, it is locally finite, then the imbedding algebra can be made to be locally finite also.) The logical counterpart of Theorem 14.14 asserts the consistency of equality. One way to put it is this: a consistent first-order functional calculus remains consistent when a sign of equality is adjoined to its symbols, and the usual requirements on an equality are adjoined to its axioms,
7. Algebras with Equality.—Suppose that I is a set, X is a non-empty set, and B is a Boolean algebra. If i and j are in I, let E0(i, j) be the function from XI into B such that E0(i, j) (x) = 1 or 0 according as xi = xi or xi ≠ xj. The function-valued function E0 is called the functional equality associated with I, X, and B. The terminology is justified by the fact that whenever all the values of E0 (i.e., all the functions E0(i, j)) belong to a B-valued functional I-algebra with domain X, then E0 is an equality for that algebra.
If E is an equality for a B-valued functional I-algebra A with domain X, it is not necessarily true that E coincides with the associated functional equality E0. It is true, however, at least in the important O-valued case, that a suitable modification converts E into E0. The process (an algebraic modification of known logical methods) involves the introduction of an equivalence relation in X induced by E and the reduction of X modulo that relation. The end-product of the process is conveniently described in terms of a new definition: the equality E will be said to be reduced if (for all i and j in I and for all x in XI) E(i, j) (x) = 1 implies that xi = xj. The result is that A is isomorphic to a B-valued functional I-algebra with a reduced equality. The most useful part of this result is the following special case.
THEOREM 15. Every O-valued functional polyadic algebra with equality is isomorphic to an O-valued functional algebra A0 such that the associated functional equality E0 is an equality for A0.
These results (together with the known representation theorems for polyadic algebras) imply the algebraic version of the completeness theorem for the first-order functional calculus with equality.
8. Unique Existence.—An existential assertion (“there is at least one i such that q”) corresponds in algebraic terms to an element of the form (i)q. The algebraic correspondent of an assertion of uniqueness (“there is at most one i such that q”), to be denoted by !(i)q, is defined (in an algebra with equality E) by
(If J is a subset of I, the operator ∀(J) is defined by ∀(J)p = ((J)p') '.) The auxiliary variable j here is to be distinct from i and such that q is independent of j; the definition is easily shown to be independent of the particular choice of j. The algebraic correspondent of an assertion of unique existence (“there is exactly one i such that q”), to be denoted by !(i)q, is defined by !(i)q = (i)q ∧ !(i)q.
THEOREM 16. If J is a finite set not containing i, if J ∪ {i} supports q, and if !(i)q = 1, then there exists a unique J-term t of A such that S(i/t)q = 1.
The term t constructed in Theorem 16.16 (“the i such that q”) will be denoted by ⊥(i)q. (The traditional symbol is an inverted iota instead of an inverted T.)
The similarity between the theory of predicates and the theory of terms is clearest in the presence of an equality. There is, in fact, a natural one-to-one correspondence between all operations and some predicates. The relevant predicates are the single-valued ones. An (n + 1)-place predicate P is single-valued (with respect to its first n arguments) if !(j)P(i1 . . . , in, j) = 1 whenever (i1 . . . , in) In and j I – {i1 ...,in}.
THEOREM 17. If T is an n-place operation and if
whenever (i1 . . . , in, j) In+1, then P is a single-valued predicate (with respect to its first n arguments). If, conversely, P is an (n + 1)-place predicate that is single-valued with respect to its first n arguments, then there exists a unique n-place operation T satisfying the preceding equation; the operation T is such that
whenever (i1 . . . , in) In and j I – {i1 . . . , in).
1 “Polyadic Boolean Algebras,” these PROCEEDINGS, 40, 296–301, 1954.
2 ‘Algebraic Logic. I. Monadic Boolean Algebras,” to appear in Compositio Math.; ‘Algebraic Logic. II. Homogeneous Locally Finite Polyadic Boolean Algebras of Infinite Degree,” to appear in Fundamenta Math.
3 They will be Parts III and IV of a sequence of papers appearing under the main title “Algebraic Logic.”