Standard Positioning Service (SPS) This service is available freely to the general public for civilian applications. Position is set by using the coarse acquisition (C/A) signal.This chapter deals with the specifications of the dual GPS/Galileo RF front-end. As the starting point for the design of the RF front-end, a study of the technical issues related to the signals of the GPS and Galileo standards is shown. This is employed to obtain the specifications of an interoperable dual GPS/Galileo RF front-end, which is explained in the second part of this chapter.
In this chapter, the GPS and Galileo standards are explained in more detail. Specifications of the RF front-end must be determined in response to the signals transmitted by the satellites.
The development of the Navstar GPS took nearly 20 years and cost more than $10 billion. It is the first and currently the only fully operational Global Navigation Satellite System (GNSS). The GPS project began in 1973 and attained full operational capability (FOC) in 1995, although it was already in use at the beginning of the 1980s. Developed by the U.S. Department of Defense (DoD), GPS is intended to serve as primary means of radio navigation well into the twenty-first century. GPS replaced less-accurate systems such as LORAN-C, OMEGA, VOR, DME, TACAN, and Transmit.
GPS has become much more than a military navigation platform since it has been opened to civilian use. Many new civil applications have appeared over the last few years in response to the decreasing cost, size, and power consumption of GPS receivers. Moreover, receiver capabilities continue to improve and small multichannel receivers with sophisticated tracking, filtering, and diagnostic features are making even advanced applications possible.
The civil uses of GPS include, but are not limited to, marine and aviation navigation, precision timekeeping, surveying fleet management (rental cars, taxis, delivery vehicles), aircraft approach assistance, geographic information systems (GIS), wildlife management, natural resource location, disaster management, meteorological studies, and recreation (hiking and boating)[HP AN1272].
Any GNSS consists of three different parts, namely the space segment, ground segment, and receiver. The space segment is composed of the satellites in space, whereas the ground segment controls the operation of the system from the Earth. Varying degrees of accuracy and services can be obtained depending on the receiver in use.
The GPS space segment is comprised of 24 Navstar satellites (and one or more in-orbit spares) distributed throughout six orbital planes. It takes 12 hours for the satellite to orbit the Earth, during which time it will have travelled 10900 nautical miles (approximately 20200km) orbits, meaning that each satellite passes over the same location on the Earth roughly once a day. Normally, five satellites are within range of users worldwide at any given moment. During the last 28 years, four different generations of GPS satellites have been developed: Block I, Block IIA, Block IIR (replenishment), and Block IIF (follow-on). The average lifespan of the first three generations of satellites is from 7 to 10 years, while the last generation is expected to last 15 years.
First launched in 1997, Block IIR satellites make up the majority of the current constellation of satellites. Block IIR satellites are equipped with an auto-navigation capacity (AUTONAV) that allows each spacecraft to maintain full positioning accuracy for at least 180 days without Control Segment support. The latest satellites in this series (Block IIR-M) carry a new military code or M-code. The M-code will be more jam-resistant than the current military GPS code (also known as P-code). In addition, these satellites will offer a second civil signal on the L2 band. Beyond the Block IIR-M, there are also plans to upgrade the system through the introduction of the GPS IIF programme (its first launch is planned for 2008). The Block IIF programme will transmit a third civil signal on the L5 band. A fifth generation of GPS satellites, Block III, is expected to dramatically enhance the performance of the system. It will add a third signal on the L1 and L2 bands (for which the first launch is planned for 2012). These satellites will provide a more resistant, accurate, and reliable signal through increased transmission power.
The ground segment consists of different stations scattered throughout the world. A master control station in Colorado Springs controls the space segment. In addition to operating the master control station, the United States operates five unmanned monitor stations and four ground antennas to pick up GPS satellite signals. The data collected by the monitor stations are used to calculate positioning corrections for the satellites. This process ensures the synchronisation of the satellites and the accuracy of the signals sent to the Earth.
There are two types of GPS terminals, categorised according to the code they can acquire. The services available depend on the code received. Therefore, depending on the receiver, the offered services are as follows:
Standard Positioning Service (SPS) This service is available freely to the general public for civilian applications. Position is set by using the coarse acquisition (C/A) signal.
Precise Positioning Service (PPS) PPS receivers are used exclusively by authorised government agencies. Military receivers do not have to go through the C/A signal to track the P(Y) signal. Then, once military personnel is equipped with PPS receivers, C/A signal can be switched off on the battlefield without fear of repercussions for friendly military forces[Kaplan96].
A GPS satellite currently sends signals L1 and L2 with a central frequency of 1575.42MHz for L1 and 1227.6MHz for L2, as shown in Figs. 2-1 and 2-2. There is a third signal, defined as L3, sent by satellites with a central frequency of 1382.05MHz. This signal will not be covered in this book due to the fact that it is employed by the Nuclear Detonation Detection System (NUDET) and has no navigation finality.
Figure 2-1 shows how L1 and L2 are built. The L1 signal is a QPSK signal modulated in phase by the C/A-code and the information of the navigation message, and in quadrature by the precision code (P-code) and the navigation message. The L2 signal is a BPSK or QPSK signal modulated by a single signal, the C/A-code, the P-code, or the P-code and the information of the navigation message, depending on the selector position.
Figure 2-2 shows the baseband spectrum of the signals for a normalised transmitted power of 1W while Eq. 2-1 and Eq. 2-2 express the signals analytically.
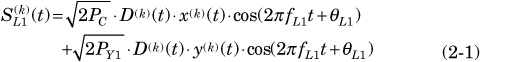
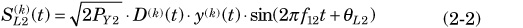
Figure 2-1 Signals sent by a GPS satellite
In Eq. 2-1 and Eq. 2-2, the square root is the signal amplitude (sqrt(2Pc)), D(k)(t) is the navigation message, x(k)(t) and y(k)(t) are the acquisition codes (spread spectrum codes), and fL1 is the carrier frequency.
The coarse acquisition code C/A is also a pseudorandom noise (PRN) code with a clock frequency of 1.023MHz. It is the basis for the code-division multiple access (CDMA), used to send the signal from the satellites to the receivers. Every satellite has a unique C/A-code. These signals are detected and then separated through these codes, which have high-quality cross-correlation properties. This acquisition code constitutes the basis for the service used by the civilian SPS.
The P-code is a 10.23MHz frequency PRN code It is unique for each satellite and used for codification purposes. As PPS bases its service on this code, it is exclusively for military use.
This book focuses on the civilian use of the receiver. Thus, the frequency band considered is the one due to the C/A-code, plus the navigation message, which is 2.046MHz centred on the 1575.42MHz frequency. The signal located on the L2 band will not be considered for the dual
Figure 2-2 (a) L1 signal spectrum; (b) L2 signal spectrum
GPS/Galileo RF front-end dealt with in this book. Commercial receivers only employ the L1 band. Before 1 May 2000, employing the C/A-code on L1 and with the Selective Availability switched on, the 3D accuracy was around 25-100m, 95 percent of the time. Nowadays, employing the C/A-code on L1, and with the SA set to 0 the 3D accuracy, it is around 6-11m 95 percent of the time. New civil signals will offer an improved accuracy, integrity and continuity of service.
The U.S. DoD is planning to renew the GPS satellite constellation. Twenty-nine new satellites are being launched between 2003 and 2012. These satellites will send not only current signals but also additional ones that will allow more accurate and reliable positioning.
Four new signals are expected to be used: two for military purposes on the L1 and L2 bands, and two for civil use on the L2 band and the new L5 band. Since this book is not focused on military applications, only those signals used by civilians are discussed in this section.
Figure 2-3 L2 sent by GPS satellites
The L2 signal sent by new satellites can be expressed analytically as follows:
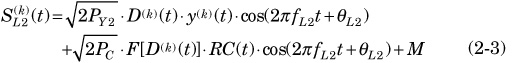
where the first term represents the signal being currently sent as shown in Eq. 2-3. The second term represents the signal for civilian use. The generation of the signal, a 1227.6MHz (fL2) frequency signal modulated by two codes, is shown in Figure 2-3. Navigation messages are coded by Forward Error Correction (FEC) techniques. The last term represents the new signal for military purposes, the details of which are unknown.
The new signal uses C/A-code or another different one from what it is used now, the replacement code (RC), as acquisition code. The C/A is a PRN-code with a clock frequency of 1.023MHz. Compared to C/A, the new RC-code is significantly longer.
By means of this signal and the one on the L1 band, a civilian receiver will be able to correct delays caused by the ionosphere and troposphere, offering more accurate positioning than they do now.
Figure 2-4 shows the spectrum for the new signal of the L2 band. Signal bandwidth is 2.046MHz, the same as the civilian signal of the L1 band.
The L5 signal will be transmitted by the new satellites (from Block IIF) and can be expressed analytically as follows:
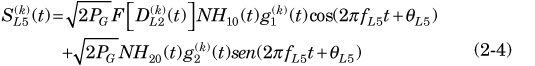
Figure 2-4 Spectral power of the L2 band's new signal
It is a QPSK signal phase modulated by g2(t) and NH20(t) codes and in quadrature by F[DL2(k)(t)], NH10(t), and g1(k)(t) codes. The codes g1(t) and g2(t) are PRN codes with a clock frequency of 10.23MHz. Thus, the bandwidth of the RF-modulated signal is 20.46MHz. NH10(t) and NH20(t) are Neumann-Hoff codes with a clock frequency of 10.23MHz. They increase the size of the g1(k)(t) from 10230chips to 1023000chips and g2(k)(t) from 10230 chips to 204600chips. The carrier frequency (fL5) is 1176.45MHz.
Figure 2-5 shows how to obtain the new L5 signal and Figure 2-6 illustrates the spectrum of the signal.
As in the case of the L2 band signal, the signal on the new L5 band can be used together with the L1 band signal to eliminate the effect of
Figure 2-5 Signal L5 sent by GPS satellites
Figure 2-6 Spectral power of the new signal on the L5 band
the delays caused by the ionosphere and troposphere, thus obtaining more accurate positioning.
Moreover, Block III satellites will add a new civilian signal, called L1C, which will be transmitted on the L1 carrier frequency in addition to the C/A-code signal. The development of L1C represents a new stage for GNSS; the signal is not only designed for GPS transmission, it will also be interoperable with Galileo's Open Service signal centred on the same frequency[Betz06].
Table 2-1 briefly shows the current signals of GPS satellites and the signals of the new generation, planned to be in use starting in 2012.
TABLE 2-1 Signals sent by the new GPS satellite constellation [ARINC00]
Frequency band |
L1 |
L2 |
L5 |
Channels |
A B C |
A B C |
I Q |
Frequency |
1575.42MHz |
1227.6MHz |
1176.45MHz |
Modulation type |
A,B QPSK C → BOC(1,1) |
A,B → BPSK or QPSK C → BOC(10,5) |
QPSK |
Bit rates |
A → 1.023MBs B → 10.23MBs C → 1.023MBs |
A → 1.023MBs B → 10.23MBs C → 5.115MBs |
I,Q → 10.23MBs |
Minimum received power @ elevation 10° |
A → -131dBm B → -128dBm C → -127dBm |
A → -134dBm B -130dBm C → tbd |
I,Q -128dBm |
In the future, civilian users will be offered three kinds of receivers depending on their location accuracy[ARINC00]:
Current receivers will still work with the same accuracy as now tens of metres, and should be sufficient for certain applications.
Dual receivers that receive and process two signals, L1 and L2 or L1 and L5, will be more accurate, metre level. This is achieved by correcting delays caused by the ionosphere and troposphere, offering more accurate positioning.
High-accuracy receivers will make use of signals L1, L2 and, L5. These kinds of receivers will offer centimetre-level accuracy and will be required to be differential.
In 1998, the European Space Agency (ESA) and the European Commission jointly decided to study the feasibility of a truly independent European GNSS. Named Galileo, the program was first approved in 1999. Besides being independent, Galileo is expected to offer greater accuracy, integrity, availability, and continuity of services compared to present systems. In spite of the dual-use nature of any GNSS system, Galileo is intended for civilian application only. It has been deemed a "civil programme under civil control."
Being civilian-friendly means that, so far, none of Galileo's funding has come directly from defence budgets. With deployment costs estimated between €3.2–3.6 billion, funding is expected to come from public-private partnerships (PPP) and fee-for service charges to be collected by the Galileo Operating Company (GOC). Total costs, including 12 years of operational costs, are likely to reach €6 billion. With respect to partnerships, the European Investment Bank and a number of private enterprises are collectively planning to pledge a minimum of €5 million to the project. They may team up with Joint Undertaking (JU), which is presently responsible for the development and validation phase. To avoid conflicts of interest, private enterprises may not become members until the tendering process has finished.
Like any GNSS, Galileo consists of the space segment, the ground segment, and the user receiver. The space segment will be comprised of 30 satellites (27 active and 3 spare) in the Medium Earth Orbit (MEO) at an altitude of 23600km. The satellites will travel along three circular orbits at an inclination of 56°, ensuring global coverage. With a satellite orbit time of 14 hours, the configuration of the constellation will guarantee at least six in-sight satellites at any given time for any location, including the poles.
The Galileo satellites will have an expected lifespan of 10 years. Individual satellites will be replaced on a regular basis to account for eventual malfunctioning, residual life, and accommodation of future payload technology.
The space segment will be managed by two control centres located in Europe, supported by 20 Galileo Sensor Stations (GSS). Data exchanges between the control centres and the satellites will be carried out through specific uplink stations. A total of 15 uplink stations will be installed around the world to facilitate this type of data transfer. As the principal component of the ground segment, the control centres will be responsible for the management of the satellites, the integrity of the signals, and the synchronisation of the atomic clocks onboard the satellites.
Galileo satellites will transmit ten different signals located on the following bands: E5a and E5b (1164–1215MHz), E6 (1260–1300MHz), and E1-L1-E2 (1559–1592MHz). Six signals will be devoted to civilian (Open Service) and Safety of Life (SoL) services, two for commercial users, and the remaining two (Public Regulated Services, or PRS) for official/regulated personnel. Apart from these timing and navigation transmissions, Galileo will provide information concerning the accuracy and status of its signals. Known as "integrity messages," these signals are specifically geared for SoL applications, although they are likely to be offered to service industries requiring legal guarantees (during the transportation of valuable goods, for example). The services offered by Galileo are as follows:
The Open Service (OS) will be available to civilian users free of charge and will accurately provide positioning, speed, and UTC time. According to the plans of the European Commission, the quality of the OS will be better than that of the present and future GPS civil services. It will be offered by the E5a, E5b, and E1-L1-E2 bands.
The Commercial Service (CS) will operate under a fee-for-service plan. As such, access to the CS will require a payment to the GOC through the service provider in return for the encryption keys required to receive the signals. Compared to the OS, CS signals will be of a higher quality and will guarantee a certain level of reliability and accuracy. Service will be provided by signals located on E5b, E6, and E1-L1-E2 bands.
The SoL service will offer the same accuracy as the OS but with a high level of integrity. A greater level of integrity is required for an effective and accurate service for companies working in the field of air and maritime navigation. At some stage, SoL may be encrypted and therefore require a fee for access. The Search and Rescue (SAR) service will be a certified service developed in accordance with international regulations. It will provide real-time transmissions of emergency requests to facilitate the location of distress messages. SoL will be provided by the signals on the E5a, E5b, and E1-L1-E2 bands and will be a restricted service.
The Public Regulated Services (PRS) signal will be for governmental use only and is designed to guarantee continuous signal access in the event of threats or crisis. It will require noncommercial receivers that can store the needed decryption keys and will be provided by signals on the E6 and L1 bands. An access-regulated service such as the SoL will also be required.
The goal of this book is to explain the design process of a receiver that will offer basic services to the user. Thus, signals on the E5a, E5b, and E1-L1-E2 bands that make up the Open Service will be described in detail.
Four different signals are sent on the E5 band with a central frequency of 1191.795MHz; E5a and E5b have two components in quadrature each one. The signal modulation is the alternative BOC, AltBOC(15,10). The signal processing techniques required to process AltBOC modulation are much more challenging than those used for traditional BPSK or even for usual BOC modulation. This stems from the extremely large bandwidth and from the complex interaction of four components of the spreading code. It can be assumed that the four signal components on the E5 band are modulated as a single wideband signal generated following AltBOC(15,10) 8-PSK modulation. This wideband signal is centred on the E5 frequency of 1191.795MHz and has a bandwidth of at least 70MHz. AltBOC modulation offers the advantage that the E5a (I&Q) and E5b (I&Q) bands can be processed independently, like traditional BPSK(10) signals, or together, leading to tremendous performance in terms of tracking noise and multipath functions. Characteristics of all four signals are summarized in Table 2-2.
The E1-L1-E2 band is composed of three channels sent by the same carrier (fL1 =1575.42MHz) and modulated through the "modified hexaphase modulation." In baseband, channels B and C will show a BOC(1,1) modulation, while coded information will be sent through flexible modulation BOC(15,2.5) on channel A.
TABLE 2-2 Characteristics of the components of the E5 signal band
Signal component |
Modulation |
Data |
Centre frequency |
E5aI |
BPSK(10) |
Yes |
1176.45MHz |
E5aQ |
BPSK(10) |
No |
1176.45MHz |
E5bI |
BPSK(10) |
Yes |
1207.14MHz |
E5bQ |
BPSK(10) |
No |
1207.14MHz |
TABLE 2-3 Signals sent by Galileo satellites
Frequency band |
E1-L1-E2 |
E5 |
Channels |
A B C |
I Q |
Frequency |
1575.42MHz |
1164-1214MHz |
Modulation type |
B,C → BOC(1,1) A → flexible BOC(15,2.5) |
AltBOC(15,10) |
Bit rates |
A → max 1.023MBs B,C → 2.046MBs |
I,Q → 10.23MBs |
Minimum received power @ elevation 10° |
A → -125dBm B,C → -128dBm |
I,Q → -128dBm |
Table 2-3 summarises the signals of the Galileo satellites that provide the OS. The service will be operative starting in 2012.
After analysing the signals of the GPS and Galileo navigation systems, it can be seen that there are two frequency bands where both systems simultaneously send the navigation message: GPS L1 with Galileo E1-L1-E2 and GPS L5 with Galileo E5 (see Figure 2-7). A GPS/Galileo multistandard terminal should receive signals from one or both frequency bands and be able to provide the position with one or both systems at the same time.
This book aims to show the design process of a RF front-end that receives the signals of the first frequency band, namely GPS L1 and Galileo E1-L1-E2, so the receiver can relay position data with one or both systems at the same time. As the E1-L1-E2 signal bandwidth (24MHz) is higher than the L1 signal (2.046MHz), the former will establish the bandwidth of the input signal that has to be processed.
Figure 2-7 Signals bands sent by Galileo [Chatre05] and GPS [Stansell06]
Once the signals to be received by the front-end are identified, requirements for the receiver have to be defined. Specifications regarding noise, linearity, and bandwidth must be studied to obtain a reliable and accurate positioning through GPS and/or Galileo.
This section deals with the establishment of the specifications for a dual RF GPS/Galileo RF front-end, which is required for proper design and fabrication. The receiver's noise figure, third-order intermodulation product (IP3), and bandwidth requirements are taken from the GPS and Galileo standards analysed in the previous section. These parameters typically determine sensitivity, the lowest signal power that can be received; linearity, which is related to highest signal power that can be received and the frequency bandwidth of the receiver. All these parameters are related to the positioning accuracy and integration time through the BER as it is shown in the Figure 2-8.
The manner in which these are obtained is explained in detail in this section, along with the receiver architecture and the receiver blocks: receiver chain and phase-locked loop (PLL) specifications.
As with any other RF front-end, the parameters that characterise the receiver are the noise figure, linearity, and frequency bandwidth, which will be explained in the following subsections.
GNSS signals are transmitted by medium power satellites, with approximately 40dBm. When they reach the Earth, they are normally received by low-gain, low-power quasi-omnidirectional antennas with a minimum power of approximately –131dBm. Thus, multiple-access noise can be considered second-order noise rather than thermal or white noise. Moreover, [Parkinson96] explains that the transmission channel adds only Gaussian-distributed white noise.
First of all, the BPSK-modulated GPS L1 signal is considered. The error probability for the demodulation of a BPSK signal sent through a channel that considers Gaussian distributed noise can be calculated by Eq. 2-5.
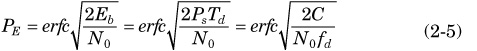
where Eb is the energy per bit, Ps is the power of the received signal, C is the power of the received signal in 1Hz, and fd is 50bps of the navigation message. This provides a valuable parameter to measure the
Figure 2-8 Relationship between various parameters of a GNSS receiver
performance quality of the front-end when it comes to the lowest signal power it can detect: the carrier-power-density-to-noise ratio (C/N0), which is typically given in decibels.
The carrier-to-noise ratio (C/N0) is related to the maximum bit error rate (BER) required for a GPS receiver at the output, which is 10-5 [Parkinson96]. Eq. 2-5 demonstrates that C/N0fd should be above 10 to achieve the necessary BER. If the navigation message has a frequency of 50bps, then the minimum required C/N0 at the output of the RF front-end will be 27dB/Hz. On the other hand, thermal noise density at the input of the antenna is typically –174dBm/Hz and the minimum received input power in the case of GPS is –131dBm[ARINC00]. Therefore, C/N0 at the input of the RF front-end results in 43dB/Hz. Thus, the maximum allowed noise figure can be obtained from the difference between the minimum expected C/N0 at the input and the minimum required C/N0 at the output, which comes out to 16dB.
Let's now move to the BOC (1,1)-modulated E1-L1-E2 Galileo signal. To ensure correct positioning for different receiver designs, the digital part of the receiver must have at least a C/N0 of 30dB/Hz at the output of the RF front-end[Hein02]. Such a C/N0 does not imply an error in the demodulation, it only means a higher or lower accuracy positioning. Figure 2-9 shows how RMS error in metres, due to code tracking error, increases exponentially for values of C/N0 below 30dB/Hz. The thermal noise density at the input of the antenna is typically –174dBm/Hz and the minimum received signal power can be estimated as –128dBm.
Figure 2-9 RMS code tracking error in metres
Therefore, the C/N0 at the input of the RF front-end is 46dB/Hz. Thus, the maximum allowed noise figure (NF) for correct positioning can be set at 16dB. As was calculated for the GPS case, this is the difference between the minimum C/N0 at the input and the minimum required C/N0 at the output.
As the C/N0 values employed for the calculations have been set to meet minimum requirements for a receiver the obtained NF values are the maximum ones allowed. However, not only the NF but also the integration time (T) of the receiver and the signal detection probability determine the quality of the receiver. For a better understanding of the relation among these parameters, an explanation of how a receiver acquires the signal is first required.
The signal acquisition process is a search process where it is necessary to repeat the C/A of the satellite from which the signal is received and the carrier frequency of the modulated code. The received carrier signal presents a frequency variation due to the Doppler Effect as a result of the speed of the satellite in its orbit and the speed of the receiver.
Figure 2-10 shows the bidimensional searching process. The generated C/A-code phase and the generated carrier frequency are swung, obtaining cells that are compared with the received signal by a correlation process. Every cell correlation process lasts T seconds. The decision to maintain or discard the signal is taken by comparing the value obtained in the correlation process with a given threshold value.
Figure 2-10 Bidimensional searching process
Figure 2-11 (a) False alarm probability. (b) False discard probability. Although there is a signal, it is not detected. (c) Signal detection probability. (d) Correct discard probability.
Every comparison has its probability density function (PDF); as there is noise with or without the signal in every cell, the detection process is a statistical one.
Figure 2-11 shows the probability density functions for the reception of the GPS L1 signal, when the decision is taken in the first try. If the obtained value is higher than a threshold value, the signal may be maintained; otherwise, it will be discarded. The signal detection probability Pd, and the false alarm probability Pfa, when maintaining the signal is considered in its absence, can be analytically expressed by Eq. 2-6 and Eq. 2-7.
where ps(z) is the probability density function in the presence of the signal, pn(z) is the probability density function in the absence of the signal, and Vt is a given threshold value.
As phase I and quadrature Q L1 signals are Gaussian distributed, probability density functions ps(z) and pn(z) can be calculated by Eq. 2-8 and Eq. 2-9[Kaplan96].
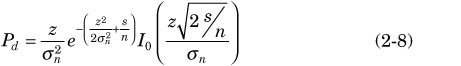
s/n is the signal-to-noise ratio estimated before signal detection (10S/N/10).
S/N is the signal-to-noise ratio estimated before signal detection in decibels and can be calculated by C/N0 +10log T (dB).
T is the integration time for every cell before signal detection.
σn is the root means square (RMS) noise power
For threshold value Vt, defined by Eq. 2-10 and a Pfa of 16 percent, the signal detection probability (Pd) can be calculated from Eq. 2-6 and Eq. 2-8. This results in Table 2-4, which shows Pd depending on C/N0 and T for a normalised unity σn.
The values in Table 2-4 can only be considered a guide as it takes commercial receivers more than one attempt to decide whether to maintain or leave a signal out. The values of the table have been shown here for a better understanding of the relation among the noise figure, signal detection probability, and integration time. Consequently, a proper noise figure can be obtained according to the features of the receiver.
As shown in Table 2-4, the higher C/N0 is, the higher the signal detection probability will be, if it exists. This would, in turn, result in shorter integration time, which results in better receiver performance. This is why this process will require a lower noise figure than the previously defined maximum of 16dB, although it could sufficiently provide for accurate GPS or Galileo positioning.
TABLE 2-4 Detection probability versus C/N0 and integration time T
C/N0 (dB/Hz) |
||||
Pd |
T = 0.001 s |
T = 0.0025 s |
T = 0.005 s |
T = 0.010 s |
0.43105 |
30.00 |
26.02 |
23.01 |
20.00 |
0.63852 |
33.01 |
29.03 |
26.02 |
23.01 |
0.78084 |
34.77 |
30.79 |
27.78 |
24.77 |
0.87185 |
36.02 |
32.04 |
29.03 |
26.02 |
0.92721 |
36.99 |
33.01 |
30.00 |
26.99 |
0.95964 |
37.78 |
33.80 |
30.79 |
27.78 |
0.97807 |
38.45 |
34.47 |
31.46 |
28.45 |
0.98829 |
39.03 |
35.05 |
32.04 |
29.03 |
0.99384 |
39.54 |
35.56 |
32.55 |
29.54 |
Another reason for requiring a lower noise figure lies in the increasing use of GNSS receivers in urban environments. The received signal power is reduced in places with high buildings and narrow streets, reaching values of C/N0 around 15dB/Hz in some cases. In this case, the receiver is unable to detect the satellite signal or provides an imprecise position. Moreover, another factor to consider in urban environments is the presence of interference signals that the receiver can capture, increasing SNR degradation.
A maximum noise figure of 3.5~4dB has been defined taking all these reasons into account. These values have been taken from an exhaustive study of commercial GPS receivers, making the receiver compatible with any detection method used today.
Receiver linearity requirements for GPS and Galileo receivers are not critical when it comes to the received signal because the power received is very low and practically constant. Linearity requirements are therefore imposed by receiver behaviour to external interferences. Section 2.2.2.3 shows a wider study of this behaviour.
As mentioned in section 2.1.3, the bandwidth of the Galileo signal is higher than that of the GPS signal. To be able to receive all the information sent, designers should choose the highest bandwidth. Nevertheless, lower bandwidth filters lower than those set by the standard can be applied without major damage to the C/N0. Figure 2-12 shows the
Figure 2-12 C/N0 degradation versus receiver bandwidth
Figure 2-13 Power spectral density of a BOC (1,1) and BPSK-modulated signals
correlation loss due to the bandwidth of the filter used for signal reception. It can be seen that for a filter with a bandwidth higher than 14MHz, the degradation of C/N0is less than 0.25dB and losses increase exponentially for a filter with a bandwidth lower than 6MHz. Therefore, a 6MHz bandwidth is specified for the RF front-end to avoid degradation higher than 0.5dB and to be able to filter interferences in neighbour bands. It improves the C/N0 ratio and sensitivity due to lower noise bandwidth.
Figure 2-13 shows that the specified bandwidth comprises the two main lobes of the Galileo BOC (1,1) signal as well as the main lobe of the GPS C/A-code with its two side lobes.
Once the requirements of the receiver have been obtained, a number of important steps have to be carried out prior to starting with the receiver design. First of all, the gain, the C/N0, and the linearity of the front-end have to be set to ensure proper performance of the receiver. Moreover, the receiver architecture has to be chosen and all the blocks and external components have to be specified to meet requirements.
The required gain of the RF front-end is defined by the power at the input of the receiver chain and by the input analogue-to-digital converter characteristics. The received input signal at the antenna has to be amplified until the ADC is able to digitalise it. Thus, the gain can be defined as the quotient of the input and output signal as expressed in the following equation.
where σN(output) is twice the maximum offset of the analogue-to-digital converter estimated to be 50mV [Baghai97] and σN(input) is the RMS value of the noise over 50Ω, which corresponds to –106dBm or 1.12µV (i.e., the threshold noise power at 290K in 6MHz). The system's voltage gain can now be obtained.
Transforming the gain to decibels, it results in:
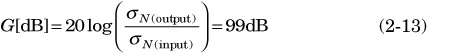
The fact that the specified gain of 99dB is the minimum required gain for the detection of a signal of –130dBm must be kept in mind. If the gain were higher, lower power signals could be detected, thereby improving the sensitivity of the receiver. Moreover, there would be a surplus of the specified gain if the offset of the ADC were higher than the estimated 50mV. On the other hand, if the ADC had a lower offset, the system gain specification could also be decreased. However, this is usually not a contrasted value for the state-of-the-art technology when the time comes for system analysis.
Once it is defined, system gain should be shared among the blocks that compose the receiver. Before doing so, two critical points that determine final features of the receiver have to be taken into account. First, low-frequency amplifiers are more efficient than high-frequency amplifiers in terms of power consumption. Second, material in which the receiver is fabricated has to be able to isolate output and input in order to avoid oscillation problems caused by positive feedback. As an example, a substrate such as the SiGe process of AMS typically presents isolate levels at 1.6GHz below 40dB, while it is close to 90dB at the 3MHz isolation level. Therefore, splitting gain into different frequencies is required.
Eq. 2-14 defines the C/N0 without jamming in the baseband. This parameter is directly related to the behaviour of the receiver under the probability of detecting the signal [Kaplan96].
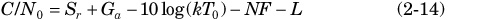
where Sr is the signal power at the input of the system in dBW, Ga is the antenna gain to the satellite in dBic, 10log(kT0) accounts for the thermal noise density in dBW/Hz, NF is the noise figure of the receiver, in dB and L considers the losses in implementation plus the ADC loss in dB. The degradation introduced by the digitalisation of a 1bit ADC can be obtained from [Chang82] and results in 2.2dB.
From the C/N0 required for the system, the noise figure can be calculated by means of the Friis formula or system simulations for a given input signal power, antenna gain, receiver bandwidth, and 1bit ADC from Eq. 2-14. With this relationship, every component of the system can be characterised to make the whole system meet noise specifications.
Noise is usually defined as the floor of the lowest signal power that can be detected. On the other hand, linearity is defined as the ceiling of the highest signal power the system admits before saturation. The span between these two parameters defines the dynamic range of the receiver. Nevertheless, linearity definition should be slightly redefined in the case of GNSS signals because signal power is never high enough to saturate the system.
Even if the received signal is a low-power narrowband signal in the L1 band, signals from close bands, or even intermodulation products of other signals from other bands, could create a signal in the same band as the target signal. This is why linearity in the first blocks of the system is very important. Those signals will affect the performance of the signal processing, as they will not be filtered in the RF front-end. Therefore, the linearity of the GPS/Galileo receiver is redefined as the limit of the highest interference power that the receiver can handle before it begins to perform incorrectly.
As interferences are unwanted signals, they could be considered noise and therefore reduce the value of C/N0 without distortion. In that case, the equivalent carrier-to-noise power density ratio (C/N0eq) can be defined as in Eq. 2-15, where C/N0 and J/S (the jammer-to-signal power ratio) are related to each other.
c/n0 is the carrier power-to-noise without jamming for a 1Hz band expressed as a ratio.
j/s is the jammer-to-signal power ratio expressed as a ratio.
Rc is the chipping rate of the GPS PRN code (chips/sec).
Q is the spread spectrum processing gain adjustment factor (dimensionless).
To obtain the maximum allowed J/S for the receiver, the designer must set the minimum C/N0 for an acceptable receiver (C/N0min) and the specified C/N0 for the receiver to be designed (C/N0) which should be equal or lower than the previous one.
The difference between these two values will be the interference margin (Mint erf), which is the allowed degradation in the C/N0 due to interferences and can be calculated by Eq. 2-16.
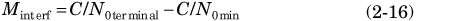
Nevertheless, interferences will not only degrade the C/N0 but also quantification. Thus, even if it has a high enough C/N0, the receiver may not work properly due to erroneous digitalisation. Therefore, depending on the quality of the ADC, the blocking level should be higher than the specified value in Eq. 2-16.
In the case of a 1bit ADC, due to the absence of a gain-controlled amplifier (GCA), interferences could cause the signal to cross the zero level in the input of the converter. In this case, the crossing would be generated by the unwanted interference rather than by a combination of random noise and the navigation signal. This would result in both erroneous digitalisation and incorrect localisation.
The maximum allowed degradation for the SNR in the 1bit quantifier by interference is 14dB Mint erf (Eq. 2-16). This degradation is obtained when J/S is 32dB, which is achieved by an input power signal of –115dBm at the L1 and E1-L1-E2 band frequencies.
A multitude of well-known main RF front-end architectures are in existence: heterodyne, direct conversion, intermediate frequency digitalisation, and direct digitalization. For the combined GPS/Galileo front-end, a low-IF architecture can be selected. This architecture, when compared to Zero-IF, is insensitive to DC-offsets and flicker noise. The DC-offset compensation is a severe problem for Zero-IF receivers, as most of the GPS C/A-code signal energy comes from DC. The main drawback of the low-IF architecture is its limited image rejection. This issue can be minimised when the frequency plan of the entire receiver is carefully designed. If the combined GPS/Galileo L1 signal is down-converted to a low IF of 20.42MHz, if the combined GPS/Galileo L1 signal is down-converted to a low IF of 20.42MHz, the rejection of the image signal by the RF SAW filter can be ensured. The obtained image rejection ratio can reach more than 40dB. By sampling the IF signal at 16.638MHz, the A/D converter also down-converts the incoming signal to a second IF of 4.092MHz. Signal detection is then performed digitally on a second chip that contains all the digital processing and controlling parts of the receiver. The PLL also allows the choosing of a LO frequency that down-converts the incoming RF signal directly to an IF of 4.092MHz. When this is chosen, the image that lies in the GPS/Galileo L1 band mainly consists of thermal noise. Choosing the gain level within the various blocks of the receiver is always a trade-off. A high-gain LNA will help reduce NF by minimising mixer contribution, but at the expense of higher power consumption in this block. A low-gain LNA may improve linearity and power consumption, but would require a low-noise mixer. Such a mixer would consume a lot of power. In other words, a low-gain LNA combined with a low-noise mixer may not offer a significant advantage in total power consumption over a high-gain LNA combined with a mixer with a higher NF. Therefore, a relatively high-gain receiver configuration has been chosen. Moreover, IF digitalisation requires few external components and is relatively simple. Thus, the front-end will consist of passive or active antenna, external filters, the LNA, the mixer, the PLL, amplifiers (RF and IF), and the ADC (see Figure 2-14).
Numerous applications can use a GPS/Galileo receiver. To add felxibility to the receiver, three different structures, both with and without an active antenna and the internal LNA have been studied. Figure 2-15 shows all three structures. Structure (A) makes use of an active antenna, avoiding the use of the LNA of the front-end. As the consumption of the LNA is not required, a very low-power front-end can be employed with a separated voltage supply for the LNA. The (B) and (C) structures employ the LNA and its antenna selection sensor, which sets the working mode of the LNA depending on the use of an active or passive antenna. The (B) structure makes use of an active antenna, which means the LNA is set to work in the low-gain mode so as not to saturate the system. Furthermore, higher sensitivity can be achieved by means of the gain of the external antenna. In the (C) structure, a passive antenna is employed and the LNA is set to the high-gain mode, avoiding the power consumption of the antenna and resulting in a low power consumption system.
Figure 2-14 Block diagram of the receiver
Figure 2-15 Receiver block diagram: (A) with active antenna and without the LNA; (B) with active antenna and the LNA; (C) with passive antenna and the LNA
The specifications of the components of the proposed front-end are shown in Table 2-5. They have been obtained from the exhaustive system analysis of components and system simulations previously explained in this chapter. The supply voltage for the receiver has been defined as 3.3V, the operating temperature range as −30°~ +70°C, and the storage temperature as −40°~ +85°C.
From system simulations and analyses, gain, noise, linearity, and power consumption have been set to every component of the chain to meet required global specifications. Moreover, input and output impedances have been carefully selected to optimise the system gain and minimise the total noise. Due to the high gain required for the IF amplifier, two stages have been defined. If any change is required during the design stage, system simulations can be redone to reset the specifications for the blocks.
Front-end linearity is not an issue, since the received Galileo and GPS signals are low power and relatively constant. Therefore, the linearity specification is dictated by the required system's resistance to external interfering signals. The effects of the interferences on the three different structures previously mentioned have been studied for these specifications (see Table 2-5). They have been obtained from system simulations with a two-tone input. In these simulations, the minimum power that generates a third-order intermodulation product at the studied band
Table 2-5 Receiver chain specifications
Symbol |
Parameter |
Value |
Unit |
LNA |
|||
Gmax |
High mode power gain |
20 |
dB |
Gmin |
Low mode power gain |
8 |
dB |
NFmin |
Noise Figure for Gmax |
2.5 |
dB |
NFmax |
Noise Figure for Gmin |
10 |
dB |
OIP3 |
Output IP3 |
8 |
dBm |
VSWRin |
Voltage stat. wave ratio |
<2 |
---- |
Power |
Current consumption |
7 |
mA |
RF amp. | |||
Gp |
Power gain |
17 |
dB |
NF |
Noise figure |
5 |
dB |
OIP3 |
Output IP3 |
5 |
dBm |
VSWRin |
Voltage stat. wave ratio |
<2 |
---- |
Power |
Current consumption |
6 |
mA |
Mixer | |||
G |
Voltage gain |
6 |
dB |
NF |
Noise figure |
17 |
dB |
IIP3 |
Input IP3 |
−4 |
dBm |
Zout |
Output impedance |
~1400 |
Ω |
Power |
Current consumption |
7 |
mA |
IF_1 amp. | |||
G |
Voltage gain |
20 |
dB |
IIP3 |
Input IP3 |
−15 |
dBm |
Zin |
Input impedance |
~1400 |
Ω |
Zout |
Output impedance |
~2400 |
Ω |
Power |
Current consumption |
3 |
mA |
IF_2 amp. | |||
G |
Voltage gain |
<42 |
dB |
OIP3 |
Output IP3 |
18 |
dBm |
Zin |
Input impedance |
~1400 |
Ω |
Zout |
Output impedance |
~2400 |
Ω |
Power |
Current consumption |
3 |
mA |
Comparator | |||
Voffset—input |
Input offset voltage |
50 |
mV |
Fc |
Clock frequency |
16.368 |
MHz |
Power |
Current consumption |
<1 |
mA |
Figure 2-16 Interference blocking for the three receiver architectures under study
frequency of –115dBm has been obtained. Figure 2-16 shows maximum allowed power at the antenna input for interferences in the vicinity. This interference power corresponds with a J/S of 32dB at the L1 and E1-L1-E2 band frequencies. Then the maximum allowed degradation for the SNR in the 1bit quantifier by the interference can be obtained from Eq. 2-15 and Eq. 2-16 giving a Mint erf of 14dB.
To quantify the interference blocking performance of the receiver an example is considered where the point at which the second harmonic of the result of mixing the signals of Inmarsat at 1645MHz and Iridium at 1610MHz reaches 1575MHz. Moreover, GPS antenna patterns experience attenuation when the elevation angle drops below 5°. The attenuation for the horizon line is typically around 15~20dB[Parkinson96]. Therefore, for a transmission power of 37dBm, the GPS/Galileo receiver can be located 50m from emissions without degrading receiver performance.
A frequency synthesiser, also known as a phase-locked loop (PLL), is a circuit that synchronises an output signal (generated by an oscillator) with an input reference signal to provide a stable and accurate signal frequency. This synchronisation is done in frequency as well as in phase. When both signals are synchronised, phase error is minimised. As in a control system, the output signal phase remains locked with the reference input signal phase.
Any oscillator signal shows instability in frequency and in amplitude. The target of an oscillator is to generate a signal with a fixed frequency. Frequency instability can be characterised through measurements of either frequency or time. In the time domain, the parameter used to measure instability is jitter noise, while phase noise is used to measure frequency. Moreover, frequency error should be below a certain level of parts per million (ppm). The main parameters used to gauge the performance of the synthesiser are phase noise, lateral band (spurious tones), and lock time. However, lock time is not a critical parameter for GPS/Galileo application due to the absence of different channels.
From the analysis of GPS front-ends, it has been observed that several models have digital outputs of 4.092MHz 1bit signals (i.e., [Atmel ATR0603], [Freescale MRFIC1505], [PHILIPS UAA1570HL], [SONY CXA1951AQ], and [ST STB5610]). This frequency is also suitable for the 6MHz bandwidth of the GPS/Galileo receiver. Therefore, a LO frequency of 1571.328MHz is required, which is mixed to the input frequency of 1575.42MHz. Crystal manufacturers offer a quartz crystal for GPS at a frequency of 16.368MHz. Moreover, this frequency is also employed as a clock for the GPS processor. On the other hand, to improve the frequency planning of the receiver, the down-conversion at the mixer is defined for an IF frequency of 20.42MHz. Therefore, a second LO frequency of 1554.96MHz is required. A 4.092MHz digital output is obtained by the ADC at a sampling frequency of 16.368MHz in the ADC. At the 20.42MHz IF frequency, the image signal is attenuated by the RF SAW filter and a higher rejection to the image signal is achieved. Moreover, mixer noise is also lower because it is filtered by the SAW filter. However, a bandpass filter at 20MHz has to be designed. At 4.092MHz, a low pass filter is sufficient, and efficiency of the IF amplifiers can be improved. Unfortunately, the noise and image signal are not filtered through the SAW filters. The frequencies involved in the PLL are summarized in Table 2-6.
A synthesiser based on integer-N architecture (see Figure 2-17) can be used to obtain the required output frequencies. The integer-N PLL has an output signal frequency N times the reference frequency, N being an integer. The output frequency can be changed by varying the value of N.
Table 2-6 Frequencies of the PLL
Fref |
16.368MHz |
Fout1 |
1554.96MHz |
Fout2 |
1571.328MHz |
ADCout |
4.092MHz |
IF1 |
20.42MHz |
IF2 |
4.092MHz |
Figure 2-17 Integer-N PLL block diagram
N is 95 in the case of 1571.328MHz and 96 in the case of 1554.96MHz for the reference frequency of 16.368MHz.
The operation of the PLL is as follows: The output signal frequency is divided to compare it to the reference frequency in the phase frequency detector (PFD). Then the result is applied to a loop filter to obtain a control voltage for the VCO to lock the loop that is achieved when the output frequency is the desired one.
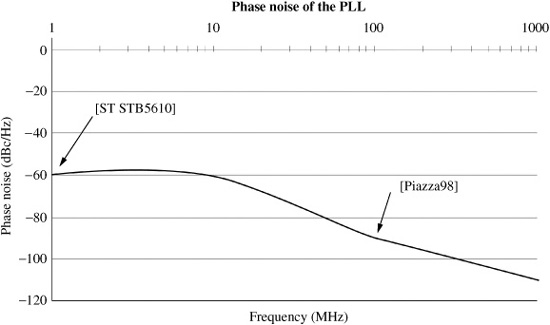
The operation conditions for the PLL have been defined by the system analysis. First, phase noise at the PLL has been defined. Three different zones can be distinguished regarding noise source. For frequencies close to the carrier, noise is generated by the crystal; approximately a decade away from the carrier, noise is contributed by PFD. The VCO is the main contributor to the total noise from a distance equal to the bandwidth of the PLL from the carrier frequency[Quemada07], [Simusyn].
The mask for the phase noise, taken from the analysis, is defined in Figure 2-18. Phase noise of [ST STB5610] has been taken at 1kHz from the carrier and phase noise of [Piazza98] at 100kHz.
The gain of the VCO (KVCO) is defined as the ratio between frequency and voltage variation. From the two working frequencies, 1554.960MHz and 1571.328MHz, a frequency range of ±0.5 percent is obtained. Component tolerance has to be taken into account as well. Inductor value depends only on geometric values, which is why measured integrated inductor tolerance is around ±1.5 percent[Aguilera03]. Thus, a characterisation of the inductors has to be done prior to the design. Capacitor tolerance is typically ±15 percent due to process variation and ±0.24 percent due to thermal variation[AMS]. Considering the resonance frequency shown in Eq. 2-17, the influence of the capacitor and inductor values on the frequency will be ±7.6 percent and ±0.75 percent, respectively.
Finally, a 1 percent safety margin has been defined to set a PLL specification for the output frequency range of around 10 percent (Eq. 2-18). Therefore, adding tolerance to the working frequencies, the VCO output signal has to oscillate between 1408MHz and 1717MHz.
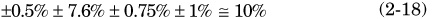
Once frequency variation is obtained and control voltage is set between 0.5V and 2.8V, VCO gain equals 135MHz/V (Eq. 2-19).
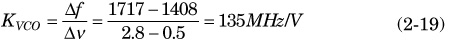
Basic specifications for the PLL are summarised in Table 2-7.
The Agilent ADS templates provide an environment to model PLL performance. Open and Closed Loop Simulation of PLL and PLL_Noise Contribution templates are used to characterise the PLL and analyse its noise, respectively.
2ndHarm |
Spurious response, 2nd harmonic |
<−23 |
dBc |
PN |
Phase noise@ 100kHz |
<−90 |
dBc/Hz |
Pout |
Output power |
0~3 |
dBm |
Vcontrol |
Control voltage |
0.5−2.8 |
V |
Current |
Current consumption |
<−9 |
mA |
TABLE 2-8 Input values for the Open and Closed Loop Simulation of PLL template of ADS
Fref |
16.368MHz |
Fout1 |
1554.96MHz |
Fout2 |
1571.328MHz |
KVCO |
135MHz/V |
Kd |
100µA |
ωp |
40kHz |
With the Open and Closed Loop Simulation of PLL template, a frequency response simulation can be carried out. Nevertheless, lineal models for the VCO, the divider, and the PFD are employed and no phase noise characteristics are considered. The input values for the simulation are shown in Table 2-8. KVCO has already been defined in the previous section. Kd is the current of the charge pump and has been taken from the analysis and PLL simulations that set out to minimise it. Finally, the bandwidth, which is set by the loop filter, is chosen according to the highest value that fulfils the noise and PLL specifications. The absence of different channels in the application offers freedom to choose the loop bandwidth value. The higher it is, the more time it requires to lock the loop and the lower the noise at the output. The bandwidth is set by the loop filter and has an influence on the output noise[Quemada07].
The band attenuation and loop filter components that meet the requirements are obtained from the simulations. The phase margin should be between 30° and 70° as stated in[Wolaver 91]. For a phase margin around 50°, an attenuation of 29/30dB and a bandwidth of 40kHz are obtained. The values of the third-order loop filter (see Figure 2-19) have been obtained from these results and are shown in Table 2-9.
Figure 2-20 shows the VCO phase noise contributors and phase noise mask obtained by the PLL_Noise Contribution template for the previously set values. As explained, for frequencies close to the carrier,
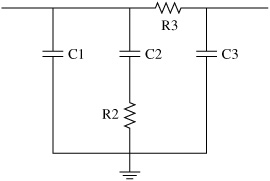
Figure 2-19 Loop filter circuit scheme
Component |
Value |
Unit |
C1 |
659 |
pF |
C2 |
3.27 |
nF |
C3 |
65 |
pF |
R2 |
3.141 |
kΩ |
R3 |
813 |
Ω |
noise is generated by the crystal. Approximately a decade from the carrier, noise is contributed by PFD from a distance equal to the bandwidth of the PLL from the carrier frequency; the VCO is the main contributor to the total noise[Quemada07]. It can be seen that phase noise requirements can be fulfilled, accomplishing the previously defined set of design specifications.
The front-end has been specified in order to work simultaneously with GPS and Galileo. This has been made possible by a study of the two standards, and the analysis of their requirements and system simulations. Therefore, the next objective, the design of the front-end, can be undertaken.
Figure 2-20 PLL_Noise Contribution template results for the PLL phase noise
