5
Wittgenstein and Russell

GRAHAM STEVENS

1 Introduction

Bertrand Russell’s influence on Wittgenstein, personally and philosophically, was profound. Russell’s work on the foundations of mathematics apparently played a decisive role in persuading Wittgenstein to abandon his aeronautical engineering studies in favor of philosophy. In 1909, while still studying engineering at Manchester, Wittgenstein wrote to Philip Jourdain, suggesting a solution to Russell’s paradox. Jourdain, with Russell’s approval, dismissed the solution (Monk, 1990, p.33; cf. LUDWIG WITTGENSTEIN: A SKETCH OF HIS LIFE). But Wittgenstein appears to have been hooked by the subject Russell’s writings had introduced him to and, two years later, he arrived in Cambridge and commenced his philosophical studies with Russell. Russell perhaps did not realize the tremendous personal significance of his positive appraisal of Wittgenstein’s intellectual promise. According to Monk:

Wittgenstein later told David Pinsent that Russell’s encouragement had proved his salvation, and had ended nine years of loneliness and suffering, during which he had continually thought of suicide […]. The implication is that, in encouraging him to pursue philosophy and in justifying his inclination to abandon engineering, Russell had, quite literally, saved Wittgenstein’s life.

(Monk, 1990, p.41)

Wittgenstein’s influence on Russell turned out to be profound as well: two years after they first met, Wittgenstein had delivered an objection to Russell’s theory of judgment that was so devastating that it led to the abandonment of a major philosophical project of Russell’s, leaving him reportedly “paralysed” (Wittgenstein, letter to Russell, 22 July 1913). Wittgenstein’s own work during this period culminated in his Tractatus Logico‐Philosophicus, a book which was published largely thanks to Russell’s support, and which is so deeply indebted to Russellian themes (either as sources of agreement or disagreement) as to be incomprehensible to anyone unfamiliar with Russell’s work.

Wittgenstein’s later philosophical work was far less influential on Russell. We can get a clear measure of Russell’s relative evaluations of the “early” and “later” Wittgenstein from what he has to say in My Philosophical Development (1959), an intellectual autobiography to which an entire chapter was devoted to discussing Wittgenstein’s influence on him (cf. also Chapter 1, WITTGENSTEIN’S PHILOSOPHICAL DEVELOPMENT). “Wittgenstein’s doctrines influenced me profoundly,” Russell writes, explaining that the impact of Wittgenstein came in “two waves” – one shortly before World War I, and one shortly after. However: “His later doctrines, as they appear in his Philosophical Investigations, have not influenced me at all” (Russell, 1959, p.83). Wittgenstein held much of Russell’s later philosophy in similar disdain. No doubt personal issues between the two men, whose once close friendship deteriorated in later years, go some way toward explaining their attitudes toward each other. Certainly it explains the petty, sniping, quality of some of the comments each made regarding the other. Here is Russell on Wittgenstein:

I have not found in Wittgenstein’s Philosophical Investigations anything that seemed to me interesting and I do not understand why a whole school finds important wisdom in its pages […]. [T]he later Wittgenstein […] seems to have grown tired of serious thinking and to have invented a doctrine which would make such an activity unnecessary.

(Russell, 1959, p.161)

And Wittgenstein on Russell:

Russell’s books should be bound in two colours […] those dealing with mathematical logic in red – and all students of philosophy should read them; those dealing with ethics and politics in blue – and no one should be allowed to read them.

(Letter to Drury, cited RW 112)

But there is a genuine philosophical point of division that explains this mutual hostility, revealed perhaps most explicitly by Wittgenstein’s comment that “‘Mathematical logic’ has completely deformed the thinking of mathematicians and philosophers” (RFM V §48). What this comment reveals is that the later Wittgenstein rejects the entire methodology of Russell’s philosophy. The rejection is so fundamental as to leave no real room for philosophical interaction between the two. In what follows, I will be exclusively interested in the early interaction between Wittgenstein and Russell. In particular, I will seek to uncover just what it was that Wittgenstein objected to in Russell’s philosophy of 1913 and why this objection had the devastating impact on Russell that it did.

2 Russellian Background

To fully appreciate the underlying concerns of the Tractatus it is important to understand the extent to which Wittgenstein is responding to themes in Russell’s philosophical logic. Two fundamental elements are pivotal to the logicism of Russell’s Principles of Mathematics (1903): his conception of a proposition, and his commitment to the doctrine of the unrestricted variable.

When Russell first advanced the logicist thesis that mathematical truth is a species of logical truth in his Principles of Mathematics, he adhered to a very simple and elegant ontology. At this time, Russell insisted that there was only one fundamental ontological category, the category of what he called terms. Russellian terms, it should be noted, are not (generally) linguistic items but the meanings of linguistic items:

Whatever may be an object of thought, or may occur in any true or false proposition, or can be counted as one, I call a term. This, then, is the widest word in the philosophical vocabulary […] and to deny that such and such a thing is a term must always be false.

(Russell, 1903, sec.47)

Russellian propositions are also nonlinguistic. They are the meanings of declarative sentences, and are composed of the terms that are the meanings of the words of those sentences.

In Russell’s technical development of the logicist thesis, this ontological principle finds its formal counterpart in what has come to be called “the doctrine of the unrestricted variable.” This doctrine maintains that any term may be the value of a variable of pure logic. Having adopted the doctrine that whatever can be an object of thought must be a term, Russell maintained that it is self‐contradictory to deny that a term could fail to be a suitable logical subject for any proposition (see 1903, sec.52). But to deny the doctrine of the unrestricted variable is, in effect, to deny this. For if we maintain that only entities of a certain restricted sort may be values of the variable “x” in a monadic propositional function “φx,” we are effectively committing ourselves to denying that every entity is a value of the variable in the propositional function “x is a term”; but as we saw above, Russell thinks that such a denial must “always be false” (sec.47). The doctrine of the unrestricted variable, then, is a key commitment of Russell’s metaphysics in 1903.

Let us now examine Russell’s notion of a proposition. Russellian propositions, as we now call them, are abstract entities that contain the objects that they are about (rather than, e.g., modes of presentation of those things, as Frege proposed). So, for example, the proposition that Socrates is mortal is a complex composed of the individual Socrates and the property of mortality. There are numerous reasons why this notion of a proposition was appealing to Russell, many of which anticipated important contemporary work on direct reference semantics. However, it also raised some seemingly intractable difficulties regarding belief reports, informative identity statements, and the semantics of empty names. Russell (mistakenly) thought that a combination of his famous theory of descriptions, along with his infamous theory that names are disguised definite descriptions, would resolve such difficulties.

But a further problem remains: what is the difference between a true proposition and a false proposition? Russell identified true propositions with facts. But false propositions are just as real as true ones. So Russell’s ontology now must be extended to include fact‐like falsehoods. These non‐facts differ from facts only by virtue of lacking the property of truth. Why they lack this property while truths have it, Russell claimed, is “incapable of analysis”; it is simply the case that “some propositions are true and some false, just as some roses are red and some white” (Russell, 1901, pp.75–6).

In addition to these ontological problems facing his theory of propositions, Russell also became convinced that his ontology of propositions contained fundamental logical problems, as he encountered recurring contradictions in his attempts to formalize a propositional logic that would comport with his philosophical theory. Under such pressures, he abandoned his ontology of propositions shortly prior to the completion of the first volume of Principia Mathematica in 1910. In place of his theory of propositions, Russell now developed a new theory of propositional content that has come to be called the Multiple‐Relation Theory of Judgment (MRTJ). When committed to propositions as the objects of propositional attitudes, Russell naturally construed judgment as a dyadic relation between an agent and a proposition. On the MRTJ, this is replaced by a radical new analysis.

3 The Multiple‐Relation Theory of Judgment

On the MRTJ, truth ceases to be a matter of identity between propositions and facts, evolving instead into a relation of correspondence between judgments and their truthmakers. Judgment is now analyzed as a many‐placed relation (n‐placed where the number of constituents of the judgment’s truthmaker is n – 1). So, for example, a subject s’s judgment that aRb will be analyzed as:

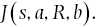
Russell was no doubt struck by the many advantages of this new analysis of belief. Perhaps most importantly, the MRTJ has a role to play in the justification of the order‐part of the ramified hierarchy of types in Principia by shifting at least that part of the hierarchy onto Russell’s epistemology rather than his ontology. Previous incarnations of that theory applied the hierarchy to propositions, thus resulting in an infinite number of different orders of proposition, a position that Russell struggled to make sense of as a metaphysical doctrine. But with propositions rejected, Russell thought that the imposition of this hierarchy onto judgments was less problematic, for the simple reason that judgments were not mind‐independent elements of his ontology. Hence, Russell thought, the logical doctrine of orders (explained later in this chapter) did not have to extend into his metaphysics. Furthermore, as many have noted, the shift to a correspondence theory of truth relieved Russell of some outstanding ontological debts incurred by his earlier identity theory of truth, such as the problem of explaining what the ontological status of false propositions was.

The theory was not without problems of its own, however. In fact these problems are not really new problems, they are new forms of an old problem: the problem of the unity of the proposition. Central to the project of analysis endorsed by Russell and Moore at the turn of the nineteenth to the twentieth century was the idea that propositions are to be analyzed by breaking them down into their constituent parts. But this conception of analysis immediately invites the problem of the unity of the proposition, for there is a clear difference between the proposition that Socrates is mortal and the collection {Socrates, mortality}. No amount of listing or aggregation of the constituents of a proposition is going to be the same as that proposition which has a unity lacking from lists or aggregates. The problem of the unity of the proposition is just the problem of explaining what this difference consists in.

This problem, explicitly recognized by Plato and occasionally surfacing without solution in discussions of propositional content ever since, is notoriously hard to solve. For whenever a candidate is suggested as guarantor of propositional unity, the question arises whether this candidate is itself a constituent of the proposition. If it is not, then it can hardly provide the unity; if it is, we face the question of what relates this new entity to the other constituents so as to make them all cohere into a unity. If the answer to that question is “nothing,” then the new constituent can hardly provide the unity, if the answer is that another relation does the relating, we can ask the same question of this new relation and, obviously, find ourselves propelled onto an infinite regress.

The problem re‐emerges in the context of the MRTJ in two new forms, often referred to as the “Direction Problems.”

4 The Narrow Direction Problem (ND)

Consider Othello’s belief that Desdemona loves Cassio:

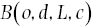
B is a many‐placed relation over o,d,L,c. But in that case what is the difference between Othello’s belief that Desdemona loves Cassio and his belief that Cassio loves Desdemona? At first Russell thought the order needed to distinguish the two beliefs could be provided by the subordinate relation (L), but this won’t do as L has to be one of the objects related by B – it cannot be what Russell calls a “relating relation”: “The relation ‘loving,’ as it occurs in the act of believing, is one of the objects – it is a brick in the structure, not the cement” (Russell, 1912, p.74). In The Problems of Philosophy (1912) Russell instead suggested that the order is provided by the primary relation (B). But, as he soon came to see, simply bestowing that property on B leaves the property wholly mysterious. To say that belief – i.e., believing –somehow orders its objects is not an explanation of the ordering of beliefs, of what is believed: it is a labeling of a problem, not a solution. Eventually Russell (1913/84) settled on invoking “logical forms” to provide the order where necessary. Logical forms act as templates in which elements are assigned a position. Thus, in addition to Othello, Desdemona, love, and Cassio, the belief‐complex under discussion will also include (or at least somehow involve; see below) a logical form xRy:

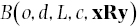
We now, however, face a new problem of how to explain the status of xRy. If it is a constituent of the judgment, then we will need to know what relates this to the other constituents in such a way that it can furnish the complex with the correct order. But this question will just lead us headlong onto a regress much the same as that considered previously with regard to the original problem of the unity of the proposition. Russell’s (1913/84, p.118) diagram of the structure of judgment makes it clear that the logical form is a constituent of the judgment, though he does not think that they are constituents of the facts they correspond to.

5 The Wide Direction Problem (WD)

Wittgenstein’s criticisms were clearly focused on this problem, viz., WD. WD can be seen as an extension of ND. ND shows that the subordinate relation is not a relating relation. But, if it is just another term of the primary relation, why should its relational status survive at all? If the subordinate relation is really just another “brick,” not “cement,” in other words, we will be unable to distinguish a judgment‐complex as being of the form

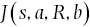
rather than being of the form

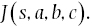
As Wittgenstein puts it (albeit with use of an example having a slightly different logical form), there is nothing in the MRTJ to show that there is anything wrong with the “judgement” that “this table penholders the book” (NL 96). Thus Russell’s theory is unable to account for the difference between sense and nonsense. Wittgenstein’s point, and with it the distinction between ND and WD, can be summarized very clearly:

ND shows MRTJ cannot account for the difference between Othello’s belief that Desdemona loves Cassio and Othello’s belief that Cassio loves Desdemona.

WD shows MRTJ cannot distinguish between those possible beliefs of Othello’s and his nonsensical pseudo‐belief that Love desdemonas Cassio.

6 Wittgenstein’s Objection and Russell’s Paralysis

As mentioned above, Russell was reportedly “paralysed” by Wittgenstein’s objection to the MRTJ (Wittgenstein, letter to Russell, 22 July 1913). In the absence of sufficient surviving correspondence between Russell and Wittgenstein from the relevant period to explain Russell’s response, the challenge of determining what led Russell to react this way has proved difficult to resist for many Russell scholars. It is hardly satisfactory to rest content with the objection as phrased by Wittgenstein in the Tractatus as providing illumination on the issue. “The correct explanation of the form of the proposition, ‘A makes the judgement p,’” Wittgenstein announces, “must show that it is impossible for a judgement to be a piece of nonsense.” And, he adds in parentheses: “Russell’s theory does not meet this requirement” (TLP 5.5422). However, it is far from clear from this why a theory of judgment should meet this condition. Wittgenstein himself, it might be thought, ought to recognize that at least some of the propositions he holds to be nonsensical in the Tractatus al least appear to be believed by at least some people who don’t recognize them as nonsensical (Griffin, 1985, p.240; 1986, p.144 – it should be noted, of course, that Wittgenstein himself consistently maintained that nonsense cannot be believed). At least on the face of it, then, a correct descriptive theory of judgment should make it possible for a judgment to be a piece of nonsense. Otherwise it will have failed to adequately describe the actual forms that judgments can take. The objection, and how it led to Russell’s paralysis, clearly needs some further unpacking.

Attempts to decipher the exact nature of Wittgenstein’s objections and the precise reason why Russell abandoned the MRTJ have diverged from one another dramatically, as is unsurprising given the poverty of evidence available to support any interpretation. However, following the influential interpretation offered by Stephen Sommerville and Nicholas Griffin, it has become fairly well accepted that the fatal blow to the MRTJ hinged on an incompatibility between the MRTJ and the theory of types (notable dissenters to this view are Landini, 1991; and Pincock, 2008). According to Sommerville (1981) and Griffin (1985; 1986), Russell has no choice but to accept the “no nonsense” criterion forwarded by Wittgenstein because this criterion is demanded of the MRTJ if it is to remain consistent with the theory of types. As mentioned above, the MRTJ is intended to play a central role in the justification of the hierarchy of orders required by ramified type‐theory. Detailed consideration of type‐theory is found below but, at this point, it suffices to remind ourselves that the theory is commonly thought of as an attempt to outlaw certain “nonsensical” formations. If the MRTJ is going to lend support to such a theory then, evidently, Wittgenstein’s criterion must have at least some relevance: judgments must be well formed by the strictures of type‐theory if the theory of types is not to be doomed from the outset, hence WD will need to be solved if the MRTJ is to churn out judgments that do not run into direct conflict with type‐theory. But, in that case, Sommerville and Griffin think, further reflection on Wittgenstein’s criterion reveals a horrendous problem for Russell.

The only solution to WD (according to Sommerville and Griffin) seems to be to appeal to a distinction in type between the subordinate relation – L and R in our examples – and the other objects of the primary relation of a judgment‐complex. That Wittgenstein drew this moral is strongly suggested in the following letter to Russell:

If I analyse the prop[osition] Socrates is mortal into Socrates, Mortality and (∃x,y)ε₁(x,y) I want a theory of types to tell me that ‘Mortality is Socrates’ is nonsensical, because if I treat ‘Mortality’ as a proper name (as I did) there is nothing to prevent me to make the substitution the wrong way round.

(Letter to Russell, 16 January 1913)

The problem as Griffin and Sommerville see it, however, is that although one wants a theory of types to preserve the theory of judgment, one first needs the theory of judgment to generate the theory of types. In short, this “solution” to WD puts things hopelessly back to front. If the MRTJ generates and provides the philosophical justification for the theory of types, we cannot presuppose type‐theory when setting out the MRTJ.

Viewed in this way, Russell’s paralysis is unsurprising: Wittgenstein’s criticisms go right to the foundations of Principia, leaving the philosophical justification of ramified type‐theory in tatters. Sommerville and Griffin’s interpretation has firmly established the view that the collapse of the MRTJ is, at least in part, determined by its connections with the theory of types. However, even if one agrees with them about this, the interpretation of Wittgenstein’s criticisms does not end there. Consider the form in which their interpretation of the situation is given in the following passage from Griffin:

Why won’t Wittgenstein allow us to make these stipulations [regarding the type of the constituents of judgment‐complexes]? Because to make them would require further judgements. We are trying to analyze what is supposed to be the simplest type of elementary judgement. But to do so would seem to involve us in yet further judgements. Moreover the further judgements required are of an extremely problematic character. For to judge that a and b are suitable arguments for a first‐order relation is to make a judgement of higher than first‐order. Yet, as Russell makes quite clear in Principia (pp.44–6), higher‐order judgements are to be defined cumulatively on lower‐order ones. Thus we cannot presuppose second‐order judgements in order to analyze elementary judgements.

(Griffin, 1986, p.144)

There is, I think, both something right and something wrong about this interpretation. It is right to recognize the connection between MRTJ and type‐theory as the source of the former theory’s difficulty. It is wrong, however, to see this problem as involving a regress of judgments or as an epistemological problem. As the MRTJ is clearly the centerpiece of Russell’s epistemology, it is easy to be led astray into thinking that the conflict with type‐theory must also occur at the epistemological level. I will call this interpretation the epistemological interpretation (EI). I think there are two fundamental problems with EI that show it to be false. After illustrating these, I will go on to suggest my own ontological interpretation (OI) as a solution to these two problems. (EI) and (OI), more precisely defined, are as follows:

(EI) is the view that Wittgenstein’s criticisms exposed an incompatibility between Russell’s epistemology and his theory of types in the sense that the theory of types is justified by Russell’s epistemology (in particular the epistemic relation of judgment as analyzed by the MRTJ), yet the MRTJ relies on a theory of types. Thus the theory of types and the MRTJ cannot be rendered compatible with one another without circularity.

(OI) is the view that Wittgenstein’s criticisms exposed an incompatibility between Russell’s ontology and his theory of types in the sense that the theory of types is justified by the MRTJ and the MRTJ relies on treating all elements of a judgment as being of the same ontological type, while imposing order distinctions within the epistemic domain of judgments. Yet it is impossible to answer Wittgenstein’s objection without imposing ontological type distinctions on judgments.

I will explain OI in detail shortly. First, the two problems with EI are:

EI conflates the roles of the MRTJ and the so‐called direct inspection argument (explained below) in Principia.
EI overlooks the importance of the role played by the logical status of the subordinate relation in a judgment‐complex in WD.

Let us look at each problem in turn.

7 Direct Inspection and the MRTJ (First Problem with EI)

If EI is correct, then the incompatibility of type‐theory and the MRTJ arises because, in order to avoid nonsensical judgments, we must first judge that the constituents of our judgments are of the requisite types. But, as Griffin says in the passage quoted above, we cannot presuppose such judgments when making elementary judgments, if we are to appeal to a hierarchy of judgments that places elementary judgments at the most fundamental level. If the lowest level of the hierarchy depends on judgments that can only be reached at a higher level of the hierarchy, then such judgments cannot be available after all and the entire project seems doomed. This story, central to EI, rests on a misconception about type‐theory, however. For the kinds of distinctions needed to guard against WD are not distinctions that require us to traverse the hierarchy of judgments in order to secure them.

The formal language contained in Principia is stratified with respect to two distinct hierarchies: the hierarchy of types and the hierarchy of orders. The type hierarchy yields “simple type‐theory”; when combined with the order hierarchy, it yields “ramified type‐theory.” Simplifying matters somewhat, the type hierarchy assigns a type to a function determined by the type of the arguments it can meaningfully apply to, while the order hierarchy assigns an order to a function determined by the range of any quantifier used to define it, as summed up by the vicious circle principle: “Whatever involves all of a collection must not be one of the collection” (Whitehead and Russell, 1910, p.37).

Historically, the relationship between the two hierarchies has been shrouded in mystery. Russell himself did not distinguish the two hierarchies in a clear way, often appearing to be appealing to the vicious circle principle as the justification of both hierarchies. Ramsey first urged the separation of the two, which he suggested had only been unified in Principia by virtue of “being both deduced in a rather sloppy way from the ‘vicious circle principle’” (Ramsey, 1925, p.24). Gödel agreed that the simple theory of types “is entirely independent of [the hierarchy of orders] and has nothing to do with the vicious circle principle” (Gödel, 1944, pp.134–5).

Let us briefly clarify the workings of ramified type‐theory so as to be as clear as possible about the alleged impact of WD on that theory that is proposed by EI. The simplest way to understand the theory of types is to momentarily overlook Russell’s doubts (explained in the next paragraph) about the reality of classes and begin by recognizing a hierarchy dictating membership restrictions on classes. A class can only be a member of a class of higher type. So the class of philosophers can be a member of a class of classes but not of a class of people. This is not an observation about the truth conditions of such claims, but a restriction on the very admissibility of those claims. The claim that the class of philosophers is a member of the class of people is not false in the formal language of type‐theory; it is inexpressible within the grammar of the language. Type‐restrictions, in other words, add to the formation‐rules of the language to restrict what counts as a well‐formed formula.

Now, Russell and Whitehead insist that the formal language of Principia Mathematica is a “no‐classes” theory, so the above sketch needs revision when applied to their version of type‐theory. The items subject to type‐restrictions in their system are propositional functions. So we will say that propositional functions are stratified into a hierarchy determining which functions can be functions of which arguments. The easiest way to (very roughly) grasp this is by analogy with predication – the predicate “is a person” cannot be predicated of the predicate “is a philosopher,” for example. We can make this clearer by symbolizing type‐indices as subscripts on function variables as follows:

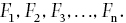
We then specify that a function of type n may only be argument to a function of type n + 1. This will be sufficient to ensure that the propositional‐function version of Russell’s paradox is banished from the formal system. But the above hierarchy is only half of the story of Principia’s type‐theory. Russell was convinced that the full defense of logicism should solve all of the paradoxes (including those we now recognize as semantic rather than merely logical). But consider the Epimenides paradox, otherwise known as the Cretan Liar Paradox, which we assume to be uttered by the Cretan, Epimenides:

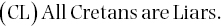
(CL) is contradictory if we assume that all utterances made by Cretans prior to Epimenides’ utterance of (CL) were indeed lies. Yet (CL) does not violate the above hierarchy in any way. An additional diagnosis is needed here, and Russell’s proposal is that we recognize a second hierarchy which is the outcome of the “vicious circle principle,” according to which no statement made about a given totality can itself be a member of that totality. Epimenides violates this principle when he seeks to make a claim about the totality of utterances made by Cretans using a statement which itself adds to that totality. To avoid such violations, we must now impose a second hierarchy on top of the previous hierarchy of functions. To distinguish the two (a distinction which Russell only imperfectly respected in his own formulation), we will call the first hierarchy the hierarchy of types. This hierarchy by itself is the hierarchy of simple type‐theory. If we add a hierarchy restricting statements concerning totalities as just outlined, we will call this the hierarchy of orders. The addition of this hierarchy to simple type‐theory, yields ramified type‐theory. In ramified type‐theory, every level of the type hierarchy further divides into a hierarchy of orders (thus every level of types branches, or ramifies, into orders). We can add superscripts to our already subscripted (for type) expressions to display their orders. The expression “F_n^m,” for example can only be argument to an expression of the right type and order, such as “G_n+1^m+1.”

Without going too far into the formal details of this baroque edifice, we can note that the two hierarchies have quite independent justifications, and that only the hierarchy of orders is justified by appeal to the vicious circle principle. This in turn is unquestionably linked to the MRTJ as Russell and Whitehead explicitly argue that the hierarchy of orders has its origins in the recognition that the MRTJ leads to a hierarchy of orders of truth (Whitehead and Russell, 1910, p.42). Justification for the hierarchy of types (as opposed to orders), however, must come from elsewhere. Russell and Whitehead offer the “direct inspection” argument as justification for the imposition of this hierarchy: direct inspection of the nature of a propositional function is supposed to reveal that

not only is it impossible for a function φû to have itself or anything derived from it as argument, but that, if ψû is another function such that there are arguments a with which both ‘φa’ and ‘ψa’ are significant, then ψû and anything derived from it cannot significantly be argument to φû.

(Whitehead and Russell, 1910, p.47)

The direct inspection argument, puzzling to interpret though it is, clearly has nothing whatsoever to do with acts of judgment. It is an argument to the effect that direct inspection of a propositional function will reveal it to have a logical type. The argument concerns the significance of propositional functions, and is intended to justify the hierarchy of types by showing how consideration of the range of significance of a function naturally leads to a division in logical types among functions. It is not our making a judgment that introduces the type – the type is presumably already there for us to discover on inspection. Types, in short, can be fixed prior to, and wholly independently of, judgments and the fixing of their orders. But, in that case, EI offers no explanation for the severity of Wittgenstein’s objection after all: we can simply help ourselves to a theory of types in order to solve WD without embroiling ourselves in any circularity so long as we do not appeal to the hierarchy of orders. We would thereby ensure that the MRTJ meets Wittgenstein’s criterion of excluding nonsense without any further problem. Thus EI fails to explain what was wrong with the MRTJ.

8 The Logical Status of the Subordinate Relation (Second Problem with EI)

The importance of the subordinate relation in understanding where the MRTJ goes wrong can be illustrated by briefly considering a set of distinctions drawn by Miller (2006) in his diagnosis of the MRTJ’s demise. Miller suggests that Russell’s favored solution to the direction problem (he does not specify whether wide or narrow) involved distinguishing the “object‐terms” from the “object‐relation” of a judgment‐complex. Let j = B(o,d,L,c); then d and c are object‐terms, and L is an object‐relation (as they are the terms and relation of Othello’s belief). The main problem with Miller’s account of the MRTJ is its failure to take seriously the following question: if B is simply a 4‐place relation, what gives L any special status? Miller does not address this problem. But no account of why Russell abandoned the theory can afford to ignore it. To do so is to miss the whole force of WD. Indeed we can see this if we consider what would happen were Miller’s analysis given in response to WD. It would clearly beg the question against the objection by presupposing a solution to WD in the analysis of j: we cannot help ourselves to the distinctions posited in Miller’s analysis until we have a solution to the direction problems. If L is a brick in the structure of j, rather than the cement of j, there can be no way of determining if L is an object‐term or object‐relation. In short: Miller’s analysis fails to account for WD.

What is the relevance of this fault in Miller’s analysis to EI? What it shows is that there is a feature unique to MRTJ, missing from Miller’s account, which is intrinsically tied up with the status of the subordinate verb. This is clear enough when we consider that there is no equivalent to WD in the early case of the problem of the unity of the proposition. Desdemona cannot be a relation on Russell’s (1903) theory of propositions, as Russell there draws a (perhaps questionable) distinction between things that can only be the relata of properties and relations, and “concepts” (embracing properties and relations) which have a “two‐fold status” enabling them to occur as both relata of relations and as relating‐relations. But, such a distinction cannot be drawn in the MRTJ: when relations are occurring as terms of other relations (as they are when they are subordinate relations in judgment‐complexes) they are logically on a par with all the other terms and, therefore, a distinction between individuals and relations will be no help. Even if relations do retain a twofold status, occurring either as relating relations or as subordinate relations, they are not relating‐relations when they occur as subordinate ones. Thus, whatever holds for the subordinate relation in j, holds for everything related by the primary relation of j.

Now notice that, most importantly for the present discussion, this has nothing whatsoever to do with epistemology. Again, we should not be misled by the fact that we are discussing the analysis of judgments into thinking that the problem we have located is an epistemological one. The important point is simply that, in the above example, L is a term of a relation, not a relating‐relation – and that is an ontological (or perhaps logical) distinction, not an epistemological one. EI has nothing to say about it.

These two problems leave EI looking deeply unconvincing as an account of the downfall of the MRTJ. Another answer is needed if we are to determine exactly what was wrong with the theory. I will now propose an answer.

9 Solution to these two Problems: OI

What the above objections to EI reveal is that the clash between the MRTJ and the theory of types cannot have occurred at the level of Russell’s epistemology if it was really responsible for his rejection of the MRTJ. Where then did it occur? The answer is, I suggest, clearly given in Wittgenstein’s letters to Russell discussing the MRTJ. Perhaps the most explicit is the following comment: “I think that there cannot be different types of things! In other words whatever can be symbolized by a simple proper name must belong to one type” (16.1.13, NL, p.121). This is not an objection to Russell’s epistemology, but to his ontology. It is Russell’s ontology that is drawn into conflict with the theory of types by the MRTJ. The MRTJ makes two mutually exclusive demands on judgments. On the one hand, all relata of the primary relation must be terms of the same logical type (bricks, not cement) if they are to be related by the primary relation. But, in order to capture the difference between well‐formed judgments and nonsense like “Love desdemonas Cassio,” a special status must be bestowed on the subordinate relation. Only the theory of types can salvage the MRTJ. But to do that, it must apply directly to the entities in the world that are the constituents of judgments: only an ontological theory of types will do the trick.

Why would the imposition of an ontological theory of types be problematic for Russell? After all, we have seen that there is no circularity involved in appealing to the theory of types in order to solve WD. Why would Russell be so concerned by the problem? To answer this question, we need to consider one final elusive aspect of Russell’s philosophy, namely the ontology he envisaged for Principia’s ramified type‐theory.

10 Propositional Functions

Principia’s type‐theory applies to what Whitehead and Russell call “propositional functions,” stratifying them into a hierarchy whereby a propositional function can only be applied to a function below it in the hierarchy. But much discussion has centered on what Whitehead and Russell took the precise nature of propositional functions to be. Traditionally the theory has been assumed to operate at the level of Russell’s ontology, arranging the constituents of mathematical reality into types (Quine, 1953; 1966). However, as several commentators have pointed out, this interpretation does not sit comfortably with the philosophical introduction to Principia. There, as in later works, Russell is insistent that the things subject to type‐distinctions, namely propositional functions, are linguistic items. Thus it often seems that Russell envisages type‐theory as operating merely at the level of the linguistic expression of mathematical truths, not at the level of whatever entities those truths are about and, furthermore, it seems that he holds this to be central to the philosophical justification of the theory of types. For example, he is adamant in correspondence with Wittgenstein after reading the Tractatus that “the theory of types is […] a theory of correct symbolism” (see Wittgenstein, Letter to Russell, 19 August 1919).

In the informal exposition of the intended interpretation of the formal system of Principia, as just noted, Whitehead and Russell speak as if predicate variables stand for things called “propositional functions.” If propositional functions are understood along the same lines as they feature in the Principles of Mathematics, the traditional interpretation seems to be right. There, propositional functions are as much a part of Russell’s ontology as propositions are. Taking propositional functions to be of this sort guarantees that the theory of types is an ontological theory, despite Whitehead and Russell’s apparent statements to the contrary.

A number of problems face this traditional way of interpreting Principia. For one thing, the interpretation is in the unfortunate position of being openly contradicted by one of the authors of the work it is intended to interpret. Russell, in My Philosophical Development, explicitly states that propositional functions are linguistic entities only: “A propositional function is nothing but an expression. It does not, by itself, represent anything. But it can form part of a sentence which does say something, true or false” (Russell, 1959, p.69). Admittedly, this passage cannot be taken as conclusive evidence of Russell’s position, as he contradicts himself awkwardly on this issue (and others) in My Philosophical Development (1959, p.68). But more reliable sources contain similar claims. For example, in “The Philosophy of Logical Atomism” (1918), Russell is explicit in his denial of the existence of propositional functions as entities: “A propositional function is nothing, but, like most of the things one wants to talk about in logic, it does not lose its importance through that fact” (Russell, 1918, p.202). However, it should be noted that even this source is written after Principia and so cannot be deemed decisive. Secondly, and more importantly, however, Principia (officially, at least) lacks the ontological resources to support an ontological hierarchy of types. Propositions are rejected in Principia in line with the adoption of the MRTJ. But this now poses a serious problem for the interpretation we have been considering, as we can see if we look at how Whitehead and Russell describe functions in Principia:

Let φx be a statement containing a variable x and such that it becomes a proposition when x is given any fixed determined meaning. Then φx is called a ‘propositional function’; it is not a proposition, since owing to the ambiguity of x it really makes no assertion at all.

(Whitehead and Russell, 1910, p.14)

By a ‘propositional function’ we mean something which contains a variable x, and expresses a proposition as soon as a value is assigned to x. That is to say, it differs from a proposition solely by the fact that it is ambiguous: it contains a variable of which the value is unassigned.

(Whitehead and Russell, 1910, p.38)

The problem with this talk of propositional functions “becoming” or “expressing” a proposition upon the assignment of a value to x is that this means, according to the official ontology of Principia, there is nothing for a propositional function to become under such circumstances. Propositions just don’t exist.

Perhaps there is no conclusive evidence for either interpretation of Principia. The authors of that work, it seems, were simply not clear enough in what they said on the matter. However, I propose that reflection on Wittgenstein’s criticisms of Russell’s MRTJ helps to resolve this debate, since it provides compelling evidence that Russell was anxious to avoid the very ontological type‐distinctions that the traditional interpretation of Principia attributes to him.

The traditional interpretation of propositional functions gives entirely the wrong prediction regarding Russell’s response to Wittgenstein’s objection. In fact, it predicts that Russell would not be at all troubled, let alone paralyzed, by the objection. If the traditional interpretation were correct, then Russell’s paralysis would be no more explicable by OI than it was by EI. For it would arm Russell with the mechanism to block the formation of nonsensical judgments with ease. All that is needed to block the objection is an ontological theory of types, which assigns a special status to the subordinate relation. Why Russell should respond in the way that he did to Wittgenstein’s objection is therefore utterly inexplicable if OI is coupled with a traditional interpretation of the theory of types.

When on the other hand, the linguistic interpretation of the theory of types is coupled with OI, Russell’s paralysis becomes fully explicable: OI demonstrates that the solution to WD is incompatible with a linguistic interpretation of the predicate expressions of Principia. Unless universals divide into types (i.e., unless propositional functions and universals are identified), the theory of types cannot help with WD. It is not expressions that are the terms of the primary relation in a judgment‐complex; it is the individuals and relations that the judgment is about. Hence, no theory of types will be able to play a role in solving WD until it applies to those individuals and relations also. The linguistic interpretation holds that the primary motivation for the version of type‐theory it attributes to Principia was the authors’ desire to avoid imposing type restrictions onto the ontology of the work. A demonstration from Wittgenstein that Russell’s attempt to avoid ontological type‐restrictions could only succeed if it were to presuppose the very restrictions it is designed to avoid, makes Russell’s reaction unsurprising. Thus the linguistic interpretation, unlike the traditional interpretation, of propositional functions explains Russell’s paralysis.

11 Wittgenstein on Logical Form

The above discussion is intended to provide an explanation of Russell’s paralysis, i.e., his response to Wittgenstein’s objections. But it would be a mistake to assume that what paralyzed Russell was also the main concern of Wittgenstein. Wittgenstein was not concerned to mount a defense of ramified type‐theory, nor was he particularly interested in the details of the theory as manifested in Principia. That much is clear from the brief and characteristically cryptic “disposal” of Russell’s paradox offered at TLP 3.333 (cf. Chapter 17, LOGIC AND THE TRACTATUS). Whatever interpretation one might want to offer of this passage, it is certainly obvious that Wittgenstein did not think a theory of types was required for the solution of the paradox. And, of course, by implication this means that the theory is wholly redundant; for it has no other purpose beyond the solution of this and related paradoxes. Indeed, Wittgenstein thinks that “the whole of the ‘theory of types’” (TLP 3.331) can be summarized by the observation that “No proposition can make a statement about itself because a propositional sign cannot be contained in itself” (TLP 3.332).

If Russell’s paralysis was caused by the impact of Wittgenstein’s objection on the theory of types, then that is likely to have been collateral damage and not the main target of Wittgenstein’s own thoughts. While there is of course no reason to think that Wittgenstein would not have raised an objection to Russell’s theory just as an end in itself, examination of the correspondence between the two from the period in question strongly suggests that Wittgenstein’s objection arose as an upshot of the development of his own ideas, and these were certainly not aimed at type‐theory. It is true that Wittgenstein was devoting some sort of attention to the theory of types in 1913. He reported to Russell that he was “thinking about the beastly theory of types” in September of 1913 (NL 122). This may tempt us to think that he was more interested in the details of type‐theory in 1913 than he was when he completed the Tractatus five years later. However, the following discussion of types between Russell and Wittgenstein shows that Wittgenstein had already arrived at the view expressed in TLP 3.332 by mid‐January of 1913:

All theories of types must be done away with by a theory of symbolism showing that what seem to be different kinds of things are symbolized by different kinds of symbols which cannot possibly be substituted in one another’s places.

(NL 121)

When one scrutinizes the discussions of the theory of types in the correspondence between the two, there is scant evidence that Russell and Wittgenstein ever really managed to talk about the same thing. Wittgenstein showed no real interest in the formal aspects of the theory, and Russell never seemed to fully understand Wittgenstein’s view on types, much to the latter’s frustration. Even by the time Russell had read the finished manuscript of the Tractatus, his response to Wittgenstein’s criticisms of the theory of types clearly missed Wittgenstein’s intended point. Russell defended the theory by explaining that it was “a theory of correct symbolism: a simple symbol must not be used to express anything complex: more generally, a symbol must have the same structure as its meaning,” to which a seemingly exasperated Wittgenstein retorted:

That’s exactly what one can’t say. You cannot prescribe to a symbol what it may be used to express. All that a symbol can express it may express. This is a short answer but it is true!

(Letter to Russell, 19 August 1919)

If Wittgenstein’s attack on type‐theory was not understood by Russell by 1919, it clearly cannot have been the cause of his paralysis in 1913. Thus it seems clear that the impact on types that Russell took the theory to have was not the intended target of Wittgenstein’s objection.

To understand Wittgenstein’s intention we have to see how these kinds of ideas fit into the overall account of logic and propositional structure on offer in the Tractatus. While it is true that much of that book is inspired (either as a source of agreement or disagreement) by Russell, we cannot overlook the other of Wittgenstein’s great influences, namely Frege (see Chapter 4, WITTGENSTEIN AND FREGE). Frege’s distinction between concept and object and his hierarchy of concepts (which Russell acknowledged as a forerunner of his own theory of types) are obviously relevant to the discussion of types in the Tractatus. Most importantly, I think, this proto‐“type theory” of Frege’s is offered as a solution to a very different problem to the one Russell’s theory addresses. Frege’s hierarchy is his proposed solution to the problem of the unity of the proposition rather than to set‐theoretic or semantic paradoxes. This concern is inherited by Wittgenstein in the Tractatus and provides the link between Wittgenstein’s discussion of types and his objection to the MRTJ.

For Frege, the explanation of how the parts of an atomic proposition combine to form a unity is to be found in his distinction between concept and object. There is a fundamental difference between two different types of entity in the realm of reference: the complete entities (objects) and the incomplete entities (concepts). The incompleteness of the latter can only be resolved by their combination with the former, and only when these two kinds combine (or when a similar combination is effected between concepts of different levels in the hierarchy in the case of nonatomic propositions) can a proposition be produced. Propositions (Fregean thoughts) reside in the realm of sense, not reference, but their combination reflects and depends on this mode of combination between elements in the realm of reference, as Fregean thoughts are modes of presentation of truth values. These values occur in the realm of reference as the values of concepts, which are construed as functions whose values are always truth values. The distinctions at play are, according to Frege, fundamental features of reality, “deep in the nature of things” (Frege, [1891] 1952/80, p.41).

Wittgenstein sees a deep insight in Frege’s distinction but rightly rejects the appeal to brute metaphysical facts as a ground for the distinction. If one is seeking a solution to the unity of the proposition, it is not enough to state that propositions are unities because of distinctions deep in the nature of things. The problem is a serious objection to the claim that propositions exist on the grounds that how their constituents combine to form something propositional is mysterious. Embracing this mystery as inexplicable is hardly a satisfactory response to that objection.

Wittgenstein’s proposal in the Tractatus is to relocate Frege’s distinction within a new theory of propositional content, namely the picture theory of the proposition (cf. Chapter 8, THE PICTURE THEORY, and Chapter 32, WITTGENSTEIN ON INTENTIONALITY). According to this theory, what distinguishes propositions from mere collections of their constituents is that in a proposition the elements are arranged in a pictorial form. An often‐overlooked feature of the picture theory is the appeal made to the use that elements of the picture are put to in explaining this pictorial form:

In order to recognize a symbol by its sign we must observe how it is used with a sense. A sign does not determine a logical form unless it is taken together with its logico‐syntactic employment.

(TLP 3.326–3.327)

A proposition, for Wittgenstein, is a logical picture of facts (TLP 3). But to picture a fact simply is to use the elements of the picture in the right kind of way (see also Chapter 23, MEANING AND UNDERSTANDING). This is the fundamental insight Wittgenstein sees in the picture theory, revealed by his first thoughts on the subject in his reflections on the use of models to represent facts (see e.g., NB 29.9.14). Accordingly, what makes a sentence nonsensical is not something we can prescribe against independently of the use of the sentence (as for example, the theory of types attempts to do), but simply that we have failed to use the sentence to picture something. This claim was fundamental to the picture theory from its earliest inception:

Let us remember the explanation why “Socrates is Plato” is nonsense. That is, because we have not made an arbitrary specification, NOT because a sign is, shall we say, illegitimate in itself!

(NB 22.8.14)

This view remains central to the theory in the Tractatus (5.473) and lies behind Wittgenstein’s insistence that the theory of types is dispensable. Wittgenstein’s brief “disposal” of Russell’s paradox in the Tractatus is based on the following passage:

The reason why a function cannot be its own argument is that the sign for a function already contains the prototype of its argument, and it cannot contain itself.

For let us suppose that the function F(fx) could be its own argument: in that case there would be a proposition ‘F(F(fx))’, in which the outer function F and the inner function F must have different meanings, since the inner one has the form φ(fx) and the outer one has the form ψ(φ(fx)). Only the letter ‘F’ is common to the two functions, but the letter by itself signifies nothing.

(TLP 3.333)

The letter “F” by itself signifies nothing because it signifies only when it is used in a proposition. In other words, it signifies only when it is used as an element in a picture. But to attempt to use the letter in a proposition picturing the application of a function to itself is impossible, because any such attempt must use the letter in two different ways. But once the way in which it is used differs, the logical form thereby automatically differs because that logical form is determined by the use (TLP 3.327).

We can see quite clearly how the “theory of types” is being made redundant on the above theory of propositions as pictures. But the theory of types in question is more recognizable as Frege’s hierarchy of concepts than Russell’s ramified type‐theory of Principia Mathematica. What Wittgenstein offers us is an account of the sorts of distinctions that Frege appeals to in order to explain the unity of the proposition but one that attempts to give a full explanation for why such distinctions exist, rather than resting content with positing them as metaphysical limitations on propositional structure. This was what interested Wittgenstein about the theory of types, not the details of the theory as it fitted into the formal apparatus of Principia Mathematica.

12 Conclusion

I have attempted to explain some of the complex philosophical interactions between Russell and the early Wittgenstein in a way that respects the insights of each and the different projects each were embarked on. There is no doubt that, at one stage, the two saw themselves as working together on a common project. But it is equally obvious that their two projects diverged quite dramatically in the end. Great philosophers respond to those who inspire them in original ways, developing new and exciting views of their own that often pursue very different concerns to those of the work that influenced them. Such was the case here. As time passed their projects drifted further and further apart. But there can be no question that their mutual influence on each other during the period of Wittgenstein’s first philosophy was of profound importance to the development of the work of each. Understanding the work of either during this period requires careful study of the other.

References

Frege, G. ([1891] 1952/80). Function and Concept. Translation in G. Frege. Translations from the Philosophical Writings of Gottlob Frege. Ed. P. Geach and M. Black. Third edition. Oxford: Blackwell. (Original work published 1891.)
Gödel, K. (1944). Russell’s Mathematical Logic. In P.A. Schilpp (Ed.). The Philosophy of Bertrand Russell (pp.123–153). London: Harper and Row.
Griffin, N. (1985). Russell’s Multiple Relation Theory of Judgement. Philosophical Studies, 47, 213–241.
Griffin, N. (1986). Wittgenstein’s Criticisms of Russell’s Theory of Judgement. Russell, 4, 132–145.
Landini, G. (1991). A New Interpretation of Russell’s Multiple‐Relation Theory of Judgement. History and Philosophy of Logic, 12, 37–69.
Miller, A. (2006). Russell, Multiple Relations, and the Correspondence Theory of Truth. The Monist, 89, 85–101.
Monk, R. (1990). Ludwig Wittgenstein: The Duty of Genius. London: Jonathan Cape.
Pincock, C. (2008). Russell’s Last (and Best) Multiple‐Relation Theory of Judgement. Mind, 117, 107–139.
Quine, W. (1953). Logic and the Reification of Universals. In W. Quine. From a Logical Point of View (pp.102–129). Cambridge, MA: Harvard University Press.
Quine, W. (1966). Russell’s Ontological Development. Journal of Philosophy, 63, 657–667.
Ramsey, F.P. (1925). The Foundations of Mathematics. Reprinted in F.P. Ramsey. (1931). The Foundations of Mathematics and other Logical Essays (pp.1–61). Ed. R.B. Braithwaite. London: Routledge.
Russell, B. (1901). Part I of the Principles, Draft of 1901. Edited in G.H. Moore (Ed.). (1994). The Collected Papers of Bertrand Russell (Vol. 3): Toward the Principles of Mathematics, 1900–1902. London: Routledge.
Russell, B. (1903). The Principles of Mathematics. Cambridge: Cambridge University Press.
Russell, B. (1912). The Problems of Philosophy. Oxford: Oxford University Press.
Russell, B. (1913/84). Theory of Knowledge: The 1913 Manuscript. Ed. E.R. Eames. London: George Allen and Unwin.
Russell, B. (1918). The Philosophy of Logical Atomism. Reprinted in R.C. Marsh (Ed.). (1956). Logic and Knowledge: Essays 1910–1950 (pp.177–281). London: George Allen and Unwin.
Russell, B. (1959). My Philosophical Development. London: Routledge.
Sommerville, S. (1981). Wittgenstein to Russell (July, 1913): “I am very sorry to hear … my objection paralyses you.” In R. Haller and W. Grassl (Eds). Language, Logic and Philosophy (pp.182–188). Vienna: Hölder‐Pichler‐Tempsky.
Whitehead, A.N. and Russell, B. (1910). Principia Mathematica (Vol. 1). Cambridge: Cambridge University Press.