Secondary Electrons

3.1 Origin

Secondary electrons (SE) are created when inelastic scattering of the beam electrons ejects weakly bound valence electrons (in the case of ionically or covalently bonded materials) or conduction band electrons (in the case of metals), which have binding energies of ~ 1–15 eV to the parent atom(s). Secondary electrons are quantified by the parameter δ, which is the ratio of secondary electrons emitted from the specimen, N_SE, to the number of incident beam (primary) electrons, N_B:

$\delta ={N}_{SE}/{N}_B$

(3.1)

3.2 Energy Distribution

The most important characteristic of SE is their extremely low kinetic energy. Because of the large mismatch in relative velocities between the primary beam electron (incident energy 1–30 keV) and the weakly bound atomic electrons (1–15 eV ionization energy), the transfer of kinetic energy from the primary electron to the SE is relatively small, and as a result, the SE are ejected with low kinetic energy. After ejection, the SE must propagate through the specimen while undergoing inelastic scattering, which further decreases their kinetic energy. SE are generated along the complete trajectory of the beam electron within the specimen, but only a very small fraction of SE reach the surface with sufficient kinetic energy to exceed the surface energy barrier and escape. The energy spectrum of the secondary electrons that escape is peaked at only a few eV, as shown in ◘ Fig. 3.1a for a measurement of a copper target and an incident beam energy of E₀ = 1 keV. Above this peak, the intensity falls rapidly at higher kinetic energy (Koshikawa and Shimizu 1973). ◘ Figure 3.1b shows the cumulative intensity as a function of energy: 67 % of the secondary electrons from copper are emitted with less than 4 eV, and 90 % have less than 8.4 eV. Secondary electron production is considered to cease for kinetic energies above 50 eV, an arbitrary but reasonable value considering how sharply the energy distribution of ◘ Fig. 3.1a is skewed toward low energy. Inspection of the literature of secondary electrons confirms that the distribution for copper is generally representative of a large range of metals and other materials (e.g., Kanaya and Ono 1984).

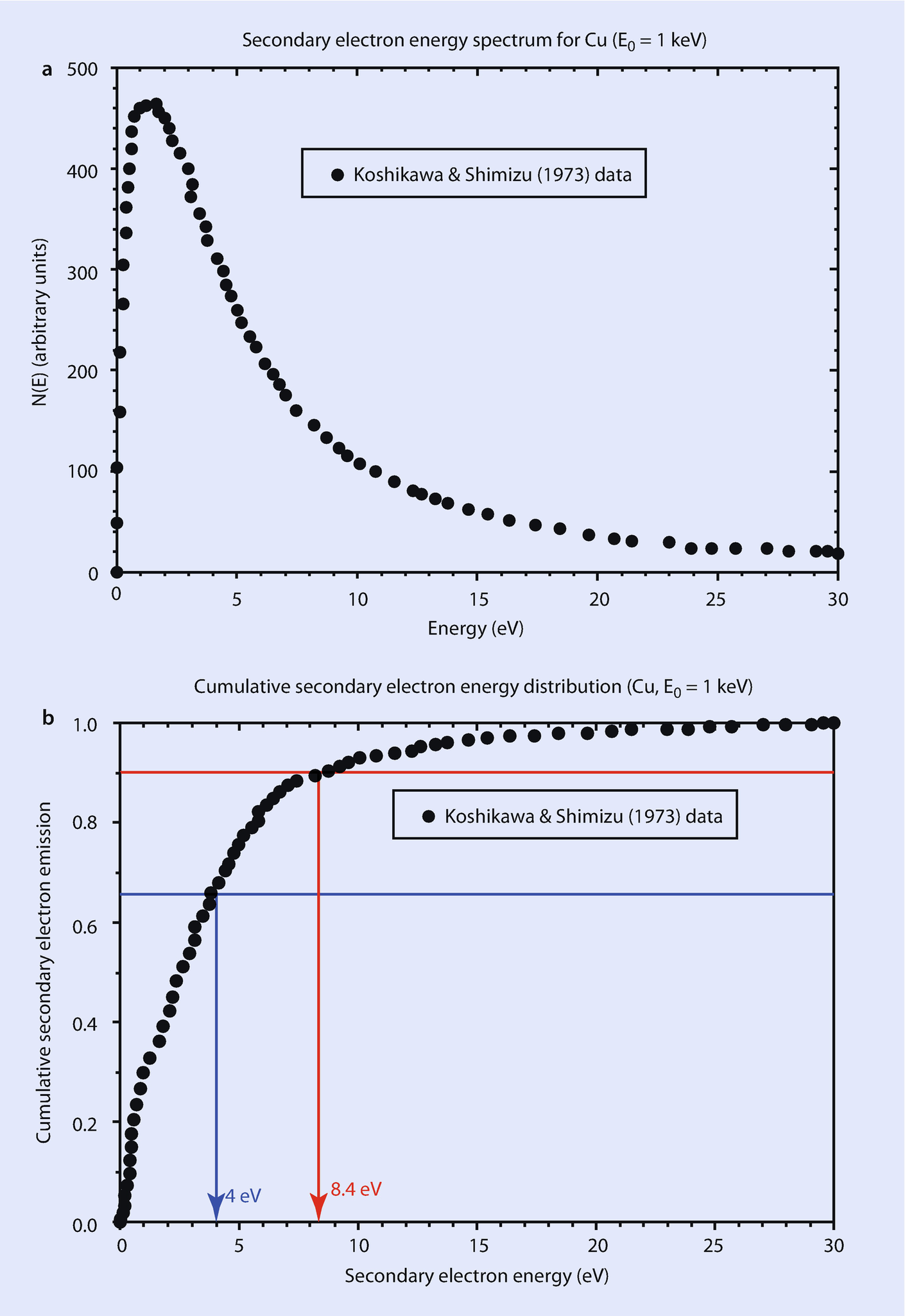
../images/271173_4_En_3_Chapter/271173_4_En_3_Fig1_HTML.png — Fig. 3.1
a Secondary electron energy spectrum for copper with an incident beam energy of E₀ = 1 keV (Koshikawa and Shimizu 1973). b (Data from ◘ Fig. 3.1a replotted as the cumulative energy distribution)

3.3 Escape Depth of Secondary Electrons

The kinetic energy of SE is so low that it has a strong influence on the depth from which SE can escape from the specimen. While some inelastic scattering processes are absent because of the low kinetic energy of SE, nevertheless SE suffer rapid energy loss with distance traveled, limiting the range of an SE to a few nanometers rather than the hundreds to thousands of nanometers for the energetic beam electrons and BSE. Thus, although SE are generated along the entire trajectory of a beam electron scattering in the target, only those SE generated close to a surface have a significant chance to escape. The probability of escape depends on the initial kinetic energy, the depth of generation, and the nature of the host material. Since there is a spectrum of initial kinetic energies, each energy represents a different escape probability and depth sensitivity. This complex behavior is difficult to measure directly, and instead researchers have made use of the Monte Carlo simulation to characterize the escape depth. ◘ Figure 3.2a shows the relative intensity of secondary electrons (over the energy range 0–50 eV) that escape from a copper target as a function of the depth of generation in the solid (Koshikawa and Shimizu 1974). ◘ Figure 3.2b shows this same data in the form of the cumulative secondary electron intensity as a function of initial generation depth. For copper, virtually no secondary electron escapes if it is created below approximately 8 nm from the surface, and 67 % of the secondary emission originates from a depth of less than 2.2 nm and 90 % from less than 4.4 nm. Kanaya and Ono (1984) modeled the mean secondary electron escape depth, d_esc, in terms of various material parameters:

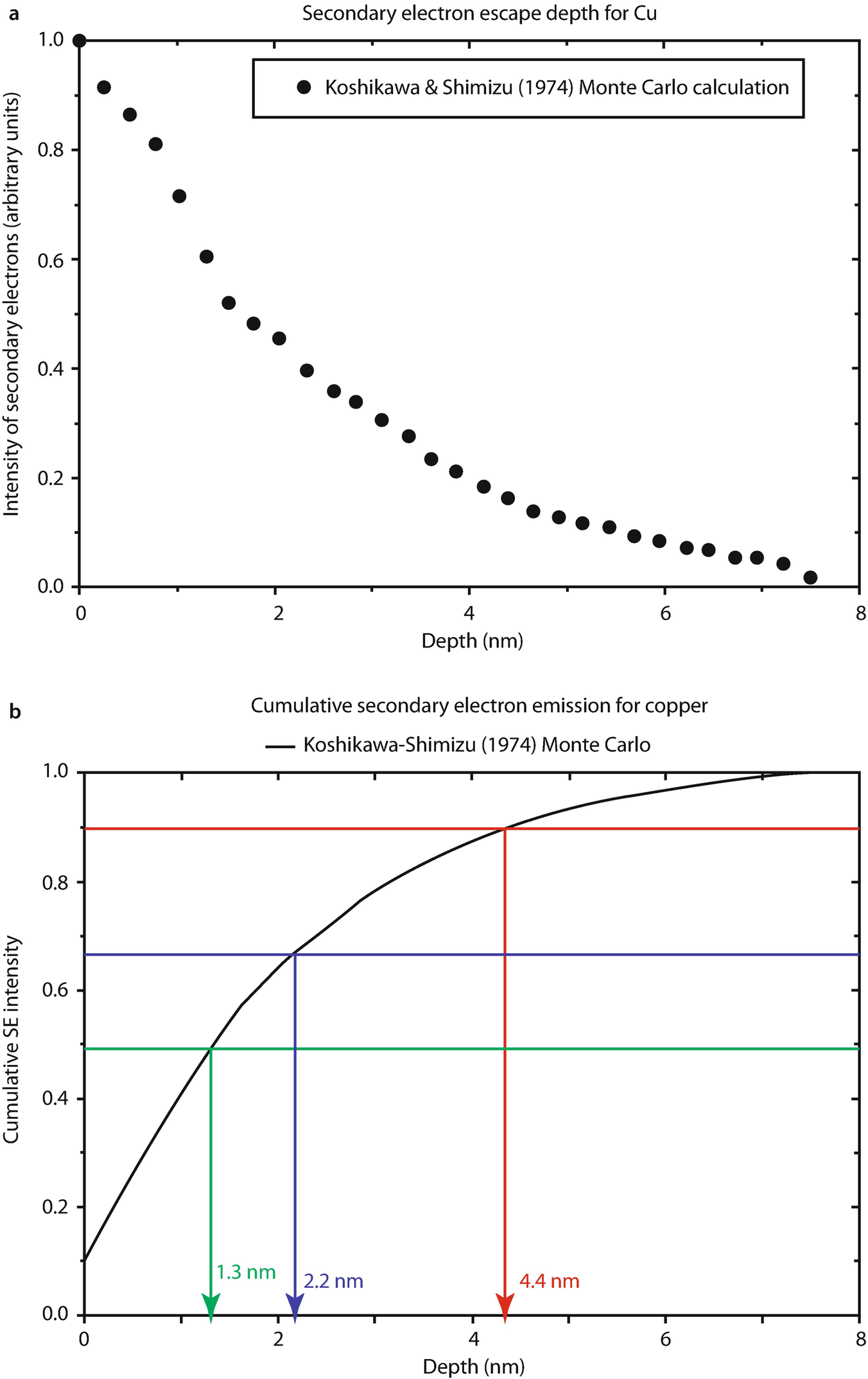
../images/271173_4_En_3_Chapter/271173_4_En_3_Fig2_HTML.png — Fig. 3.2
a Escape of secondary electrons from copper as a function of generation depth from Monte Carlo simulation (Koshikawa and Shimizu 1974). b (Data from ◘ Fig. 3.2a replotted to show the cumulative escape of secondary electrons as a function of depth of generation)

${d}_{esc}(nm)=0.267\ A\ I/\left(\rho {Z}^{0.66}\right)$

(3.2)

where A is the atomic weight (g/mol), ρ is the density (g/cm³), Z is the atomic number, and I is the first ionization potential (eV). When this model is applied to the solid elements of the Periodic Table, the complex behavior seen in ◘ Fig. 3.3 results. The mean escape depth varies from a low value of ~ 0.25 nm for Ce to a high value of 9 nm for Li. For copper, d_esc is calculated to be 1.8 nm, which can be compared to the 50 % escape value of 1.3 nm from the Monte Carlo simulation study in ◘ Fig. 3.2b. Systematic behavior of the atomic properties in Eq. 3.1 leads to systematic trends in the mean escape depth, with the low density alkali metals showing the largest values for the escape depth, while minima occur for the highest density elements in each period.

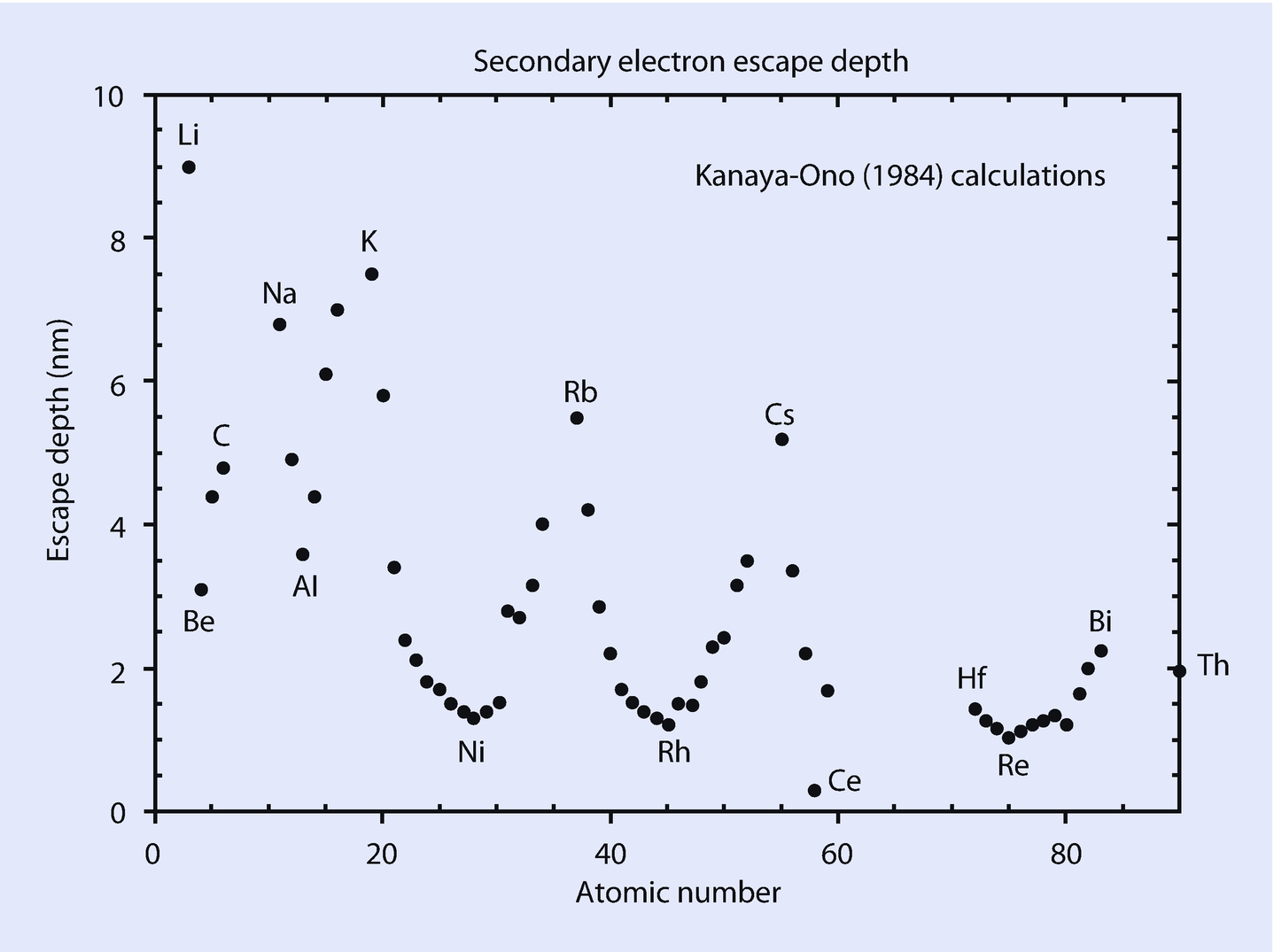
../images/271173_4_En_3_Chapter/271173_4_En_3_Fig3_HTML.png — Fig. 3.3
Mean secondary electron escape depth for various materials as modeled by Kanaya and Ono (1984)

3.4 Secondary Electron Yield Versus Atomic Number

◘ Figure 3.4 shows a plot of the secondary electron coefficient as a function of atomic number for an incident beam energy of E₀ = 5 keV with data taken from A Database of Electron-Solid Interactions of Joy (2012). The measurements of δ are chaotic and inconsistent. For example, the values of δ for gold reported by various workers range from approximately 0.4 to 1.2. Oddly, all of these measured values may be “correct” in the sense that a valid, reproducible measurement was made on the particular specimen used. This behavior is really an indication of how difficult it is to make a representative measurement of a property that results from very low energy electrons generated within and escaping from a very shallow layer below the surface. Thus, a surface modified by accumulations of oxide and contamination (e.g., adsorbed water, chemisorbed water, hydrocarbons, etc.) is likely to produce a value of δ that is different from the “ideal” pure element or pure compound value. If the specimen is pre-cleaned by ion bombardment in an ultrahigh vacuum electron beam instrument (chamber pressure maintained below 10⁻⁸ Pa) which preserves the clean surface, and if the surface composition is confirmed to be that of the pure element or compound by a surface-specific measurement method such as Auger electron spectroscopy or X-ray photoelectron spectroscopy, then the measured secondary electron coefficient is likely to be representative of the pure substance. However, the surfaces of most specimens examined in the conventional-vacuum SEM (chamber pressure ~ 10⁻⁴ Pa) or a variable pressure SEM (chamber pressure from 10⁻⁴ Pa to values as high as 2500 Pa) are not likely to be that of pure substances, but are almost inevitably covered with a complex mixture of oxides, hydrocarbons, and chemisorbed water molecules that quickly redeposit at such elevated pressures even when ion beam cleaning is utilized to expose the “true” surface. The effective secondary electron coefficient of a “real” material under typical SEM or VP-SEM vacuum conditions is unlikely to produce a consistent, predictable response as a function of the composition of the nominal substance under examination. Thus, while compositionally dependent secondary electron signals may be occasionally observed, they are generally not predictable and reproducible, which is the critical basis for establishing a useful contrast mechanism such as that found for backscattered electrons as a function of atomic number.

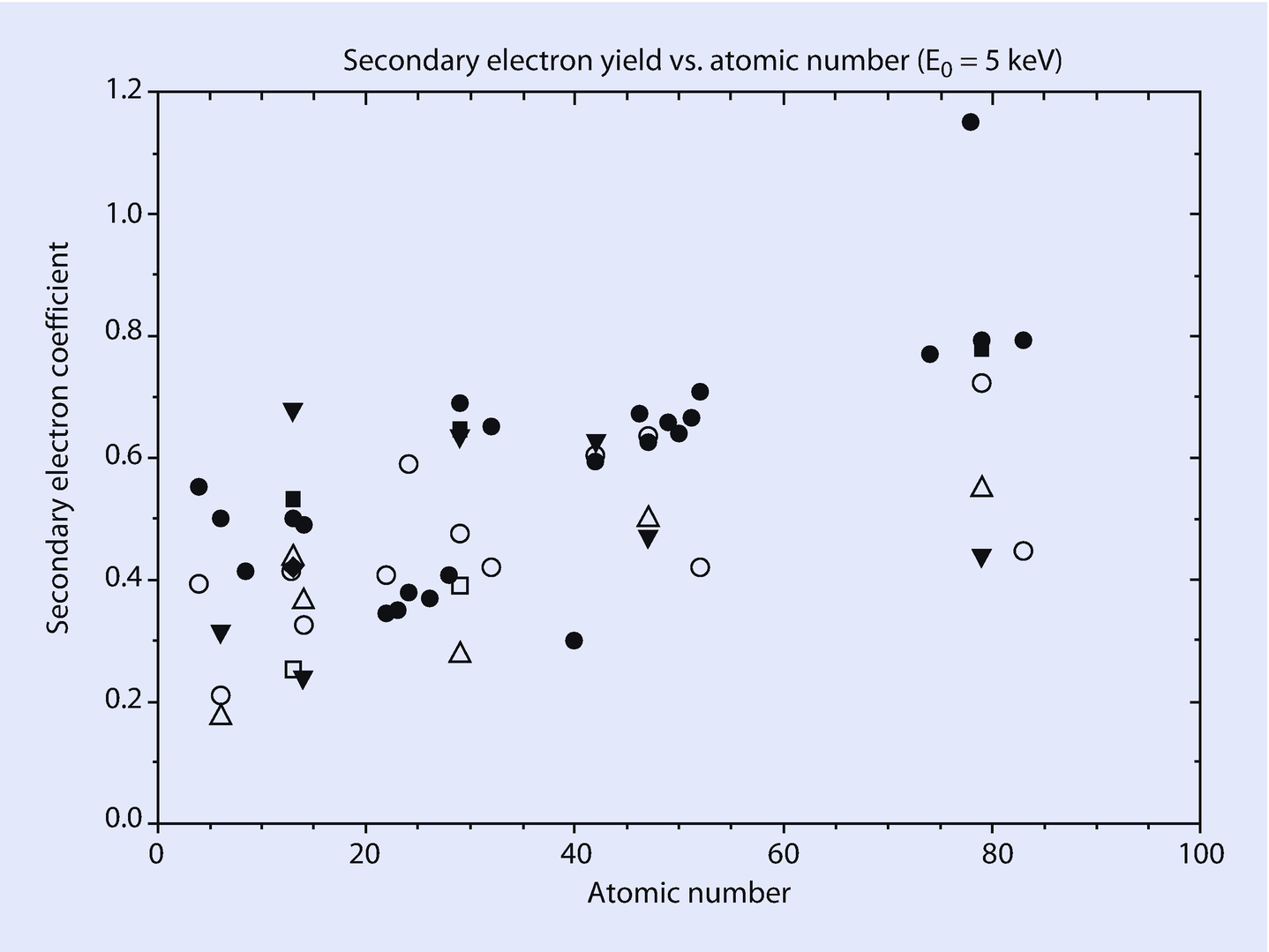
../images/271173_4_En_3_Chapter/271173_4_En_3_Fig4_HTML.png — Fig. 3.4
Secondary electron coefficient as a function of atomic number for E₀ = 5 keV (Data from the secondary electron database of Joy (2012))

3.5 Secondary Electron Yield Versus Specimen Tilt

When the secondary electron coefficient is measured as a function of the specimen tilt angle, θ (i.e., the specimen inclination to the beam, where a tilt of 0° means that the beam is perpendicular to the surface), a monotonic increase with tilt is observed, as shown for copper at two different incident beam energies in ◘ Fig. 3.5, which is taken from the measurements of Koshikawa and Shimizu (1973). This increase in δ with θ can be understood from the geometric argument presented schematically in ◘ Fig. 3.6. As the primary beam enters the specimen, the rate of secondary electron production is effectively constant along the path that lies within the shallow secondary electron escape depth because the beam electrons have not yet undergone sufficient scattering to modify their energies or trajectories. The length of the primary beam path within the depth of escape, d_esc, increases as the secant of the tilt angle. Assuming that the number of secondary electrons that eventually escape will be proportional to the number produced in this near surface region, the secondary electron coefficient is similarly expected to rise with the secant of the tilt angle. As shown in ◘ Fig. 3.5, the measured dependence of δ upon θ does not rise as fast as the secant relation that the simple geometric argument predicts. This deviation from the secant function model in ◘ Fig. 3.6 is due to the large contribution of secondary electrons produced by the exiting backscattered electrons which follow different trajectories through the escape layer, as discussed below.

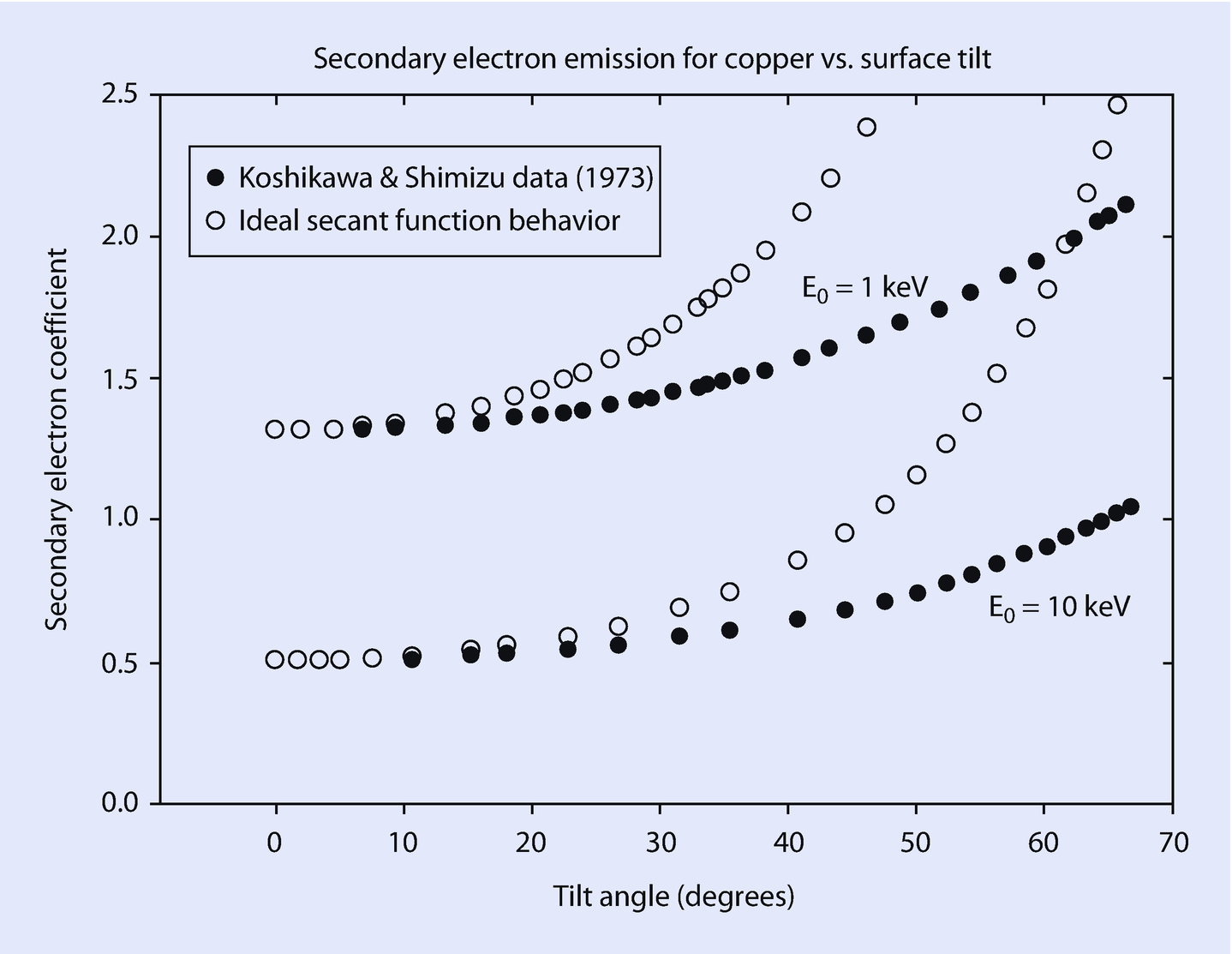
../images/271173_4_En_3_Chapter/271173_4_En_3_Fig5_HTML.png — Fig. 3.5
Behavior of the secondary electron coefficient as a function of surface tilt (Data of Koshikawa and Shimizu (1973)) showing a monotonic increase with tilt angle but at a much slower rate than would be predicted by a secant function

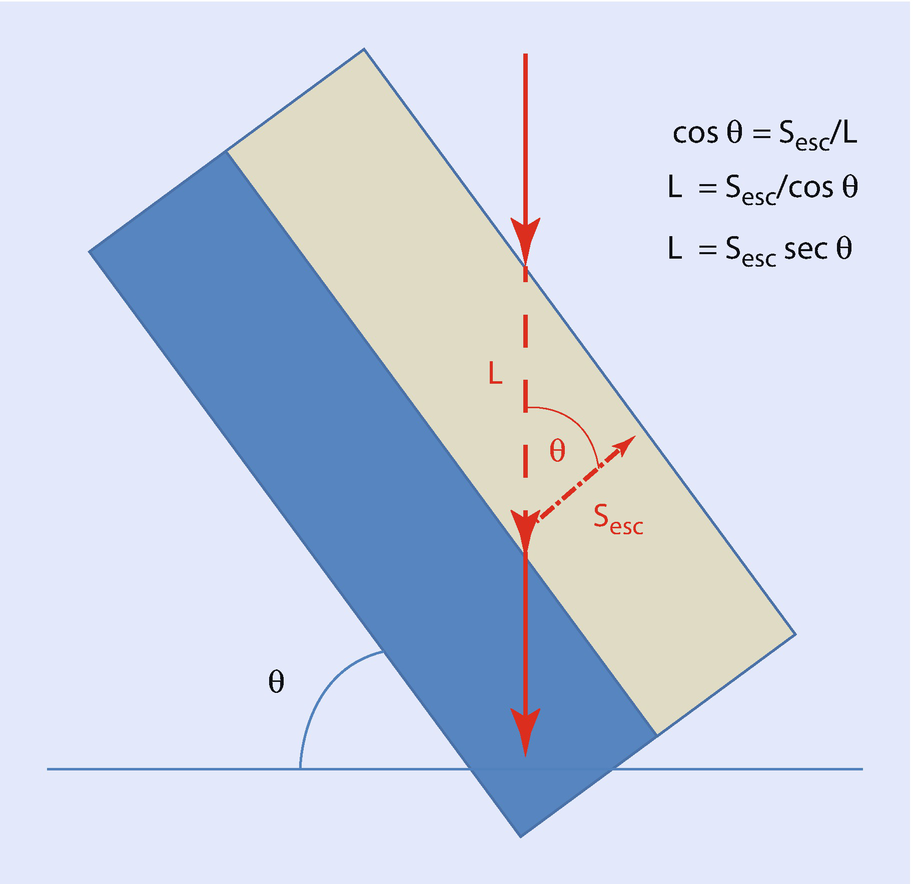
../images/271173_4_En_3_Chapter/271173_4_En_3_Fig6_HTML.png — Fig. 3.6
Simple geometric argument predicting that the secondary electron coefficient should follow a secant function of the tilt angle

The monotonic dependence of the secondary electron coefficient on the local surface inclination is an important factor in producing topographic contrast that reveals the shape of an object.

3.6 Angular Distribution of Secondary Electrons

When a secondary electron is generated within the escape depth below the surface, as shown in ◘ Fig. 3.7a, the shortest path to the surface, s, lies along the direction parallel to the local surface normal. For any other trajectory at an angle φ relative to this surface normal, the path length increases in length as s/cos φ. The probability of secondary electron escape decreases as the escape path length increases, so that the angular distribution of emitted secondary electrons is expected to follow a cosine relation with the emergence angle relative to the local surface normal. Behavior close to a cosine relation is seen in the Monte Carlo simulation of Koshikawa and Shimizu (1974) in ◘ Fig. 3.7b.

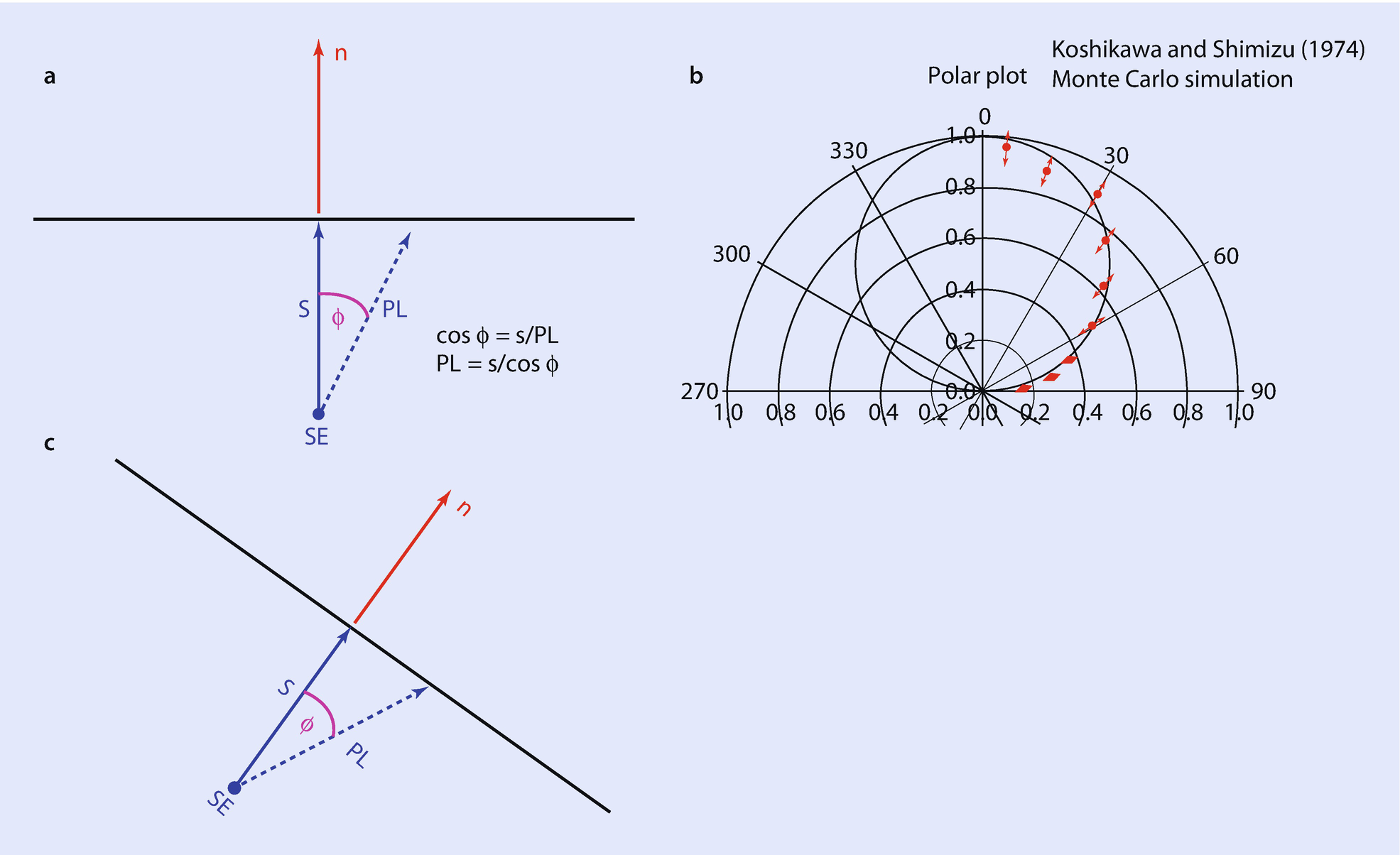
../images/271173_4_En_3_Chapter/271173_4_En_3_Fig7_HTML.png — Fig. 3.7
a Dependence of the secondary electron escape path length on the angle relative to the surface normal. The probability of escape decreases as this path length increases. b Angular distribution of secondary electrons as a function of the angle relative to the surface normal as simulated by Monte Carlo calculations (Koshikawa and Shimizu 1974) compared to a cosine function. c The escape path length situation of ◘ Fig. 3.7a for the case of a tilted specimen. A cosine dependence relative to the surface normal is again predicted

Even when the surface is highly tilted relative to the beam, the escape path length situation for a secondary electron generated below the surface is identical to the case for normal beam incidence, as shown in ◘ Fig. 3.7c. Thus, the secondary electron trajectories follow a cosine distribution relative to the local surface normal regardless of the specimen tilt.

3.7 Secondary Electron Yield Versus Beam Energy

The secondary electron coefficient increases as the incident beam energy decreases, as shown for copper in ◘ Fig. 3.8a for the conventional beam energy range (5 keV ≤ E₀ ≤ 30 keV) and in ◘ Fig. 3.8b for the low beam energy range (E₀ < 5 keV). This behavior arises from two principal factors: (1) as the beam electron energy decreases, the rate of energy loss, dE/ds, increases so that more energy is deposited per unit of beam electron path length leading to more secondary electron generation per unit of path length; and (2) the range of the beam electrons is reduced so more of that energy is deposited and more secondary electrons are generated in the near surface region from which secondary electrons can escape. This is a general behavior found across the Periodic Table, as seen in the plots for C, Al, Cu, Ag, and Au in ◘ Fig. 3.8c.

../images/271173_4_En_3_Chapter/271173_4_En_3_Fig8_HTML.png — Fig. 3.8
a Behavior of the secondary electron coefficient as a function of incident beam energy for the conventional beam energy range, E₀ = 5–30 keV (Data of Moncrieff and Barker (1976)). b Behavior of the secondary electron coefficient as a function of incident beam energy for the low beam energy range, E₀ < 5 keV (data) (Data of Bongeler et al. (1993)). c Dependence of the secondary electron coefficient on incident beam energy for C, Al, Cu, Ag, and Au (Reimer and Tolkamp 1980)

3.8 Spatial Characteristics of Secondary Electrons

As the beam electrons enter the sample surface, they begin to generate secondary electrons in a cylindrical volume whose cross section is defined by the footprint of the beam on the entrance surface and whose height is the escape depth of the SE, as shown schematically in ◘ Fig. 3.9 These entrance surface SE, designated the SE₁ class, preserve the lateral spatial resolution information defined by the dimensions of the focused beam and are similarly sensitive to the properties of the near surface region due to the shallow scale of their origin. As the beam electrons move deeper into the solid, they continue to generate SE, but these SE rapidly lose their small initial kinetic energy and are completely reabsorbed within an extremely short range. However, for those beam electrons that subsequently undergo enough scattering to return to the entrance surface to emerge as backscattered electrons (or reach any other surface for specimens with more complex topography than a simple flat bulk target), the SE that they continue to generate as they approach the surface region will escape and add to the total secondary electron production, as shown in ◘ Fig. 3.9. This class of SE is designated SE₂ and they are indistinguishable from the SE₁ class based on their energy and angular distributions. However, because of their origin from the backscattered electrons, the SE₂ class actually carries the degraded lateral spatial distribution of the BSE: because the relative number of SE₂ rises and falls with backscattering, the SE₂ signal actually carries the same information as BSE. That is, the relative number of the SE₂ scales with whatever specimen property affects electron backscattering. Finally, the BSE that leave the specimen are energetic, and after traveling millimeters to centimeters in the specimen chamber, these BSE are likely to hit other metal surfaces (objective lens polepiece, chamber walls, stage components, etc.), generating a third set of secondary electrons designated SE₃. The SE₃ class again represents BSE information, including the degraded spatial resolution, not true SE₁ information and resolution. The SE₁ and SE₂ classes represent an inherent property of a material, while the SE₃ class depends on the details of the SEM specimen chamber. Peters (1984) measured the three secondary electron classes for thin and thick gold targets to estimate the relative populations of each class:

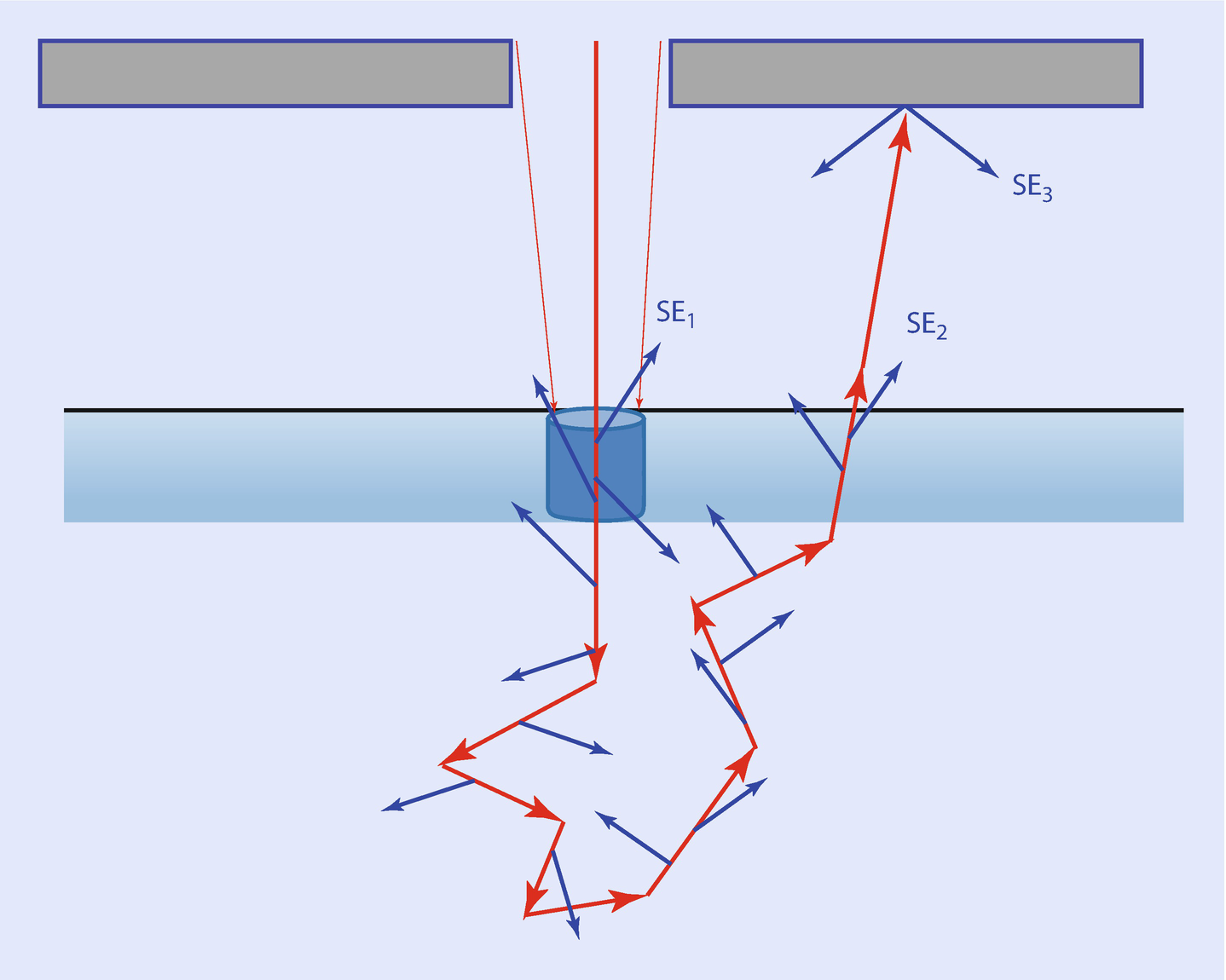
../images/271173_4_En_3_Chapter/271173_4_En_3_Fig9_HTML.png — Fig. 3.9
Schematic diagram showing the origins of the SE₁, SE₂, and SE₃ classes of secondary electrons. The SE₁ class carries the lateral and near-surface spatial information defined by the incident beam, while the SE₂ and SE₃ classes actually carry backscattered electron information. The blue rectangle represents the escape depth for SE, and the cylinder represents the volume from which the SE₁ escape

Incident beam footprint, high resolution, SE₁ (9 %)
BSE generated at specimen, low resolution, SE₂ (28 %)
BSE generated remotely on lens, chamber walls, SE₃ (61 %)

A small SE contribution designated the SE₄ class arises from pre-specimen instrumental sources such as the final aperture (2 %) that depends in detail on the instrument construction (apertures, magnetic fields, etc.). These measurements show that for gold the sum of the SE₂ and SE₃ classes which actually carry BSE is nearly ten times larger than the high resolution, high surface sensitivity SE₁ component. These three classes of secondary electrons influence SEM images of compositional structures and topographic structures in complex ways. The appearance of the SE image of a structure depends on the details of the secondary electron emission and the properties of the secondary electron detector used to capture the signal, as discussed in detail in the image formation module.

Open Access This chapter is licensed under the terms of the Creative Commons Attribution-NonCommercial 2.5 International License (http://creativecommons.org/licenses/by-nc/2.5/), which permits any noncommercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

References

Bongeler R, Golla U, Kussens M, Reimer L, Schendler B, Senkel R, Spranck M (1993) Electron-specimen interactions in low voltage scanning electron microscopy. Scanning 15:1Crossref
Joy D (2012) Can be found in chapter 3 on SpringerLink: http://link.springer.com/chapter/10.1007/978-1-4939-6676-9_3
Kanaya K, Ono S (1984) Interaction of electron beam with the target in scanning electron microscope. In: Kyser DF, Niedrig H, Newbury DE, Shimizu R (eds) Electron interactions with solids. SEM, Inc, Chicago, pp 69–98
Koshikawa T, Shimizu R (1973) Secondary electron and backscattering measurements for polycrystalline copper with a retarding-field analyser. J Phys D Appl Phys 6:1369Crossref
Koshikawa T, Shimizu R (1974) A Monte Carlo calculation of low-energy secondary electron emission from metals. J Phys D Appl Phys 7:1303Crossref
Peters K-R (1984) Generation, collection and properties of an SE-I enriched signal suitable for high resolution SEM on bulk specimens. In: Kyser DF, Niedrig H, Newbury DE, Shimizu R (eds) Electron beam interactions with solids. SEM, Inc, AMF O’Hare, p 363
Moncrieff DA, Barker PR (1976) Secondary electron emission in the scanning electron microscope. Scanning 1:195Crossref
Reimer L, Tolkamp C (1980) Measuring the backscattering coefficient and secondary electron yield inside a scanning electron microscope. Scanning 3:35Crossref