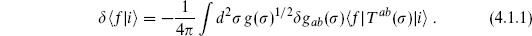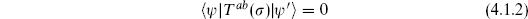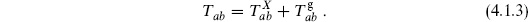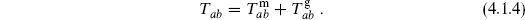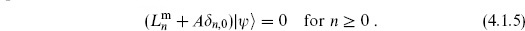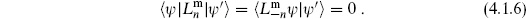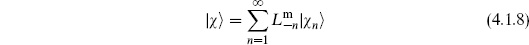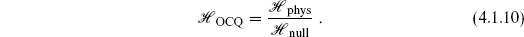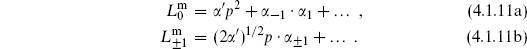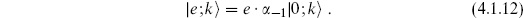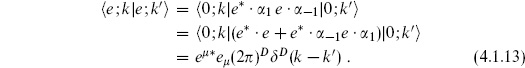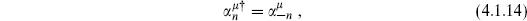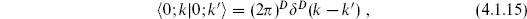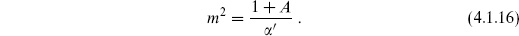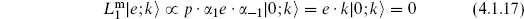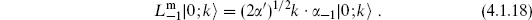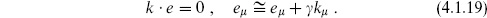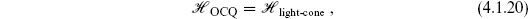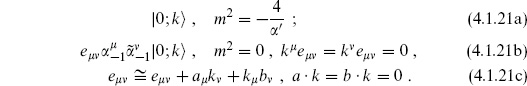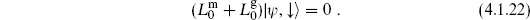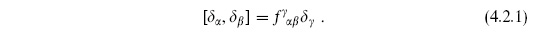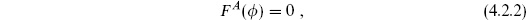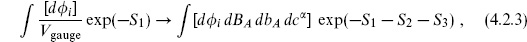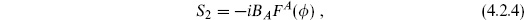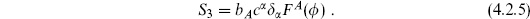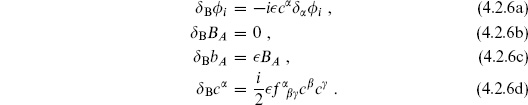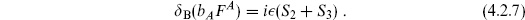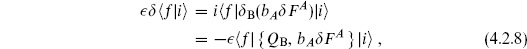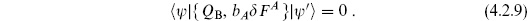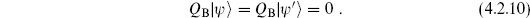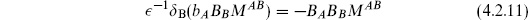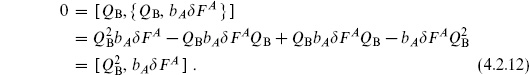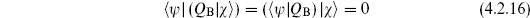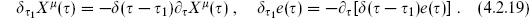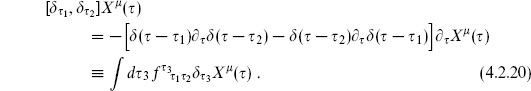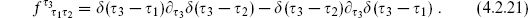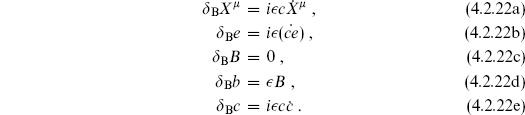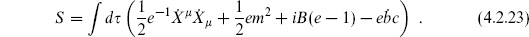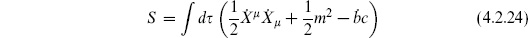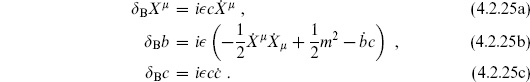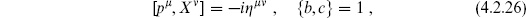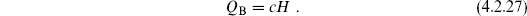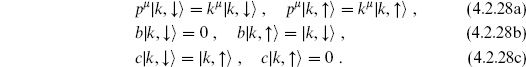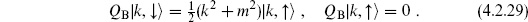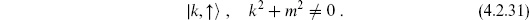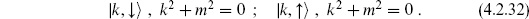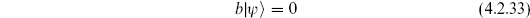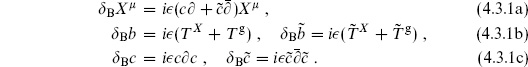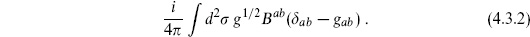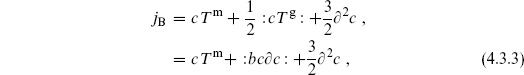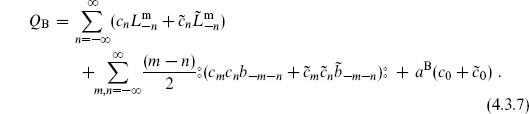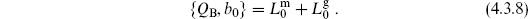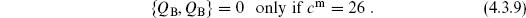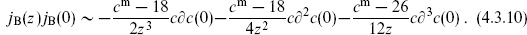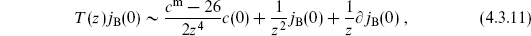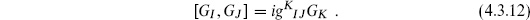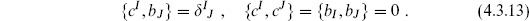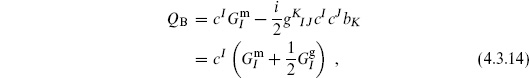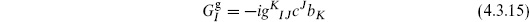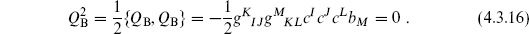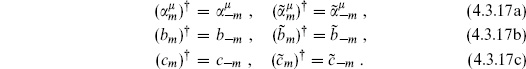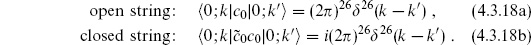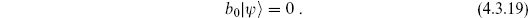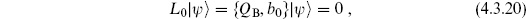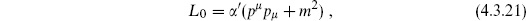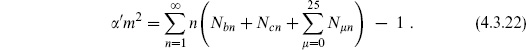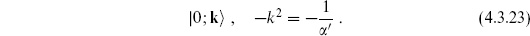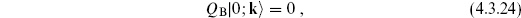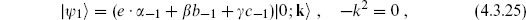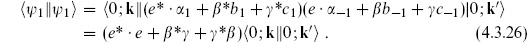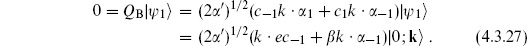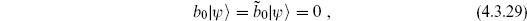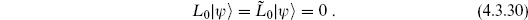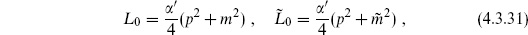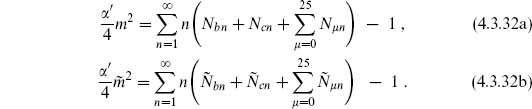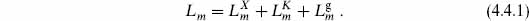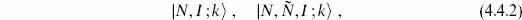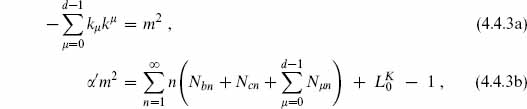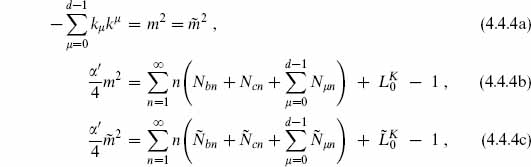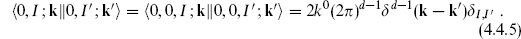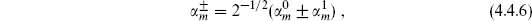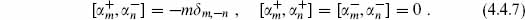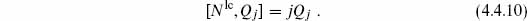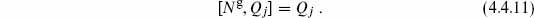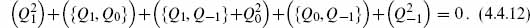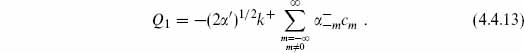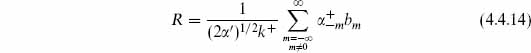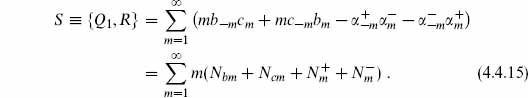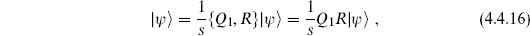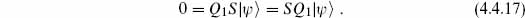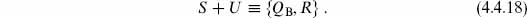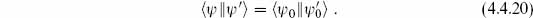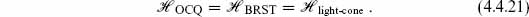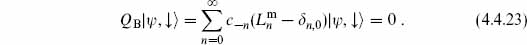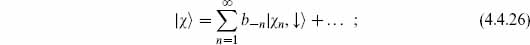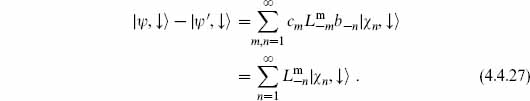4
The string spectrum
4.1 Old covariant quantization
In conformal gauge, the world-sheet fields are X and the Faddeev–Popov ghosts bab and ca. The Hilbert space is bigger than the actual physical spectrum of the string: the D sets of
and the Faddeev–Popov ghosts bab and ca. The Hilbert space is bigger than the actual physical spectrum of the string: the D sets of 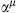 oscillators include unphysical oscillations of the coordinate system, and there are ghost oscillators. As is generally the case in covariant gauges, there are negative norm states from the timelike oscillators (because the commutator is proportional to the spacetime metric
oscillators include unphysical oscillations of the coordinate system, and there are ghost oscillators. As is generally the case in covariant gauges, there are negative norm states from the timelike oscillators (because the commutator is proportional to the spacetime metric 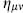 ), and also from the ghosts.
), and also from the ghosts.
The actual physical space is smaller. To see how to identify this smaller space, consider the amplitude on the infinite cylinder for some initial state |i  to propagate to some final state |f
to propagate to some final state |f  . Suppose that we have initially used the local symmetries to fix the metric to a form gab(
. Suppose that we have initially used the local symmetries to fix the metric to a form gab( ). Consider now a different gauge, with metric gab(
). Consider now a different gauge, with metric gab( ) +
) +  gab(
gab( ). A physical amplitude should not depend on this choice. Of course, for a change in the metric we know how the path integral changes. From the definition (3.4.4) of Tab,
). A physical amplitude should not depend on this choice. Of course, for a change in the metric we know how the path integral changes. From the definition (3.4.4) of Tab,
In order that the variation vanish for arbitrary changes in the metric, we need
for arbitrary physical states 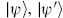 .
.
There is another way to think about this. The original equation of motion from variation of gab was Tab = 0. After gauge-fixing, this does not hold as an operator equation: we have a missing equation of motion because we do not vary gab in the gauge-fixed theory. The condition (4.1.2) says that the missing equation of motion must hold for matrix elements between physical states. When we vary the gauge we must take into account the change in the Faddeev–Popov determinant, so the energy-momentum tensor in the matrix element is the sum of the X and ghost contributions,
and ghost contributions,
The X may be replaced by a more general CFT (which we will refer to as the matter CFT), in which case
may be replaced by a more general CFT (which we will refer to as the matter CFT), in which case
In the remainder of this section we will impose the condition (4.1.2) in a simple but somewhat ad hoc way. This is known as the old covariant quantization (OCQ), and it is sufficient for many purposes. In the next section we will take a more systematic approach, BRST quantization. These are in fact equivalent, as will be shown in section 4.4.
In the ad hoc approach, we will simply ignore the ghosts and try to restrict the matter Hilbert space so that the missing equation of motion 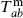 = 0 holds for matrix elements. In terms of the Laurent coefficients this is
= 0 holds for matrix elements. In terms of the Laurent coefficients this is 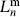 = 0, and in the closed string also
= 0, and in the closed string also 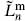 = 0. One might first try to require physical states to satisfy
= 0. One might first try to require physical states to satisfy 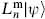 = 0 for all n, but this is too strong; acting on this equation with
= 0 for all n, but this is too strong; acting on this equation with  and forming the commutator, one encounters an inconsistency due to the central charge in the Virasoro algebra. However, it is sufficient that only the Virasoro lowering and zero operator annihilate physical states,
and forming the commutator, one encounters an inconsistency due to the central charge in the Virasoro algebra. However, it is sufficient that only the Virasoro lowering and zero operator annihilate physical states,
For n < 0 we then have
We have used
as follows from the Hermiticity of the energy-momentum tensor. The conditions (4.1.5) are consistent with the Virasoro algebra. At n = 0 we have as usual included the possibility of an ordering constant. A state satisfying (4.1.5) is called physical. In the terminology of eq. (2.9.8), a physical state is a highest weight state of weight –A. The condition (4.1.5) is similar to the Gupta–Bleuler quantization of electrodynamics.
Using the adjoint (4.1.7), one sees that a state of the form
is orthogonal to all physical states for any 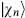 . Such a state is called spurious. A state that is both physical and spurious is called null. If
. Such a state is called spurious. A state that is both physical and spurious is called null. If 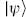 is physical and
is physical and 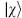 is null, then
is null, then 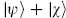 is also physical and its inner product with any physical state is the same as that of
is also physical and its inner product with any physical state is the same as that of 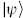 . Therefore these two states are physically indistinguishable, and we identify
. Therefore these two states are physically indistinguishable, and we identify
The real physical Hilbert space is then the set of equivalence classes,
Let us see how this works for the first two levels of the open string in flat spacetime, not necessarily assuming D = 26. The only relevant terms are
At the lowest mass level, the only state is |0;k  . The only nontrivial condition at this level is
. The only nontrivial condition at this level is 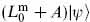 = 0, giving m2 = A/
= 0, giving m2 = A/ ′. There are no null states at this level — the Virasoro generators in the spurious state (4.1.8) all contain raising operators. Thus there is one equivalence class, corresponding to a scalar particle.
′. There are no null states at this level — the Virasoro generators in the spurious state (4.1.8) all contain raising operators. Thus there is one equivalence class, corresponding to a scalar particle.
At the next level there are D states
The norm is
We have used
as follows from the Hermiticity of X , and also
, and also
as follows from momentum conservation. The timelike excitation has a negative norm.
The 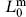 condition gives
condition gives
The other nontrivial physical state condition is
and so k · e = 0. There is a spurious state at this level:
That is, 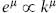 is spurious. There are now three cases:
is spurious. There are now three cases:
(i) If A > –1, the mass-squared is positive. Going to the rest frame, the physical state condition removes the negative norm timelike polarization. The spurious state (4.1.18) is not physical, k · k 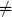 0, so there are no null states and the spectrum consists of the D − 1 positive-norm states of a massive vector particle.
0, so there are no null states and the spectrum consists of the D − 1 positive-norm states of a massive vector particle.
(ii) If A = −1, the mass-squared is zero. Now k · k = 0 so the spurious state is physical and null. Thus,
This describes the D − 2 positive-norm states of a massless vector particle.
(iii) If A < −1, the mass-squared is negative. The momentum is spacelike, so the physical state condition removes a positive-norm spacelike polarization. The spurious state is not physical, so we are left with a tachyonic vector particle with D − 2 positive-norm states and one negative-norm state.
Case (iii) is unacceptable. Case (ii) is the same as the light-cone quantization. Case (i) is not the same as the light-cone spectrum, having different masses and an extra state at the first level, but does not have any obvious inconsistency. The difficulty is that there is no known way to give such a theory consistent interactions. Case (ii) is the one of interest in string theory, and the one we will recover from the more general approach of the next section.
The result at the next level is quite interesting: it depends on the constant A and also on the spacetime dimension D. Restricting to the value A = −1 found at the first excited level, the spectrum only agrees with the light-cone spectrum if in addition D = 26. If D > 26, there are negative-norm states; if D < 26 the OCQ spectrum has positive norm but more states than in light-cone quantization. The derivation is left to the reader. The OCQ at A = −1 and D = 26 is in fact the same as light-cone quantization at all mass levels,
as will be shown in section 4.4. It is only in this case that consistent interactions are known.
The extension to the closed string is straightforward. There are two sets of oscillators and two sets of Virasoro generators, so at each level the spectrum is the product of two copies of the open string spectrum (except for the normalization of p2 in 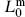 ). The first two levels are then
). The first two levels are then
The relevant values are again A = −1, D = 26. As in light-cone quantization, there are (D – 2)2 massless states forming a traceless symmetric tensor, an antisymmetric tensor, and a scalar.
Mnemonic
For more general string theories, it is useful to have a quick mnemonic for obtaining the zero-point constant. As will be derived in the following sections, the 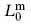 condition can be understood as
condition can be understood as
That is, one includes the ghost contribution with the ghosts in their ground state |↓ , which has
, which has 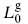 = −1. The L0 generators differ from the Hamiltonian by a shift (2.6.10) proportional to the central charge, but the total central charge is zero in string theory so we can just as well write this condition as
= −1. The L0 generators differ from the Hamiltonian by a shift (2.6.10) proportional to the central charge, but the total central charge is zero in string theory so we can just as well write this condition as
Now apply the mnemonic for zero-point energies given at the end of chapter 2. In particular, the ghosts always cancel the 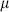 = 0, 1 oscillators because they have the same periodicities but opposite statistics. So the rule is that A is given as the sum of the zero-point energies of the transverse oscillators. This is the same rule as in the light-cone, giving here
= 0, 1 oscillators because they have the same periodicities but opposite statistics. So the rule is that A is given as the sum of the zero-point energies of the transverse oscillators. This is the same rule as in the light-cone, giving here 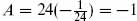 .
.
Incidentally, for the purposes of counting the physical states (but not for their precise form) one can simply ignore the ghost and 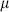 = 0, 1 oscillators and count transverse excitations as in the light-cone.
= 0, 1 oscillators and count transverse excitations as in the light-cone.
The condition (4.1.22) requires the weight of the matter state to be 1. Since the physical state condition requires the matter state to be a highest weight state, the vertex operator must then be a weight 1 or (1,1) tensor. This agrees with the condition from section 3.6 that the integrated vertex operator be conformally invariant, which gives another understanding of the condition A = −1.
4.2 BRST quantization
We now return to a more systematic study of the spectrum. The condition (4.1.2) is not sufficient to guarantee gauge invariance. It implies invariance for arbitrary fixed choices of gab, but this is not the most general gauge. In light-cone gauge, for example, we placed some conditions on X and some conditions on gab. To consider the most general possible variation of the gauge condition, we must allow
and some conditions on gab. To consider the most general possible variation of the gauge condition, we must allow  gab to be an operator, that is, to depend on the fields in the path integral.
gab to be an operator, that is, to depend on the fields in the path integral.
In order to derive the full invariance condition, it is useful to take a more general and abstract point of view. Consider a path integral with a local symmetry. The path integral fields are denoted 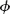 i, which in the present case would be X
i, which in the present case would be X (
( ) and gab(
) and gab( ). Here we use a very condensed notation, where i labels the field and also represents the coordinate
). Here we use a very condensed notation, where i labels the field and also represents the coordinate  . The gauge invariance is
. The gauge invariance is 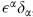 , where again
, where again  includes the coordinate. By assumption the gauge parameters
includes the coordinate. By assumption the gauge parameters 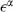 are real, since we can always separate a complex parameter into its real and imaginary parts. The gauge transformations satisfy an algebra
are real, since we can always separate a complex parameter into its real and imaginary parts. The gauge transformations satisfy an algebra
Now fix the gauge by conditions
where once again A includes the coordinate. Following the same Faddeev–Popov procedure as in section 3.3, the path integral becomes
where S1 is the original gauge-invariant action, S2 is the gauge-fixing action
and S3 is the Faddeev–Popov action
We have introduced the field BA to produce an integral representation of the gauge-fixing  (FA).
(FA).
There are two things to notice about this action. The first is that it is invariant under the Becchi–Rouet–Stora–Tyutin (BRST) transformation
This transformation mixes commuting and anticommuting objects, so that  must be taken to be anticommuting. There is a conserved ghost number, which is + 1 for c
must be taken to be anticommuting. There is a conserved ghost number, which is + 1 for c , −1 for bA and
, −1 for bA and  , and 0 for all other fields. The original action S1 is invariant by itself, because the action of
, and 0 for all other fields. The original action S1 is invariant by itself, because the action of  B on
B on 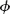 i is just a gauge transformation with parameter
i is just a gauge transformation with parameter 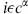 . The variation of S2 cancels the variation of bA in S3, while the variations of
. The variation of S2 cancels the variation of bA in S3, while the variations of 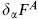 and c
and c in S3 cancel.
in S3 cancel.
The second key property is that
Now consider a small change  F in the gauge-fixing condition. The change in the gauge-fixing and ghost actions gives
F in the gauge-fixing condition. The change in the gauge-fixing and ghost actions gives
where we have written the BRST variation as an anticommutator with the corresponding conserved charge QB.
Therefore, physical states must satisfy
In order for this to hold for arbitrary  F, it must be that
F, it must be that
This is the essential condition: physical states must be BRST-invariant. We have assumed that 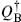 = QB. There are several ways to see that this must indeed be the case. One is that if
= QB. There are several ways to see that this must indeed be the case. One is that if 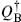 were different, it would have to be some other symmetry, and there is no candidate. A better argument is that the fields c
were different, it would have to be some other symmetry, and there is no candidate. A better argument is that the fields c and bA are like anticommuting versions of the gauge parameter
and bA are like anticommuting versions of the gauge parameter 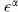 and Lagrange multiplier BA, and so inherit their reality properties.
and Lagrange multiplier BA, and so inherit their reality properties.
As an aside, we may also add to the action a term proportional to
for any constant matrix MAB. By the above argument, amplitudes between physical states are unaffected. The integral over BA now produces a Gaussian rather than a delta function: these are the Gaussian-averaged gauges, which include for example the covariant  -gauges of gauge theory.
-gauges of gauge theory.
There is one more key idea. In order to move around in the space of gauge choices, the BRST charge must remain conserved. Thus it must commute with the change in the Hamiltonian,
In order for this to vanish for general changes of gauge, we need
That is, the BRST charge is nilpotent; the possibility 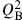 = constant is excluded because
= constant is excluded because 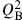 has ghost number 2. The reader can check that acting twice with the BRST transformation (4.2.6) leaves all fields invariant. In particular,
has ghost number 2. The reader can check that acting twice with the BRST transformation (4.2.6) leaves all fields invariant. In particular,
The product of ghosts is antisymmetric on the indices 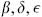 , and the product of structure functions then vanishes by the Jacobi identity.
, and the product of structure functions then vanishes by the Jacobi identity.
We should mention that we have made two simplifying assumptions about the gauge algebra (4.2.1). The first is that the structure constants 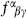 are constants, independent of the fields, and the second is that the algebra does not have, on the right-hand side, additional terms proportional to the equations of motion. More generally, both of these assumptions break down. In these cases, the BRST formalism as we have described it does not give a nilpotent transformation, and a generalization, the Batalin–Vilkovisky (BV) formalism, is needed. The BV formalism has had various applications in string theory, but we will not have a need for it.
are constants, independent of the fields, and the second is that the algebra does not have, on the right-hand side, additional terms proportional to the equations of motion. More generally, both of these assumptions break down. In these cases, the BRST formalism as we have described it does not give a nilpotent transformation, and a generalization, the Batalin–Vilkovisky (BV) formalism, is needed. The BV formalism has had various applications in string theory, but we will not have a need for it.
The nilpotence of QB has an important consequence. A state of the form
will be annihilated by QB for any 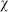 and so is physical. However, it is orthogonal to all physical states including itself:
and so is physical. However, it is orthogonal to all physical states including itself:
if 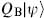 = 0. All physical amplitudes involving such a null state thus vanish. Two physical states that differ by a null state,
= 0. All physical amplitudes involving such a null state thus vanish. Two physical states that differ by a null state,
will have the same inner products with all physical states and are therefore physically equivalent. So, just as for the OCQ, we identify the true physical space with a set of equivalence classes, states differing by a null state being equivalent. This is a natural construction for a nilpotent operator, and is known as the cohomology of QB. Other examples of nilpotent operators are the exterior derivative in differential geometry and the boundary operator in topology. In cohomology, the term closed is often used for states annihilated by QB and the term exact for states of the form (4.2.15). Thus, our prescription is
We will see explicitly in the remainder of the chapter that this space has the expected form in string theory. Essentially, the invariance condition removes one set of unphysical X oscillators and one set of ghost oscillators, and the equivalence relation removes the other set of unphysical X
oscillators and one set of ghost oscillators, and the equivalence relation removes the other set of unphysical X oscillators and the other set of ghost oscillators.
oscillators and the other set of ghost oscillators.
Point-particle example
Let us consider an example, the point particle. Expanding out the condensed notation above, the local symmetry is coordinate reparameterization 
 (
( ), so the index
), so the index  just becomes
just becomes  and a basis of infinitesimal transformations is
and a basis of infinitesimal transformations is 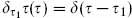 . These act on the fields as
. These act on the fields as
Acting with a second transformation and forming the commutator, we have
From the commutator we have determined the structure function
The BRST transformation is then
The gauge e( ) = 1 is analogous to the unit gauge for the string, using the single coordinate freedom to fix the single component of the tetrad, so F(
) = 1 is analogous to the unit gauge for the string, using the single coordinate freedom to fix the single component of the tetrad, so F( ) = 1 −e(
) = 1 −e( ). The gauge-fixed action is then
). The gauge-fixed action is then
We will find it convenient to integrate B out, thus fixing e = 1. This leaves only the fields X , b, and c, with action
, b, and c, with action
Since B is no longer present, we have used the equation of motion from e to replace B in the transformation law for b. The reader can check that the new transformation (4.2.25) is a symmetry of the action and is nilpotent. This always works when the fields BA are integrated out, though 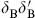 b is no longer identically zero but is proportional to the equations of motion. This is perfectly satisfactory:
b is no longer identically zero but is proportional to the equations of motion. This is perfectly satisfactory: 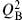 = 0 holds as an operator equation, which is what we need.
= 0 holds as an operator equation, which is what we need.
The canonical commutators are
with 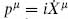 , the i being from the Euclidean signature. The Hamiltonian is
, the i being from the Euclidean signature. The Hamiltonian is 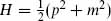 , and the Noether procedure gives the BRST operator
, and the Noether procedure gives the BRST operator
The structure here is analogous to what we will find for the string. The constraint (the missing equation of motion) is H = 0, and the BRST operator is c times this.
The ghosts generate a two-state system, so a complete set of states is  , where
, where
The action of the BRST operator on these is
From this it follows that the closed states are
and that the exact states are
The closed states that are not exact are
That is, physical states must satisfy the mass-shell condition, but we have two copies of the expected spectrum. In fact, only states |k,↓ satisfying the additional condition
satisfying the additional condition
appear in physical amplitudes. The origin of this additional condition is kinematic. For k2+m2 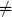 0, the states |k, ↑
0, the states |k, ↑ are exact — they are orthogonal to all physical states and their amplitudes must vanish identically. So the amplitudes can only be proportional to
are exact — they are orthogonal to all physical states and their amplitudes must vanish identically. So the amplitudes can only be proportional to  (k2 + m2). But amplitudes in field theory and in string theory, while they may have poles and cuts, never have delta functions (except in D = 2 where the kinematics is special). So they must vanish identically.
(k2 + m2). But amplitudes in field theory and in string theory, while they may have poles and cuts, never have delta functions (except in D = 2 where the kinematics is special). So they must vanish identically.
4.3 BRST quantization of the string
In string theory, the BRST transformation is
The reader can derive this following the point-particle example. To the sum of the Polyakov and ghost actions, add the gauge-fixing term
The transformation  Bbab =
Bbab =  Bab becomes (4.3.1) after integrating over Bab and using the gab equation of motion to replace Bab in the transformation. The Weyl ghost is just a Lagrange multiplier, making bab traceless. Again, the reader can check nilpotence up to the equations of motion. The similarity between the string BRST transformation (4.3.1) and the particle case (4.2.25) is evident. Replacing the X
Bab becomes (4.3.1) after integrating over Bab and using the gab equation of motion to replace Bab in the transformation. The Weyl ghost is just a Lagrange multiplier, making bab traceless. Again, the reader can check nilpotence up to the equations of motion. The similarity between the string BRST transformation (4.3.1) and the particle case (4.2.25) is evident. Replacing the X with a general matter CFT, the BRST transformation of the matter fields is a conformal transformation with
with a general matter CFT, the BRST transformation of the matter fields is a conformal transformation with  (z) = c(z), while Tm replaces TX in the transformation of b.
(z) = c(z), while Tm replaces TX in the transformation of b.
Noether’s theorem gives the BRST current
and correspondingly for 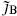 . The final term in the current is a total derivative and does not contribute to the BRST charge; it has been added by hand to make the BRST current a tensor. The OPEs of the BRST current with the ghost fields and with a general matter tensor field are
. The final term in the current is a total derivative and does not contribute to the BRST charge; it has been added by hand to make the BRST current a tensor. The OPEs of the BRST current with the ghost fields and with a general matter tensor field are
The simple poles reflect the BRST transformations (4.3.1) of these fields.
The BRST operator is
By the usual contour argument, the OPE implies
In terms of the ghost modes,
The ordering constant is aB = ag = −1, as follows from the anticommutator
There is an anomaly in the gauge symmetry when cm 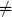 26, so we expect some breakdown in the BRST formalism. The BRST current is still conserved: all of the terms in the current (4.3.3) are analytic for any value of the central charge. However, it is no longer nilpotent,
26, so we expect some breakdown in the BRST formalism. The BRST current is still conserved: all of the terms in the current (4.3.3) are analytic for any value of the central charge. However, it is no longer nilpotent,
The shortest derivation of this uses the Jacobi identity, exercise 4.3. More directly it follows from the OPE
This requires a bit of calculation, being careful about minus signs from anticommutation. The single pole implies that {QB, QB} = 0 when cm = 26. Note also the OPE
which implies that jB is a tensor only when cm = 26.
Let us point out some important features. The missing equation of motion is just the vanishing of the generator Tab of the conformal transformations, the part of the local symmetry group not fixed by the gauge choice. This is a general result. When the gauge conditions fix the symmetry completely, one can show that the missing equations of motion are trivial due to the gauge invariance of the action. When they do not, so that there is a residual symmetry group, the missing equations of motion require its generators to vanish. They must vanish in the sense (4.1.2) of matrix elements, or more generally in the BRST sense. Denote the generators of the residual symmetry group by GI. The GI are called constraints; for the string these are Lm and 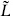 m. They form an algebra
m. They form an algebra
Associated with each generator is a pair of ghosts, bI and cI, where
The general form of the BRST operator, as illustrated by the string case (4.3.7), is
where 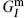 is the matter part of GI and
is the matter part of GI and
is the ghost part. The 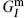 and
and 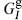 satisfy the same algebra (4.3.12) as the GI. Using the commutators (4.3.12) and (4.3.13), one finds
satisfy the same algebra (4.3.12) as the GI. Using the commutators (4.3.12) and (4.3.13), one finds
The last equality follows from the GGG Jacobi identity, which requires gKIJgMKL to vanish when antisymmetrized on IJL. We have neglected central charge terms; these need to be checked by hand.
To reiterate, a constraint algebra is a world-sheet symmetry algebra that is required to vanish in physical matrix elements. When we go on to generalize the bosonic string theory in volume two, it will be easiest to do so directly in terms of the constraint algebra, and we will write the BRST charge directly in the form (4.3.14).
BRST cohomology of the string
Let us now look at the BRST cohomology at the lowest levels of the string. The inner product is defined by specifying
In particular, the Hermiticity of the BRST charge requires that the ghost fields be Hermitean as well. The Hermiticity of the ghost zero modes forces the inner products of the ground state to take the form
Here |0;k  denotes the matter ground state times the ghost ground state |↓
denotes the matter ground state times the ghost ground state |↓ , with momentum k. The c0 and
, with momentum k. The c0 and 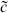 0 insertions are necessary for a nonzero result. For example,
0 insertions are necessary for a nonzero result. For example,  = 0; the last equality follows because b0 annihilates both the bra and the ket. The factor of i is needed in the ghost zero-mode inner product for Hermiticity. Inner products of general states are then obtained, as in the earlier calculation (4.1.13), by use of the commutation relations and the adjoints (4.3.17).
= 0; the last equality follows because b0 annihilates both the bra and the ket. The factor of i is needed in the ghost zero-mode inner product for Hermiticity. Inner products of general states are then obtained, as in the earlier calculation (4.1.13), by use of the commutation relations and the adjoints (4.3.17).
We will focus on the open string; the closed string discussion is entirely parallel but requires twice as much writing. As in the point-particle case (4.2.33), we will assert (and later show) that physical states must satisfy the additional condition
This also implies
since QB and b0 both annihilate 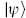 . The operator L0 is
. The operator L0 is
where
Thus the L0 condition (4.3.20) determines the mass of the string. BRST invariance, with the extra condition (4.3.19), implies that every string state is on the mass shell. We will denote by 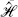 the space of states satisfying the conditions (4.3.19) and (4.3.20). From the commutators {QB, b0} = L0 and [QB, L0] = 0, it follows that QB takes
the space of states satisfying the conditions (4.3.19) and (4.3.20). From the commutators {QB, b0} = L0 and [QB, L0] = 0, it follows that QB takes 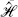 into itself.
into itself.
The inner product (4.3.18a) is not quite the correct one to use in 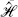 . It is not well defined: the ghost zero modes give zero, while the
. It is not well defined: the ghost zero modes give zero, while the  26(k − k′) contains a factor
26(k − k′) contains a factor  (0) because the momentum support is restricted to the mass shell. Therefore we use in
(0) because the momentum support is restricted to the mass shell. Therefore we use in 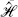 a reduced inner product
a reduced inner product  ||
||  in which we simply ignore the X0 and ghost zero modes. It is this inner product that will be relevant for the probabilistic interpretation. One can check that QB is still Hermitean with the reduced inner product, in the space
in which we simply ignore the X0 and ghost zero modes. It is this inner product that will be relevant for the probabilistic interpretation. One can check that QB is still Hermitean with the reduced inner product, in the space 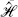 . Note that the mass-shell condition determines k0 in terms of the spatial momentum k (we focus on the incoming case, k0 > 0), and that we have used covariant normalization for states.
. Note that the mass-shell condition determines k0 in terms of the spatial momentum k (we focus on the incoming case, k0 > 0), and that we have used covariant normalization for states.
Let us now work out the first levels of the D = 26 flat spacetime string. At the lowest level, N = 0, we have
This state is invariant,
because every term in QB contains either lowering operators or L0. This also shows that there are no exact states at this level, so each invariant state corresponds to a cohomology class. These are just the states of the tachyon. The mass-shell condition is the same as found in the light-cone quantization of section 1.3 and from the open string vertex operators in section 3.6. The tachyon mass-squared, determined in a heuristic way in chapter 1, is here fixed by the normal ordering constant in QB, which is determined by the requirement of nilpotence.
At the next level, N = 1, there are 26 + 2 states,
depending on a 26-vector e and two constants,
and two constants, 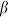 and
and  . The norm of this state is
. The norm of this state is
Going to an orthogonal basis, there are 26 positive-norm states and 2 negative-norm states. The BRST condition is
The terms proportional to c0 sum to zero by the mass-shell condition, and are omitted. An invariant state therefore satisfies k · e = 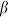 = 0. There are 26 linearly independent states remaining, of which 24 have positive norm and 2 have zero norm, being orthogonal to all physical states including themselves. The zero-norm invariant states are created by c−1 and k ·
= 0. There are 26 linearly independent states remaining, of which 24 have positive norm and 2 have zero norm, being orthogonal to all physical states including themselves. The zero-norm invariant states are created by c−1 and k ·  −1. A general |
−1. A general |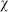
 is of the same form (4.3.25) with constants
is of the same form (4.3.25) with constants  , so the general BRST-exact state at this level is
, so the general BRST-exact state at this level is
Thus the ghost state c−1|0;k is BRST-exact, while the polarization is transverse with the equivalence relation
is BRST-exact, while the polarization is transverse with the equivalence relation 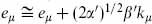 . This leaves the 24 positive-norm states expected for a massless vector particle, in agreement with the light-cone quantization and with the OCQ at A = –1.
. This leaves the 24 positive-norm states expected for a massless vector particle, in agreement with the light-cone quantization and with the OCQ at A = –1.
This pattern is general: there are two extra positive-norm and two extra negative-norm families of oscillators, as compared to the light-cone quantization. The physical state condition eliminates two of these and leaves two combinations with vanishing inner products. These null oscillators are BRST-exact and are removed by the equivalence relation.
An aside: the states b−1|0;k and c−1|0;k
and c−1|0;k can be identified with the two Faddeev–Popov ghosts that appear in the BRST-invariant quantization of a massless vector field in field theory. The world-sheet BRST operator acts on these states in the same way as the corresponding spacetime BRST operator in gauge field theory. Acting on the full string Hilbert space, the open string BRST operator is then some infinite-dimensional generalization of the spacetime gauge theory BRST invariance, while the closed string BRST operator is a generalization of the spacetime general coordinate BRST invariance, in the free limit.
can be identified with the two Faddeev–Popov ghosts that appear in the BRST-invariant quantization of a massless vector field in field theory. The world-sheet BRST operator acts on these states in the same way as the corresponding spacetime BRST operator in gauge field theory. Acting on the full string Hilbert space, the open string BRST operator is then some infinite-dimensional generalization of the spacetime gauge theory BRST invariance, while the closed string BRST operator is a generalization of the spacetime general coordinate BRST invariance, in the free limit.
The generalization to the closed string is straightforward. We restrict attention to the space 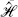 of states satisfying 1
of states satisfying 1
implying also
In the closed string,
Repeating the earlier exercise, we find at m2 = −4/ ′ the tachyon, and at m2 = 0 the 24 × 24 states of the graviton, dilaton, and antisymmetric tensor.
′ the tachyon, and at m2 = 0 the 24 × 24 states of the graviton, dilaton, and antisymmetric tensor.
4.4 The no-ghost theorem
In this section we prove that the BRST cohomology of the string has a positive inner product and is isomorphic to the light-cone and OCQ spectra. We are identifying the BRST cohomology as the physical Hilbert space. We will also need to verify, in our study of string amplitudes, that the amplitudes are well defined on the cohomology (that is, that equivalent states have equal amplitudes) and that the S-matrix is unitary within the space of physical states.
We will work in the general framework described at the end of chapter 3. That is, the world-sheet theory consists of d free X fields including
fields including 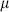 = 0, plus some compact unitary CFT K of central charge 26 − d, plus the ghosts. The Virasoro generators are a sum
= 0, plus some compact unitary CFT K of central charge 26 − d, plus the ghosts. The Virasoro generators are a sum
By compact we mean that 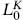 has a discrete spectrum. For example, in the case that K corresponds to strings on a compact manifold, the term
has a discrete spectrum. For example, in the case that K corresponds to strings on a compact manifold, the term  ′ p2 in L0 is replaced by the Laplacian −
′ p2 in L0 is replaced by the Laplacian −  ′∇2, which has a discrete spectrum on a compact space.
′∇2, which has a discrete spectrum on a compact space.
The general state is labeled
in the open and closed strings respectively, where N (and 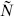 ) refer to both the d-dimensional and ghost oscillators, k is the d-momentum, and I labels the states of the compact CFT with given boundary conditions. The b0 condition (4.3.19) or (4.3.29) is imposed as above, implying the mass-shell condition
) refer to both the d-dimensional and ghost oscillators, k is the d-momentum, and I labels the states of the compact CFT with given boundary conditions. The b0 condition (4.3.19) or (4.3.29) is imposed as above, implying the mass-shell condition
for the open string and
for the closed string. That is, the contributions of the d ≤ 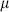 ≤ 25 oscillators are replaced by the eigenvalue of
≤ 25 oscillators are replaced by the eigenvalue of 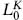 or
or 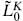 from the compact CFT. The only information we use about the compact CFT is that it is conformally invariant with the appropriate central charge, so there is a nilpotent BRST operator, and that it has a positive inner product. The basis I can be taken to be orthonormal, so the reduced inner products are
from the compact CFT. The only information we use about the compact CFT is that it is conformally invariant with the appropriate central charge, so there is a nilpotent BRST operator, and that it has a positive inner product. The basis I can be taken to be orthonormal, so the reduced inner products are
Now let us see what we expect for the physical Hilbert space. Define the transverse Hilbert space 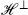 to consist of those states in
to consist of those states in 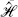 that have no longitudinal (X0, X1, b, or c) excitations. Since these oscillators are the source of the indefinite inner product,
that have no longitudinal (X0, X1, b, or c) excitations. Since these oscillators are the source of the indefinite inner product, 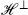 has a positive inner product. Light-cone gauge-fixing eliminates the longitudinal oscillators directly — the light-cone Hilbert space is isomorphic to
has a positive inner product. Light-cone gauge-fixing eliminates the longitudinal oscillators directly — the light-cone Hilbert space is isomorphic to 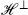 , as one sees explicitly in the flat-spacetime case from chapter 1. We will show, in the general case, that the BRST cohomology is isomorphic to
, as one sees explicitly in the flat-spacetime case from chapter 1. We will show, in the general case, that the BRST cohomology is isomorphic to 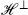 . That is, it has the same number of states at each mass level, and has a positive inner product. This is the no-ghost theorem.
. That is, it has the same number of states at each mass level, and has a positive inner product. This is the no-ghost theorem.
Proof
The proof has two parts. The first is to find the cohomology of a simplified BRST operator Q1, which is quadratic in the oscillators, and the second is to show that the cohomology of the full QB is identical to that of Q1. Define the light-cone oscillators
which satisfy
We will use extensively the quantum number
The number Nlc counts the number of — excitations minus the number of + excitations; it is not a Lorentz generator because the center-of-mass piece has been omitted. We choose a Lorentz frame in which the momentum component k+ is nonzero.
Now decompose the BRST generator using the quantum number Nlc:
where Qj changes Nlc by j units,
Also, each of the Qj increases the ghost number Ng by one unit:
Expanding out 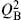 = 0 gives
= 0 gives
Each group in parentheses has a different Nlc and so must vanish separately. In particular, Q1 itself is nilpotent, and so has a cohomology.
Explicitly,
For m < 0 this destroys a + mode and creates a c, and for m > 0 it creates a — mode and destroys a b. One can find the cohomology directly by considering the action of Q1 in the occupation basis. We will leave this as an exercise, and instead use a standard strategy which will also be useful in generalizing to QB. Define
The normal ordering constant is determined by noting that Q1 and R both annihilate the ground state. Note that Q1 commutes with S. We can then calculate the cohomology within each eigenspace of S, and the full cohomology is the union of the results. If |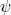
 is Q1-invariant with
is Q1-invariant with 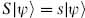 , then for nonzero s
, then for nonzero s
and so |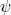
 is actually Q1-exact. Therefore the Q1 cohomology can be nonzero only at s = 0. By the definition (4.4.15) of S, the s = 0 states have no longitudinal excitations — the s = 0 space is just
is actually Q1-exact. Therefore the Q1 cohomology can be nonzero only at s = 0. By the definition (4.4.15) of S, the s = 0 states have no longitudinal excitations — the s = 0 space is just 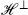 . The operator Q1 annihilates all states in
. The operator Q1 annihilates all states in 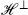 , so they are all Q1-closed and there are no Q1-exact states in this space. Therefore the cohomology is
, so they are all Q1-closed and there are no Q1-exact states in this space. Therefore the cohomology is 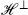 itself. We have proven the no-ghost theorem, but for the operator Q1, not QB.
itself. We have proven the no-ghost theorem, but for the operator Q1, not QB.
The proof had two steps, the first being to show that the cohomology could only come from s = 0 states (the kernel of S), and the second to show that s = 0 states were Q1-invariant. It is useful to prove the second step in a more abstract way, using the property that all s = 0 states have the same ghost number, in this case −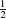 . Suppose S|
. Suppose S|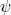
 = 0. Since S and Q1 commute we have
= 0. Since S and Q1 commute we have
The state |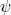
 has ghost number −
has ghost number −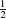 , so Q1|
, so Q1|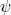
 has ghost number +
has ghost number +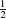 . Since S is invertible at this ghost number, it must be that Q1|
. Since S is invertible at this ghost number, it must be that Q1|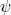
 = 0 as we wished to show.
= 0 as we wished to show.
It remains to show that the cohomology of QB is the same as the cohomology of Q1. The idea here is to use in place of S the operator
Now, U = {Q0+Q−1, R} lowers Nlc by one or two units. In terms of Nlcy, S is diagonal and U is lower triangular. By general properties of lower triangular matrices, the kernel of S + U can be no larger than the kernel of its diagonal part S. In fact they are isomorphic: if |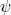 0
0 is annihilated by S, then
is annihilated by S, then
is annihilated by S + U. The factors of S−1 make sense because they always act on states of Nlc < 0, where S is invertible. For the same reason, S + U is invertible except at ghost number −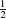 . Eqs. (4.4.16) and (4.4.17) can now be applied to QB, with S + U replacing S. They imply that the QB cohomology is isomorphic to the kernel of S + U, which is isomorphic to the kernel of S, which is isomorphic to the cohomology of Q1, as we wished to show.
. Eqs. (4.4.16) and (4.4.17) can now be applied to QB, with S + U replacing S. They imply that the QB cohomology is isomorphic to the kernel of S + U, which is isomorphic to the kernel of S, which is isomorphic to the cohomology of Q1, as we wished to show.
We must still check that the inner product is positive. All terms after the first on the right-hand side of eq. (4.4.19) have strictly negative Nlc. By the commutation relations, the inner product is nonzero only between states whose Nlc adds to zero. Then for two states (4.4.19) in the kernel of S + U,
The positivity of the inner product on the kernel of S + U then follows from that for the kernel of S, and we are done.
After adding the tilded operators to QB, Nlc, R, etc., the closed string proof is identical.
BRST–OCQ equivalence
We now prove the equivalence
To a state |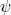
 in the matter Hilbert space, associated the state
in the matter Hilbert space, associated the state
from the full matter plus ghost theory. Again the ghost vacuum |↓ is annihilated by all of the ghost lowering operators, bn for n ≥ 0 and cn for n > 0. Acting with QB,
is annihilated by all of the ghost lowering operators, bn for n ≥ 0 and cn for n > 0. Acting with QB,
All terms in QB that contain ghost lowering operators drop out, and the constant in the n = 0 term is known from the mode expansion of QB, eq. (4.3.7). Each OCQ physical state thus maps to a BRST-closed state. The ordering constant A = −1 arises here from the L0 eigenvalue of the ghost vacuum.
To establish the equivalence (4.4.21), we need to show more. First, we need to show that we have a well-defined map of equivalence classes: that if 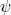 and
and 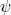 ′ are equivalent OCQ physical states, they map into the same BRST class:
′ are equivalent OCQ physical states, they map into the same BRST class:
must be BRST-exact. By (4.4.23), this state is BRST-closed. Further, since |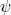
 ′ – |
′ – |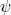
 is OCQ null, the state (4.4.24) has zero norm. From the BRST no-ghost theorem, the inner product on the cohomology is positive, so a zero-norm closed state is BRST-exact, as we needed to show.
is OCQ null, the state (4.4.24) has zero norm. From the BRST no-ghost theorem, the inner product on the cohomology is positive, so a zero-norm closed state is BRST-exact, as we needed to show.
To conclude that we have an isomorphism, we need to show that the map is one-to-one and onto. One-to-one means that OCQ physical states 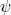 and
and 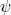 ′ that map into the same BRST class must be in the same OCQ class — if
′ that map into the same BRST class must be in the same OCQ class — if
then |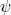
 – |
– |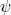
 ′ must be OCQ null. To see this, expand
′ must be OCQ null. To see this, expand
|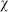
 has ghost number −
has ghost number −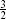 , so the ellipsis stands for terms with at least one c and two b excitations. Insert this into the form (4.4.25) and keep on both sides only terms with the ghost ground state. This gives
, so the ellipsis stands for terms with at least one c and two b excitations. Insert this into the form (4.4.25) and keep on both sides only terms with the ghost ground state. This gives
Terms with ghost excitations must vanish separately, and so have been omitted. Thus, 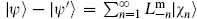 is OCQ null, and the map is one-to-one.
is OCQ null, and the map is one-to-one.
Finally, we must show that the map is onto, that every QB class contains at least one state of the form (4.4.22). In fact, the specific representatives (4.4.19), the states annihilated by S + U, are of this form. To see this, consider the quantum number N′ = 2N− + Nb + Nc, involving the total numbers of −, b, and c excitations. The operator R has N′ = −1: terms in R with m > 0 reduce Nc by one unit and terms with m < 0 reduce N− by one unit and increase Nb by one unit. Examining Q0 + Q−1, one finds various terms with N′ = 1, but no greater. So U = {R, Q0 + Q−1} cannot increase N′. Examining the state (4.4.19), and noting that S and |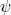 0
0 have N′ = 0, we see that all terms on the right-hand side have N′ ≤ 0. By definition N′ is nonnegative, so it must be that N′|
have N′ = 0, we see that all terms on the right-hand side have N′ ≤ 0. By definition N′ is nonnegative, so it must be that N′|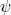
 = 0. This implies no −, b, or c excitations, and so this state is of the form (4.4.22). Thus the equivalence (4.4.21) is shown.
= 0. This implies no −, b, or c excitations, and so this state is of the form (4.4.22). Thus the equivalence (4.4.21) is shown.
The full power of the BRST method is needed for understanding the general structure of string amplitudes. However, for many practical purposes it is a great simplification to work with the special states of the form |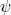 , ↓
, ↓ , and so it is useful to know that every BRST class contains at least one state in which the ghost modes are unexcited. We will call these OCQ-type states.
, and so it is useful to know that every BRST class contains at least one state in which the ghost modes are unexcited. We will call these OCQ-type states.
The OCQ physical state condition (4.1.5) requires that the matter state be a highest weight state with L0 = 1. The corresponding vertex operator is a weight-1 tensor field 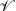 m constructed from the matter fields. Including the ghost state |↓
m constructed from the matter fields. Including the ghost state |↓ , the full vertex operator is c
, the full vertex operator is c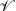 m. For the closed string the full vertex operator is
m. For the closed string the full vertex operator is 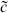 c
c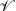 m with
m with 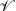 m a (1, 1) tensor. The matter part of the vertex operator is the same as found in the Polyakov formalism in section 3.6, while the ghost part has a simple interpretation that we will encounter in the next chapter.
m a (1, 1) tensor. The matter part of the vertex operator is the same as found in the Polyakov formalism in section 3.6, while the ghost part has a simple interpretation that we will encounter in the next chapter.
Eq. (4.4.19) defines an OCQ-physical state in each cohomology class. For the special case of flat spacetime this state can be constructed more explicitly by using the Del Giudice–Di Vecchia–Fubini (DDF) operators. To explain these we will need to develop some more vertex operator technology, so this is deferred to chapter 8.
Exercises
4.1 Extend the OCQ, for A = −1 and general D, to the second excited level of the open string. Verify the assertions made in the text about extra positive- and negative-norm states.
4.2 (a) In the OCQ, show that the state 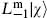 is physical (and therefore null) if |
is physical (and therefore null) if |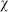
 is a highest weight state with
is a highest weight state with 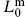 = 0.
= 0.
(b) Show that the state 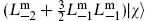 is physical and null if |
is physical and null if |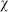
 is a highest weight state with
is a highest weight state with 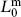 = −1.
= −1.
4.3 By writing out terms, demonstrate the Jacobi identity
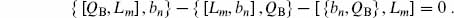
This is the sum of cyclic permutations, with commutators or anticommutators as appropriate, and minus signs from anticommutation. Use the Jacobi identity and the (anti)commutators (2.6.24) and (4.3.6) of bn with Ln and QB to show that {[QB, Lm], bn} vanishes when the total central charge is zero. This implies that [QB, Lm] contains no c modes. However, this commutator has Ng = 1, and so it must vanish: the charge QB is conformally invariant. Now use the QBQBbn Jacobi identity in the same way to show that QB is nilpotent when the total central charge is zero.
4.4 In more general situations, one encounters graded Lie algebras, with bosonic generators (fermion number FI even) and fermionic generators (FI odd). The algebra of constraints is
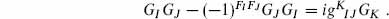
Construct a nilpotent BRST operator. You will need bosonic ghosts for the fermionic constraints.
4.5 (a) Carry out the BRST quantization for the first two levels of the closed string explicitly.
(b) Carry out the BRST quantization for the third level of the open string, m2 = 1/ ′.
′.
4.6 (a) Consider the operator 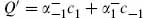 , obtained by truncating Q1 to the m = ±1 oscillators only. Calculate the cohomology of Q′ directly, by considering its action on a general linear combination of the states
, obtained by truncating Q1 to the m = ±1 oscillators only. Calculate the cohomology of Q′ directly, by considering its action on a general linear combination of the states
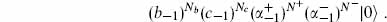
(b) Generalize this to the full Q1.
__________
1 S. Weinberg has pointed out that the simple argument given at the end of section 4.2 would only lead to the weaker condition 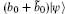 = 0. Nevertheless, we shall see from the detailed form of string amplitudes in chapter 9 that there is a projection onto states satisfying conditions (4.3.29).
= 0. Nevertheless, we shall see from the detailed form of string amplitudes in chapter 9 that there is a projection onto states satisfying conditions (4.3.29).