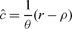
| 6 | Positional goods, climate change and the social returns to investment |
| Leila Davis and Peter Skott |
Climate change affects countries differently, and within regions the impact varies across groups. The time dimension introduces other distributional elements: the costs of global warming are borne (mainly) by future generations while the investment in mitigation may impose costs on the current generation.
The uneven distribution of costs and benefits is not unique to climate change and environmental policy. Policy generally benefits some people while others are hurt, and Pareto rankings of the outcomes are typically not available. Instead, decisions have to be based on social welfare evaluations that make (implicit or explicit) interpersonal comparisons, weighing up costs and benefits so as to arrive at a net result. The standard approach in the economic literature on climate change has been to use the utility function of “the representative agent” as a social welfare function.
The approach is in line with trends within macroeconomics where models based on an optimizing representative agent are ubiquitous. The models are seen as “micro-founded,” even though well-behaved preferences at the agent level fail to imply that aggregate outcomes behave as if they were generated by an optimizing representative agent, a result that has been well-known since the work of Debreu (1974), Mantel (1976) and Sonnenschein (1972). Abstracting from these existence problems, moreover, a welfare analysis based on the preferences of the representative agent can lead to systematic biases. In this chapter we focus on the intertemporal dimension and the biases that arise when consumption has a positional component. To simplify the analysis and highlight these particular effects, we disregard problems associated with intra-generational distribution and assume that all agents are identical with respectto both preferences and endowments; Skott and Davis (2012) examine biases that derive from intra-generational inequality.
The chapter is in five sections. The next section considers representative agents and the role of the rates of return. The third section introduces positional goods and sets up a small model to analyze how they affect the optimal amount of investment in mitigation. The fourth section relates the formal model to procedures used in climate models to evaluate the costs and benefits of mitigation, and presents the results of a small survey to evaluate the importance of the biases identified by the model. The final section summarizes the results and offers a few concluding remarks.
Consider a market economy and assume that the trajectories of aggregate consumption, investment and output can be described as if determined by an intertemporally optimizing representative agent. Given this highly restrictive assumption, it may seem reasonable to use the utility function of the representative agent as the social welfare function. Woodford (2003), for instance, suggests that the utility function of the representative agent “provides a natural objective in terms of which alternative policies should be evaluated” (12; emphasis added), while, according to Blanchard (2008), contemporary macro models with formal optimization enable one “to derive optimal policy based on the correct (within the model) welfare criterion” (9; emphasis added). Most tellingly, perhaps, the evaluation of outcomes based on the stipulated utility function of the representative agent is usually presented without any argument or caveat.1
Using this “descriptive” representative-agent approach, the social welfare function has to be calibrated to fit empirical observations.2 An optimizing representative agent in a standard discounted-utility model chooses a consumption path that satisfies the Euler equation
|
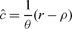(1) |
where c is consumption and a hat over a variable denotes a growth rate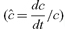 
; ρ is the pure rate of time preference, θ the intertemporal elasticity of substitution and r the real rate of return on saving. We have observations for r and ĉ, and the choices of the representative agent should match these observations. It follows that although the social welfare function has two parameters, θ and ρ, there is only one degree of freedom.
Most economic analyses of climate change have followed the descriptive approach. The Stern Review (Stern 2007) is an exception. Stern adopted a “prescriptive” approach to social welfare and argued that on ethical grounds the pure discount rate should be close to zero. He combined the low discount rate with a logarithmic specification of the instantaneous utility function (θ = 1), and this combination of parameters fuels the strong recommendations of the Stern Review.
Not surprisingly, Stern’s assumptions have been challenged. Nordhaus (2008) rejects Stern’s “lofty vantage point of the social planner” as being “misleading in the context of global warming and particularly as it informs the negotiations of policies among sovereign states” (174). Advocating a descriptive approach, Nordhaus wants to base the analysis on the revealed preferences of the representative agent. This approach, he argues, does not assume “the social desirability of the distribution of incomes over space or time under existing conditions.” Instead,
The calculations of changes in world welfare arising from efficient climate-change policies examine potential improvements within the context of the existing distribution of income and investments across space and time.
(Nordhaus 2008: 174–175)
There is an internal tension in Nordhaus’s defense of the descriptive approach. He also argues that
The individual rates of time preference, risk preference, and utility functions do not, in principle at least, enter into the discussion or arguments at all. An individual may have high time preference, or perhaps double hyperbolic discounting, or negative discounting, but this has no necessary connection with how social decisions weight different generations. Similar cautions apply to the consumption elasticity.
(172)
It seems inconsistent, however, to argue that there is “no necessary connection” between individual choice and the appropriate criteria for social decisions and, at the same time, insist on a descriptive representative-agent approach to social valuation. The rationale behind the descriptive approach is precisely that the representative agent describes the average behavior of the individuals; why insist on the descriptive approach if individual choices are irrelevant?
Leaving aside this inconsistency, Stern’s combination of a logarithmic utility function and a near-zero discount rate fails to meet the descriptive test if the annual real rate of return is taken to fall in a range that matches the observed return on private capital.3 More importantly, whatever one may think about ethics and the pure rate of discount, there is a tradeoff, Nordhaus argues, between investment in mitigation and investment in other areas including traditional capital, R&D, education, etc. If r measures the social rate of return to these conventional investment projects, investment in emissions reduction must get a similar return:
In choosing among alternative trajectories for emissions reductions, the key economic variable is the real return on capital, r, which measures the net yield on investments in capital, education, and technology. In principle, this is observable in the marketplace…. The return on capital is the discount rate that enters into the determination of the efficient balance between the cost of emissions reductions today and the benefit of reduced climate damages in the future. A high return on capital tilts the balance toward emissions reductions in the future, while a low return tilts reductions toward the present.
(Nordhaus 2008: 59)
According to Nordhaus, the Stern Review with its low discount rate for investment in abatement would misallocate investment to such an extent that an attempt to maintain the welfare of current generations “would leave the future absolutely worse off; it would be Pareto-deteriorating. The Stern Review’s approach is inefficient because it invests too much in low-yield abatement strategies too early” (180). Lookingatthis from another angle, the Sternparameters have implications for the optimal levels of conventional investment. Using these parameters and the observed values of the return to capital, the optimal global saving rate would be about twice the current level, an implication that does not, Nordhaus suggests, seem “ethically compelling” if global per capita consumption is expected to grow from around US$6,600 today to around US$87,000 in two centuries measured in constant 2005 dollars (Nordhaus 2008: 179).
This general argument has considerable appeal.4 But it relies on the implicit assumption that socially optimal trajectories require an expected rate of return to mitigation that is (approximately) equal to the observed private rate of return on capital. This assumption may be invalid. As pointed out by Weitzman (2007, 2009), the returns to mitigation may be high in bad states of the world, and this can dramatically reduce the appropriate discount rate for investment in abatement. Michl (2010) also comments on the use of the rate of return on private capital as the basis for discounting mitigation. He notes in particular the implications of the capital controversy for the identification of the rate of return on capital with a “marginal product of capital.” Hoel and Sterner (2007) consider the effects of changes in the relative price of environmental goods; an increasing relative price effectively reducing the discount rate. Like these contributions, our argument in this chapter focuses on the appropriate discount rate for investment in mitigation and, like Weitzman and Hoel and Sterner, we argue that it can be much lower than the private real rate of return. But the mechanism is different.5
Environmental externalities are not the only externalities. Utility derives not just, or even primarily, from absolute consumption, once a certain level has been reached. The level of consumption relative to other people and relative to own past consumption may be at least as important. A substantial literature has emphasized these effects,6 and the argument has empirical support. Recent empirical studies have shown a high correlation between relative income and reported well-being; prominent examples include Blanchflower and Oswald (2004) who examine data for the US and the UK, Luttmer (2005) with US data, and Fafchamps and Shilpi (2008) with data for Nepal. The use in these studies of reported “well-being” or “happiness” as a measure of utility raises many issues, but it would be hard to reject the influence of relative income and status on utility, and “happiness” studies are not the only source of empirical support.7 Johansson-Stenman, Carlson and Daruvala (2002) analyze experimental choices between hypothetical societies and find a strong concern for relative income. Evidence from the experimental and behavioral literature also suggest that “social preferences” shape the behavior of many people (Fehr and Schmidt 2003).
The relevance of status and relative income effects for economic policy has been examined by, among others Ng and Wang (1995) and Howarth (2000), but to our knowledge there have been no attempts to analyze the implications for climate change and the appropriate discount rate for investment in abatement.
Consider a simple two-period model. There are two goods, a standard good and an environmental good. The standard good (y) is a private good, but the consumption of this good involves a positional element, and increased consumption imposes a negative externality on other agents. We disregard the uneven distribution of the effects of climate change and treat the environmental good as a pure public good.
All agents are identical, and the preferences of an agent can be described by the following utility function
 |
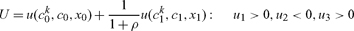(2) |
where u(.,.,.)is the per-period utility function; c is the consumption of the standard good and x the environmental good; superscripts k indicate agent and subscripts on a variable (0 or 1) indicate period; c–variables without a superscript refer to average consumption across all agents; by definition the consumption of the public environmental good x is uniform across agents.8
The standard good can be used for either consumption, conventional investment (i) or investment in abatement (m), and we assume
 |
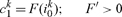(3) |
 |
(4) |
 |
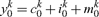(5) |
 |
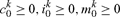(6) |
Note that agent k’s consumption of the standard good in period 1 depends on the agent’s own investment while the consumption of the environmental good is determined by aggregate conventional and abatement investment.9 The amounts y0 and x0 of the standard and environmental good that are available in period 0 are taken as exogenous, and all agents have the same initial endowment of the standard good (y0k = y0).
We now consider four different scenarios:
A: Business as usual
Without policy intervention, agents maximize (2) subject to (3), (5), and (6). It is readily seen that the solution has m0k = 0 and that it satisfies a standard Euler equation
 |
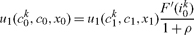(7) |
where subscripts on a function indicate partial derivatives (e.g. u1 = ∂u(c0k, c0, x0)/ ∂c0k). In equilibrium, cjk = cj and i0k = i0, and we have
 |
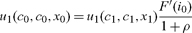(8) |
B: Addressing the environmental externality
A benevolent social planner should take into account both the environmental externalities (equation (4)) and the positional-good externality (u2 ≤ 0). But consider first the case in which the social planner overlooks the positional-good externality; that is, she mistakenly believes that u2 = 0.
Social welfare is given by
 |
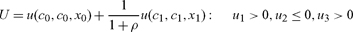(9) |
Maximizing (9) subject to (3)–(6) and the symmetry condition (cjk = cj, ijk = ij, mjk = mj), and setting u2 = 0, we get the following first-order conditions:
 |
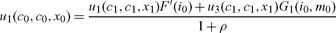(10) |
 |
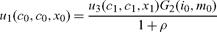(11) |
C: Addressing the positional-good externality
In this case, the social planner overlooks the environmental externality. Equation (4) is ignored and the values of both x0 and x1 are treated as exogenous. The planner therefore sets m0 = 0 and chooses i0, c0 to maximize (9) subject to (3), (5)–(6) and the symmetry condition.
The first-order condition in this case becomes
 |
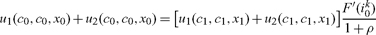(12) |
D: Addressing both environmental and positional-good externalities
The first-order conditions now take the following form:
 |
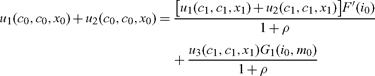(13) |
 |
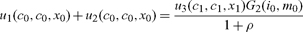(14) |
Comparing scenarios A and B, the climate externality tends to reduce the optimal amount of conventional investment (use equations (9) and (10) and note the negative impact of i0 on x1 via G1 in the numerator on the right-hand side of (10)), and equation (11) implies positive amounts of investment in mitigation if u3G2 is sufficiently high at m0 = 0. These are standard results.
The positional-good externality in scenario C may influence the optimal rate of investment, but in benchmark cases — including when u is CES — the optimal solution is identical to the one in the A scenario.10 The intuition behind this seemingly paradoxical result is that although the benefits from future increases in consumption are reduced by the externalities, so are the costs from the required reduction in consumption, and these cost and benefit effects offset each other.
Comparing cases B and D, however, it is apparent that the consumption externalities become important for optimal investment when environmental externalities are present too. Formally, this follows from the fact that the coefficients on G1 are the same on the right hand side of (10) and (13). Intuitively, the consumption externalities do not reduce the negative impact of current investment on future consumption of the environmental good and this reduces the optimal value of i0. The optimal investment in mitigation, on the other hand, is boosted by the reduction in the social cost of a reduction in the period-0 consumption of the standard good (equations (11) and (14) have the same right hand side but the left hand side has been reduced in (14)).
Consider a special case in which the standard and environmental goods are perfect substitutes. Thus, let
 |
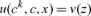(15) |
where
 |
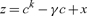(16) |
is the amount of “generalized consumption” and where it is assumed that v takes the standard CIES form.11
Using these specifications the first-order conditions – taking into account both consumption and environmental externalities – can be written
 |
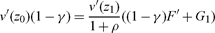(17) |
 |
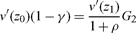(18) |
Hence, optimality requires that
 |
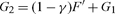(19) |
Equation (19) states the required equality between the social rates of return to the two types of investment. G2 = ∂z1/∂m0 is the return to investment in mitigation. The gross private return to conventional investment is given by ∂z1k /∂i0k = F′; including the environmental externality the social return is reduced to F′ + G1, and consumption externalities introduce an additional wedge: the social benefits of an increase in the consumption of the standard good is reduced by the factor 1 − γ.
Any mapping of this stylized two-period model into real-world decision problems raises problems, but equation (19) can be used to derive a quick back-of-the-envelope estimate of the magnitude of the positional-good effect. Thus, consider a period length of 50 years, let the annual private return to conventional investment be six per cent, and assume that this return is reduced to five per cent when the environmental externality is included (i.e. F′ = exp(rT) = exp(0.06 × 50), F′ + G1 = exp(0.05 × 50)). If γ = 0.5, equation (19) implies that the required annual return to environmental investment is 1.5 per cent,12 a value that is virtually identical to the one used by the Stern Review.13
The special case has wider relevance. Consider a more general specification of “generalized” consumption. Formally, let
 |
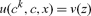(20) |
 |
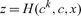(21) |
In terms of generalized consumption goods, the private return to conventional investment now is given by H1F′; taking into account the environmental externality, the return in terms of generalized consumption goods is H1F′ + H3G1, and when both externalities are included the return falls to (H1 + H2)F′ + H3G1. Optimality requires that this expression equal the return to investment in abatement, which, in terms of the generalized good, is now H3 G2.14 Formally, using (13)–(14) and (20)–(21), the first-order conditions imply
 |
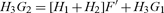(22) |
This optimality condition can be rewritten
 |
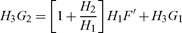(23) |
Equation (23) differs from (19) in two ways. The expressions for the returns in terms of generalized consumption, first, are slightly more complicated (H3 G1, H3G2,H1F′ instead of G1, G2,F′); this difference is of no significance. The ratio −H2/H1, secondly, takes the place of the constant γ. In equilibrium, however, we have ck = c and the ratio will be constant if H takes a standard CES form: if H(ck, c,x)= [α1(ck)δ − α2cδ + βxδ]1/δ we have
 |
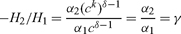(24) |
The benchmark case with γ = 0.5 is in line with the evidence. The empirical studies by Blanchflower and Oswald (2004), Luttmer (2005), and Fafchamps and Shilpi (2008) estimated a Cobb–Douglas utility function (a special case of the CES function),
 |
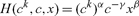(25) |
Blanchflower and Oswald (2004) obtained estimates for −H2/H1 of about 0.4 while Luttmer (2005) and Fafchamps and Shilpi (2008) found values of about 0.75 or higher. The experimental approach in Johansson-Stenman et al. (2002) gave estimates of about 0.35.
Our analysis of positional goods, it could be argued, does not necessarily invalidate a representative-agent approach. In fact, our model has been cast in terms of identical agents. But a representative-agent analysis easily goes wrong. Thus, assume for the sake of the argument that the model in this section gives an accurate picture of the economy. In equilibrium ck = c and the welfare of the representative-agent can be written as a reduced-form function of conventional and environmental consumption,
 |
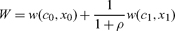(26) |
Using the descriptive approach and the general specification (26), it is required that the properties of the correct welfare function W match the observed behavior, that is, it is assumed that observed consumption patterns can be derived from maximizing W subject to the relevant constraints. This assumption is invalid. The patterns of actual consumption in the business-as-usual regime are the same no matter how strong is the consumption externality (the value of γ in the special case above), and this observational equivalence implies that the correct parameters in the welfare function cannot — as a matter of principle — be decided on the basis of the macroeconomic evidence. In this sense the “descriptive approach” is intrinsically flawed. Moreover, if (26) is fitted to the macroeconomic evidence, the positional externalities fail to be incorporated and the welfare conclusions will be systematically biased. Putting it differently, in equilibrium the correct representation of the social welfare may take the form (26) whether or not there are consumption externalities. But the calibration of (26) to the evidence is only legitimate in the absence of consumption externalities.
Climate change influences the production of some market goods – agricultural output is the obvious example – but many of its effects concern non-market “goods” like climate-related diseases. In order to incorporate environmental externalities into existing economic models, monetary values have to be determined for the non-market effects. These values are assigned by estimating either individuals’ willingness to pay for the environmental goods or their willingness to accept compensation for damages.
The estimates are based on either stated preference or revealed preference techniques. Revealed preference techniques use market information associated with the effect being evaluated to infer a monetary value – i.e. “surrogate markets” are used to value non-market environmental goods (Intergovernmental Panel on Climate Change (IPCC) 1996: 184). Hedonic wage studies, for example, use market information on wage differentials to derive estimates for the value of a statistical life. These market-based revealed preference techniques are limited in scope, as it is often difficult to find relevant market information with which to infer a monetary value for the non-market good or service in question. As such, costs and benefits are often estimated using the contingent valuation method, whereby monetary values are assigned according to individuals’ stated willingness to pay or willingness to accept compensation. Thus, the values depend on what individuals’ behavior would have been if markets for the environmental goods and services had existed – through what the IPCC terms “hypothetical markets” (184). Hypothetical markets reflect individuals’ responses to questions regarding their personal willingness to pay, and “monetary estimates are thus able to cover both market and nonmarket impacts” (183).
The procedure requires a delineation of the target population, i.e. those individuals must be identified that are affected by the environmental effect. Willingness to pay is estimated using surveys that directly ask respondents how much they are willing to pay, and these individual responses are aggregated to determine total willingness to pay, from which monetary values are inferred. The resulting evaluations can be questioned (see, for example, Venkatachalam 2004; Ackerman and Heinzerling 2004). Willingness to pay fundamentally reflects ability to pay, and the preferences and values of the rich are thus inherently overrepresented relative to those of the poor. At a more technical level, contingent valuation surveys suffer from potential biases arising from incentives to misrepresent preferences or from implied cues within the survey design that prompt certain responses (Mitchell and Carson 1989).15
The positional character of consumption can impart an additional bias: a higher willingness to pay can be expected if it is clarified that the reduction in consumption will be imposed on everyone.16 We carried out a simple survey to preliminarily investigate this hypothesis. The survey considers a particular environmental change. The subjects are informed that global warming and other environmental changes threaten the survival of some animal species and that, according to some estimates, as many as 25 per cent of all species will be extinct before 2100 under current trends. Policy intervention, it is added, may change the scenario and ensure the survival of these endangered species. The extinction of species was chosen as a simple and concrete example of a pure public good threatened by global warming.17
The presentation of the environmental problem — the extinction of the species — was followed by a willingness-to-pay question. We used three different versions of the question. In a first version, respondents were asked how large a proportion of their stream of current and future income they would be willing to give up in order to ensure that no existing species become extinct. A second version asked how large a proportion of current and future incomes should be given up to ensure that no existing species become extinct, now supposing that the costs of intervention are shared such that all incomes are reduced by the same percentage. These two questions highlight the difference between a single individual’s willingness to pay for environmental protection, and the willingness to pay for environmental protection when there is no relative loss in income. The purpose of the survey is not to value environmental goods or damages, but to investigate the role of positional effects in individuals’ willingness to pay. As such, what is important is not the exact loss that respondents are willing to accept to protect the environment, but any systematic differences between willingness to pay when costs are individual and when costs are shared.
The positional effect can be seen as an example of the role of reference points in the evaluation of outcomes. Other people’s consumption represents one such reference point; own past consumption is another reference point. Consumption is valued not just relative to other people’s consumption, but also in relation to own past consumption. The behavioral economics literature has documented the existence of loss aversion: people tend to place more value on avoiding losses than on acquiring gains (Tversky and Kahneman 1991). Loss aversion – while distinct from the positional effects that have been the focus of the previous three sections – has implications for the measurement of willingness to pay.
The first two versions of the willingness-to-pay question are framed in terms of levels, and it is possible that respondents interpreted the questions to require an absolute decline relative to their current income. If the cost of environmental protection is understood to require a level reduction in take-home pay, concerns regarding ability to meet other financial commitments such as mortgage payments or car payments may decrease willingness to pay. Onthe other hand, if the question is defined in terms of a lower future growth rate of income – implying smaller future income gains instead of a future income loss – loss aversion may not be expected to play a significant role, and we would expect an increased willingness to pay. A third version of the question therefore defined the issue in terms of reductions in the future growth rate of income. As in the second question, the losses are to be shared – everyone will experience the same reduction in future income growth – and the question is constructed such that the intervals describing reductions in the future growth rate of income roughly correspond to the intervals describing reductions in the level of the current and future income stream. Exact correspondence between levels and growth rates depends on the discount rate, the growth rate and the time horizon. Table 6.1 in the Appendix shows the growth reductions consistent with various parameters.18
The survey was carried out in March 2011. It was answered by a total of 496 students, 142 of whom received question one, 192 of whom received question two and 162 of whom received question three. The participants were University of Massachusetts students in large introductory classes on microeconomics and macroeconomics; teaching assistants administered the survey, and each discussion
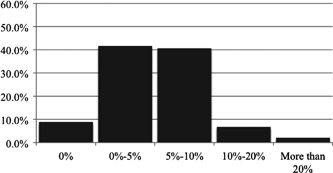
Figure 6.2 Responses to question 2.
section was randomly assigned one of the questions (all students in a section received the same question). The questions are reproduced in the Appendix.
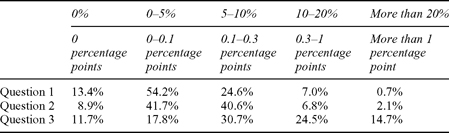
The first issue is whether individuals are more willing to give up income in order to protect the environment if the costs are shared and their relative position is maintained (the positional effect). To consider this issue, the relevant comparison is between the results of question 1 and question 2. As expected, the survey indicates that sharing increases the willingness to pay. When the loss is individual, approximately 54 per cent of respondents said that they would be willing to give up zero to five per cent of their current and future stream of income in order to prevent the extinction, while 25 per cent of respondents would be willing to give up five to ten per cent of their current and future income stream (see Figure 6.1). When the payment is to be shared, on the other hand, the percentage of respondents who were willing to give up five to ten per cent of current and future incomes increases to 41 per cent (see Figure 6.2). Thus, the standard estimates of willingness to pay for environmental goods used in climate change analysis may be skewed downwards.
The results may support the existence of positional externalities in consumption. The outcome may also, however, be interpreted to indicate other effects including, importantly, concerns about fairness.19 The distinction between positionality and fairness concerns will be important for some purposes, but the implications for the valuation of environmental goods is similar: there will be a higher willingness to pay when costs are shared.
Figure 6.3 shows the responses to the third version of the question (effects of loss aversion). Only 18 per cent of respondents said that 0 to 0.1 percentage points of income growth should be given up to ensure the survival of species endangered by climate change (corresponding to a zero to five per cent reduction in future levels of income) — a rate considerably lower than with either of the two previous questions. In contrast, 31 per cent of respondents would be willing to accept a 0.1 to 0.3 percentage point reduction in future income growth (corresponding to a five to ten per cent reduction in future levels of income), and 25 per cent of respondents would be willing to accept a 0.3 to one percentage point reduction in future income growth (corresponding to a 10 to 20 per cent reduction in future levels of income). To investigate whether the results indicate loss aversion, we can then compare these results from question 3 with those of question 2. In the second question (in which the costs are to be shared and the question is asked in terms of levels), while 41 per cent of respondents thought we should give up five to ten per cent of future income growth to prevent the extinction, only seven per cent of respondents were willing to give up 10 to 20 per cent of future income. Finally, while approximately two per cent of respondents were willing to give up more than 20 per cent of future incomes to prevent the environmental damage, 15 per cent of respondents were willing to make the corresponding payment when the question was defined in terms of growth rates. The responses to questions 2 and 3, therefore, suggest that consumption externalities operate through loss aversion (and, thus, through taking ones own income as a reference point) in addition to through positional effects relative to others.
As the objective of the survey is not to determine a monetary value for the species that potentially face extinction as a consequence of climate change, the exact intervals in the questions are unimportant. The important point is that the results indicate a significantly higher willingness to pay for environmental protection when the costs are to be shared equally among the population and thus entail no relative loss in income; and, furthermore, that this higher willingness to pay is even more substantial when the costs take the form of slower future growth rather than a level reduction in current and future incomes. The mean and median responses to question 3 are more than double those to question 1.20
It is sometimes suggested that the science behind climate change may be weak, but that the economics in the integrated assessment models is well-established and sound. We are not in position to evaluate the science but well-established as it may be, the economics is questionable. Weitzman (2009) has emphasized the treatment of catastrophic risk, and Rezai, Foley and Taylor (2012) and Ackerman, Stanton and Bueno (2010) find that changes in some of the specifications give results that are dramatically different from those of Tol and Nordhaus.
This chapter has raised a different concern. Consumption externalities associated with positional goods and status concerns are well-documented. Using a simple two-period model we have shown that the interaction between these consumption externalities and environmental externalities has implications for the appropriate discount rate: the required return on investment in mitigation is lower than the private return to conventional investment. The magnitude of the difference depends on the weight of positional consumption in utility. An empirical literature has examined this question, and using estimates from this literature, the effect on the appropriate discount rate is quantitatively highly significant. This conclusion finds support in our survey of willingness to pay. Subjects show a much greater willingness to pay when the costs are shared and when the costs are expressed in terms of lower future growth, rather than in reductions in the level of income. Overall, the results suggest that incorporation of consumption externalities into climate change analysis may have important implications for the calculation of the social costs and benefits of mitigation. By ignoring consumption externalities, the existing integrated assessment models produce an inflated estimate of the optimal level of greenhouse gas emissions today.
The argument has been cast within a standard optimal-growth framework. It is not obvious, however, that this framework should dominate the discussion. The appropriateness of autilitarian approach in general and the specific version used by the integrated assessment models can be challenged.21 The issues are beyond the scope of this chapter, and we do not pretend to have answers. It can be a problem, however, if an influential discipline makes strong recommendations based on a questionable but seemingly “objective” set of ethical principles. The problem is compounded if the recommendations are couched in a mathematical formalism that makes it hard for outsiders to follow the analysis.
An earlier version of this chapter was presented at the Analytical Political Economy Workshop, Queen Mary University of London, May 2011, and at the Adam Smith Seminar, University of Hamburg. We thank the participants and Frank Ackerman, Jim Boyce, Alex Coram, Liz Stanton and Roberto Veneziani for helpful comments and suggestions. We are grateful also to two anonymous referees whose constructive comments led to significant improvements in this version of the chapter.
1 Nordhaus (2008, 39) simply comments that
policies are chosen to maximize a social welfare function that is the discounted sum of the population-weighted utility of per capita consumption. Equation (A.1) is the mathematical statement of the objective function. This representation is a standard one in modern theories of optimal economic growth.
2 The “prescriptive”/“descriptive” terminology is used by Arrow et al. (IPCC, 1996).
3 This is the range used by Nordhaus (2008); see e.g. p. 57.
4 The argument appears to be in line with Rezai et al. (2012). The pure discount rate and the tradeoff between current and future generations are not nearly as important as is commonly believed, they argue. The real question is whether the composition of investment should be changed, and starting from a business-as-usual case in which all investment is guided by private profit, the answer is yes: addressing the climate externality can lead to Pareto improvements if some investment is re-directed from conventional areas to mitigation.
5 The discount rate is not the only variable that matters for optimal mitigation. The specification of the damage function can produce dramatic effects on optimal mitigation. Thus, Rezai et al. (2012) use a version in which the proportional effect on output of an increase in atmospheric CO2 goes to infinity as the CO2 concentration approaches a finite level (which is set at just over twice the current level in their simulations). This assumption, which is quite different from the specifications in DICE (the Dynamic Integrated model of Climate and the Economy developed by Nordhaus), contributes to the contrast between their findings and those of Nordhaus. As pointed out by Weitzman (2009: 16) the damages at high CO2 concentrations are typically found by extrapolation using a functional form that is largely arbitrary, and there is little justification for the standard versions.
Ackerman et al. (2010) modify the standard Nordhaus-type assumptions in another direction by respecifying the costs of abatement, using estimates from a study by McKinsey & Co.
6 The contributions include Veblen (1899), Duesenberry (1949), Hirsch (1977), Easterlin (1974, 2001), Sen (1983) and Frank (1985, 2005).
7 Frey and Stutzer (2002) survey the behavioral literature on “happiness.”
8 Veblen effects are commonly represented by a utility function of the form
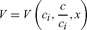
Without restrictions on the partial derivatives, this alternative representation is equivalent to the specification in (2). The standard Veblen assumptions −V1 > 0,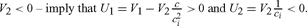 
9 Climate change need not enter purely as a public good. It also affects the production of some conventional goods; agricultural goods, for instance. In terms of the model, these effects could be captured by including the state of the environment as an argument in the production function for the private good:
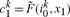
This extension of the model would complicate some of the expressions but leave the qualitative results unchanged.
10 The conditions (8) and (12) are equivalent if there is a constant λ such that
u2(c,c,x) = λu1(c,c,x)
for all c, x. This condition is met for the CES specification of u,
u = [α1(ck)δ − α2cδ + βxδ]1/δ
11 The unit coefficient on ci and x can be obtained by an appropriate choice of units. Thus, there is no loss of generality in using (16) rather than z = αci − γc + βx.
12 Solve the equation
exp(rm × 50) = (1 − γ)F′ + G1
13 Stern’s benchmark assumptions are ρ = 0.1%,θ = 1 and ĉ = 1.3%, with an implied r-value of 1.4.
Note, however, that according to the positional-goods argument, abatement benefits that take the form of increased production of positional goods should not be discounted at the low rate.
14 Strictly speaking, these expressions give the returns in terms of generalized consumption to the investment of one unit of the standard good. The return to the investment of one unit of the generalized good can be obtained by adjusting the expressions using the common factor (∂z0/∂c)−1.
15 The IPCC notes that, “although controversial, these approaches are well established in the literature” (184). Similarly, Nordhaus’s estimates of the impacts of climate change rely on a willingness to pay approach (Nordhaus and Boyer 2000: 71). While Nordhaus writes that valuation techniques with “an objective behavioral component, whether in market prices or individual actions” are generally preferable since “Valuation techniques that are largely subjective – such as contingent valuation – are difficult to validate,” he also notes that techniques like contingent valuation are “needed in some areas” (Nordhaus 2006a: 151). Impacts – which are calculated by sector – are estimated through an impact index that represents “the fraction of annual output that subregion j would be willing to pay to avoid the consequences on sector i of a temperature increase of T°C” (73). These impacts are then used to estimate the damage functions, which indicate the per cent loss in output at different levels of global temperature increase. Thus, while many impacts are measured using surrogate markets, hypothetical markets and contingent valuation remain a commonly used method by which to evaluate and incorporate non-market costs of climate change into analysis.
16 Evidence based on actual behavior – e.g. wage premia for risky jobs as an indicator of the value of life – also suffers from this bias. It reflects individual behavior which (by definition) does not internalize the externalities associated with positional goods.
17 While some respondents commented that they did not have a high willingness to pay because some threatened species are likely to be entirely irrelevant to their own future wellbeing, use of a more dramatic example (that may enter more directly into respondents’ utility functions) is likely to detract from and complicate the interpretation of the results. We wanted a climate effect that is well-defined and that has a clear public-good character.
18 The upper limits in the growth formulation are somewhat higher than in the level formulation for most reasonable parameters. This choice was deliberate. Since we expect higher willingness to pay in the case of growth reductions, responses to the third question that are concentrated in the upper intervals are consistent with an even greater willingness to pay for environmental protection in the context of growth rather than level reductions – i.e. the bias incorporated in the intervals would further support the hypothesis.
19 These results may also indicate other effects including, for example, a “small number effect” if respondents feel that a 0–0.1 percentage points decline in income growth is small relative to the equivalent loss in income levels.
20 Assuming a uniform distribution within each interval and setting ρ − g = 3%, the means are 4.46, 5.7 and 10.8, respectively, for questions 1, 2 and 3.
21 Economists are aware that there are alternative ethical principles. Nordhaus (2006b: 8) for instance, points out that “it should be clear that alternative ethical perspectives are possible. Moreover, as I suggest below, alternative perspectives provide vastly different prescriptions about desirable climate change policies.” The actual analysis and recommendations, however, are almost invariably based on welfare functions associated with representative-agent models. Sen (1982) is an exception. He suggests that future generations have a right to a non-degraded environment and rejects the “welfarism” of the standard analysis.
Ackerman, F. and Heinzerling, L. (2004) Priceless: On Knowing the Price of Everything and the Value of Nothing. The New Press, New York.
Ackerman, F., Stanton, E., and Bueno, R. (2010) “CRED: A new model of climate and development”. DESA Working Paper No. 96, United Nations Department of Economic and Social Affairs.
Blanchard, O. (2008) “The state of macro”. NBER working paper 14259, http://www.nber.org/papers/w14259.
Blanchflower, D., and Oswald, A. (2004) “Well-being over time in Britain and the USA”. Journal of Public Economics, 88(7–8): 1359–1386.
Debreu, G. (1974) “Excess demand functions”. Journal of Mathematical Economics, 1(1): 15–21.
Duesenberry, J. (1949) Income, Saving and the Theory of Consumer Behavior. Harvard University Press, Cambridge.
Easterlin, R. (1974) “Does economic growth improve the human lot? Some empirical evidence”. In Nations and Households in Economic Growth: Essays in Honor of Moses Abramovitz, R. David and M. Reder (eds.). Academic Press, New York, pp. 89–125.
Easterlin, R. (2001) “Income and happiness, towards a unified theory”. The Economic Journal, 111(473): 465–484.
Fafchamps, M., and Shilpi, F. (2008) “Subjective welfare, isolation, and relative consumption”. Journal of Development Economics, 86(1): 43–60.
Fehr, E., and Schmidt, K. (2003) “Theories of Fairness and Reciprocity — Evidence and Economic Applications”. In M. Dewatripont, L. Hansen and St. Turnovsky (eds.), Advances in Economics and Econometrics — 8th World Congress, Econometric Society Monographs, Cambridge, Cambridge University Press.
Frank, R. (1985) “The demand for unobservable and other nonpositional goods”. American Economic Review, 75(1): 101–16.
Frank, R. (2005) “Positional externalities cause large and preventable welfare losses”. American Economic Review, 95(2): 137–141.
Frey, B., and Stutzer, A. (2002) “What can economists learn from happiness research?”. Journal of Economic Literature, 40(2): 402–435.
Hirsch, F. (1977) Social Limits to Growth. Routledge and Kegan Paul Ltd., London.
Hoel, M., and Sterner, T. (2007) “Discounting and relative prices”. Climatic Change, 84: 265–280.
Howarth, R. (2000) “Climate change and the representative agent”. Environmental and Resource Economics, 15(2): 135–148.
Intergovernmental Panel on Climate Change (1996) “Climate Change 1995: Economic and Social Dimensions of Climate Change”. Contribution of Working Group III to the Second Assessment Report of the Intergovernmental Panel on Climate Change.
Johansson-Stenman, O., Carlson, F., and Daruvala, D. (2002) “Measuring future grandparents’ preferences for equality and relative standing”. Economic Journal, 112(479): 362–383.
Luttmer, E. (2005) “Neighbors as negatives: relative earnings and well-being”. The Quarterly Journal of Economics, 120(3): 963–1002.
Mantel, R. (1976) “Homothetic preferences and community excess demand functions”. Journal of Economic Theory, 12(2): 197–201.
Michl, T. (2010) “Discounting Nordhaus”. Review of Political Economy, 22(4): 535–549.
Mitchell, R., and Carson, R. (1989) Using Surveys to Value Public Goods: The Contingent Valuation Method. Resources for the Future, Washington D.C.
Ng, Y., and Wang, J. (1995) “A case for cardinal utility and non-arbitrary choice of commodity units”. Social Choice and Welfare, 12(3): 255–266.
Nordhaus, W.D. (2006a) “Principles of National Accounting for Nonmarket Accounts”. In A New Architecture for the U.S. National Accounts, D. Jorgenson, J. Landefeld and W.D. Nordhaus, eds., University of Chicago Press, Chicago.
Nordhaus, W.D. (2006b) “The ‘Stern Review’ on the economics of climate change”. NBER Working Paper 12741, http://www.nber.org/papers/w12741
Nordhaus, W.D. (2008) A Question of Balance: Weighing the Options on Global Warming. Yale University Press, New Haven.
Nordhaus, W.D., and Boyer, J. (2000) Warming the World: Economic Models of Global Warming. MIT Press, Cambridge.
Rezai, A., Foley, D., and Taylor, L. (2011) “Global Warming and Economic Externalities”. Economic Theory, 49(2): 329–351.
Sen, A. (1982) “Approaches to the choice of discount rates for social benefit-cost analysis”. In Discounting for Time and Risk in Energy Policy, R.C. Lind et al., eds., pp. 325–353, Resources for the Future, Washington D.C.
Sen, A. (1983) “Poor, relatively speaking”. Oxford Economic Papers, 35(2): 153–169.
Skott, P., and Davis, L. (2012) “Distributional biases in the evaluation of climate change”. Ecological Economics, doi: 10.1016/j.ecolecon.2012.06.014.
Sonnenschein, H. (1972) “Market excess demand functions”. Econometrica, 40(3): 549–563.
Stern, N. (2007) The Economics of Climate Change: The Stern Review. Cambridge University Press, Cambridge. Online at http://www.hm-treasury.gov.uk/independent_reviews/stern_review_climate_change/sternreview_index.cfm.
Tversky, A., and Kahneman, D. (1991) “Loss aversion in riskless choice: a reference-dependent model”. The Quarterly Journal of Economics, 106(4): 1039–1061.
Veblen, T. (1899) The Theory of the Leisure Class: An Economic Study of Institutions. The Macmillan Company, New York.
Venkatachalam, L. (2004) “The contingent valuation method: a review”. Environmental Impact Assessment Review, 24(1): 89–124.
Weitzman, M.L. (2007) “A review of ‘The Stern Review on the Economics of Climate Change’”. Journal of Economic Literature, 45(3): 703–724.
Weitzman, M.L. (2009) “On modeling and interpreting the economics of catastrophic climate Change”. Review of Economics and Statistics, 91(1): 1–19.
Woodford, M. (2003) Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton University Press, Princeton.
QUESTION 1:
Global warming and other environmental changes threaten the survival of some animal species. According to some studies as many as 25 per cent of all species may become extinct before 2100 under current trends. Policy intervention may change this scenario and ensure the survival of the endangered species.
How large a proportion of your stream of current and future income would you be willing to give up in order to ensure that no existing species become extinct?
_____ 0–5%
_____ 5–10%
_____ 10–20%
_____ more than 20%
QUESTION 2:
Global warming and other environmental changes threaten the survival of some animal species. According to some studies as many as 25 per cent of all species may become extinct before 2100 under current trends. Policy intervention may change this scenario and ensure the survival of the endangered species.
Suppose that the costs of the intervention are shared and that all incomes are reduced by the same percentage. In your view, how large a proportion of current and future incomes should we be willing to give up in order to ensure that no existing species become extinct?
_____ 0–5%
_____ 5–10%
_____ 10–20%
_____ more than 20%
QUESTION 3:
Global warming and other environmental changes threaten the survival of some animal species. According to some studies as many as 25 per cent of all species may become extinct before 2100 under current trends. Policy intervention may change this scenario and ensure the survival of the endangered species.
Suppose that the intervention is financed by reducing the growth rate of the average income and that this reduction is the same for everyone. As an example, if the intervention requires reducing the growth rate of average income from 2% a year to 1.5%, then everyone will experience income growth that is 0.5 percentage points lower than without intervention. In your view, how large a reduction of the growth rate of future incomes should we be willing to accept to ensure that no existing species become extinct?
_____ 0 percentage points
_____ 0–0.1 percentage points
_____ 0.1–0.3 percentage points
_____ 0.3–1 percentage points
_____ more than 1 percentage point
Table 6.1 Survey results
| Level reductions | g − ρ = −1% | g − ρ = −2% | g − ρ = −3% | g − ρ = −4% |
| 0% | 0% growth reduction | 0% growth reduction | 0% growth reduction | 0% growth reduction |
| 0–5% | 0–0.05% growth reduction | 0–0.11% growth reduction | 0–0.16% growth reduction | 0–0.21% growth reduction |
| 5–10% | 0.05–0.11% growth reduction | 0.11–0.22% growth reduction | 0.16–0.33% growth reduction | 0–0.44% growth reduction |
| 10–20% | 0.11–0.25% growth reduction | 0.22–0.5% growth reduction | 0.33–0.75% growth reduction | 0.44–1% growth reduction |
| More than 20% | more than 0.25% growth reduction | more than 0.5% growth reduction | more than 0.75% growth reduction | more than 1% growth reduction |
