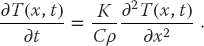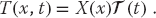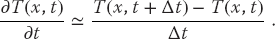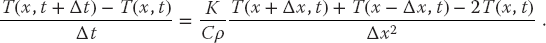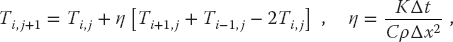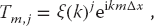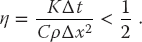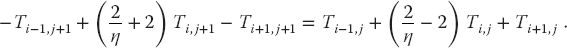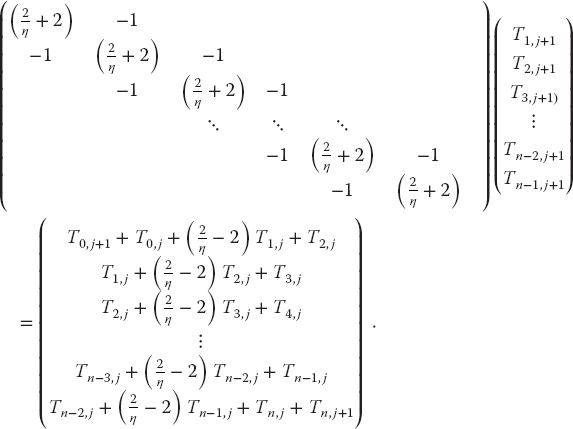20
Heat Flow via Time Stepping

---

As the present now     And the first one now

Will later be past         Will later be last

The order is                 For the times they are a-changin’.

Rapidly fadin’

Bob Dylan

This chapter examines the heat equation and develops the leapfrog method for solving it on a space–time lattice. We also develop an improved Crank–Nicolson method that determines the solution over all of space in a single step. Time stepping is simple, yet important, and we will see it again when we attack various wave equations.

20.1 Heat Flow via Time-Stepping (Leapfrog)

Problem You are given an aluminum bar of length L = 1 m and width w aligned along the x-axis (Figure 20.1). It is insulated along its length but not at its ends. Initially the bar is at a uniform temperature of 100 °C, and then both ends are placed in contact with ice water at 0°C. Heat flows out of the noninsulated ends only. Your problem is to determine how the temperature will vary as we move along the length of the bar at later times.

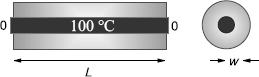
Figure 20.1 A metallic bar insulated along its length with its ends in contact with ice. The bar is displayed in dark gray and the insulation is of lighter gray.

20.2 The Parabolic Heat Equation (Theory)

A basic fact of nature is that heat flows from hot to cold, that is, from regions of high temperature to regions of low temperature. We give these words mathematical expression by stating that the rate of heat flow H through a material is proportional to the gradient of the temperature T across the material:

(20.1)

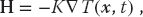
where K is the thermal conductivity of the material. The total amount of heat Q(t) in the material at any one time is proportional to the integral of the temperature over the material’s volume:

(20.2)

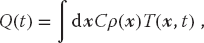
where C is the specific heat of the material and ρ is its density. Because energy is conserved, the rate of decrease in Q with time must equal the amount of heat flowing out of the material. After this energy balance is struck and the divergence theorem applied, there results the heat equation

(20.3)

The heat equation (20.3) is a parabolic PDE with space and time as independent variables. The specification of this problem implies that there is no temperature variation in directions perpendicular to the bar (y and z), and so we have only one spatial coordinate in the Laplacian:

(20.4)

As given, the initial temperature of the bar and the boundary conditions are

(20.5)

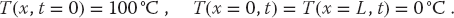
20.2.1 Solution: Analytic Expansion

Analogous to Laplace’s equation, the analytic solution starts with the assumption that the solution separates into the product of functions of space and time:

(20.6)

When (20.6) is substituted into the heat equation (20.4) and the resulting equation is divided by X(x)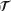(t), two noncoupled ODEs result:

(20.7)

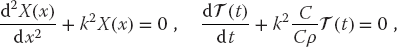
where k is a constant still to be determined. The boundary condition that the temperature equals zero at x = 0 requires a sine function for X:

(20.8)

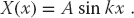
The boundary condition that the temperature equals zero at x = L requires the sine function to vanish there:

(20.9)

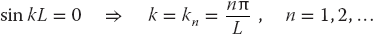
To avoid blow up, the time function must be a decaying exponential with k in the exponent:

(20.10)

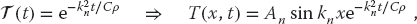
where n can be any integer and A_n is an arbitrary constant. Because (20.4) is a linear equation, the most general solution is a linear superposition of X_n(x)T_n(t) products for all values of n:

(20.11)

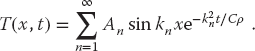
The coefficients A_n are determined by the initial condition that at time t = 0 the entire bar has temperature T = 100 K:

(20.12)

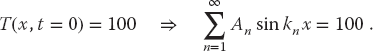
Projecting the sine functions determines A_n = 4T₀/nπ for n odd, and so

(20.13)

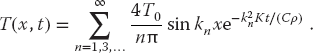
20.2.2 Solution: Time Stepping

As we did with Laplace’s equation, the numerical solution is based on converting the differential equation to a finite-difference (“difference”) equation. We discretize space and time on a lattice (Figure 20.2) and solve for solutions on the lattice sites. The sites along the top with white centers correspond to the known values of the temperature for the initial time, while the sites with white centers along the sides correspond to the fixed temperature along the boundaries. If we also knew the temperature for times along the bottom row, then we could use a relaxation algorithm as we did for Laplace’s equation. However, with only the top and side rows known, we shall end up with an algorithm that steps forward in time one row at a time, as in the children’s game leapfrog.

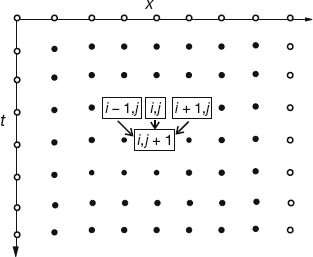
Figure 20.2 The algorithm for the heat equation in which the temperature at the location x = iΔx and time t = (j + 1)Δt is computed from the temperature values at three points of an earlier time. The nodes with white centers correspond to known initial and boundary conditions (the boundaries are placed artificially close for illustrative purposes).

As is often the case with PDEs, the algorithm is customized for the equation being solved and for the constraints imposed by the particular set of initial and boundary conditions. With only one row of times to start with, we use a forward-difference approximation for the time derivative of the temperature:

(20.14)

Because we know the spatial variation of the temperature along the entire top row and the left and right sides, we are less constrained with the space derivative as with the time derivative. Consequently, as we did with the Laplace equation, we use the more accurate central-difference approximation for the space derivative:

(20.15)

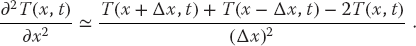
Substitution of these approximations into (20.4) yields the heat difference equation

(20.16)

We reorder (20.16) into a form in which T can be stepped forward in t:

(20.17)

where x = iΔx and t = jΔt. This algorithm is explicit because it provides a solution in terms of known values of the temperature. If we tried to solve for the temperature at all lattice sites in Figure 20.2 simultaneously, then we would have an implicit algorithm that requires us to solve equations involving unknown values of the temperature. We see that the temperature at space–time point (i, j + 1) is computed from the three temperature values at an earlier time j and at adjacent space values i ± 1, i. We start the solution at the top row, moving it forward in time for as long as we want and keeping the temperature along the ends fixed at 0 K (Figure 20.2).

20.2.3 von Neumann Stability Assessment

When we solve a PDE by converting it to a difference equation, we hope that the solution of the latter is a good approximation to the solution of the former. If the difference-equation solution diverges, then we know we have a bad approximation, but if it converges, then we may feel confident that we have a good approximation to the PDE. The von Neumann stability analysis is based on the assumption that eigenmodes of the difference equation can be expressed as

(20.18)

where x = mΔx and t = jΔt, and 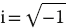is the imaginary number. The constant k in (20.18) is an unknown wave vector (2π/λ), and (k) is an unknown complex function. View (20.18) as a basis function that oscillates in space (the exponential) with an amplitude or amplification factor (k)^j that increases by a power of for each time step. If the general solution to the difference equation can be expanded in terms of these eigenmodes, then the general solution will be stable if the eigenmodes are stable. Clearly, for an eigenmode to be stable, the amplitude cannot grow in time j, which means |(k)| < 1 for all values of the parameter k (Press et al., 1994; Ancona, 2002).

Application of a stability analysis is more straightforward than it might appear. We just substitute expression (20.18) into the difference equation (20.17):

(20.19)

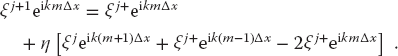
After canceling some common factors, it is easy to solve for :

(20.20)

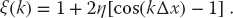
In order for |(k)| < 1 for all possible k values, we must have

(20.21)

This equation tells us that if we make the time step Δt smaller, we will always improve the stability, as we would expect. But if we decrease the space step Δx without a simultaneous quadratic increase in the time step, we will worsen the stability. The lack of space–time symmetry arises from our use of stepping in time, but not in space.

In general, you should perform a stability analysis for every PDE you have to solve, although it can get complicated (Press et al., 1994). Yet even if you do not, the lesson here is that you may have to try different combinations of Δx and Δt variations until a stable, reasonable solution is obtained. You may expect, nonetheless, that there are choices for Δx and Δt for which the numerical solution fails and that simply decreasing an individual Δx or Δt, in the hope that this will increase precision, may not improve the solution.

Listing 20.1 EqHeat.py solves the 1D space heat equation on a lattice by leapfrogging (time-stepping) the initial conditions forward in time. You will need to adjust the parameters to obtain a solution like those in the figures.

20.2.4 Heat Equation Implementation

Recall that we want to solve for the temperature distribution within an aluminum bar of length L = 1 m subject to the boundary and initial conditions

(20.22)

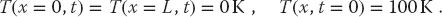
The thermal conductivity, specific heat, and density for Al are

(20.23)

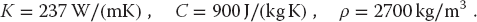
1. Write or modify EqHeat.py in Listing 20.1 to solve the heat equation.
2. Define a 2D array T[101,2] for the temperature as a function of space and time. The first index is for the 100 space divisions of the bar, and the second index is for present and past times (because you may have to make thousands of time steps, you save memory by saving only two times).
3. For time t = 0 (j = 1), initialize T so that all points on the bar except the ends are at 100 K. Set the temperatures of the ends to 0 K.
4. Apply (20.14) to obtain the temperature at the next time step.
5. Assign the present-time values of the temperature to the past values: T[i,1] = T[i,2], i = 1,…,101.
6. Start with 50 time steps. Once you are confident the program is running properly, use thousands of steps to see the bar cool smoothly with time. For approximately every 500 time steps, print the time and temperature along the bar.

20.3 Assessment and Visualization

1. Check that your program gives a temperature distribution that varies smoothly along the bar and agrees with the boundary conditions, as in Figure 20.3.

   

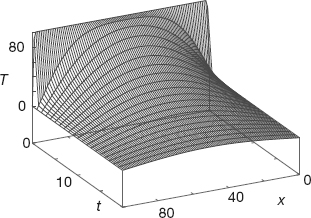
   Figure 20.3 A numerical calculation of the temperature vs. position and vs. time, with isotherm contours projected onto the horizontal plane.

2. Check that your program gives a temperature distribution that varies smoothly with time and reaches equilibrium. You may have to vary the time and space steps to obtain stable solutions.
3. Compare the analytic and numeric solutions (and the wall times needed to compute them). If the solutions differ, suspect the one that does not appear smooth and continuous.
4. Make a surface plot of temperature vs. position vs. time.
5. Plot the isotherms (contours of constant temperature).
6. Stability test: Verify the stability condition (20.21) by observing how the temperature distribution diverges if η > 1/4.
7. Material dependence: Repeat the calculation for iron. Note that the stability condition requires you to change the size of the time step.
8. Initial sinusoidal distribution sin(πx/L): Compare to the analytic solution,
   (20.24)
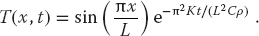
9. Two bars in contact: Two identical bars 0.25 m long are placed in contact along one of their ends with their other ends kept at 0 K. One is kept in a heat bath at 100 K, and the other at 50 K. Determine how the temperature varies with time and location (Figure 20.4).
10. Radiating bar (Newton’s cooling): Imagine now that instead of being insulated along its length, a bar is in contact with an environment at a temperature T_e. Newton’s law of cooling (radiation) says that the rate of temperature change as a result of radiation is
    (20.25)

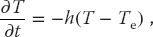
    where h is a positive constant. This leads to the modified heat equation

    (20.26)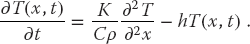

    Modify the algorithm to include Newton’s cooling and compare the cooling of a radiating bar with that of the insulated bar.

20.4 Improved Heat Flow: Crank–Nicolson Method

The Crank–Nicolson method (Crank and Nicolson, 1946) provides a higher degree of precision for the heat equation (20.3) than the simple leapfrog method we have just discussed. This method calculates the time derivative with a central-difference approximation, in contrast to the forward-difference approximation used previously. In order to avoid introducing error for the initial time step where only a single time value is known, the method uses a split time step,¹⁾ so that time is advanced from time t to t + Δt/2:

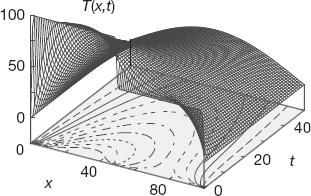
Figure 20.4 Temperature vs. position and time when two bars at differing temperatures are placed in contact at t = 0. The projected contours show the isotherms.

(20.27)

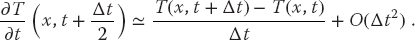
Yes, we know that this looks just like the forward-difference approximation for the derivative at time t + Δt, for which it would be a bad approximation; regardless, it is a better approximation for the derivative at time t + Δt/2, although it makes the computation more complicated. Likewise, in (20.14) we gave the central-difference approximation for the second space derivative for time t. For t = t + Δt/2, that becomes

(20.28)

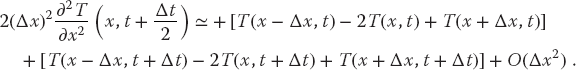
In terms of these expressions, the heat difference equation is

(20.29)

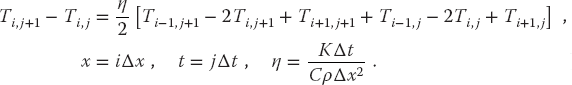
We group together terms involving the same temperature to obtain an equation with future times on the LHS and present times on the RHS:

(20.30)

This equation represents an implicit scheme for the temperature T_i,j, where the word “implicit” means that we must solve simultaneous equations to obtain the full solution for all space. In contrast, an explicit scheme requires iteration to arrive at the solution. It is possible to solve (20.30) simultaneously for all unknown temperatures (1 ≤ i ≤ N) at times j and j + 1. We start with the initial temperature distribution throughout all of space, the boundary conditions at the ends of the bar for all times, and the approximate values from the first derivative:

(20.31)

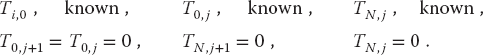
We rearrange (20.30) so that we can use these known values of T to step the j = 0 solution forward in time by expressing (20.30) as a set of simultaneous linear equations (in the matrix form):

(20.32)

Observe that the Ts on the RHS are all at the present time j for various positions, and at future time j + 1 for the two ends (whose Ts are known for all times via the boundary conditions). We start the algorithm with the T_i,j=0 values of the initial conditions, then solve a matrix equation to obtain T_i,j=1. With that we know all the terms on the RHS of the equations (j = 1 throughout the bar and j = 2 at the ends) and so can repeat the solution of the matrix equations to obtain the temperature throughout the bar for j = 2. So again, we time-step forward, only now we solve matrix equations at each step. That gives us the spatial solution at all locations directly.

Not only is the Crank–Nicolson method more precise than the low-order time-stepping method, but it also is stable for all values of Δt and Δx. To prove that, we apply the von Neumann stability analysis discussed in Section 20.2.3 to the Crank–Nicolson algorithm by substituting (20.17) into (20.30). This determines an amplification factor

(20.33)

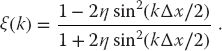
Because sin²() is positive definite, this proves that || ≤ 1 for all Δt, Δx, and k.

20.4.1 Solution of Tridiagonal Matrix Equations

The Crank–Nicolson equations (20.32) are in the standard [A]x = b form for linear equations, and so we can use our previous methods to solve them. Nonetheless, because the coefficient matrix [A] is tridiagonal (zero elements except for the main diagonal and two diagonals on either side of it),

(20.34)

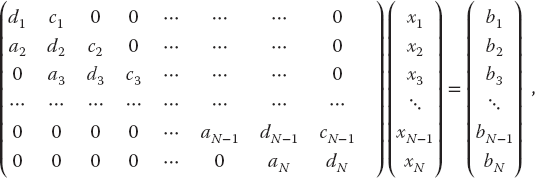
a more robust and faster solution exists that makes this implicit method as fast as an explicit one. Because tridiagonal systems occur frequently, we now outline the specialized technique for solving them (Press et al., 1994). If we store the matrix elements a_i,j using both subscripts, then we will need N² locations for elements and N² operations to access them. However, for a tridiagonal matrix, we need to store only the vectors {d_i}_i=1,N, {c_i}_i=1,N, and {a_i}_i=1,N, along, above, and below the diagonals. The single subscripts on a_i, d_i, and c_i reduce the processing from N² to (3N − 2) elements.

We solve the matrix equation by manipulating the individual equations until the coefficient matrix is upper triangular with all the elements of the main diagonal equal to 1. We start by dividing the first equation by d₁, then subtract a₂ times the first equation,

(20.35)

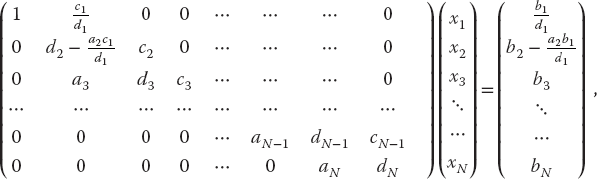
and then dividing the second equation by the second diagonal element,

(20.36)

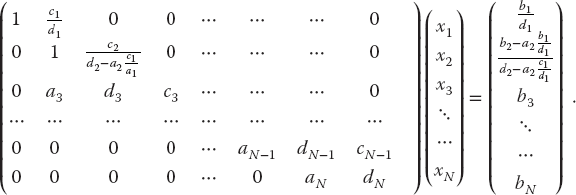
Assuming that we can repeat these steps without ever dividing by zero, the system of equations will be reduced to upper triangular form,

(20.37)

where h₁ = c₁/d₁ and p₁ = b₁/d₁. We then recur for the others elements:

(20.38)

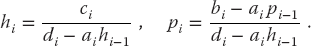
Finally, back substitution leads to the explicit solution for the unknowns:

(20.39)

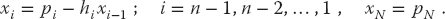
In Listing 20.2, we give the program HeatCNTridiag.py that solves the heat equation using the Crank–Nicolson algorithm via a triadiagonal reduction.

Listing 20.2 HeatCNTridiag.py is the complete program for solution of the heat equation in one space dimension and time via the Crank–Nicolson method. The resulting matrix equations are solved via a technique specialized to tridiagonal matrices.

20.4.2 Crank–Nicolson Implementation, Assessment

1. Write a program using the Crank–Nicolson method to solve for the heat flow in the metal bar of Section 20.1 for at least 100 time steps.
2. Solve the linear system of equations (20.32) using either Matplotlib or the special tridiagonal algorithm.
3. Check the stability of your solution by choosing different values for the time and space steps.
4. Construct a contoured surface plot of temperature vs. position and vs. time.
5. Compare the implicit and explicit algorithms used in this chapter for relative precision and speed. You may assume that a stable answer that uses very small time steps is accurate.

1) In Section 22.2.1 we develop a different split-time algorithm for the solution of the Schrödinger equation. There the real and imaginary parts of the wave function are computed at times that differ by Δt/2.