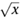 . Similarly, x1/3 =
. Similarly, x1/3 = 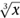 , the cube root. Continuing in this manner we can define xp/q for any fraction p/q. Then, using fractions to approximate real numbers, we can define xa for any real a. And the equation xaxb = xa+b still holds.
, the cube root. Continuing in this manner we can define xp/q for any fraction p/q. Then, using fractions to approximate real numbers, we can define xa for any real a. And the equation xaxb = xa+b still holds.Along with numbers came arithmetic: methods for adding, subtracting, multiplying, and dividing numbers. Devices like the abacus were used to do the sums; then the results could be recorded in symbols. After a time, ways were found to use the symbols to perform the calculations without mechanical assistance, although the abacus is still widely used in many parts of the world, while electronic calculators have supplanted pen and paper calculations in most other countries.
Arithmetic proved essential in other ways, too, especially in astronomy and surveying. As the basic outlines of the physical sciences began to emerge, the fledgeling scientists needed to perform ever more elaborate calculations, by hand. Often this took up much of their time, sometimes months or years, getting in the way of more creative activities. Eventually it became essential to speed up the process. Innumerable mechanical devices were invented, but the most important breakthrough was a conceptual one: think first, calculate later. Using clever mathematics, you could make difficult calculations much easier.
The new mathematics quickly developed a life of its own, turning out to have deep theoretical implications as well as practical ones. Today, those early ideas have become an indispensable tool throughout science, reaching even into psychology and the humanities. They were widely used until the 1980s, when computers rendered them obsolete for practical purposes, but, despite that, their importance in mathematics and science has continued to grow.
The central idea is a mathematical technique called a logarithm. Its inventor was a Scottish laird, but it took a geometry professor with strong interests in navigation and astronomy to replace the laird’s brilliant but flawed idea by a much better one.
In March 1615 Henry Briggs wrote a letter to James Ussher, recording a crucial event in the history of science:
Napper, lord of Markinston, hath set my head and hands a work with his new and admirable logarithms. I hope to see him this summer, if it please God, for I never saw a book which pleased me better or made me more wonder.
Briggs was the first professor of geometry at Gresham College in London, and ‘Napper, lord of Markinston’ was John Napier, eighth laird of Merchiston, now part of the city of Edinburgh in Scotland. Napier seems to have been a bit of a mystic; he had strong theological interests, but they mostly centred on the book of Revelation. In his view, his most important work was A Plaine Discovery of the Whole Revelation of St John, which led him to predict that the world would end in either 1688 or 1700. He is thought to have engaged in both alchemy and necromancy, and his interests in the occult lent him a reputation as a magician. According to rumour, he carried a black spider in a small box everywhere he went, and possessed a ‘familiar’, or magical companion: a black cockerel. According to one of his descendants, Mark Napier, John employed his familiar to catch servants who were stealing. He locked the suspect in a room with the cockerel and instructed them to stroke it, telling them that his magical bird would unerringly detect the guilty. But Napier’s mysticism had a rational core, which in this particular instance involved coating the cockerel with a thin layer of soot. An innocent servant would be confident enough to stroke the bird as instructed, and would get soot on their hands. A guilty one, fearing detection, would avoid stroking the bird. So, ironically, clean hands proved you were guilty.
Napier devoted much of his time to mathematics, especially methods for speeding up complicated arithmetical calculations. One invention, Napier’s bones, was a set of ten rods, marked with numbers, which simplified the process of long multiplication. Even better was the invention that made his reputation and created a scientific revolution: not his book on Revelation, as he had hoped, but his Mirifici Logarithmorum Canonis Descriptio (‘Description of the Wonderful Canon of Logarithms’) of 1614. The preface shows that Napier knew exactly what he had produced, and what it was good for.1
Since nothing is more tedious, fellow mathematicians, in the practice of the mathematical arts, than the great delays suffered in the tedium of lengthy multiplications and divisions, the finding of ratios, and in the extraction of square and cube roots – and . . . the many slippery errors that can arise: I had therefore been turning over in my mind, by what sure and expeditious art, I might be able to improve upon these said difficulties. In the end after much thought, finally I have found an amazing way of shortening the proceedings . . . it is a pleasant task to set out the method for the public use of mathematicians.
The moment Briggs heard of logarithms, he was enchanted. Like many mathematicians of his era, he spent a lot of his time performing astronomical calculations. We know this because another letter from Briggs to Ussher, dated 1610, mentions calculating eclipses, and because Briggs had earlier published two books of numerical tables, one related to the North Pole and the other to navigation. All of these works had required vast quantities of complicated arithmetic and trigonometry. Napier’s invention would save a great deal of tedious labour. But the more Briggs studied the book, the more convinced he became that although Napier’s strategy was wonderful, he’d got his tactics wrong. Briggs came up with a simple but effective improvement, and made the long journey to Scotland. When they met, ‘almost one quarter of an hour was spent, each beholding the other with admiration, before one word was spoken’.2
What was it that excited so much admiration? The vital observation, obvious to anyone learning arithmetic, was that adding numbers is relatively easy, but multiplying them is not. Multiplication requires many more arithmetical operations than addition. For example, adding two ten-digit numbers involves about ten simple steps, but multiplication requires 200. With modern computers, this issue is still important, but now it is tucked away behind the scenes in the algorithms used for multiplication. But in Napier’s day it all had to be done by hand. Wouldn’t it be great if there were some mathematical trick that would convert those nasty multiplications into nice, quick addition sums? It sounds too good to be true, but Napier realised that it was possible. The trick was to work with powers of a fixed number.
In algebra, powers of an unknown x are indicated by a small raised number. That is, xx = x2, xxx = x3, xxxx = x4, and so on, where as usual in algebra placing two letters next to each other means you should multiply them together. So, for instance, 104 = 10 × 10 × 10 × 10 = 10,000. You don’t need to play around with such expressions for long before you discover an easy way to work out, say, 104 × 103. Just write down
10,000 × 1,000 = (10 × 10 × 10 × 10) × (10 × 10 × 10)
= 10 × 10 × 10 × 10 × 10 × 10 × 10
= 10,000,000
The number of 0s in the answer is 7, which equals 4 + 3. The first step in the calculation shows why it is 4 + 3: we stick four 10s and three 10s next to each other. In short,
104 × 103 = 104+3 = 107
In the same way, whatever the value of x might be, if we multiply its ath power by its bth power, where a and b are whole numbers, then we get the (a + b)th power:
xa xb = xa+b
This may seem an innocuous formula, but on the left it multiplies two quantities together, while on the right the main step is to add a and b, which is simpler.
Suppose you wanted to multiply, say, 2.67 by 3.51. By long multiplication you get 9.3717, which to two decimal places is 9.37. What if you try to use the previous formula? The trick lies in the choice of x. If we take x to be 1.001, then a bit of arithmetic reveals that
(1.001)983 = 2.67
(1.001)1256 = 3.51
correct to two decimal places. The formula then tells us that 2.87 × 3.41 is
(1.001)983+1256 = (1.001)2239
which, to two decimal places, is 9.37.
The core of the calculation is an easy addition: 983 + 1256 = 2239. However, if you try to check my arithmetic you will quickly realise that if anything I’ve made the problem harder, not easier. To work out (1.001)983 you have to multiply 1.001 by itself 983 times. And to discover that 983 is the right power to use, you have to do even more work. So at first sight this seems like a pretty useless idea.
Napier’s great insight was that this objection is wrong. But to overcome it, some hardy soul has to calculate lots of powers of 1.001, starting with (1.001)2 and going up to something like (1.001)10,000. Then they can publish a table of all these powers. After that, most of the work has been done. You just have to run your fingers down the successive powers until you see 2.67 next to 983; you similarly locate 3.51 next to 1256. Then you add those two numbers to get 2239. The corresponding row of the table tells you that this power of 1.001 is 9.37. Job done.
Really accurate results require powers of something a lot closer to 1, such as 1.000001. This makes the table far bigger, with a million or so powers. Doing the calculations for that table is a huge enterprise. But it has to be done only once. If some self-sacrificing benefactor makes the effort up front, succeeding generations will be saved a gigantic amount of arithmetic.
In the context of this example, we can say that the powers 983 and 1256 are the logarithms of the numbers 2.67 and 3.51 that we wish to multiply. Similarly 2239 is the logarithm of their product 9.38. Writing log as an abbreviation, what we have done amounts to the equation
log ab = log a + log b
which is valid for any numbers a and b. The rather arbitrary choice of 1.001 is called the base. If we use a different base, the logarithms that we calculate are also different, but for any fixed base everything works the same way.
This is what Napier should have done. But for reasons that we can only guess at, he did something slightly different. Briggs, approaching the technique from a fresh perspective, spotted two ways to improve on Napier’s idea.
When Napier started thinking about powers of numbers, in the late sixteenth century, the idea of reducing multiplication to addition was already circulating among mathematicians. A rather complicated method known as ‘prosthapheiresis’, based on a formula involving trigonometric functions, was in use in Denmark.3 Napier, intrigued, was smart enough to realise that powers of a fixed number could do the same job more simply. The necessary tables didn’t exist – but that was easily remedied. Some public-spirited soul must carry out the work. Napier volunteered himself for the task, but he made a strategic error. Instead of using a base that was slightly bigger than 1, he used a base slightly smaller than 1. In consequence, the sequence of powers started out with big numbers, which got successively smaller. This made the calculations slightly more clumsy.
Briggs spotted this problem, and saw how to deal with it: use a base slightly larger than 1. He also spotted a subtler problem, and dealt with that as well. If Napier’s method were modified to work with powers of something like 1.0000000001, there would be no straightforward relation between the logarithms of, say, 12.3456 and 1.23456. So it wasn’t entirely clear when the table could stop. The source of the problem was the value of log 10, because
log 10x = log 10 + log x
Unfortunately log 10 was messy: with the base 1.0000000001 the logarithm of 10 was 23,025,850,929. Briggs thought it would be much nicer if the base could be chosen so that log 10 = 1. Then log 10x = 1 + log x, so that whatever log 1.23456 might be, you just had to add 1 to it to get log 12.3456. Now tables of logarithms need only run from 1 to 10. If bigger numbers turned up, you just added the appropriate whole number.
To make log 10 = 1, you do what Napier did, using a base of 1.0000000001, but then you divide every logarithm by that curious number 23,025,850,929. The resulting table consists of logarithms to base 10, which I’ll write as log10 x. They satisfy
log10 xy = log10x + log10y
as before, but also
log10 10x = log10x + 1
Within two years Napier was dead, so Briggs started work on a table of base-10 logarithms. In 1617 he published Logarithmorum Chilias Prima (‘Logarithms of the First Chiliad’), the logarithms of the integers from 1 to 1000 accurate to 14 decimal places. In 1624 he followed it up with Arithmetic Logarithmica (‘Arithmetic of Logarithms’), a table of base-10 logarithms of numbers from 1 to 20,000 and from 90,000 to 100,000, to the same accuracy. Others rapidly followed Briggs’s lead, filling in the large gap and developing auxiliary tables such as logarithms of trigonometric functions like log sin x.
The same ideas that inspired logarithms allow us to define powers xa of a positive variable x for values of a that are not positive whole numbers. All we have to do is insist that our definitions must be consistent with the equation xaxb = xa+b, and follow our noses. To avoid nasty complications, it is best to assume x is positive, and to define xa so that this is also positive. (For negative x, it’s best to introduce complex numbers, as in Chapter 5.)
For example, what is x0? Bearing in mind that x1 = x, the formula says that x0 must satisfy x0x = x0+1 = x. Dividing by x we find that x = 1. Now what about x−1? Well, the formula says that x−1x = x−1+1 = x0 = 1. Dividing by x, we get x−1 = 1/x. Similarly x−2 = 1/x2, x−3 = 1/x3, and so on.
It starts to get more interesting, and potentially very useful, when we think about x1/2. This has to satisfy x1/2 x1/2 = x1/2+1/2 = x1 = x. So x1/2, multiplied by itself, is x. The only number with this property is the square root of x. So x1/2 = 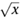 . Similarly, x1/3 =
. Similarly, x1/3 = 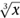 , the cube root. Continuing in this manner we can define xp/q for any fraction p/q. Then, using fractions to approximate real numbers, we can define xa for any real a. And the equation xaxb = xa+b still holds.
, the cube root. Continuing in this manner we can define xp/q for any fraction p/q. Then, using fractions to approximate real numbers, we can define xa for any real a. And the equation xaxb = xa+b still holds.
It also follows that log 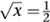 log x, and log
log x, and log 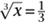 log x, so we can calculate square roots and cube roots easily using a table of logarithms. For example, to find the square root of a number we form its logarithm, divide by 2, and then work out which number has the result as its logarithm. For cube roots, do the same but divide by 3. Traditional methods for these problems were tedious and complicated. You can see why Napier showcased square and cube roots in the preface to his book.
log x, so we can calculate square roots and cube roots easily using a table of logarithms. For example, to find the square root of a number we form its logarithm, divide by 2, and then work out which number has the result as its logarithm. For cube roots, do the same but divide by 3. Traditional methods for these problems were tedious and complicated. You can see why Napier showcased square and cube roots in the preface to his book.
As soon as complete tables of logarithms were available, they became an indispensable tool for scientists, engineers, surveyors, and navigators. They saved time, they saved effort, and they increased the likelihood that the answer was correct. Early on, astronomy was a major beneficiary, because astronomers routinely needed to perform long and difficult calculations. The French mathematician and astronomer Pierre Simon de Laplace said that the invention of logarithms ‘reduces to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust’. As the use of machinery in manufacturing grew, engineers started to make more and more use of mathematics – to design complex gears, analyse the stability of bridges and buildings, and construct cars, lorries, ships, and aeroplanes. Logarithms were a firm part of the school mathematics curriculum a few decades ago. And engineers carried what was in effect an analogue calculator for logarithms in their pockets, a physical representation of the basic equation for logarithms for on-the-spot use. They called it a slide rule, and they used it routinely in applications ranging from architecture to aircraft design.
The first slide rule was constructed by an English mathematician, William Oughtred, in 1630, using circular scales. He modified the design in 1632, by making the two rulers straight. This was the first slide rule. The idea is simple: when you place two rods end to end, their lengths add. If the rods are marked using a logarithmic scale, in which numbers are spaced according to their logarithms, then the corresponding numbers multiply. For instance, set the 1 on one rod against the 2 on the other. Then against any number x on the first rod, we find 2x on the second. So opposite 3 we find 6, and so on, see Figure 11. If the numbers are more complicated, say 2.67 and 3.51, we place 1 opposite 2.67 and read off whatever is opposite 3.59, namely 9.37. It’s just as easy.
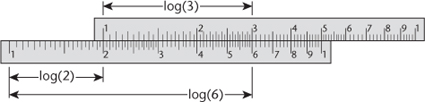
Fig 11 Multiplying 2 by 3 on a slide rule.
Engineers quickly developed fancy slide rules with trigonometric functions, square roots, log-log scales (logarithms of logarithms) to calculate powers, and so on. Eventually logarithms took a back seat to digital computers, but even now the logarithm still plays a huge role in science and technology, alongside its inseparable companion, the exponential function. For base-10 logarithms, this is the function 10x; for natural logarithms, the function ex, where e = 2.71828, approximately. In each pair, the two functions are inverse to each other. If you take a number, form its logarithm, and then form the exponential of that, you get back the number you started with.
Why do we need logarithms now that we have computers?
In 2011 a magnitude 9.0 earthquake just off the east coast of Japan caused a gigantic tsunami, which devastated a large populated area and killed around 25,000 people. On the coast was a nuclear power plant, Fukushima Dai-ichi (Fukushima number 1 power plant, to distinguish it from a second nuclear power plant situated nearby). It comprised six separate nuclear reactors: three were in operation when the tsunami struck; the other three had temporarily ceased operating and their fuel had been transferred to pools of water outside the reactors but inside the reactor buildings.
The tsunami overwhelmed the plant’s defences, cutting the supply of electrical power. The three operating reactors (numbers 1, 2, and 3) were shut down as a safety measure, but their cooling systems were still needed to stop the fuel from melting. However, the tsunami also wrecked the emergency generators, which were intended to power the cooling system and other safety-critical systems. The next level of backup, batteries, quickly ran out of power. The cooling system stopped and the nuclear fuel in several reactors began to overheat. Improvising, the operators used fire engines to pump seawater into the three operating reactors, but this reacted with the zirconium cladding on the fuel rods to produce hydrogen. The build-up of hydrogen caused an explosion in the building housing Reactor 1. Reactors 2 and 3 soon suffered the same fate. The water in the pool of Reactor 4 drained out, leaving its fuel exposed. By the time the operators regained some semblance of control, at least one reactor containment vessel had cracked, and radiation was leaking out into the local environment. The Japanese authorities evacuated 200,000 people from the surrounding area because the radiation was well above normal safety limits. Six months later, the company operating the reactors, TEPCO, stated that the situation remained critical and much more work would be needed before the reactors could be considered fully under control, but claimed the leakage had been stopped.
I don’t want to analyse the merits or otherwise of nuclear power here, but I do want to show how the logarithm answers a vital question: if you know how much radioactive material has been released, and of what kind, how long will it remain in the environment, where it could be hazardous?
Radioactive elements decay; that is, they turn into other elements through nuclear processes, emitting nuclear particles as they do so. It is these particles that constitute the radiation. The level of radioactivity falls away over time just as the temperature of a hot body falls when it cools: exponentially. So, in appropriate units, which I won’t discuss here, the level of radioactivity N(t) at time t follows the equation
N(t) = N0e−kt
where N0 is the initial level and k is a constant depending on the element concerned. More precisely, it depends on which form, or isotope, of the element we are considering.
A convenient measure of the time radioactivity persists is the half-life, a concept first introduced in 1907. This is the time it takes for an initial level N0 to drop to half that size. To calculate the half-life, we solve the equation
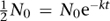
by taking logarithms of both sides. The result is
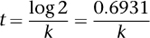
and we can work this out because k is known from experiments.
The half-life is a convenient way to assess how long the radiation will persist. Suppose that the half-life is one week, for instance. Then the original rate at which the material emits radiation halves after 1 week, is down to one quarter after 2 weeks, one eighth after 3 weeks, and so on. It takes 10 weeks to drop to one thousandth of its original level (actually 1/1024), and 20 weeks to drop to one millionth.
In accidents with conventional nuclear reactors, the most important radioactive products are iodine-131 (a radioactive isotope of iodine) and caesium-137 (a radioactive isotope of caesium). The first can cause thyroid cancer, because the thyroid gland concentrates iodine. The half-life of iodine-131 is only 8 days, so it causes little damage if the right medication is available, and its dangers decrease fairly rapidly unless it continues to leak. The standard treatment is to give people iodine tablets, which reduce the amount of the radioactive form that is taken up by the body, but the most effective remedy is to stop drinking contaminated milk.
Caesium-137 is very different: it has a half-life of 30 years. It takes about 200 years for the level of radioactivity to drop to one hundredth of its initial value, so it remains a hazard for a very long time. The main practical issue in a reactor accident is contamination of soil and buildings. Decontamination is to some extent feasible, but expensive. For example, the soil can be removed, carted away, and stored somewhere safe. But this creates huge amounts of low-level radioactive waste.
Radioactive decay is just one area of many in which Napier’s and Briggs’s logarithms continue to serve science and humanity. If you thumb through later chapters you will find them popping up in thermodynamics and information theory, for example. Even though fast computers have now made logarithms redundant for their original purpose, rapid calculations, they remain central to science for conceptual rather than computational reasons.
Another application of logarithms comes from studies of human perception: how we sense the world around us. The early pioneers of the psychophysics of perception made extensive studies of vision, hearing, and touch, and they turned up some intriguing mathematical regularities.
In the 1840s a German doctor, Ernst Weber, carried out experiments to determine how sensitive human perception is. His subjects were given weights to hold in their hands, and asked when they could tell that one weight felt heavier than another. Weber could then work out what the smallest detectable difference in weight was. Perhaps surprisingly, this difference (for a given experimental subject) was not a fixed amount. It depended on how heavy the weights being compared were. People didn’t sense an absolute minimum difference – 50 grams, say. They sensed a relative minimum difference – 1% of the weights under comparison, say. That is, the smallest difference that the human senses can detect is proportional to the stimulus, the actual physical quantity.
In the 1850s Gustav Fechner rediscovered the same law, and recast it mathematically. This led him to an equation, which he called Weber’s law, but nowadays it is usually called Fechner’s law (or the Weber–Fechner law if you’re a purist). It states that the perceived sensation is proportional to the logarithm of the stimulus. Experiments suggested that this law applies not only to our sense of weight but to vision and hearing as well. If we look at a light, the brightness that we perceive varies as the logarithm of the actual energy output. If one source is ten times as bright as another, then the difference we perceive is constant, however bright the two sources really are. The same goes for the loudness of sounds: a bang with ten times as much energy sounds a fixed amount louder.
The Weber–Fechner law is not totally accurate, but it’s a good approximation. Evolution pretty much had to come up with something like a logarithmic scale, because the external world presents our senses with stimuli over a huge range of sizes. A noise may be little more than a mouse scuttling in the hedgerow, or it may be a clap of thunder; we need to be able to hear both. But the range of sound levels is so vast that no biological sensory device can respond in proportion to the energy generated by the sound. If an ear that could hear the mouse did that, then a thunderclap would destroy it. If it tuned the sound levels down so that the thunderclap produced a comfortable signal, it wouldn’t be able to hear the mouse. The solution is to compress the energy levels into a comfortable range, and the logarithm does exactly that. Being sensitive to proportions rather than absolutes makes excellent sense, and makes for excellent senses.
Our standard unit for noise, the decibel, encapsulates the Weber–Fechner law in a definition. It measures not absolute noise, but relative noise. A mouse in the grass produces about 10 decibels. Normal conversation between people a metre apart takes place at 40–60 decibels. An electric mixer directs about 60 decibels at the person using it. The noise in a car, caused by engine and tyres, is 60–80 decibels. A jet airliner a hundred metres away produces 110–140 decibels, rising to 150 at thirty metres. A vuvuzela (the annoying plastic trumpet-like instrument widely heard during the football World Cup in 2010 and brought home as souvenirs by misguided fans) generates 120 decibels at one metre; a military stun grenade produces up to 180 decibels.
Scales like these are widely encountered because they have a safety aspect. The level at which sound can potentially cause hearing damage is about 120 decibels. Please throw away your vuvuzela.