1The Penguin Book of Curious and Interesting Mathematics by David Wells quotes a brief form of the joke: An Indian chief had three wives who were preparing to give birth, one on a buffalo hide, one on a bear hide, and the third on a hippopotamus hide. In due course, the first gave him a son, the second a daughter, and the third, twins, a boy and a girl, thereby illustrating the well-known theorem that the squaw on the hippopotamus is equal to the sum of the squaws on the other two hides. The joke goes back at least to the mid-1950s, when it was broadcast in the BBC radio series ‘My Word’, hosted by comedy scriptwriters Frank Muir and Denis Norden.
2Quoted without reference on:
http://www-history.mcs.st-and.ac.uk/HistTopics/Babylonian_Pythagoras.html
3A. Sachs, A. Goetze, and O. Neugebauer. Mathematical Cuneiform Texts, American Oriental Society, New Haven 1945.
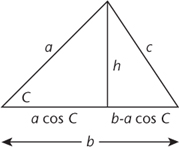
4The figure is repeated for convenience in Figure 60.
Fig 60 Splitting a triangle into two with right angles.
The perpendicular cuts the side b into two pieces. By trigonometry, one piece has length a cos C, so the other has length b-a cos C. Let h be the height of the perpendicular. By Pythagoras:
a2 = h2 + (a cos C)2
c2 = h2 + (b − a cos C)2
a2 − h2 = a2 cos2 C
c2 − h2 = (b − a cos C)2 = b2 − 2ab cos C + a2 cos2 C
Subtract the first equation from the second; now the unwanted h2 cancels out. So do the terms a2 cos2 C, and we are left with
c2 − a2 = b2 − 2ab cos C
which leads to the stated formula.
1http://www.17centurymaths.com/contents/napiercontents.html
2Quoted from a letter John Marr wrote to William Lilly.
3Prosthapheiresis was based on a trigonometric formula discovered by François Viète, namely
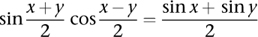
If you owned a table of sines, the formula allowed you to calculate any product using only sums, differences, and division by 2.
1Keynes never delivered the lecture. The Royal Society planned to commemorate Isaac Newton’s tercentenary in 1942, but World War II intervened, so the celebrations were postponed to 1946. The lecturers were the physicists Edward da Costa Andrade and Niels Bohr, and the mathematicians Herbert Turnbull and Jacques Hadamard. The society had also invited Keynes, whose interests included Newton’s manuscripts as well as economics. He had written a lecture with the title ‘Newton, the man’, but he died just before the event took place. His brother Geoffrey read the lecture on his behalf.
2This phrase comes from a letter that Newton wrote to Hooke in 1676. It wasn’t new: in 1159 John of Salisbury wrote that ‘Bernard of Chartres used to say that we are like dwarfs on the shoulders of giants, so that we can see more than they.’ By the seventeenth century it had become a cliché.
3Division by zero leads to fallacious proofs. For example, we can ‘prove’ that all numbers are zero. Assume that a = b. Therefore a2 = ab, so a2 − b2 = ab − b2. Factorise to get (a + b)(a − b) = b(a − b). Divide by (a − b) to deduce that a + b = b. Therefore a = 0. The error is the division by (a − b), which is 0 because we assumed a = b.
4Richard Westfall. Never at Rest, Cambridge University Press, Cambridge 1980, p. 425.
5Erik H. Hauri, Thomas Weinreich, Alberto E. Saal, Malcolm C. Rutherford, and James A. Van Orman. High pre-eruptive water contents preserved in lunar melt inclusions, Science Online (26 May 2011) 1204626. [DOI:10.1126/science. 1204626]. Their results proved controversial.
6However, it’s not coincidence. It works for any differentiable function: one with a continuous derivative. These include all polynomials and all convergent power series, such as the logarithm, the exponential, and the various trigonometric functions.
7The modern definition is: a function f(h) tends to a limit L as h tends to zero if for any ε > 0 there exists δ > 0 such that |h| < δ implies that |f(h)−L| < ε. Using any ε > 0 avoids referring to anything flowing or becoming smaller: it deals with all possible values in one go.
1The book of Genesis refers to the ‘firmament’. Most scholars think this derives from the ancient Hebrew belief that the stars were tiny lights fixed to a solid vault of Heaven, shaped like a hemisphere. This is what the night sky looks like: the way our visual senses respond to distant objects makes the stars appear to be at much the same distance from us. Many cultures, especially in the Middle and Far East, thought of the heavens as a slowly spinning bowl.
2The Great Comet of 1577 is not Halley’s comet, but another of historical importance, now called C/1577 V1. It was visible to the naked eye in 1577 AD. Brahe observed the comet and deduced that comets were located outside the Earth’s atmosphere. The comet is currently about 24 billion kilometres from the Sun.
3The figure was not known until 1798, when Henry Cavendish obtained a reasonably accurate value in a laboratory experiment. It is about 6.67 × 10−11 newton metre squared per kilogram squared.
4June Barrow-Green. Poincaré and the Three Body Problem, American Mathematical Society, Providence 1997.
1In 1535 the mathematicians Antonio Fior and Niccolò Fontana (nicknamed Tartaglia, ‘the stammerer’) engaged in a public contest. They set each other cubic equations to solve, and Tartaglia beat Fior comprehensively. At that time, cubic equations were classified into three distinct types, because negative numbers were not recognised. Fior knew how to solve just one type; initially Tartaglia knew how to solve one different type, but shortly before the contest he figured out how to solve all the other types. He then set Fior only the types that he knew Fior could not solve. Cardano, working on his algebra text, heard about the contest, and realised that Fior and Tartaglia knew how to solve cubics. This discovery would greatly enhance the book, so he asked Tartaglia to reveal his methods.
Eventually Tartaglia divulged the secret, later stating that Cardano had promised never to make it public. But the method appeared in the Ars Magna, so Tartaglia accused Cardano of plagiarism. However, Cardano had an excuse, and he also had a good reason to find a way round his promise. His student Lodovico Ferrari had found how to solve quartic equations, an equally novel and dramatic discovery, and Cardano wanted that in his book, too. However, Ferrari’s method required the solution of an associated cubic equation, so Cardano could not publish Ferrari’s work without also publishing Tartaglia’s.
Then he learned that Fior was a student of Scipio del Ferro, who was rumoured to have solved all three types of cubic, passing just one type on to Fior. Del Ferro’s unpublished papers were in the possession of Annibale del Nave. So Cardano and Ferrari went to Bologna in 1543 to consult del Nave, and in the papers they found solutions to all three types of cubic. So Cardano could honestly say that he was publishing del Ferro’s method, not Tartaglia’s. Tartaglia still felt cheated, and published a long, bitter diatribe against Cardano. Ferrari challenged him to a public debate and won hands down. Tartaglia never really recovered his reputation after that.
1Summarised in Chapter 12of: Ian Stewart. Mathematics of Life, Profile, London 2011.
1Yes, I know this is the plural of ‘die’, but nowadays everyone uses it for the singular as well, and I’ve given up fighting this tendency. It could be worse: someone just sent me an e-mail carefully using ‘dice’ for the singular and ‘die’ for the plural.
2There are many fallacies in Pascal’s argument. The main one is that it would apply to any hypothetical supernatural being.
3The theorem states that under certain (fairly common) conditions, the sum of a large number of random variables will have an approximately normal distribution. More precisely, if (x1, . . ., xn) is a sequence of independent identically distributed random variables, each having mean μ and variance σ2, then the central limit theorem states that
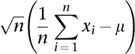
converges to a normal distribution with mean 0 and standard deviation σ as n becomes arbitrarily large.
1Look at three consecutive masses, numbered n − 1, n, n + 1. Suppose that at time t they are displaced distances un−1(t), un(t), and un+1 (t), from their initial positions on the horizontal axis. By Newton’s second law the acceleration of each mass is proportional to the forces that act on it. Make the simplifying assumption that each mass moves through a very small distance in the vertical direction only. To a very good approximation, the force that mass n 1 exerts on mass n is then proportional to the difference un−1(t) − un(t), and similarly the force that mass n + 1 exerts on mass n is proportional to the difference un+1(t)−un(t). Adding these together, the total force exerted on mass n is proportional to un−1(t) − 2un(t) + un+1(t). This is the difference between un−1(t) − un(t) − un+1(t), and each of these expressions is also the difference between the positions of consecutive masses. So the force exerted on mass n is a difference between differences.
Now suppose the masses are very close together. In calculus, a difference – divided by a suitable small constant – is an approximation to a derivative. A difference between differences is an approximation to a derivative of a derivative, that is, a second derivative. In the limit of infinitely many point masses, infinitesimally close together, the force exerted at a given point of the spring is therefore proportional to ∂2u/∂x2, where x is the space coordinate measured along the length of the string. By Newton’s second law this is proportional to the acceleration at right angles to that line, which is the second time derivative ∂2u/∂t2. Writing the constant of proportionality as c2 we get
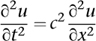
where u(x, t) is the vertical position of location x on the string at time t.
2For an animation see http://en.wikipedia.org/wiki/Wave_equation
3In symbols, the solutions are precisely the expressions
u(x, t) = f(x − ct) + g(x + ct)
for any functions f and g.
4Animations of the first few normal modes of a circular drum can be found at http://en.wikipedia.org/wiki/Vibrations_of_a_circular_drum
Circular and rectangular drum animations are at
http://www.mobiusilearn.com/viewcasestudies.aspx?id=2432
1Suppose that u(x, t) = e−n2αt sin nx. Then
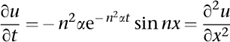
Therefore u(x, t) satisfies the heat equation.
2This is JFIF encoding, used for the web. EXIF coding, for cameras, also includes ‘metadata’ describing the camera settings, such as date, time, and exposure.
1http://www.nasa.gov/topics/earth/features/2010-warmest-year.html
1Donald McDonald. How does a cat fall on its feet?, New Scientist 7 no. 189 (1960) 1647–9. See also http://en.wikipedia.org/wiki/Cat_righting_reflex
2The curl of both sides of the third equation gives
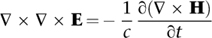
Vector calculus tells us that the left-hand side of this equation simplifies to
∇ × ∇ × E = ∇ (∇ · E) − ∇2E = − ∇2E
where we also use the first equation. Here ∇2 is the Laplace operator. Using the fourth equation, the right-hand side becomes
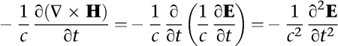
Cancelling out two minus signs and multiplying by c2 yields the wave equation for E:
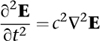
A similar calculation yields the wave equation for H.
1Specifically,
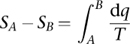
where SA and SB are the entropies in states A and B.
2The second law of thermodynamics is technically an inequality, not an equation. I’ve included the second law in this book because its central position in science demanded its inclusion. It is undeniably a mathematical formula, a loose interpretation of ‘equation’ that is widespread outside the technical scientific literature. The formula alluded to in Note 1 of this chapter, using an integral, is a genuine equation. It defines the change in entropy, but the second law tells us what its most important feature is.
3Brown was anticipated by the Dutch physiologist Jan Ingenhousz, who saw the same phenomenon in coal dust floating on the surface of alcohol, but he didn’t propose any theory to explain what he had seen.
1In the Gran Sasso National Laboratory, in Italy, is a 1300-tonne particle detector called OPERA (oscillation project with emulsion-tracking apparatus). Over two years it tracked 16,000 neutrinos produced at CERN, the European particle physics laboratory in Geneva. Neutrinos are electrically neutral subatomic particles with a very small mass, and they can pass through ordinary matter with ease. The results were baffling: on average the neutrinos completed the 730-kilometre trip 60 nanoseconds (billionths of a second) sooner than they would have done if they had been travelling at the speed of light. The measurements are accurate to within 10 nanoseconds, but there remains the possibility of some systematic error in the way the times are calculated and interpreted, which is highly complex.
The results have been posted online: ‘Measurement of the neutrino velocity with the OPERA detector in the CNGS beam’ by the OPERA Collaboration, http://arxiv.org/abs/1109.4897
This article does not claim to have disproved relativity: it merely presents its observations as something that the team cannot explain with conventional physics. A non-technical report can be found at http://www.nature.com/news/2011/110922/full/news.2011.554.html
A possible source of systematic error, related to differences in the force of gravity at the two laboratories, is proposed at
http://www.nature.com/news/2011/111005/full/news.2011.575.html but the OPERA team disputes this suggestion.
Most physicists think that, despite the great care exercised by the researchers, some systematic error is involved. In particular, previous observations of neutrinos from a supernova seem to conflict with the new ones. The resolution of the controversy will require independent experiments, and these will take several years. Theoretical physicists are already analysing potential explanations ranging from minor, well-known extensions of the standard model of particle physics to exotic new physics in which the universe has more dimensions than the usual four. By the time you read this, the story will already have moved on.
2A thorough explanation is given by Terence Tao on his website: http://terrytao.wordpress.com/2007/12/28/einsteins-derivation-of-emc2/
The derivation of the equation involves five steps:
(a) Describe how space and time coordinates transform when the frame of reference is changed.
(b) Use this description to work out how the frequency of a photon transforms when the frame of reference is changed.
(c) Use Planck’s law to work out how the energy and momentum of a photon transform.
(d) Apply conservation of energy and momentum to work out how the energy and momentum of a moving body transform.
(e) Fix the value of an otherwise arbitrary constant in the calculation by comparing the results with Newtonian physics when the velocity of the body is small.
3Ian Stewart and Jack Cohen. Figments of Reality, Cambridge University Press, Cambridge 1997, page 37.
4http://en.wikipedia.org/wiki/Mass%E2%80%93energy_equivalence
5A few didn’t see it that way. Henry Courten, reanalysing photographs of the 1970 solar eclipse, reported the existence of at least seven very tiny bodies in close orbits round the Sun – perhaps evidence of a thinly populated inner asteroid belt. No conclusive evidence of their existence has been found, and they would have to be less than 60 kilometres across. The objects seen in the photographs may just have been passing small comets or asteroids in eccentric orbits. Whatever they were, they weren’t Vulcan.
6The vacuum energy in a cubic centimetre of free space is estimated to be 10−15 joules. According to quantum electrodynamics it should in theory be 10107 joules – wrong by a factor of 10122.
http://en.wikipedia.org/wiki/Vacuum_energy
7Penrose’s work is reported in: Paul Davies. The Mind of God, Simon & Schuster, New York 1992.
8Joel Smoller and Blake Temple. A one parameter family of expanding wave solutions of the Einstein equations that induces an anomalous acceleration into the standard model of cosmology. http://arxiv.org/abs/0901.1639
9R.S. MacKay and C.P. Rourke. A new paradigm for the universe, preprint, University of Warwick 2011. For more details see the papers listed on http://msp.warwick.ac.uk/~cpr/paradigm/
1The Copenhagen interpretation is usually said to have emerged from discussions between Niels Bohr, Werner Heisenberg, Max Born, and others, in the mid-1920s. It acquired the name because Bohr was Danish, but none of the physicists involved used the term at the time. Don Howard has suggested that the name, and the viewpoint that it encapsulates, first appeared in the 1950s, probably through Heisenberg. See: D. Howard. ‘Who Invented the “Copenhagen Interpretation”? A Study in Mythology’, Philosophy of Science 71 (2004) 669–682.
2Our cat Harlequin can often be observed in a superposition of the states ‘asleep’ and ‘snoring’, but that probably doesn’t count.
3Two science fiction novels about this are Philip K. Dick’s The Man in the High Castle and Norman Spinrad’s The Iron Dream. Thriller writer Len Deighton’s SS-GB is also set in a counterfactual Nazi-ruled England.
1Suppose I roll a dice [see Note 1 of Chapter 7] and assign symbols a, b, c like this:
a The dice rolls 1, 2, or 3
b The dice rolls 4 or 5
c The dice rolls 6
Symbol a occurs with probability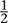 
, symbol b has probability 
, and symbol c has probability 
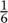. Then my formula, whatever it is, will assign an information content H(, , ).
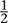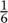However, I could think of this experiment in a different way. First I decide whether the dice rolls something less than or equal to 3, or greater. Call these possibilities q and r, so that
r The dice rolls 4, 5, or 6
Now q has probability 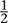and r has probability 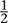. Each conveys information H (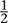,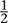). Case q is my original a, and case r is my original b and c. I can split case r into b and c, and their probabilities are 
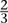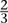and given that r has happened. If we now consider only this case, the information conveyed by whichever of b and c turns up is H(, ). Shannon now insists that the original information should be related to the information in these subcases like this:
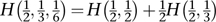
See Figure 61.
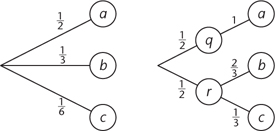
Fig 61 Combining choices in different ways. The information should be the same in either case.
The factor 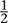in front of the final H is present because this second choice occurs only half the time, namely when r is chosen in the first stage. There is no such factor in front of the H just after the equals sign, because this refers to a choice that is always made – between q and r.
2See Chapter 2of: C.E. Shannon and W. Weaver. The Mathematical Theory of Communication, University of Illinois Press, Urbana 1964.
1If the population xt is relatively small, so that is close to zero, then 1 −xt is close to 1. The next generation will therefore have a size close to kxt, which is k times as large as the current one. As the size of the population increases, the extra factor 1 − xt makes the actual growth rate smaller, and it drops to zero as the population approaches its theoretical maximum.
2R.F. Costantino, R.A. Desharnais, J.M. Cushing, and B. Dennis. Chaotic dynamics in an insect population, Science 275 (1997) 389–391.
3J. Huisman and F.J. Weissing. Biodiversity of plankton by species oscillations and chaos, Nature 402 (1999) 407–410.
4E. Benincà, J. Huisman, R. Heerkloss, K.D. Jöhnk, P. Branco, E.H. Van Nes, M. Scheffer, and S.P. Ellner. Chaos in a long-term experiment with a plankton community, Nature 451 (2008) 822–825.
1The value of a call option is
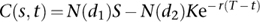
where
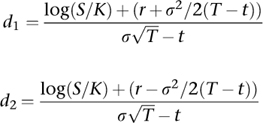
The price of a corresponding put option is
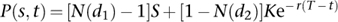
Here N(dj) is the cumulative distribution function of the standard normal distribution for j = 1, 2, and T – t is the time to maturity.
2Strictly, a Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel.
3M. Poovey. Can numbers ensure honesty? Unrealistic expectations and the U.S. accounting scandal, Notices of the American Mathematical Society 50 (2003) 27–35.
4A.G. Haldane and R.M. May. Systemic risk in banking ecosystems, Nature 469 (2011) 351–355.