Just as Albert Einstein, with his startled mop hairdo, is the archetypal scientist in popular culture, so his equation E=mc2 is the archetypal equation. It is widely believed that the equation led to the invention of nuclear weapons, that it comes from Einstein’s theory of relativity, and that this theory (obviously) has something to do with various things being relative. In fact, many social relativists happily chant ‘everything is relative’, and think it has something to do with Einstein.
It doesn’t. Einstein named his theory ‘relativity’ because it was a modification of the rules for relative motion that had traditionally been used in Newtonian mechanics, where motion is relative, depending in a very simple and intuitive way on the frame of reference in which it is observed. Einstein had to tweak Newtonian relativity to make sense of a baffling experimental discovery: that one particular physical phenomenon is not relative at all, but absolute. From this he derived a new kind of physics in which objects shrink when they move very fast, time slows to a crawl, and mass increases without limit. An extension incorporating gravity has given us the best understanding we yet have of the origins of the universe and the structure of the cosmos. It is based on the idea that space and time can be curved.
Relativity is real. The Global Positioning System (GPS, used among other things for car satnav) works only when corrections are made for relativistic effects. The same goes for particle accelerators such as the Large Hadron Collider, currently searching for the Higgs boson, thought to be the origin of mass. Modern communications have become so fast that market traders are beginning to run up against a relativistic limitation: the speed of light. This is the fastest that any message, such as an Internet instruction to buy or sell stock, can travel. Some see this as an opportunity to cut a deal nanoseconds earlier than the competition, but so far, relativistic effects haven’t had a serious effect on international finance. However, people have already worked out the best locations for new stock markets or dealerships. It’s only a matter of time.
At any rate, not only is relativity not relative: even the iconic equation is not what it seems. When Einstein first derived the physical idea that it represents, he didn’t write it in the familiar way. It is not a mathematical consequence of relativity, though it becomes one if various physical assumptions and definitions are accepted. It is perhaps typical of human culture that our most iconic equation is not, and was not, what it seems to be, and neither is the theory that gave birth to it. Even the connection with nuclear weapons is not clear-cut, and its historical influence on the first atomic bomb was small compared with Einstein’s political clout as the iconic scientist.
‘Relativity’ covers two distinct but related theories: special relativity and general relativity. I’ll use Einstein’s celebrated equation as an excuse to talk about both. Special relativity is about space, time, and matter in the absence of gravity; general relativity takes gravity into account as well. The two theories are part of one big picture, but it took Einstein ten years of intensive effort to discover how to modify special relativity to incorporate gravity. Both theories were inspired by difficulties in reconciling Newtonian physics with observations, but the iconic formula arose in special relativity.
Physics seemed fairly straightforward and intuitive in Newton’s day. Space was space, time was time, and never the twain should meet. The geometry of space was that of Euclid. Time was independent of space, the same for all observers – provided they had synchronised their clocks. The mass and size of a body did not change when it moved, and time always passed at the same rate everywhere. But when Einstein had finished reformulating physics, all of these statements – so intuitive that it is very difficult to imagine how any of them could fail to represent reality – turned out to be wrong.
They were not totally wrong, of course. If they had been nonsense, then Newton’s work would never have got off the ground. The Newtonian picture of the physical universe is an approximation, not an exact description. The approximation is extremely accurate provided everything involved is moving slowly enough, and in most everyday circumstances that is the case. Even a jet fighter, travelling at twice the speed of sound, is moving slowly for this purpose. But one thing that does play a role in everyday life moves very fast indeed, and sets the yardstick for all other speeds: light. Newton and his successors had demonstrated that light was a wave, and Maxwell’s equations confirmed this. But the wave nature of light raised a new issue. Ocean waves are waves in water, sound waves are waves in air, earthquakes are waves in the Earth. So light waves are waves in. . . what?
Mathematically they are waves in the electromagnetic field, which is assumed to pervade the whole of space. When the electromagnetic field is excited – persuaded to support electricity and magnetism – we observe a wave. But what happens when it’s not excited? Without waves, an ocean would still be an ocean, air would still be air, and the Earth would still be the Earth. Analogously, the electromagnetic field would still be. . . the electromagnetic field. But you can’t observe the electromagnetic field if there’s no electricity or magnetism going on. If you can’t observe it, what is it? Does it exist at all?
All waves known to physics, except the electromagnetic field, are waves in something tangible. All three types of wave – water, air, earthquake – are waves of movement. The medium moves up and down or from side to side, but usually it doesn’t travel with the wave. (Tie a long rope to a wall and shake one end: a wave travels along the rope. But the rope doesn’t travel along the rope.) There are exceptions: when air travels along with the wave we call it ‘wind’, and ocean waves move water up a beach when they hit one. But even though we describe a tsunami as a moving wall of water, it doesn’t roll across the top of the ocean like a football rolling along the pitch. Mostly, the water in any given location goes up and down. It is the location of the ‘up’ that moves. Until the water gets close to shore; then you get something much more like a moving wall.
Light, and electromagnetic waves in general, didn’t seem to be waves in anything tangible. In Maxwell’s day, and for fifty years or more afterwards, that was disturbing. Newton’s law of gravity had long been criticised because it implies that gravity somehow ‘acts at a distance’, as miraculous in philosophical principle as kicking a ball into the goal when you’re sitting in the stands. Saying that it is transmitted by ‘the gravitational field’ doesn’t really explain what’s happening. The same goes for electromagnetism. So physicists came round to the idea that there was some medium – no one knew what, they called it the ‘luminiferous aether’ or just plain ‘ether’ – that supported electromagnetic waves. Vibrations travel faster the more rigid the medium, and light was very fast indeed, so the ether had to be extremely rigid. Yet planets could move through it without resistance. To have avoided easy detection, the ether must have no mass, no viscosity, be incompressible, and be totally transparent to all forms of radiation.
It was a daunting combination of attributes, but almost all physicists assumed the ether existed, because light clearly did what light did. Something had to carry the wave. Moreover, the ether’s existence could in principle be detected, because another feature of light suggested a way to observe it. In a vacuum, light moves with a fixed speed c. Newtonian mechanics had taught every physicist to ask: speed relative to what? If you measure a velocity in two different frames of reference, one moving with respect to the other, you get different answers. The constancy of the speed of light suggested an obvious reply: relative to the ether. But this was a little facile, because two frames of reference that are moving with respect to each other can’t both be at rest relative to the ether.
As the Earth ploughs its way through the ether, miraculously unresisted, it goes round and round the Sun. At opposite points on its orbit it is moving in opposite directions. So by Newtonian mechanics, the speed of light should vary between two extremes: c plus a contribution from the Earth’s motion relative to the ether, and c minus the same contribution. Measure the speed, measure it six months later, find the difference: if there is one, you have proof that the ether exists. In the late 1800s many experiments along these lines were carried out, but the results were inconclusive. Either there was no difference, or there was one but the experimental method wasn’t accurate enough. Worse, the Earth might be dragging the ether along with it. This would simultaneously explain why the Earth can move through such a rigid medium without resistance, and imply that you ought not to see any difference in the speed of light anyway. The Earth’s motion relative to the ether would always be zero.
In 1887 Albert Michelson and Edward Morley carried out one of the most famous physics experiments of all time. Their apparatus was designed to detect extremely small variations in the speed of light in two directions, at right angles to each other. However the Earth was moving relative to the ether, it couldn’t be moving with the same relative speed in two different directions. . . unless it happened by coincidence to be moving along the line bisecting those directions, in which case you just rotated the apparatus a little and tried again.
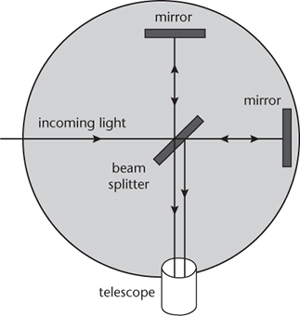
The apparatus, Figure 48, was small enough to fit on a laboratory desk. It used a half-silvered mirror to split a beam of light into two parts, one passing through the mirror and the other being reflected at right angles. Each separate beam was reflected back along its path, and the two beams combined again, to hit a detector. The apparatus was adjusted to make the paths the same length. The original beam was set up to be coherent, meaning that its waves were in synchrony with each other – all having the same phase, peaks coinciding with peaks. Any difference between the speed of light in the directions followed by the two beams would cause their phases to shift relative to each other, so their peaks would be in different places. This would cause interference between the two waves, resulting in a striped pattern of ‘diffraction fringes’. Motion of the Earth relative to the ether would cause the fringes to move. The effect would be tiny: given what was known about the Earth’s motion relative to the Sun, the diffraction fringes would shift by about 4% of the width of one fringe. By using multiple reflections, this could be increased to 40%, big enough to be detected. To avoid the possible coincidence of the Earth moving exactly along the bisector of the two beams, Michelson and Morley floated the apparatus on a bath of mercury, so that it could be spun round easily and rapidly. It should then be possible to watch the fringes shifting with equal rapidity.
Fig 48 The Michelson-Morley experiment.
It was a careful, accurate experiment. Its result was entirely negative. The fringes did not move by 40% of their width. As far as anyone could tell with certainty, they didn’t move at all. Later experiments, capable of detecting a shift 0.07% as wide as a fringe, also gave a negative result. The ether did not exist.
This result didn’t just dispose of the ether: it threatened to dispose of Maxwell’s theory of electromagnetism, too. It implied that light does not behave in a Newtonian manner, relative to moving frames of reference. This problem can be traced right back to the mathematical properties of Maxwell’s equations and how they transform relative to a moving frame. The Irish physicist and chemist George FitzGerald and the Dutch physicist Hendrik Lorenz independently suggested (in 1892 and 1895 respectively) an audacious way to get round the problem. If a moving body contracts slightly in its direction of motion, by just the right amount, then the change in phase that the Michelson–Morley experiment was hoping to detect would be exactly cancelled out by the change in the length of the path that the light was following. Lorenz showed that this ‘Lorenz–FitzGerald contraction’ sorted out the mathematical difficulties with the Maxwell equations as well. The joint discovery showed that the results of experiments on electromagnetism, including light, do not depend on the relative motion of the reference frame. Poincaré, who had also been working along similar lines, added his persuasive intellectual weight to the idea.
The stage was now set for Einstein. In 1905 he developed and extended previous speculations about a new theory of relative motion in a paper ‘On the electrodynamics of moving bodies’. His work went beyond that of his predecessors in two ways. He showed that the necessary change to the mathematical formulation of relative motion was more than just a trick to sort out electromagnetism. It was required for all physical laws. It followed that the new mathematics must be a genuine description of reality, with the same philosophical status that had been accorded to the prevailing Newtonian description, but providing a better agreement with experiments. It was real physics.
The view of relative motion employed by Newton went back even further, to Galileo. In his 1632 Dialogo sopra i due massimi sistemi del mondo (‘Dialogue Concerning the Two Chief World Systems’) Galileo discussed a ship travelling at constant velocity on a perfectly smooth sea, arguing that no experiment in mechanics carried out below decks could reveal that the ship was moving. This is Galileo’s principle of relativity: in mechanics, there is no difference between observations made in two frames that are moving with uniform velocity relative to each other. In particular, there is no special frame of reference that is ‘at rest’. Einstein’s starting-point was the same principle, but with an extra twist: it must apply not just to mechanics, but to all physical laws. Among them, of course, being Maxwell’s equations and the constancy of the speed of light.
To Einstein, the Michelson–Morley experiment was a small piece of extra evidence, but it wasn’t proof of the pudding. The proof that his new theory was correct lay in his extended principle of relativity, and what it implied for the mathematical structure of the laws of physics. If you accepted the principle, all else followed. This is why the theory became known as ‘relativity’. Not because ‘everything is relative’, but because you have to take into account the manner in which everything is relative. And it’s not what you expect.
This version of Einstein’s theory is known as special relativity because it applies only to frames of reference that are moving uniformly with respect to each other. Among its consequences are the Lorenz–FitzGerald contraction, now interpreted as a necessary feature of space-time. In fact, there were three related effects. If one frame of reference is moving uniformly relative to another one, then lengths measured in that frame contract along the direction of motion, masses increase, and time runs more slowly. These three effects are tied together by the basic conservation laws of energy and momentum; once you accept one of them, the others are logical consequences.
The technical formulation of these effects is a formula that describes how measurements in one frame relate to those in the other. The executive summary is: if a body could move close to the speed of light, then its length would become very small, time would slow to a crawl, and its mass would become very large. I’ll just give a flavour of the mathematics: the physical description should not be taken too literally and it would take too long to set it up in the correct language. It all comes from. . . Pythagoras’s theorem. One of the oldest equations in science leads to one of the newest.
Suppose that a spaceship is passing overhead with velocity v, and the crew performs an experiment. They send a pulse of light from the floor of the cabin to the roof, and measure the time taken to be T. Meanwhile an observer on the ground watches the experiment through a telescope (assume the spaceship is transparent), measuring the time to be t.
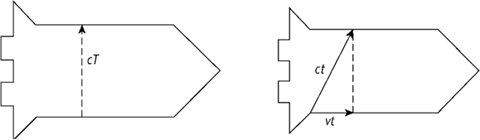
Fig 49 Left: The experiment in the crew’s frame of reference. right: The same experiment in the ground observer’s frame of reference. Grey shows the ship’s position as seen from the ground when the light beam starts its journey; black shows the ship’s position when the light completes its journey.
Figure 49 (left) shows the geometry of the experiment from the crew’s point of view. To them, the light has gone straight up. Since light travels at speed c, the distance travelled is cT, shown by the dotted arrow. Figure 49 (right) shows the geometry of the experiment from the ground observer’s point of view. The spaceship has moved a distance vt, so the light has travelled diagonally. Since light also travels at speed c for the ground observer, the diagonal has length ct. But the dotted line has the same length as the dotted arrow in the first picture, namely cT. By Pythagoras’s theorem,
(ct)2 = (CT)2 + (vt)2
We solve for T, getting
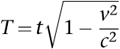
which is smaller than t.
To derive the Lorenz-FitzGerald contraction, we now imagine that the spaceship travels to a planet distance x from Earth at speed v. Then the elapsed time is t=x/v. But the previous formula shows that to the crew, the time taken is T, not t. For them, the distance X must satisfy T=X/v. Therefore
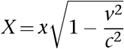
which is smaller than x.
The derivation of the mass change is slightly more involved, and it depends on a particular interpretation of mass, ‘rest mass’, so I won’t give details. The formula is
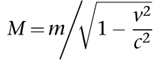
which is larger than m.
These equations tell us that there is something very special about the speed of light (and indeed about light). An important consequence of this formalism is that the speed of light is an impenetrable barrier. If a body starts out slower than light, it cannot be accelerated to a speed greater than that of light. In September 2011 physicists working in Italy announced that subatomic particles called neutrinos appeared to be travelling faster than light.1 Their observation is controversial, but if it is confirmed, it will lead to important new physics.
Pythagoras turns up in relativity in other ways. One is the formulation of special relativity in terms of the geometry of space-time, originally introduced by Hermann Minkowski. Ordinary Newtonian space can be captured mathematically by making its points correspond to three coordinates (x, y, z), and defining the distance d between such a point and another one (X, Y, Z) using Pythagoras’s theorem:
d2 = (x–X)2 + (y –Y)2 + (z–Z)2
Now take the square root to get d. Minkowski space-time is similar, but now there are four coordinates (x, y, z, t), three of space plus one of time, and a point is called an event – a location in space, observed at a specified time. The distance formula is very similar:
d2 = (x–X)2 + (y–Y)2 +(z–Z)2–c2(t–T)2
The factor c2 is just a consequence of the units used to measure time, but the minus sign in front of it is crucial. The ‘distance’ d is called the interval, and the square root is real only when the right-hand side of the equation is positive. That boils down to the spatial distance between the two events being larger than the temporal difference (in correct units: light-years and years, for instance). That in turn means that in principle a body could travel from the first point in space at the first time, and arrive at the second point in space at the second time, without going faster than light.
In other words, the interval is real if and only if it is physically possible, in principle, to travel between the two events. The interval is zero if and only if light could travel between them. This physically accessible region is called the light cone of an event, and it comes in two pieces: the past and the future. Figure 50 shows the geometry when space is reduced to one dimension.
I’ve now shown you three relativistic equations, and sketched how they arose, but none of them is Einstein’s iconic equation. However, we’re now ready to understand how he derived it, once we appreciate one more innovation of early twentieth-century physics. As we’ve seen, physicists had previously performed experiments to demonstrate conclusively that light is a wave, and Maxwell had shown that it is a wave of electromagnetism. However, by 1905 it was becoming clear that despite the weight of evidence for the wave nature of light, there are circumstances in which it behaves like a particle. In that year Einstein used this idea to explain some features of the photoelectric effect, in which light that hits a suitable metal generates electricity. He argued that the experiments made sense only if light comes in discrete packages: in effect, particles. They are now called photons.
Fig 50 Minkowski space-time, with space shown as one-dimensional.
This puzzling discovery was one of the key steps towards quantum mechanics, and I’ll say more about it in Chapter 14. Curiously, this quintessentially quantum-mechanical idea was vital to Einstein’s formulation of relativity. To derive his equation relating mass to energy, Einstein thought about what happens to a body that emits a pair of photons. To simplify the calculations he restricted attention to one dimension of space, so that the body moved along a straight line. This simplification does not affect the answer. The basic idea is to consider the system in two different frames of reference.2 One moves with the body, so that the body appears to be stationary within that frame. The other frame moves with a small, nonzero velocity relative to the body. Let me call these the stationary and moving frames. They are like the spaceship (in its own frame of reference it is stationary) and my ground observer (to whom it appears to be moving).
Einstein assumed that the two photons are equally energetic, but emitted in opposite directions. Their velocities are equal and opposite, so the velocity of the body (in either frame) does not change when the photons are emitted. Then he calculated the energy of the system before the body emits the pair of photons, and afterwards. By assuming that energy must be conserved, he obtained an expression that relates the change in the body’s energy, caused by emitting the photons, to the change in its (relativistic) mass. The upshot was:
(change in energy) = (change in mass) × c2
Making the reasonable assumption that a body of zero mass has zero energy, it then followed that
energy = mass × c2
This, of course, is the famous formula, in which E symbolises energy and m mass.
As well as doing the calculations, Einstein had to interpret their meaning. In particular, he argued that in a frame for which the body is at rest, the energy given by the formula should be considered to be its ‘internal’ energy, which it possesses because it is made from subatomic particles, each of which has its own energy. In a moving frame, there is also a contribution from kinetic energy. There are other mathematical subtleties too, such as the use of a small velocity and approximations to the exact formulas.
Einstein is often credited, if that’s the word, with the realisation that an atomic bomb would release stupendous quantities of energy. Certainly Time magazine gave that impression in July 1946 when it put his face on the cover with an atomic mushroom cloud in the background bearing his iconic equation. The connection between the equation and a huge explosion seems clear: the equation tells us that the energy inherent in any object is its mass multiplied by the square of the speed of light. Since the speed of light is huge, its square is even bigger, which equates to a lot of energy in a small amount of matter. The energy in one gram of matter turns out to be 90 terajoules, equivalent to about one day’s output of electricity from a nuclear power station.
However, it didn’t happen like that. The energy released in an atomic bomb is only a tiny fraction of the relativistic rest mass, and physicists were already aware, on experimental grounds, that certain nuclear reactions could release a lot of energy. The main technical problem was to hold a lump of suitable radioactive material together long enough to get a chain reaction, in which the decay of one radioactive atom causes it to emit radiation that triggers the same effect in other atoms, growing exponentially. Nevertheless, Einstein’s equation quickly became established in the public mind as the progenitor of the atomic bomb. The Smyth report, an American government document released to the public to explain the atomic bomb, placed the equation on its second page. I suspect that what happened is what Jack Cohen and I have called ‘lies to children’ – simplified stories told for legitimate purposes, which pave the way to more accurate enlightenment.3 This is how education works: the full story is always too complicated for anyone except the experts, and they know so much that they don’t believe most of it.
However, Einstein’s equation can’t just be dismissed out of hand. It did play a role in the development of nuclear weapons. The notion of nuclear fission, which powers the atom bomb, arose from discussions between the physicists Lise Meitner and Otto Frisch in Nazi Germany in 1938. They were trying to understand the forces that held the atom together, which were a bit like the surface tension of a drop of liquid. They were out walking, discussing physics, and they applied Einstein’s equation to work out whether fission was possible on energy grounds. Frisch later wrote:4
We both sat down on a tree trunk and started to calculate on scraps of paper. . . When the two drops separated they would be driven apart by electrical repulsion, about 200 MeV in all. Fortunately Lise Meitner remembered how to compute the masses of nuclei. . . and worked out that the two nuclei formed. . . would be lighter by about one-fifth the mass of a proton. . . according to Einstein’s formula E = mc2. . . the mass was just equivalent to 200 MeV. It all fitted!
Although E = mc2 was not directly responsible for the atom bomb, it was one of the big discoveries in physics that led to an effective theoretical understanding of nuclear reactions. Einstein’s most important role regarding the atomic bomb was political. Urged by Leo Szilard, Einstein wrote to President Roosevelt, warning that the Nazis might be developing atomic weapons and explaining their awesome power. His reputation and influence were enormous, and the president heeded the warning. The Manhattan Project, Hiroshima and Nagasaki, and the ensuing Cold War were just some of the consequences.
Einstein wasn’t satisfied with special relativity. It provided a unified theory of space, time, matter, and electromagnetism, but it missed out one vital ingredient.
Gravity.
Einstein believed that ‘all the laws of physics’ must satisfy his extended version of Galileo’s principle of relativity. The law of gravitation surely ought to be among them. But that wasn’t the case for the current version of relativity. Newton’s inverse square law did not transform correctly between frames of reference. So Einstein decided he had to change Newton’s law. He’d already changed virtually everything else in the Newtonian universe, so why not?
It took him ten years. His starting-point was to work out the implications of the principle of relativity for an observer moving freely under the influence of gravity – in a lift that is dropping freely, for example. Eventually he homed in on a suitable formulation. In this he was aided by a close friend, the mathematician Marcel Grossmann, who pointed him towards a rapidly growing field of mathematics: differential geometry. This had developed from Riemann’s concept of a manifold and his characterisation of curvature, discussed in Chapter 1. There I mentioned that Riemann’s metric can be written as a 3 × 3 matrix, and that technically this is a symmetric tensor. A school of Italian mathematicians, notably Tullio Levi-Civita and Gregorio Ricci-Curbastro, took up Riemann’s ideas and developed them into tensor calculus.
From 1912, Einstein was convinced that the key to a relativistic theory of gravity required him to reformulate his ideas using tensor calculus, but in a 4-dimensional space-time rather than 3-dimensional space. The mathematicians were happily following Riemann and allowing any number of dimensions, so they had already set things up in more than enough generality. To cut a long story short, he eventually derived what we now call the Einstein field equations, which he wrote as:
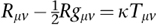
Here R, g, and T are tensors – quantities that define physical properties and transform according to the rules of differential geometry – and κ is a constant. The subscripts μ and v run over the four coordinates of space-time, so each tensor is a 4 × 4 table of 16 numbers. Both are symmetric, meaning that they don’t change when μ and v are swapped, which reduces them to a list of 10 distinct numbers. So really the formula packages together 10 equations, which is why we often refer to them using the plural – compare Maxwell’s equations. R is Riemann’s metric: it defines the shape of space-time. g is the Ricci curvature tensor, which is a modification of Riemann’s notion of curvature. And T is the energy–momentum tensor, which describes how these two fundamental quantities depend on the space-time event concerned. Einstein presented his equations to the Prussian Academy of Science in 1915. He called his new work the general theory of relativity.
We can interpret Einstein’s equations geometrically, and when we do, they provide a new approach to gravity. The basic innovation is that gravity is not represented as a force, but as the curvature of space-time. In the absence of gravity, space-time reduces to Minkowski space. The formula for the interval determines the corresponding curvature tensor. Its interpretation is ‘not curved’, just as Pythagoras’s theorem applies to a flat plane but not to a positively or negatively curved non-Euclidean space. Minkowski space-time is flat. But when gravity occurs, space-time bends.
The usual way to picture this is to forget time, drop the dimensions of space down to two, and get something like Figure 51 (left). The flat plane of Minkowski space(-time) is distorted, shown here by an actual bend, creating a depression. Far from the star, matter or light travels in a straight line (dotted). But the curvature causes the path to bend. In fact, it looks superficially as though some force coming from the star attracts the matter towards it. But there is no force, just warped space-time. However, this image of curvature deforms space along an extra dimension, which is not required mathematically. An alternative image is to draw a grid of geodesics, shortest paths, equally spaced according to the curved metric. They bunch together where the curvature is greater, Figure 51 (right).
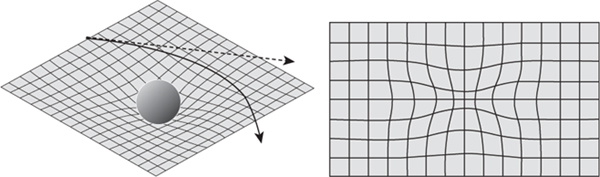
Fig 51 Left: Warped space near a star, and how it bends the paths of passing matter or light. right: alternative image using a grid of geodesics, which bunch together in regions of higher curvature.
If the curvature of space-time is small, that is, if what (in the old picture) we think of as gravitational forces are not too large, then this formulation leads to Newton’s law of gravity. Comparing the two theories, Einstein’s constant κ turns out to be 8πG/c4, where G is Newton’s gravitational constant. This links the new theory to the old one, and proves that in most cases the new one will agree with the old. The interesting new physics occurs when this is no longer true: when gravity is large. When Einstein came up with his theory, any test of relativity had to take place outside the laboratory, on a grand scale. Which meant astronomy.
Einstein therefore went looking for unexplained peculiarities in the motion of the planets, effects that didn’t square with Newton. He found one that might be suitable: an obscure feature of the orbit of Mercury, the planet closest to the Sun, subjected to the greatest gravitational forces – and so, if Einstein was right, inside a region of high curvature.
Like all planets, Mercury follows a path that is very close to an ellipse, so some points in its orbit are closer to the Sun than others. The closest of all is called its perihelion (‘near Sun’ in Greek). The exact location of this perihelion had been observed for many years, and there was something funny about it. The perihelion slowly rotated about the Sun, an effect called precession; in effect, the long axis of the orbital ellipse was slowly changing direction. That was all right; Newton’s laws predicted it, because Mercury is not the only planet in the Solar System and other planets were slowly changing its orbit. The problem was that Newtonian calculations gave the wrong rate of precession. The axis was rotating too quickly.
That had been known since 1840 when François Arago, director of the Paris Observatory, asked Urbain Le Verrier to calculate the orbit of Mercury using Newton’s laws of motion and gravitation. But when the results were tested by observing the exact timing of a transit of Mercury – a passage across the face of the Sun, as viewed from Earth – they were wrong. Le Verrier decided to try again, eliminating potential sources of error, and in 1859 he published his new results. On the Newtonian model, the rate of precession was accurate to about 0.7%. The difference compared with observations was tiny: 38 seconds of arc every century (later revised to 43 arc-seconds). That’s not much, less than one ten thousandth of a degree per year, but it was enough to interest Le Verrier. In 1846 he had made his reputation by analysing irregularities in the orbit of Uranus and predicting the existence, and location, of a then undiscovered planet: Neptune. Now he was hoping to repeat the feat. He interpreted the unexpected perihelion movement as evidence that some unknown world was perturbing Mercury’s orbit. He did the sums and predicted the existence of a small planet with an orbit closer to the Sun than that of Mercury. He even had a name for it: Vulcan, the Roman god of fire.
Observing Vulcan, if it existed, would be difficult. The glare of the Sun was an obstacle, so the best bet was to catch Vulcan in transit, where it would be a tiny dark dot against the bright disc of the Sun. Shortly after Le Verrier’s prediction, an amateur astronomer named Edmond Lescarbault informed the distinguished astronomer that he had seen just that. He had initially assumed that the dot must be a sunspot, but it moved at the wrong speed. In 1860 Le Verrier announced the discovery of Vulcan to the Paris Academy of Science, and the government awarded Lescarbault the prestigious Légion d’Honneur.
Amid the clamour, some astronomers remained unimpressed. One was Emmanuel Liais, who had been studying the Sun with much better equipment than Lescarbault. His reputation was on the line: he had been observing the Sun for the Brazilian government, and it would have been disgraceful to have missed something of such importance. He flatly denied that a transit had taken place. For a time, everything got very confused. Amateurs repeatedly claimed they had seen Vulcan, sometimes years before Le Verrier announced his prediction. In 1878 James Watson, a professional, and Lewis Swift, an amateur, said they had seen a planet like Vulcan during a solar eclipse. Le Verrier had died a year earlier, still convinced he had discovered a new planet near the Sun, but without his enthusiastic new calculations of orbits and predictions of transits – none of which happened – interest in Vulcan quickly died away. Astronomers became skeptical.
In 1915, Einstein administered the coup de grâce. He reanalysed the motion using general relativity, without assuming any new planet, and a simple and transparent calculation led him to a value of 43 seconds of arc for the precession – the exact figure obtained by updating Le Verrier’s original calculations. A modern Newtonian calculation predicts a precession of 5560 arc seconds per century, but observations give 5600. The difference is 40 seconds of arc, so about 3 arc-seconds per century remains unaccounted for. Einstein’s announcement did two things: it was seen as a vindication of relativity, and as far as most astronomers were concerned, it relegated Vulcan to the scrapheap.5
Another famous astronomical verification of general relativity is Einstein’s prediction that the Sun bends light. Newtonian gravitation also predicts this, but general relativity predicts an amount of bending that is twice as large. The total solar eclipse of 1919 provided an opportunity to distinguish the two, and Sir Arthur Eddington mounted an expedition, eventually announcing that Einstein prevailed. This was accepted with enthusiasm at the time, but later it became clear that the data were poor, and the result was questioned. Further independent observations from 1922 seemed to agree with the relativistic prediction, as did a later reanalysis of Eddington’s data. By the 1960s it became possible to make the observations for radio-frequency radiation, and only then was it certain that the data did indeed show a deviation twice that predicted by Newton and equal to that predicted by Einstein.
The most dramatic predictions from general relativity arise on a much grander scale: black holes, which are born when a massive star collapses under its own gravitation, and the expanding universe, currently explained by the Big Bang.
Solutions to Einstein’s equations are space-time geometries. These might represent the universe as a whole, or some part of it, assumed to be gravitationally isolated so that the rest of the universe has no important effect. This is analogous to early Newtonian assumptions that only two bodies are interacting, for example. Since Einstein’s field equations involve ten variables, explicit solutions in terms of mathematical formulas are rare. Today we can solve the equations numerically, but that was a pipedream before the 1960s because computers either didn’t exist or were too limited to be useful. The standard way to simplify equations is to invoke symmetry. Suppose that the initial conditions for a space-time are spherically symmetric, that is, all physical quantities depend only on the distance from the centre. Then the number of variables in any model is greatly reduced. In 1916 the German astrophysicist Karl Schwarzschild made this assumption for Einstein’s equations, and managed to solve the resulting equations with an exact formula, known as the Schwarzschild metric. His formula had a curious feature: a singularity. The solution became infinite at a particular distance from the centre, called the Schwarzschild radius. At first it was assumed that this singularity was some kind of mathematical artefact, and its physical meaning was the subject of considerable dispute. We now interpret it as the event horizon of a black hole.
Imagine a star so massive that its radiation cannot counter its gravitational field. The star will begin to contract, sucked together by its own mass. The denser it gets, the stronger this effect becomes, so the contraction happens ever faster. The star’s escape velocity, the speed with which an object must move to escape the gravitational field, also increases. The Schwarzschild metric tells us that at some stage, the escape velocity becomes equal to that of light. Now nothing can escape, because nothing can travel faster than light. The star has become a black hole, and the Schwarzschild radius tells us the region from which nothing can escape, bounded by the black hole’s event horizon.
Black hole physics is complex, and there isn’t space to do it justice here. Suffice it to say that most cosmologists are now satisfied that the prediction is valid, that the universe contains innumerable black holes, and indeed that at least one lurks at the heart of our Galaxy. Indeed, of most galaxies. In 1917 Einstein applied his equations to the entire universe, assuming another kind of symmetry: homogeneity. The universe should look the same (on large enough scale) at all points in space and time. By then he had modified the equations to include a ‘cosmological constant’ Λ, and sorted out the meaning of the constant κ. The equations were now written like this:
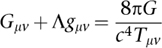
The solutions had a surprising implication: the universe should shrink as time passes. This forced Einstein to add the term involving the cosmological constant: he was seeking an unchanging, stable universe, and by adjusting the constant to the right value he could stop his model universe contracting to a point. In 1922 Alexander Friedmann found another equation, which predicted the universe should expand and did not require the cosmological constant. It also predicted the rate of expansion. Einstein still wasn’t happy: he wanted the universe to be stable and unchanging.
For once Einstein’s imagination failed him. In 1929 American astronomers Edwin Hubble and Milton Humason found evidence that the universe is expanding. Distant galaxies are moving away from us, as shown by shifts in the frequency of the light they emit – the famous Doppler effect, in which the sound of a speeding ambulance drops as it passes by, because the sound waves are affected by the relative speed of emitter and receiver. Now the waves are electromagnetic and the physics is relativistic, but there is still a Doppler effect. Not only do distant galaxies move away from us: the more distant they are, the faster they recede.
Running the expansion backwards in time, it turns out that at some point in the past, the entire universe was essentially just a point. Before that, it didn’t exist at all. At that primeval point, space and time both came into existence in the famous Big Bang, a theory proposed by French mathematician Georges Lemaître in 1927, and almost universally ignored. When radio telescopes observed the cosmological microwave background radiation in 1964, at a temperature that fitted the Big Bang model, cosmologists decided Lemaître had been right after all. Again, the topic deserves a book of is own, and many have been written. Suffice it to say that our current most widely accepted theory of cosmology is an elaboration of the Big Bang scenario.
Scientific knowledge, however, is always provisional. New discoveries can change it. The Big Bang has been the accepted cosmological paradigm for the last 30 years, but it is beginning to show some cracks. Several discoveries either cast serious doubt on the theory, or require new physical particles and forces that have been inferred but not observed. There are three main sources of difficulty. I’ll summarise them first, and then discuss each in more detail. The first is galactic rotation curves, which suggest that most of the matter in the universe is missing. The current proposal is that this is a sign of a new kind of matter, dark matter, which constitutes about 90% of the matter in the universe, and is different from any matter yet observed directly on Earth. The second is an acceleration in the expansion of the universe, which requires a new force, dark energy, of unknown origin but modelled using Einstein’s cosmological constant. The third is a collection of theoretical issues related to the popular theory of inflation, which explains why the observable universe is so uniform. The theory fits observations, but its internal logic is looking shaky.
Dark matter first. In 1938 the Doppler effect was used to measure the speeds of galaxies in clusters, and the results were inconsistent with Newtonian gravitation. Because galaxies are separated by large distances, space-time is almost flat and Newtonian gravity is a good model. Fritz Zwicky suggested that there must be some unobserved matter to account for the discrepancy, and it was named dark matter because it could not be seen in photographs. In 1959, using the Doppler effect to measure the speed of rotation of stars in the galaxy M33, Louise Volders discovered that the observed rotation curve – a plot of speed against distance from the centre – was also inconsistent with Newtonian gravitation, which again is a good model. Instead of the speed falling off at greater distances, it remained almost constant, Figure 52. The same problem arises for many other galaxies.
If it exists, dark matter must be different from ordinary ‘baryonic’ matter, the particles observed in experiments on Earth. Its existence is accepted by most cosmologists, who argue that dark matter explains several different anomalies in observations, not just rotation curves. Candidate particles have been suggested, such as WIMPs (weakly interacting massive particles), but so far these particles have not been detected in experiments. The distribution of dark matter around galaxies has been plotted by assuming dark matter exists and working out where it has to be to make the rotation curves flat. It generally seems to form two globes of galactic proportions, one above the plane of the galaxy and the other below it, like a giant dumb-bell. This is a bit like predicting the existence of Neptune from discrepancies in the orbit of Uranus, but such predictions require confirmation: Neptune had to be found.
Fig 52 Galactic rotation curves for M33: theory and observations.
Dark energy is similarly proposed to explain the results of the 1998 High-z Supernova Search Team, which expected to find evidence that the expansion of the universe is slowing down as the initial impulse from the Big Bang dies away. Instead, the observations indicated that the expansion of the universe is speeding up, a finding confirmed by the Supernova Cosmology Project in 1999. It is as though some antigravity force pervades space, pushing galaxies apart at an ever-increasing rate. This force is not any of the four basic forces of physics: gravity, electromagnetism, strong nuclear force, weak nuclear force. It was named dark energy. Again, its existence seemed to solve some other cosmological problems.
Inflation was proposed by the American physicist Alan Guth in 1980 to explain why the universe is extremely uniform in its physical properties on very large scales. Theory showed that the Big Bang ought to have produced a universe that was far more curved. Guth suggested that an ‘inflaton field’ (that’s right, no second i: it’s thought to be a scalar quantum field corresponding to a hypothetical particle, the inflaton) caused the early universe to expand with extreme rapidity. Between 10−36 and 10−32 seconds after the Big Bang, the volume of the universe grew by a mindboggling factor of 1078. The inflaton field has not been observed (this would require unfeasibly high energies) but inflation explains so many features of the universe, and fits observations so closely, that most cosmologists are convinced it happened.
It’s not surprising that dark matter, dark energy, and inflation were popular among cosmologists, because they let them continue to use their favourite physical models, and the results agreed with observations. But things are starting to fall apart.
The distributions of dark matter don’t provide a satisfactory explanation of rotation curves. Enormous amounts of dark matter are needed to keep the rotation curve flat out to the large distances observed. The dark matter has to have unrealistically large angular momentum, which is inconsistent with the usual theories of galaxy formation. The same rather special initial distribution of dark matter is required in every galaxy, which seems unlikely. The dumb-bell shape is unstable because it places the additional mass on the outside of the galaxy.
Dark energy fares better, and it is thought to be some kind of quantum-mechanical vacuum energy, arising from fluctuations in the vacuum. However, current calculations of the size of the vacuum energy are too big by a factor of 10122, which is bad news even by the standards of cosmology.6
The main problems affecting inflation are not observations – it fits those amazingly well – but its logical foundations. Most inflationary scenarios would lead to a universe that differs considerably from ours; what counts is the initial conditions at the time of the Big Bang. In order to match observations, inflation requires the early state of the universe to be very special. However, there are also very special initial conditions that produce a universe just like ours without invoking inflation. Although both sets of conditions are extremely rare, calculations performed by Roger Penrose7 show that the initial conditions that do not require inflation outnumber those that produce inflation by a factor of one googolplex – ten to the power ten to the power 100. So explaining the current state of the universe without inflation would be much more convincing than explaining it with inflation.
Penrose’s calculation relies on thermodynamics, which might not be an appropriate model, but an alternative approach, carried out by Gary Gibbons and Neil Turok, leads to the same conclusion. This is to ‘unwind’ the universe back to its initial state. It turns out that almost all of the potential initial states do not involve a period of inflation, and those that do require it are an exceedingly small proportion. But the biggest problem of all is that when inflation is wedded to quantum mechanics, it predicts that quantum fluctuations will occasionally trigger inflation in a small region of an apparently settled universe. Although such fluctuations are rare, inflation is so rapid and so gigantic that the net result is tiny islands of normal space-time surrounded by ever-growing regions of runaway inflation. In those regions, the fundamental constants of physics can be different from their values in our universe. In effect, anything is possible. Can a theory that predicts anything be testable scientifically?
There are alternatives, and it is starting to look as though they need to be taken seriously. Dark matter might not be another Neptune, but another Vulcan – an attempt to explain a gravitational anomaly by invoking new matter, when what really needs changing is the law of gravitation.
The main well-developed proposal is MOND, modified Newtonian dynamics, proposed by Israeli physicist Mordehai Milgrom in 1983. This modifies not the law of gravity, in fact, but Newton’s second law of motion. It assumes that acceleration is not proportional to force when the acceleration is very small. There is a tendency among cosmologists to assume that the only viable alternative theories are dark matter or MOND – so if MOND disagrees with observations, that leaves only dark matter. However, there are many potential ways to modify the law of gravity, and we are unlikely to find the right one straight away. The demise of MOND has been proclaimed several times, but on further investigation no decisive flaw has yet been found. The main problem with MOND, to my mind, is that it puts into its equations what it hopes to get out; it’s like Einstein modifying Newton’s law to change the formula near a large mass. Instead, he found a radically new way to think of gravity, the curvature of space-time.
Even if we retain general relativity and its Newtonian approximation, there may be no need for dark energy. In 2009, using the mathematics of shock waves, American mathematicians Joel Smoller and Blake Temple showed that there are solutions of Einstein’s field equations in which the metric expands at an accelerating rate.8 These solutions show that small changes to the Standard Model could account for the observed acceleration of galaxies without invoking dark energy.
General relativity models of the universe assume that it forms a manifold; that is, on very large scales the structure smoothes out. However, the observed distribution of matter in the universe is clumpy on very big scales, such as the Sloan Great Wall, a filament composed of galaxies 1.37 billion light years long, Figure 53. Cosmologists believe that on even larger scales the smoothness will become apparent – but to date, every time the range of observations has been extended, the clumpiness has persisted.
Fig 53 The clumpiness of the universe.
Robert MacKay and Colin Rourke, two British mathematicians, have argued that a clumpy universe in which there are many local sources of large curvature could explain all of the cosmological puzzles.9 Such a structure is closer to what is observed than some large-scale smoothing, and is consistent with the general principle that the universe ought to be much the same everywhere. In such a universe there need be no Big Bang; in fact, the whole thing could be in a steady state, and be far, far older than the current figure of 13.8 billion years. Individual galaxies would go through a life cycle, surviving relatively unchanged for around 1016 years. They would have a very massive central black hole. Galactic rotation curves would be flat because of inertial drag, a consequence of general relativity in which a rotating massive body drags space-time round with it in its vicinity. The red shift observed in quasars would be caused by a large gravitational field, not by the Doppler effect, and would not be indicative of an expanding universe – this theory has long been advanced by American astronomer Halton Arp, and never satisfactorily disproved. The alternative model even indicates a temperature of 5°K for the cosmological microwave background, the main evidence (aside from red shift interpreted as expansion) for the Big Bang.
MacKay and Rourke say that their proposal ‘overturns virtually every tenet of current cosmology. It does not, however, contradict any observational evidence.’ It may well be wrong, but the fascinating point is that you can retain Einstein’s field equations unchanged, dispense with dark matter, dark energy, and inflation, and still get behaviour reasonably like all of those puzzling observations. So whatever the theory’s fate, it suggests that cosmologists should consider more imaginative mathematical models before resorting to new and otherwise unsupported physics. Dark matter, dark energy, inflation, each requiring radically new physics that no one has observed. . . In science, even one deus ex machina raises eyebrows. Three would be considered intolerable in anything other than cosmology. To be fair, it’s difficult to experiment on the entire universe, so speculatively fitting theories to observations is about all that can be done. But imagine what would happen if a biologist explained life by some unobservable ‘life field’, let alone suggesting that a new kind of ‘vital matter’ and a new kind of ‘vital energy’ were also necessary – while providing no evidence that any of them existed.
Leaving aside the perplexing realm of cosmology, there are now more homely ways to verify relativity, both special and general, on a human scale. Special relativity can be tested in the laboratory, and modern measuring techniques provide exquisite accuracy. Particle accelerators such as the Large Hadron Collider simply would not work unless the designers took special relativity into account, because the particles that whirl round these machines do so at speeds very close indeed to that of light. Most tests of general relativity are still astronomical, ranging from gravitational lensing to pulsar dynamics, and the level of accuracy is high. A recent NASA experiment in low-Earth orbit, using high-precision gyroscopes, confirmed the occurrence of inertial frame-dragging, but failed to reach the intended precision because of unexpected electrostatic effects. By the time the data were corrected for this problem, other experiments had already achieved the same results.
However, one instance of relativistic dynamics, both special and general, is closer to home: car satellite navigation. The satnav systems used by motorists calculate the car’s position using signals from a network of 24 orbiting satellites, the Global Positioning System. GPS is astonishingly accurate, and it works because modern electronics can reliably handle and measure very tiny instants of time. It is based on very precise timing signals, pulses emitted by the satellites and picked up on the ground. Comparing the signals from several satellites triangulates the location of the receiver to within a few metres. This level of accuracy requires knowing the timing to within about 25 nanoseconds (billionths of a second). Newtonian dynamics doesn’t give correct locations, because two effects that are not accounted for in Newton’s equations alter the flow of time: the satellite’s motion and Earth’s gravitational field.
Special relativity deals with the motion, and it predicts that the atomic clocks on the satellites should lose 7 microseconds (millionths of a second) per day compared with clocks on the ground, thanks to relativistic time dilation. General relativity predicts a gain of 45 microseconds per day caused by the Earth’s gravity. The net result is that the clocks on the satellites gain 38 microseconds per day for relativistic reasons. Small as this may seem, its effect on GPS signals is by no means negligible. An error of 38 microseconds is 38,000 nanoseconds, about 1500 times the error that GPS can tolerate. If the software calculated your car’s location using Newtonian dynamics, your satnav would quickly become useless, because the error would grow at a rate of 10 kilometres per day. Ten minutes from now Newtonian GPS would place you on the wrong street; by tomorrow it would place you in the wrong town. Within a week you’d be in the wrong county; within a month, the wrong country. Within a year, you’d be on the wrong planet. If you disbelieve relativity, but use satnav to plan your journeys, you have some explaining to do.