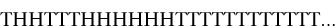
Mathematics is about patterns. The random workings of chance seem to be about as far from patterns as you can get. In fact, one of the current definitions of ‘random’ boils down to ‘lacking any discernible pattern’. Mathematicians had been investigating patterns in geometry, algebra, and analysis for centuries before they realised that even randomness has its own patterns. But the patterns of chance do not conflict with the idea that random events have no pattern, because the regularities of random events are statistical. They are features of a whole series of events, such as the average behaviour over a long run of trials. They tell us nothing about which event occurs at which instant. For example, if you throw a dice1 repeatedly, then about one sixth of the time you will roll 1, and the same holds for 2, 3, 4, 5, and 6 − a clear statistical pattern. But this tells you nothing about which number will turn up on the next throw.
Only in the nineteenth century did mathematicians and scientists realise the importance of statistical patterns in chance events. Even human actions, such as suicide and divorce, are subject to quantitative laws, on average and in the long run. It took time to get used to what seemed at first to contradict free will. But today these statistical regularities form the basis of medical trials, social policy, insurance premiums, risk assessments, and professional sports.
And gambling, which is where it all began.
Appropriately, it was all started by the gambling scholar, Girolamo Cardano. Being something of a wastrel, Cardano brought in much-needed cash by taking wagers on games of chess and games of chance. He applied his powerful intellect to both. Chess does not depend on chance: winning depends on a good memory for standard positions and moves, and an intuitive sense of the overall flow of the game. In a game of chance, however, the player is subject to the whims of Lady Luck. Cardano realised that he could apply his mathematical talents to good effect even in this tempestuous relationship. He could improve his performance at games of chance by having a better grasp of the odds – the likelihood of winning or losing – than his opponents did. He put together a book on the topic, Liber de Ludo Aleae (‘Book on Games of Chance’). It remained unpublished until 1633. Its scholarly content is the first systematic treatment of the mathematics of probability. Its less reputable content is a chapter on how to cheat and get away with it.
One of Cardano’s fundamental principles was that in a fair bet, the stakes should be proportional to the number of ways in which each player can win. For example, suppose the players roll a dice, and the first player wins if he throws a 6, while the second player wins if he throws anything else. The game would be highly unfair if each bet the same amount to play the game, because the first player has only one way to win, whereas the second has five. If the first player bets £1 and the second bets £5, however, the odds become equitable. Cardano was aware that this method of calculating fair odds depends on the various ways of winning being equally likely, but in games of dice, cards, or coin-tossing it was clear how to ensure that this condition applied. Tossing a coin has two outcomes, heads or tails, and these are equally likely if the coin is fair. If the coin tends to throw more heads than tails, it is clearly biased – unfair. Similarly the six outcomes for a fair dice are equally likely, as are the 52 outcomes for a card drawn from a pack.
The logic behind the concept of fairness here is slightly circular, because we infer bias from a failure to match the obvious numerical conditions. But those conditions are supported by more than mere counting. They are based on a feeling of symmetry. If the coin is a flat disc of metal, of uniform density, then the two outcomes are related by a symmetry of the coin (flip it over). For dice, the six outcomes are related by symmetries of the cube. And for cards, the relevant symmetry is that no card differs significantly from any other, except for the value written on its face. The frequencies 1/2, 1/6, and 1/52 for any given outcome rest on these basic symmetries. A biased coin or biased dice can be created by the covert insertion of weights; a biased card can be created using subtle marks on the back, which reveal its value to those in the know.
There are other ways to cheat, involving sleight of hand – say, to swap a biased dice into and out of the game before anyone notices that it always throws a 6. But the safest way to ‘cheat’ – to win by subterfuge – is to be perfectly honest, but to know the odds better than your opponent. In one sense you are taking the moral high ground, but you can improve your chances of finding a suitably naive opponent by rigging not the odds but your opponent’s expectation of the odds. There are many examples where the actual odds in a game of chance are significantly different from what many people would naturally assume.
An example is the game of crown and anchor, widely played by British seamen in the eighteenth century. It uses three dice, each bearing not the numbers 1–6 but six symbols: a crown, an anchor, and the four card suits of diamond, spade, club, and heart. These symbols are also marked on a mat. Players bet by placing money on the mat and throwing the three dice. If any of the symbols that they have bet on shows up, the banker pays them their stake, multiplied by the number of dice showing that symbol. For example, if they bet £1 on the crown, and two crowns turn up, they win £2 in addition to their stake; if three crowns turn up, they win £3 in addition to their stake. It all sounds very reasonable, but probability theory tells us that in the long run a player can expect to lose 8% of his stake.
Probability theory began to take off when it attracted the attention of Blaise Pascal. Pascal was the son of a Rouen tax collector and a child prodigy. In 1646 he was converted to Jansenism, a sect of Roman Catholicism that Pope Innocent X deemed heretical in 1655. The year before, Pascal had experienced what he called his ‘second conversion’, probably triggered by a near-fatal accident when his horses fell off the edge of Neuilly bridge and his carriage nearly did the same. Most of his output from then on was religious philosophy. But just before the accident, he and Fermat were writing to each other about a mathematical problem to do with gambling. The Chevalier de Meré, a French writer who called himself a knight even though he wasn’t, was a friend of Pascal’s, and he asked how the stakes in a series of games of chance should be divided if the contest had to be abandoned part way through. This question was not new: it goes back to the Middle Ages. What was new was its solution. In an exchange of letters, Pascal and Fermat found the correct answer. Along the way they created a new branch of mathematics: probability theory.
A central concept in their solution was what we now call ‘expectation’. In a game of chance, this is a player’s average return in the long run. It would, for example, be 92 pence for crown and anchor with a £1 stake. After his second conversion, Pascal put his gambling past behind him, but he enlisted its aid in a famous philosophical argument, Pascal’s wager.2 Pascal assumed, playing Devil’s advocate, that someone might consider the existence of God to be highly unlikely. In his Pensées (‘Thoughts’) of 1669, Pascal analysed the consequences from the point of view of probabilities:
Let us weigh the gain and the loss in wagering that God is [exists]. Let us estimate these two chances. If you gain, you gain all; if you lose, you lose nothing. Wager, then, without hesitation that He is. . . There is here an infinity of an infinitely happy life to gain, a chance of gain against a finite number of chances of loss, and what you stake is finite. And so our proposition is of infinite force, when there is the finite to stake in a game where there are equal risks of gain and of loss, and the infinite to gain.
Probability theory arrived as a fully fledged area of mathematics in 1713 when Jacob Bernoulli published his Ars Conjectandi (‘Art of Conjecturing’). He started with the usual working definition of the probability of an event: the proportion of occasions on which it will happen, in the long run, nearly all the time. I say ‘working definition’ because this approach to probabilities runs into trouble if you try to make it fundamental. For example, suppose that I have a fair coin and keep tossing it. Most of the time I get a random-looking sequence of heads and tails, and if I keep tossing for long enough I will get heads roughly half the time. However, I seldom get heads exactly half the time: this is impossible on odd-numbered tosses, for example. If I try to modify the definition by taking inspiration from calculus, so that the probability of throwing heads is the limit of the proportion of heads as the number of tosses tends to infinity, I have to prove that this limit exists. But sometimes it doesn’t. For example, suppose that the sequence of heads and tails goes
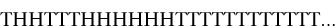
with one tail, two heads, three tails, six heads, twelve tails, and so on – the numbers doubling at each stage after the three tails. After three tosses the proportion of heads is 2/3, after six tosses it is 1/3, after twelve tosses it is back to 2/3, after twenty-four it is 1/3,. . . so the proportion oscillates to and fro, between 2/3 and 1/3, and therefore has no well-defined limit.
Agreed, such a sequence of tosses is very unlikely, but to define ‘unlikely’ we need to define probability, which is what the limit is supposed to achieve. So the logic is circular. Moreover, even if the limit exists, it might not be the ‘correct’ value of 1/2. An extreme case occurs when the coin always lands heads. Now the limit is 1. Again, this is wildly improbable, but. . .
Bernoulli decided to approach the whole issue from the opposite direction. Start by simply defining the probability of heads and tails to be some number p between 0 and 1. Say that the coin is fair if p = 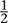 , and biased if not. Now Bernoulli proves a basic theorem, the law of large numbers. Introduce a reasonable rule for assigning probabilities to a series of repeated events. The law of large numbers states that in the long run, with the exception of a fraction of trials that becomes arbitrarily small, the proportion of heads does have a limit, and that limit is p. Philosophically, this theorem shows that by assigning probabilities – that is, numbers – in a natural way, the interpretation ‘proportion of occurrences in the long run, ignoring rare exceptions’ is valid. So Bernoulli takes the point of view that the numbers assigned as probabilities provide a consistent mathematical model of the process of tossing a coin over and over again.
, and biased if not. Now Bernoulli proves a basic theorem, the law of large numbers. Introduce a reasonable rule for assigning probabilities to a series of repeated events. The law of large numbers states that in the long run, with the exception of a fraction of trials that becomes arbitrarily small, the proportion of heads does have a limit, and that limit is p. Philosophically, this theorem shows that by assigning probabilities – that is, numbers – in a natural way, the interpretation ‘proportion of occurrences in the long run, ignoring rare exceptions’ is valid. So Bernoulli takes the point of view that the numbers assigned as probabilities provide a consistent mathematical model of the process of tossing a coin over and over again.
His proof depends on a numerical pattern that was very familiar to Pascal. It is usually called Pascal’s triangle, even though he wasn’t the first person to notice it. Historians have traced its origins back to the Chandas Shastra, a Sanskit text attributed to Pingala, written some time between 500 BC and 200 BC. The original has not survived, but the work is known through tenth-century Hindu commentaries. Pascal’s triangle looks like this:

where all rows start and end in 1, and each number is the sum of the two immediately above it. We now call these numbers binomial coefficients, because they arise in the algebra of the binomial (two-variable) expression (p + q)n. Namely,
(p + q)0 = 1
(p + q)1 = p + q
(p + q)2 = p2 + 2pq + q2
(p + q)3 = p3 + 3p2q + 3pq2 + q3
(p + q)4 = p4 + 4p3q + 6p2q2 + 4pq3 + q4
and Pascal’s triangle is visible as the coefficients of the separate terms.
Bernoulli’s key insight is that if we toss a coin n times, with a probability p of getting heads, then the probability of a specific number of tosses yielding heads is the corresponding term of (p + q)n, where q = 1 − p. For example, suppose that I toss the coin three times. Then the eight possible results are:
HHH |
|
|
HHT |
HTH |
THH |
HTT |
THT |
TTH |
TTT |
|
|
where I’ve grouped the sequences according to the number of heads. So out of the eight possible sequences, there are
1 sequence with 3 heads
3 sequences with 2 heads
3 sequences with 1 heads
1 sequence with 0 heads
The link with binomial coefficients is no coincidence. If you expand the algebraic formula (H + T)3 but don’t collect the terms together, you get
HHH + HHT + HTH + THH + HTT + THT + TTH + TTT
Collecting terms according to the number of Hs then gives
H3 + 3H2T + 3HT2+T3
After that, it’s a matter of replacing each of H and T by its probability, p or q respectively.
Even in this case, each extreme HHH and TTT occurs only once in eight trials, and more equitable numbers occur in the other six. A more sophisticated calculation using standard properties of binomial coefficients proves Bernoulli’s law of large numbers.
Advances in mathematics often come about because of ignorance. When mathematicians don’t know how to calculate something important, they find a way to sneak up on it indirectly. In this case, the problem is to calculate those binomial coefficients. There’s an explicit formula, but if, for instance, you want to know the probability of getting exactly 42 heads when tossing a coin 100 times, you have to do 200 multiplications and then simplify a very complicated fraction. (There are short cuts; it’s still a big mess.) My computer tells me in a split second that the answer is
28, 258, 808, 871, 162, 574, 166, 368, 460, 400 p42 q58
but Bernoulli didn’t have that luxury. No one did until the 1960s, and computer algebra systems didn’t really become widely available until the late 1980s.
Since this kind of direct calculation wasn’t feasible, Bernoulli’s immediate successors tried to find good approximations. Around 1730 Abraham De Moivre derived an approximate formula for the probabilities involved in repeated tosses of a biased coin. This led to the error function or normal distribution, often referred to as the ‘bell curve’ because of its shape. What he proved was this. Define the normal distribution Φ(x) with mean μ and variance σ2 by the formula
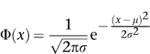
Then for large n the probability of getting m heads in n tosses of a biased coin is very close to Φ(x) when
x = m/n − p μ = np σ = npq
Here ‘mean’ refers to the average, and ‘variance’ is a measure of how far the data spread out – the width of the bell curve. The square root of the variance, σ itself, is called the standard deviation. Figure 32 (left) shows how the value of Φx depends on x. The curve looks a bit like a bell, hence the informal name. The bell curve is an example of a probability distribution; this means that the probability of obtaining data between two given values is equal to the area under the curve and between the vertical lines corresponding to those values. The total area under the curve is 1, thanks to that unexpected factor 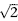
The idea is most easily grasped using an example. Figure 32 (right) shows a graph of the probabilities of getting various numbers of heads when tossing a fair coin 15 times (rectangular bars) together with the approximating bell curve.
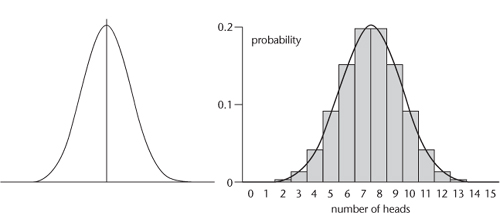
Fig 32 Left: Bell curve. right: How it approximates the number of heads in 15 tosses of a fair coin.
The bell curve began to acquire iconic status when it started showing up in empirical data in the social sciences, not just theoretical mathematics. In 1835 Adolphe Quetelet, a Belgian who among other things pioneered quantitative methods in sociology, collected and analysed large quantities of data on crime, the divorce rate, suicide, births, deaths, human height, weight, and so on – variables that no one expected to conform to any mathematical law, because their underlying causes were too complex and involved human choices. Consider, for example, the emotional torment that drives someone to commit suicide. It seemed ridiculous to think that this could be reduced to a simple formula.
These objections make good sense if you want to predict exactly who will kill themselves, and when. But when Quetelet concentrated on statistical questions, such as the proportion of suicides in various groups of people, various locations, and different years, he started to see patterns. These proved controversial: if you predict that there will be six suicides in Paris next year, how can this make sense when each person involved has free will? They could all change their minds. But the population formed by those who do kill themselves is not specified beforehand; it comes together as a consequence of choices made not just by those who commit suicide, but by those who thought about it and didn’t. People exercise free will in the context of many other things, which influence what they freely decide: here the constraints include financial problems, relationship problems, mental state, religious background. . . In any case, the bell curve does not make exact predictions; it just states which figure is most likely. Five or seven suicides might occur, leaving plenty of room for anyone to exercise free will and change their mind.
The data eventually won the day: for whatever reason, people en masse behaved more predictably than individuals. Perhaps the simplest example was height. When Quetelet plotted the proportions of people with a given height, he obtained a beautiful bell curve, Figure 33. He got the same shape of curve for many other social variables.
Quetelet was so struck by his results that he wrote a book, Sur l’homme et le développement de ses facultés (‘1Treatise on Man and the Development of His Faculties’) published in 1835. In it, he introduced the notion of the ‘average man’, a fictitious individual who was in every respect average. It has long been noted that this doesn’t entirely work: the average ‘man’ – that is, person, so the calculation includes males and females – has (slightly less than) one breast, one testicle, 2.3 children, and so on. Nevertheless Quetelet viewed his average man as the goal of social justice, not just a suggestive mathematical fiction. It’s not quite as absurd as it sounds. For example, if human wealth is spread equally to all, then everyone will have average wealth. It’s not a practical goal, barring enormous social changes, but someone with strong egalitarian views might defend it as a desirable target.
Fig 33 Quetelet’s graph of how many people (vertical axis) have a given height (horizontal axis).
The bell curve rapidly became an icon in probability theory, especially its applied arm, statistics. There were two main reasons: the bell curve was relatively simple to calculate, and there was a theoretical reason for it to occur in practice. One of the main sources for this way of thinking was eighteenth-century astronomy. Observational data are subject to errors, caused by slight variations in apparatus, human mistakes, or merely the movement of air currents in the atmosphere. Astronomers of the period wanted to observe planets, comets, and asteroids, and calculate their orbits, and this required finding whichever orbit fitted the data best. The fit would never be perfect.
The practical solution to this problem appeared first. It boiled down to this: run a straight line through the data, and choose this line so that the total error is as small as possible. Errors here have to be considered positive, and the easy way to achieve this while keeping the algebra nice is to square them. So the total error is the sum of the squares of the deviations of observations from the straight line model, and the desired line minimises this. In 1805 the French mathematician Adrien-Marie Legendre discovered a simple formula for this line, making it easy to calculate. The result is called the method of least squares. Figure 34 illustrates the method on artificial data relating stress (measured by a questionnaire) and blood pressure. The line in the figure, found using Legendre’s formula, fits the data most closely according to the squared-error measure. Within ten years the method of least squares was standard among astronomers in France, Prussia, and Italy. Within another twenty years it was standard in England.
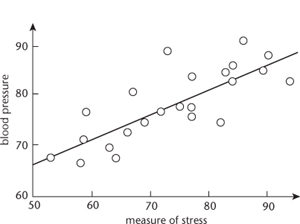
Fig 34 Using the method of least squares to relate blood pressure and stress. Dots: data. Solid line: best-fitting straight line.
Gauss made the method of least squares a cornerstone of his work in celestial mechanics. He got into the area in 1801 by successfully predicting the return of the asteroid Ceres after it was hidden in the glare of the Sun, when most astronomers thought the available data were too limited. This triumph sealed his mathematical reputation among the public and set him up for life as professor of astronomy at the University of Göttingen. Gauss didn’t use least squares for this particular prediction: his calculations boiled down to solving an algebraic equation of the eighth degree, which he did by a specially invented numerical method. But in his later work, culminating in his 1809 Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientum (‘Theory of Motion of the Celestial Bodies Moving in Conic Sections around the Sun’) he placed great emphasis on the method of least squares. He also stated that he had developed the idea, and used it, ten years before Legendre, which caused a bit of a fuss. It was very likely true, however, and Gauss’s justification of the method was quite different. Legendre had viewed it as an exercise in curve-fitting, whereas Gauss saw it as a way to fit a probability distribution. His justification of the formula assumed that the underlying data, to which the straight line was being fitted, followed a bell curve.
It remained to justify the justification. Why should observational errors be normally distributed? In 1810 Laplace supplied an astonishing answer, also motivated by astronomy. In many branches of science it is standard to make the same observation several times, independently, and then take the average. So it is natural to model this procedure mathematically. Laplace used the Fourier transform, see Chapter 9, to prove that the average of many observations is described by a bell curve, even if the individual observations are not. His result, the central limit theorem, was a major turning point in probability and statistics, because it provided a theoretical justification for using the mathematicians’ favourite distribution, the bell curve, in the analysis of observational errors.3
The central limit theorem singled out the bell curve as the probability distribution uniquely suited to the mean of many repeated observations. It therefore acquired the name ‘normal distribution’, and was seen as the default choice for a probability distribution. Not only did the normal distribution have pleasant mathematical properties, but there was also a solid reason for assuming it modelled real data. This combination of attributes proved very attractive to scientists wishing to gain insights into the social phenomena that had interested Quetelet, because it offered a way to analyse data from official records. In 1865 Francis Galton studied how a child’s height relates to its parents’ heights. This was part of a wider goal: understanding heredity – how human characteristics pass from parent to child. Ironically, Laplace’s central limit theorem initially led Galton to doubt that this kind of inheritance existed. And, even if it did, proving that would be difficult, because the central limit theorem was a double-edged sword. Quetelet had found a beautiful bell curve for heights, but that seemed to imply very little about the different factors that affected height, because the central limit theorem predicted a normal distribution anyway, whatever the distributions of those factors might be. Even if characteristics of the parents were among those factors, they might be overwhelmed by all the others – such as nutrition, health, social status, and so on.
By 1889, however, Galton had found a way out of this dilemma. The proof of Laplace’s wonderful theorem relied on averaging out the effects of many distinct factors, but these had to satisfy some stringent conditions. In 1875 Galton described these conditions as ‘highly artificial’, and noted that the influences being averaged
must be (1) all independent in their effects, (2) all equal [having the same probability distribution], (3) all admitting of being treated as simple alternatives ‘above average’ or ‘below average’; and (4) . . . calculated on the supposition that the variable influences are infinitely numerous.
None of these conditions applied to human heredity. Condition (4) corresponds to Laplace’s assumption that the number of factors being added tends to infinity, so ‘infinitely numerous’ is a bit of an exaggeration; however, what the mathematics established was that to get a good approximation to a normal distribution, you had to combine a large number of factors. Each of these contributed a small amount to the average: with, say, a hundred factors, each contributed one hundredth of its value. Galton referred to such factors as ‘petty’. Each on its own had no significant effect.
There was a potential way out, and Galton seized on it. The central limit theorem provided a sufficient condition for a distribution to be normal, not a necessary one. Even when its assumptions failed, the distribution concerned might still be normal for other reasons. Galton’s task was to find out what those reasons might be. To have any hope of linking to heredity, they had to apply to a combination of a few large and disparate influences, not to a huge number of insignificant influences. He slowly groped his way towards a solution, and found it through two experiments, both dating to 1877. One was a device he called a quincunx, in which ball bearings fell down a slope, bouncing off an array of pins, with an equal chance of going left or right. In theory the balls should pile up at the bottom according to a binomial distribution, a discrete approximation to the normal distribution, so they should – and did – form a roughly bellshaped heap, like Figure 32 (right). His key insight was to imagine temporarily halting the balls when they were part way down. They would still form a bell curve, but it would be narrower than the final one. Imagine releasing just one compartment of balls. It would fall to the bottom, spreading out into a tiny bell curve. The same went for any other compartment. And that meant that the final, large bell curve could be viewed as a sum of lots of tiny ones. The bell curve reproduces itself when several factors, each following its own separate bell curve, are combined.
The clincher arrived when Galton bred sweet peas. In 1875 he distributed seeds to seven friends. Each received 70 seeds, but one received very light seeds, one slightly heavier ones, and so on. In 1877 he measured the weights of the seeds of the resulting progeny. Each group was normally distributed, but the mean weight differed in each case, being comparable to the weight of each seed in the original group. When he combined the data for all of the groups, the results were again normally distributed, but the variance was bigger – the bell curve was wider. Again, this suggested that combining several bell curves led to another bell curve. Galton tracked down the mathematical reason for this. Suppose that two random variables are normally distributed, not necessarily with the same means or the same variances. Then their sum is also normally distributed; its mean is the sum of the two means, and its variance is the sum of the two variances. Obviously the same goes for sums of three, four, or more normally distributed random variables.
This theorem works when a small number of factors are combined, and each factor can be multiplied by a constant, so it actually works for any linear combination. The normal distribution is valid even when the effect of each factor is large. Now Galton could see how this result applied to heredity. Suppose that the random variable given by the height of a child is some combination of the corresponding random variables for the heights of its parents, and these are normally distributed. Assuming that the hereditary factors work by addition, the child’s height will also be normally distributed.
Galton wrote his ideas up in 1889 under the title Natural Inheritance. In particular, he discussed an idea he called regression. When one tall parent and one short one have children, the mean height of the children should be intermediate – in fact, it should be the average of the parents’ heights. The variance likewise should be the average of the variances, but the variances for the parents seemed to be roughly equal, so the variance didn’t change much. As successive generations passed, the mean height would ‘regress’ to a fixed middle-of-the-road value, while the variance would stay pretty much unchanged. So Quetelet’s neat bell curve could survive from one generation to the next. Its peak would quickly settle to a fixed value, the overall mean, while its width would stay the same. So each generation would have the same diversity of heights, despite regression to the mean. Diversity would be maintained by rare individuals who failed to regress and was self-sustaining in a sufficiently large population.
With the central role of the bell curve firmly cemented to what at the time were considered solid foundations, statisticians could build on Galton’s insights and workers in other fields could apply the results. Social science was an early beneficiary, but biology soon followed, and the physical sciences were already ahead of the game thanks to Legendre, Laplace, and Gauss. Soon an entire statistical toolbox was available for anyone who wanted to extract patterns from data. I’ll focus on just one technique, because it is routinely used to determine the efficacy of drugs and medical procedures, along with many other applications. It is called hypothesis testing, and its goal is to assess the significance of apparent patterns in data. It was founded by four people: the Englishmen Ronald Aylmer Fisher, Karl Pearson, and his son Egon, together with a Russian-born Pole who spent most of his life in America, Jerzy Neyman. I’ll concentrate on Fisher, who developed the basic ideas when working as an agricultural statistician at Rothamstead Experimental Station, analysing new breeds of plants.
Suppose you are breeding a new variety of potato. Your data suggest that this breed is more resistant to some pest. But all such data are subject to many sources of error, so you can’t be fully confident that the numbers support that conclusion – certainly not as confident as a physicist who can make very precise measurements and eliminate most errors. Fisher realised that the key issue is to distinguish a genuine difference from one arising purely by chance, and that the way to do this is to ask how probable that difference would be if only chance were involved.
Assume, for instance, that the new breed of potato appears to confer twice as much resistance, in the sense that the proportion of the new breed that survives the pest is double the proportion for the old breed. It is conceivable that this effect is due to chance, and you can calculate its probability. In fact, what you calculate is the probability of a result at least as extreme as the one observed in the data. What is the probability that the proportion of the new breed that survives the pest is at least twice what it was for the old breed? Even larger proportions are permitted here because the probability of getting exactly twice the proportion is bound to be very small. The wider the range of results you include, the more probable the effects of chance become, so you can have greater confidence in your conclusion if your calculation suggests it is not the result of chance. If this probability derived by this calculation is low, say 0.05, then the result is unlikely to be the result of chance; it is said to be significant at the 95% level. If the probability is lower, say 0.01, then the result is extremely unlikely to be the result of chance, and it is said to be significant at the 99% level. The percentages indicate that by chance alone, the result would not be as extreme as the one observed in 95% of trials, or in 99% of them.
Fisher described his method as a comparison between two distinct hypotheses: the hypothesis that the data are significant at the stated level, and the so-called null hypothesis that the results are due to chance. He insisted that his method must not be interpreted as confirming the hypothesis that the data are significant; it should be interpreted as a rejection of the null hypothesis. That is, it provides evidence against the data not being significant.
This may seem a very fine distinction, since evidence against the data not being significant surely counts as evidence in favour of it being significant. However, that’s not entirely true, and the reason is that the null hypothesis has an extra built-in assumption. In order to calculate the probability that a result at least as extreme is due to chance, you need a theoretical model. The simplest way to get one is to assume a specific probability distribution. This assumption applies only in connection with the null hypothesis, because that’s what you use to do the sums. You don’t assume the data are normally distributed. But the default distribution for the null hypothesis is normal: the bell curve.
This built-in model has an important consequence, which ‘reject the null hypothesis’ tends to conceal. The null hypothesis is ‘the data are due to chance’. So it is all too easy to read that statement as ‘reject the data being due to chance’, which in turn means you accept that they’re not due to chance. Actually, though, the null hypothesis is ‘the data are due to chance and the effects of chance are normally distributed’, so there might be two reasons to reject the null hypothesis: the data are not due to chance, or they are not normally distributed. The first supports the significance of the data, but the second does not. It says you might be using the wrong statistical model.
In Fisher’s agricultural work, there was generally plenty of evidence for normal distributions in the data. So the distinction I’m making didn’t really matter. In other applications of hypothesis testing, though, it might. Saying that the calculations reject the null hypothesis has the virtue of being true, but because the assumption of a normal distribution is not explicitly mentioned, it is all too easy to forget that you need to check normality of the distribution of the data before you conclude that your results are statistically significant. As the method gets used by more and more people, who have been trained in how to do the sums but not in the assumptions behind them, there is a growing danger of wrongly assuming that the test shows your data to be significant. Especially when the normal distribution has become the automatic default assumption.
In the public consciousness, the term ‘bell curve’ is indelibly associated with the controversial 1994 book The Bell Curve by two Americans, the psychologist Richard J. Herrnstein and the political scientist Charles Murray. The main theme of the book is a claimed link between intelligence, measured by intelligence quotient (IQ), and social variables such as income, employment, pregnancy rates, and crime. The authors argue that IQ levels are better at predicting such variables than the social and economic status of the parents or their level of education. The reasons for the controversy, and the arguments involved, are complex. A quick sketch cannot really do justice to the debate, but the issues go right back to Quetelet and deserve mention.
Controversy was inevitable, no matter what the academic merits or demerits of the book might have been, because it touched a sensitive nerve: the relation between race and intelligence. Media reports tended to stress the proposal that differences in IQ have a predominantly genetic origin, but the book was more cautious about this link, leaving the interaction between genes, environment, and intelligence open. Another controversial issue was an analysis suggesting that social stratification in the United States (and indeed elsewhere) increased significantly throughout the twentieth century, and that the main cause was differences in intelligence. Yet another was a series of policy recommendations for dealing with this alleged problem. One was to reduce immigration, which the book claimed was lowering average IQ. Perhaps the most contentious was the suggestion that social welfare policies allegedly encouraging poor women to have children should be stopped.
Ironically, this idea goes back to Galton himself. His 1869 book Hereditary Genius built on earlier writings to develop the idea that ‘a man’s natural abilities are derived by inheritance, under exactly the same limitations as are the form and physical features of the whole organic world. Consequently . . . it would be quite practicable to produce a highly-gifted race of men by judicious marriages during several consecutive generations.’ He asserted that fertility was higher among the less intelligent, but avoided any suggestion of deliberate selection in favour of intelligence. Instead, he expressed the hope that society might change so that the more intelligent people understood the need to have plenty of children.
To many, Herrnstein and Murray’s proposal to re-engineer the welfare system was uncomfortably close to the eugenics movement of the early twentieth century, in which 60,000 Americans were sterilised, allegedly because of mental illness. Eugenics became widely discredited when it became associated with Nazi Germany and the holocaust, and many of its practices are now considered to be violations of human rights legislation, in some cases amounting to crimes against humanity. Proposals to breed humans selectively are widely viewed as inherently racist. A number of social scientists endorsed the book’s scientific conclusions but disputed the charge of racism; some of them were less sure about the policy proposals.
The Bell Curve initiated a lengthy debate about the methods used to compile data, the mathematical methods used to analyse them, the interpretation of the results, and the policy suggestions based on those interpretations. A task force set up by the American Psychological Association concluded that some points made in the book are valid: IQ scores are good for predicting academic achievement, this correlates with employment status, and there is no significant difference in the performance of males and females. On the other hand, the task force’s report reaffirmed that both genes and environment influence IQ and it found no significant evidence that racial differences in IQ scores are genetically determined.
Other critics have argued that there are flaws in the scientific methodology, such as inconvenient data being ignored, and that the study and some responses to it may to some extent have been politically motivated. For example, it is true that social stratification has increased dramatically in the United States, but it could be argued that the main cause is the refusal of the rich to pay taxes, rather than differences in intelligence. There also seems to be an inconsistency between the alleged problem and the proposed solution. If poverty causes people to have more children, and you believe that this is a bad thing, why on earth would you want to make them even poorer?
An important part of the background, often ignored, is the definition of IQ. Rather than being something directly measurable, such as height or weight, IQ is inferred statistically from tests. Subjects are set questions, and their scores are analysed using an offshoot of the method of least squares called analysis of variance. Like the method of least squares, this technique assumes that the data are normally distributed, and it seeks to isolate those factors that determine the largest amount of variability in the data, and are therefore the most important for modelling the data. In 1904 the psychologist Charles Spearman applied this technique to several different intelligence tests. He observed that the scores that subjects obtained on different tests were highly correlated; that is, if someone did well on one test, they tended to do well on them all. Intuitively, they seemed to be measuring the same thing. Spearman’s analysis showed that a single common factor – one mathematical variable, which he called g, standing for ‘general intelligence’ – explained almost all of the correlation. IQ is a standardised version of Spearman’s g.
A key question is whether g is a real quantity or a mathematical fiction.
The answer is complicated by the methods used to choose IQ tests. These assume that the ‘correct’ distribution of intelligence in the population is normal – the eponymous bell curve – and calibrate the tests by manipulating scores mathematically to standardise the mean and standard deviation. A potential danger here is that you get what you expect because you take steps to filter out anything that would contradict it. Stephen Jay Gould made an extensive critique of such dangers in 1981 in The Mismeasure of Man, pointing out among other things that raw scores on IQ tests are often not normally distributed at all.
The main reason for thinking that g represents a genuine feature of human intelligence is that it is one factor: mathematically, it defines a single dimension. If many different tests all seem to be measuring the same thing, it is tempting to conclude that the thing concerned must be real. If not, why would the results all be so similar? Part of the answer could be that the results of IQ tests are reduced to a single numerical score. This squashes a multidimensional set of questions and potential attitudes down to a one-dimensional answer. Moreover, the test has been selected so that the score correlates strongly with the designer’s view of intelligent answers – if not, no one would consider using it.
By analogy, imagine collecting data on several different aspects of ‘size’ in the animal kingdom. One might measure mass, another height, others length, width, diameter of left hind leg, tooth size, and so on. Each such measure would be a single number. They would in general be closely correlated: tall animals tend to weight more, have bigger teeth, thicker legs. . . If you ran the data through an analysis of variance you would very probably find that a single combination of those data accounted for the vast majority of the variability, just like Spearman’s g does for different measurements of things thought to relate to intelligence. Would this necessarily imply that all of these features of animals have the same underlying cause? That one thing controls them all? Possibly: a growth hormone level, perhaps? But probably not. The richness of animal form does not comfortably compress into a single number. Many other features do not correlate with size at all: ability to fly, being striped or spotted, eating flesh or vegetation. The single special combination of measurements that accounts for most of the variability could be a mathematical consequence of the methods used to find it – especially if those variables were chosen, as here, to have a lot in common to begin with.
Going back to Spearman, we see that his much-vaunted g may be one-dimensional because IQ tests are one-dimensional. IQ is a statistical method for quantifying specific kinds of problem-solving ability, mathematically convenient but not necessarily corresponding to a real attribute of the human brain, and not necessarily representing whatever it is that we mean by ‘intelligence’.
By focusing on one issue, IQ, and using that to set policy, The Bell Curve ignores the wider context. Even if it were sensible to genetically engineer a nation’s population, why confine the process to the poor? Even if on average the poor have lower IQs than the rich, a bright poor child will outperform a dumb rich one any day, despite the obvious social and educational advantages that children of the rich enjoy. Why resort to welfare cuts when you could aim more accurately at what you claim to be the real problem: intelligence itself? Why not improve education? Indeed, why aim your policy at increasing intelligence at all? There are many other desirable human traits. Why not reduce gullibility, aggressiveness, or greed?
It is a mistake to think about a mathematical model as if it were the reality. In the physical sciences, where the model often fits reality very well, this may be a convenient way of thinking that causes little harm. But in the social sciences, models are often little better than caricatures. The choice of title for The Bell Curve hints at this tendency to conflate model with reality. The idea that IQ is some sort of precise measure of human ability, merely because it has a mathematical pedigree, makes the same error. It is not sensible to base sweeping and highly contentious social policy on simplistic, flawed mathematical models. The real point about The Bell Curve, one that it makes extensively but inadvertently, is that cleverness, intelligence, and wisdom are not the same.
Probability theory is widely used in medical trials of new drugs and treatments to test the statistical significance of data. The tests are often, but not always, based on the assumption that the underlying distribution is normal. A typical example is the detection of cancer clusters. A cluster, for some disease, is a group within which the disease occurs more frequently than expected in the overall population. The cluster may be geographical, or it may refer more metaphorically to people with a particular lifestyle, or a specific period of time. For example, retired professional wrestlers, or boys born between 1960 and 1970.
Apparent clusters may be due entirely to chance. Random numbers are seldom spread out in a roughly uniform way; instead, they often cluster together. In random simulations of the UK National Lottery, where six numbers between 1 and 49 are randomly drawn, more than half appear to show some kind of regular pattern such as two numbers being consecutive or three numbers separated by the same amount, for example 5, 9, 13. Contrary to common intuition, random is clumped. When an apparent cluster is found, the medical authorities try to assess whether it is due to chance or whether there might be some possible causal connection. At one time, most children of Israeli fighter pilots were boys. It would be easy to think of possible explanations – pilots are very virile and virile men sire more boys (not true, by the way), pilots are exposed to more radiation than normal, they experience higher g-forces – but this phenomenon was short-lived, just a random cluster. In later data it disappeared. In any population of people, it is always likely that there will be more children of one sex or the other; exact equality is very improbable. To assess the significance of the cluster, you should keep observing and see whether it persists.
However, this procrastination can’t be continued indefinitely, especially if the cluster involves a serious disease. AIDS was first detected as a cluster of pneumonia cases in American homosexual men in the 1980s, for instance. Asbestos fibres as a cause of a form of lung cancer, mesothelioma, first showed up as a cluster among former asbestos workers. So statistical methods are used to assess how probable such a cluster would be if it arose for random reasons. Fisher’s methods of significance testing, and related methods, are widely used for that purpose.
Probability theory is also fundamental to our understanding of risk. This word has a specific, technical meaning. It refers to the potential for some action to lead to an undesirable outcome. For example, flying in an aircraft could result in being involved in a crash, smoking cigarettes could lead to lung cancer, building a nuclear power station could lead to the release of radiation in an accident or a terrorist attack, building a dam for hydroelectric power could cause deaths if the dam collapses. ‘Action’ here can refer to not doing something: failing to vaccinate a child might lead to its death from a disease, for example. In this case there is also a risk associated with vaccinating the child, such as an allergic reaction. Over the whole population this risk is smaller, but for specific groups it can be larger.
Many different concepts of risk are employed in different contexts. The usual mathematical definition is that the risk associated with some action or inaction is the probability of an adverse result, multiplied by the loss that would then be incurred. By this definition a one in ten chance of killing ten people has the same level of risk as a one in a million chance of killing a million people. The mathematical definition is rational in the sense that there is a specific rationale behind it, but that doesn’t mean that it is necessarily sensible. We’ve already seen that ‘probability’ refers to the long run, but for rare events the long run is very long indeed. Humans, and their societies, can adapt to repeated small numbers of deaths, but a country that suddenly lost a million people at once would be in serious trouble, because all public services and industry would simultaneously come under a severe strain. It would be little comfort to be told that over the next 10 million years, the total deaths in the two cases would be comparable. So new methods are being developed to quantify risk in such cases.
Statistical methods, derived from questions about gambling, have a huge variety of uses. They provide tools for analysing social, medical, and scientific data. Like all tools, what happens depends on how they are used. Anyone using statistical methods needs to be aware of the assumptions behind those methods, and their implications. Blindly feeding numbers into a computer and taking the results as gospel, without understanding the limitations of the method being used, is a recipe for disaster. The legitimate use of statistics, however, has improved our world out of all recognition. And it all began with Quetelet’s bell curve.