Newton’s laws of motion capture the relationship between the forces that act on a body and how it moves in response to those forces. Calculus provides mathematical techniques for solving the resulting equations. One further ingredient is needed to apply the laws: specifying the forces. The most ambitious aspect of Newton’s Principia was to do precisely that for the bodies of the Solar System – the Sun, planets, moons, asteroids, and comets. Newton’s law of gravitation synthesised, in one simple mathematical formula, millennia of astronomical observations and theories. It explained many puzzling features of planetary motion, and made it possible to predict the future movements of the Solar System with great accuracy. Einstein’s theory of general relativity eventually superseded the Newtonian theory of gravity, as far as fundamental physics is concerned, but for almost all practical purposes the simpler Newtonian approach still reigns supreme. Today the world’s space agencies, such as NASA and ESA, still use Newton’s laws of motion and gravitation to work out the most effective trajectories for spacecraft.
It was Newton’s law of gravitation, above all else, that justified his subtitle: The System of the World. This law demonstrated the enormous power of mathematics to find hidden patterns in nature and to reveal hidden simplicities behind the world’s complexities. And in time, as mathematicians and astronomers asked harder questions, to reveal the hidden complexities implicit in Newton’s simple law. To appreciate what Newton achieved, we must first go back in time, to see how previous cultures viewed the stars and planets.
Humans have been watching the night sky since the dawn of history. Their initial impression would have been a random scattering of bright points of light, but they would soon have noticed that across this background the glowing orb of the Moon traced a regular path, changing shape as it did so. They would also have seen that most of those tiny bright specks of light remain in the same relative patterns, which we now call constellations. Stars move across the night sky, but they move as a single rigid unit, as if the constellations are painted on the inside of a gigantic, rotating bowl.1 However, a small number of stars behave quite differently: they seem to wander around the sky. Their paths are quite complicated, and some appear to loop back on themselves from time to time. These are the planets, a word that comes from the Greek for ‘wanderer’. The ancients recognised five of them, now called Mercury, Venus, Mars, Jupiter, and Saturn. They move relative to the fixed stars at different speeds, with Saturn being the slowest.
Other celestial phenomena were even more puzzling. From time to time a comet would appear, as if from nowhere, trailing a long, curved tail. ‘Shooting stars’ would seem to fall from the heavens, as if they had become detached from their supporting bowl. It is no wonder that early humans attributed the irregularities of the heavens to the caprices of supernatural beings.
The regularities could be summed up in terms so obvious that few would ever dream of disputing them. The Sun, stars, and planets revolve around a stationary Earth. That’s what it looks like, that’s what it feels like, so that’s how it must be. To the ancients, the cosmos was geocentric – Earth-centred. One lone voice disputed the obvious: Aristarchus of Samos. Using geometrical principles and observations, Aristarchus calculated the sizes of the Earth, the Sun, and the Moon. Around 270 BC he put forward the first heliocentric theory: the Earth and planets revolve round the Sun. His theory quickly fell out of favour and was not revived for nearly 2000 years.
By the time of Ptolemy, a Roman who lived in Egypt around 120 AD, the planets had been tamed. Their movements were not capricious, but predictable. Ptolemy’s Almagest (‘Great Treatise’) proposed that we live in a geocentric universe in which everything literally revolves around humanity in complex combinations of circles called epicycles, supported by giant crystal spheres. His theory was wrong, but the motions that it predicted were sufficiently accurate for the errors to remain undetected for centuries. Ptolemy’s system had an additional philosophical attraction: it represented the cosmos in terms of perfect geometric figures – spheres and circles. It continued the Pythagorean tradition. In Europe, the Ptolemaic theory remained unchallenged for 1400 years.
While Europe dawdled, new scientific advances were being made elsewhere, especially in Arabia, China, and India. In 499 the Indian astronomer Aryabhata put forward a mathematical model of the Solar System in which the Earth spun on its axis and the periods of planetary orbits were stated relative to the position of the Sun. In the Islamic world, Alhazen wrote a stinging criticism of the Ptolemaic theory, though this was probably not focused on its geocentric nature. Around 1000 Abu Rayhan Biruni gave serious consideration to the possibility of a heliocentric Solar System, with the Earth spinning on its axis, but eventually plumped for the orthodoxy of the time, a stationary Earth. Around 1300, Najm al-Din al-Qazwini al-Katibi proposed a heliocentric theory, but soon changed his mind.
The big breakthrough came with the work of Nicolaus Copernicus, published in 1543 as De Revolutionibus Orbium Coelestium (‘On the Revolutions of the Celestial Spheres’). There is evidence, notably the occurrence of almost identical diagrams labelled with the same letters, to suggest that Copernicus was, to say the least, influenced by al-Katibi, but he went much further. He set out an explicitly heliocentric system, argued that it fitted the observations better and more economically than Ptolemy’s geocentric theory did, and laid out some of the philosophical implications. Paramount among them was the novel thought that humans were not at the centre of things. The Christian Church viewed this suggestion as contrary to doctrine and did its best to discourage it. Explicit heliocentrism was heresy.

It prevailed nevertheless, because the evidence was so strong. New and better heliocentric theories appeared. Then the spheres were thrown away altogether, in favour of a different shape from classical geometry: the ellipse. Ellipses are oval shapes, and indirect evidence suggests they were first studied in Greek geometry by Menaechmus around 350 BC, along with hyperbolas and parabolas, as sections of a cone, Figure 13. Euclid is said to have written four books on conic sections, though nothing has survived if he did, and Archimedes investigated some of their properties. Greek research on the topic reached its climax in about 240 BC with the eight-volume Conic Sections by Apollonius of Perga, who found a way to define these curves purely within a plane, avoiding the third dimension. However, the Pythagorean view that circles and spheres attained a higher degree of perfection than ellipses and other more complex curves persisted.
Ellipses cemented their role in astronomy around 1600, with the work of Kepler. His astronomical interests began in childhood; at the age of six he witnessed the great comet of 1577,2 and three years later he saw an eclipse of the Moon. At the University of Tübingen, Kepler showed great talent for mathematics and put it to profitable use casting horoscopes. In those days mathematics, astronomy, and astrology often went together. He combined a heady level of mysticism with a level-headed attention to mathematical detail. A typical example is his Mysterium Cosmographicum (‘The Cosmographic Mystery’), a spirited defence of the heliocentric system published in 1596. It combines a clear grasp of Copernicus’s theory with what to modern eyes is a very strange speculation relating the distances of the known planets from the Sun to the regular solids. For a long time Kepler regarded this discovery as one of his greatest, revealing the Creator’s plan for the universe. He saw his later researches, which we now consider to be far more significant, as mere elaborations of this basic plan. At the time, one advantage of the theory was that it explained why there were precisely six planets (Mercury through Saturn). Between these six orbits lie five gaps, one for each regular solid. With the discovery of Uranus and later Neptune and Pluto (until its recent demotion from planetary status) this feature quickly became a fatal flaw.
Kepler’s lasting contribution has its roots in his employment by Tycho Brahe. The two first met in 1600. After a two-month stay and a heated argument Kepler negotiated an acceptable salary. Following a spate of problems in his home city of Graz he moved to Prague, assisting Tycho in the analysis of his planetary observations, especially of Mars. When Tycho unexpectedly died in 1601 Kepler took over his employer’s position as imperial mathematician to Rudolph II. His primary role was casting imperial horoscopes, but he also had time to continue his analysis of the orbit of Mars. Following traditional epicyclic principles he refined his model to the point at which its errors, compared with observation, were usually a mere two minutes of arc, the typical error in the observations themselves. However, he didn’t stop there because sometimes the errors were bigger, up to eight minutes of arc.
His search eventually led him to two laws of planetary motion, published in Astronomia Nova (‘A New Astronomy’). For many years he had tried to fit the orbit of Mars to an ovoid – an egg-shaped curve, sharper at one end than the other – without success. Perhaps he expected the orbit to be more curved closer to the Sun. In 1605 it occurred to Kepler to try an ellipse, equally rounded at both ends, and to his surprise this did a much better job. He concluded that all planetary orbits are ellipses, his first law. His second law described how the planet moves along its orbit, stating that planets sweep out equal areas in equal times. The book appeared in 1609. Kepler then devoted much of his effort to preparing various astronomical tables, but he returned to the regularities of planetary orbits in 1619 in his Harmonices Mundi (‘The Harmony of the World’). This book had some ideas we now find strange, for example that the planets emit musical sounds as they roll round the Sun. But it also includes his third law: the squares of the orbital periods are proportional to the cubes of the distances from the Sun.
Kepler’s three laws were all but buried amid a mass of mysticism, religious symbolism, and philosophical speculation. But they represented a giant leap forward, leading Newton to one of the greatest scientific discoveries of all time.
Newton derived his law of gravity from Kepler’s three laws of planetary motion. It states that every particle in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them. In symbols,
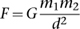
Here F is the attractive force, d is the distance, the ms are the two masses, and G is a specific number, the gravitational constant.3
Who discovered Newton’s law of gravity? It sounds like one of those self-answering questions, like ‘whose statue stands on top of Nelson’s column?’. But a reasonable answer is the curator of experiments at the Royal Society, Robert Hooke. When Newton published the law in 1687, in his Principia, Hooke accused him of plagiarism. However, Newton provided the first mathematical derivation of elliptical orbits from the law, which was vital in establishing its correctness, and Hooke acknowledged this. Moreover, Newton had cited Hooke, along with several others, in the book. Presumably Hooke felt he deserved more credit; he had suffered similar problems several times before and it was a sore point.
The idea that bodies attract each other had been floating around for a while, and so had its likely mathematical expression. In 1645 the French astronomer Ismaël Boulliau (Bullialdus) wrote his Astronomia Philolaica (‘Philolaic Astronomy’ – Philolaus was a Greek philosopher who thought that a central fire, not the Earth, was the centre of the universe). In it he wrote:
As for the power by which the Sun seizes or holds the planets, and which, being corporeal, functions in the manner of hands, it is emitted in straight lines throughout the whole extent of the world, and like the species of the Sun, it turns with the body of the Sun; now, seeing that it is corporeal, it becomes weaker and attenuated at a greater distance or interval, and the ratio of its decrease in strength is the same as in the case of light, namely, the duplicate proportion, but inversely, of the distances.
This is the famous ‘inverse square’ dependency of the force on distance. There are simple, though naive, reasons to expect such a formula, because the surface area of a sphere varies as the square of its radius. If the same amount of gravitational ‘stuff’ spreads out over ever-increasing spheres as it departs from the Sun, then the amount of it received at any point must vary in the inverse proportion to the surface area. Exactly this happens with light, and Boulliau assumed, without much evidence, that gravity must be analogous. He also thought that the planets move along their orbits under their own power, so to speak: ‘No kind of motion presses upon the remaining planets, [which] are driven round by individual forms with which they were provided.’
Hooke’s contribution dates to 1666, when he presented a paper to the Royal Society with the title ‘On gravity’. Here he sorted out what Boulliau had got wrong, arguing that an attractive force from the Sun could interfere with a planet’s natural tendency to move in a straight line (as specified by Newton’s third law of motion) and cause it to follow a curve. He also stated that ‘these attractive powers are so much the more powerful in operating, by how much the nearer the body wrought upon is to their own Centers’, showing that he thought the force fell off with distance. But he didn’t tell anyone else the mathematical form for this decrease until 1679, when he wrote to Newton: ‘The Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall.’ In the same letter he said that this implies that the velocity of a planet varies as the reciprocal of its distance from the Sun. Which is wrong.
When Hooke complained that Newton had stolen his law, Newton was having none of it, pointing out that he had discussed the idea with Christopher Wren before Hooke had sent his letter. To demonstrate prior art, he cited Boulliau, and also Giovanni Borelli, an Italian physiologist and mathematical physicist. Borelli had suggested that three forces combine to create planetary motion: an inward force caused by the planet’s desire to approach the Sun, a sideways force caused by sunlight, and an outward force caused by the Sun’s rotation. Score one out of three, and that’s generous.
Newton’s main point, generally considered decisive, is that whatever else Hooke had done, he had not deduced the exact form of orbits from inverse square law attraction. Newton had. In fact, he had deduced all three of Kepler’s laws of planetary motion: elliptical orbits, sweeping out equal areas in equal intervals of time, with the square of the period being proportional to the cube of the distance. ‘Without my Demonstrations,’ Newton insisted, the inverse square law ‘cannot be believed by a judicious philosopher to be anywhere accurate.’ But he did also accept that ‘Mr Hook is yet a stranger’ to this proof. A key feature of Newton’s argument is that it applies not just to a point particle, but to a sphere. This extension, which is crucial to planetary motion, had caused Newton considerable effort. His geometric proof is a disguised application of integral calculus, and he was justifiably proud of it. There is also documentary evidence that Newton had been thinking about such questions for quite a while.
At any rate, we name the law after Newton, and this does justice to the importance of his contribution.
The most important aspect of Newton’s law of gravitation is not the inverse square law as such. It is the assertion that gravitation acts universally. Any two bodies, anywhere in the universe, attract each other. Of course you need an accurate force law (inverse square) to get accurate results, but without universality, you don’t know how to write down the equations for any system with more than two bodies. Almost all of the interesting systems, such as the Solar System itself, or the fine structure of the motion of the Moon under the influence of (at least) the Sun and the Earth, involve more than two bodies, so Newton’s law would have been almost useless if it had applied only to the context in which he first deduced it.
What motivated this vision of universality? In his 1752 Memoirs of Sir Isaac Newton’s Life, William Stukeley reported a tale Newton had told him in 1726:
The notion of gravitation . . . was occasioned by the fall of an apple, as he sat in contemplative mood. Why should that apple always descend perpendicularly to the ground, thought he to himself. Why should it not go sideways or upwards, but constantly to the Earth’s centre? Assuredly the reason is, that the Earth draws it. There must be a drawing power in matter. And the sum of the drawing power in the matter of the Earth must be in the Earth’s centre, not in any side of the Earth. Therefore does this apple fall perpendicularly or towards the centre? If matter thus draws matter; it must be in proportion of its quantity. Therefore the apple draws the Earth, as well as the Earth draws the apple.
Whether the story is the literal truth, or a convenient fiction that Newton invented to help him explain his ideas later on, is not entirely clear, but it seems reasonable to take the tale at face value because the idea does not end with apples. The apple was important to Newton because it made him realise that the same law of forces can explain both the motion of the apple and that of the Moon. The only difference is that the Moon also moves sideways; this is why it stays up. Actually, it is always falling towards the Earth, but the sideways motion causes the Earth’s surface to fall away as well. Newton, being Newton, didn’t stop with this qualitative argument. He did the sums, compared them with observations, and was satisfied that his idea must be correct.
If gravity acts on the apple, the Moon, and the Earth, as an inherent feature of matter, then presumably it acts on everything.
It is not possible to verify the universality of gravitational forces directly; you would have to study all pairs of bodies in the entire universe, and find a way to remove the influence of all the other bodies. But that’s not how science works. Instead, it employs a mixture of inference and observations. Universality is a hypothesis, capable of being falsified every time it is applied. Every time it survives falsification – a fancy way to say it gives good results – the justification for using it becomes a little stronger. If (as in this case) it survives thousands of such tests, the justification becomes very strong indeed. However, the hypothesis can never be proved true: for all we know, the next experiment might produce incompatible results. Perhaps somewhere in a galaxy far, far away there is one speck of matter, one atom, that is not attracted to everything else. If so, we will never find it; equally, it won’t upset our calculations. The inverse square law itself is exceedingly difficult to verify directly, that is, by actually measuring the attractive force. Instead, we apply the law to systems that we can measure by using it to predict orbits, and then check whether the predictions agree with observations.
Even granting universality, it is not enough to write down an accurate law of attraction. That just produces an equation describing the motion. In order to find the motion itself, you have to solve the equation. Even for two bodies, this is not straightforward, and even bearing in mind that he knew in advance what answer to expect, Newton’s deduction of elliptical orbits is a tour de force. It explains why Kepler’s three laws provide a very accurate description of each planet’s orbit. It also explains why that description is not exact: other bodies in the solar system, other than the Sun and the planet itself, affect the motion. In order to account for these disturbances, you have to solve the equations of motion for three or more bodies. In particular, if you want to predict the motion of the Moon with high precision, you have to include the Sun and the Earth in your equations. The effects of the other planets, especially Jupiter, are not entirely negligible either, but they show up only in the long term. So, fresh from Newton’s success with the motion of two bodies under gravity, mathematicians and physicists moved on to the next case: three bodies. Their initial optimism dissipated rapidly: the three-body case turned out to be very different from the two-body case. In fact, it defied solution.
It was often possible to calculate good approximations to the motion (which often solved the problem for practical purposes), but there no longer seemed to be an exact formula. This problem bedevilled even simplified versions, such as the restricted three-body problem. Suppose that a planet orbits a star in a perfect circle: how will a speck of dust, of negligible mass, move?
Calculating approximate orbits for three or more bodies, by hand, using pencil and paper, was just about feasible, but very laborious. Mathematicians devised innumerable tricks and short cuts, leading to a reasonable understanding of several astronomical phenomena. Only in the late nineteenth century did the true complexity of the three-body problem become apparent, when Henri Poincaré realised that the geometry involved was necessarily extraordinarily intricate. And only in the late twentieth century did the advent of powerful computers reduce the labour of hand calculations, permitting accurate long-term predictions of the motion of the Solar System.
Poincaré’s breakthrough – if it can be called that, since at the time it seemed to be telling everyone that the problem was hopeless and it was pointless to seek a solution – came about because he competed for a mathematical prize. Oscar II, king of Sweden and Norway, announced a competition to celebrate his 60th birthday in 1889. Taking advice from the mathematician Gösta Mittag-Leffler, the king chose the general problem of arbitrarily many bodies moving under Newtonian gravitation. Since it was well understood that an explicit formula akin to the two-body ellipse was an unrealistic aim, the requirement was relaxed: the prize would be awarded for an approximation method of a very specific kind. Namely, the motion must be determined as an infinite series, giving results as accurate as we please if enough terms are included.
Poincaré did not answer this question. Instead, his memoir on the topic, published in 1890, provided evidence that it might not possess that kind of answer, even for just three bodies – star, planet, and dust particle. By thinking about the geometry of hypothetical solutions, Poincaré discovered that in some cases the orbit of the dust particle must be exceedingly complex and tangled. He then, in effect, threw up his hands in horror and made the pessimistic statement that ‘When one tries to depict the figure formed by these two curves and their infinity of intersections, each of which corresponds to a doubly asymptotic solution, these intersections form a kind of net, web or infinitely tight mesh. . . One is struck by the complexity of this figure that I am not even attempting to draw.’
We now see Poincaré’s work as a breakthrough, and discount his pessimism, because the complicated geometry that led him to despair of ever solving the problem actually provides powerful insights if it is properly developed and understood. The complex geometry of the associated dynamics turned out to be one of the earliest examples of chaos: the occurrence, in non-random equations, of solutions so complicated that in some respects they appear to be random, see Chapter 16.
There are several ironies in the story. Mathematical historian June Barrow-Green discovered that the published version of Poincaré’s prizewinning memoir was not the one that won the prize.4 This earlier version contained a major error, overlooking the chaotic solutions. The work was at proof stage when an embarrassed Poincaré realised his blunder, and he paid for a new printing of a corrected version. Almost all copies of the original were destroyed, but one remained tucked away in the archives of the Mittag-Leffler Institute in Sweden, where Barrow-Green found it.
It also turned out that the presence of chaos does not, in fact, rule out series solutions, but these are valid almost always rather than always. Karl Frithiof Sundman, a Finnish mathematician, discovered this in 1912 for the three-body problem, using series formed from powers of the cube root of time. (Powers of time won’t hack it.) The series converge – have a sensible sum – unless the initial state has zero angular momentum, but such states are infinitely rare, in the sense that a random choice of angular momentum is almost always nonzero. In 1991 the Chinese mathematician Qiudong Wang extended these results to any number of bodies, but did not classify the rare exceptions when the series fail to converge. Such a classification is likely to be very complicated: it must include solutions where bodies escape to infinity in finite time, or oscillate ever faster, both of which can happen for five or more bodies.
Newton’s law of gravity is routinely applied to design orbits for space missions. Here even two-body dynamics is useful in its own right. In its early days, the exploration of the Solar System mainly used two-body orbits, segments of ellipses. By burning its rockets the spacecraft could be switched from one ellipse to a different one. But as the aims of space programmes got more ambitious, more efficient methods were needed. They came from many-body dynamics, usually three bodies but occasionally as great as five. The new methods of chaos and topological dynamics became the basis of practical solutions to engineering problems.
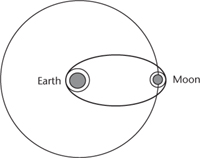
Fig 14 Hohmann transfer ellipse from low-Earth orbit to lunar orbit.
It all started with a simple question: What is the most efficient route from the Earth to the Moon or the planets? The classic answer, known as a Hohmann transfer ellipse (Figure 14), starts from a circular orbit round the Earth, and then follows part of a long, thin ellipse to join up with a second circular orbit round the destination. This method was employed for the Apollo missions of the 1960s and 1970s, but for many types of mission it has one disadvantage. The spacecraft must be boosted out of Earth orbit and slowed again to enter lunar orbit; this wastes fuel. There are alternatives involving many loops round the Earth, a transition through the point between Earth and Moon where their gravitational fields cancel, and many loops round the Moon. But trajectories like that take longer than Hohmann ellipses, so they were not used for the manned Apollo missions where food and oxygen, hence time, were of the essence. For unmanned missions, however, time is relatively cheap, whereas anything that adds to the overall weight of the spacecraft, including fuel, costs money.
By taking a fresh look at Newton’s law of gravity and his second law of motion, mathematicians and space engineers have recently discovered a new, and remarkable, approach to fuel-efficient interplanetary travel.
Go by tube.
It’s an idea straight out of science fiction. In his 2004 Pandora’s Star, Peter Hamilton portrays a future where people travel to planets encircling distant stars by train, running the railway lines through a wormhole, a short cut through space-time. In his Lensman series from 1934 to 1948, Edward Elmer ‘Doc’ Smith came up with the hyperspatial tube, which malevolent aliens used to invade human worlds from the fourth dimension.
Although we don’t yet have wormholes or aliens from the fourth dimension, it has been discovered that the planets and moons of the Solar System are tied together by a network of tubes, whose mathematical definition requires many more dimensions than four. The tubes provide energy-efficient routes from one world to another. They can be seen only through mathematical eyes, because they are not made of matter: their walls are energy levels. If we could visualise the ever-changing landscape of gravitational fields that controls how the planets move, we would be able to see the tubes, swirling along with the planets as they orbit the Sun.
Tubes explain some puzzling orbital dynamics. Consider, for example, the comet called Oterma. A century ago, Oterma’s orbit was well outside that of Jupiter. But after a close encounter with the giant planet, the comet’s orbit shifted inside that of Jupiter. After another close encounter, it switched back outside again. We can confidently predict that Oterma will continue to switch orbits in this way every few decades: not because it breaks Newton’s law, but because it obeys it.
This is a far cry from tidy ellipses. The orbits predicted by Newtonian gravity are elliptical only when no other bodies exert a significant gravitational pull. But the Solar System is full of other bodies, and they can make a huge – and surprising – difference. It is here that the tubes enter the story. Oterma’s orbit lies inside two tubes, which meet near Jupiter. One tube lies inside Jupiter’s orbit, the other outside. They enclose special orbits in 3 : 2 and 2 : 3 resonance with Jupiter, meaning that a body in such an orbit will go round the Sun three times for every two revolutions of Jupiter, or two times for every three. At the tube junction near Jupiter, the comet can switch tubes, or not, depending on rather subtle effects of Jovian and solar gravity. But once inside a tube, Oterma is stuck there until the tube returns to the junction. Like a train that has to stay on the rails, but can change its route to another set of rails if someone switches the points, Oterma has some freedom to change its itinerary, but not a lot (Figure 15).
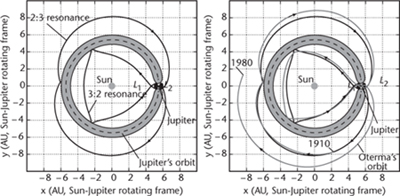
Fig 15 Left: Two periodic orbits, in 2 : 3 and 3 : 2 resonance with Jupiter, connected via Lagrange points. right: Actual orbit of comet Oterma, 1910–1980.
The tubes and their junctions may seem bizarre, but they are natural and important features of the gravitational geography of the Solar System. Victorian railway-builders understood the need to exploit natural features of the landscape, running railways through valleys and along contour lines, and digging tunnels through hills rather than taking the train over the top. One reason was that trains tend to slip on steep gradients, but the main one was energy. Climbing a hill, against the force of gravity, costs energy, which shows up as increased fuel consumption, which costs money.
It’s much the same with interplanetary travel. Imagine a spacecraft moving through space. Where it goes next does not depend solely on where it is now: it also depends on how fast it is moving and in which direction. It takes three numbers to specify the spacecraft’s position – for example its direction from the Earth, which requires two numbers (astronomers use right ascension and declination, which are analogous to longitude and latitude on the celestial sphere, the apparent sphere formed by the night sky), and its distance from the Earth. It takes a further three numbers to specify its velocity in those three directions. So the spacecraft travels through a mathematical landscape that has six dimensions rather than two.
A natural landscape is not flat: it has hills and valleys. It takes energy to climb a hill, but a train can gain energy by rolling down into a valley. In fact, two types of energy come into play. The height above sea-level determines the train’s potential energy, which represents work done against the force of gravity. The higher you go, the more potential energy you must create. The second kind is kinetic energy, which corresponds to speed. The faster you go, the greater your kinetic energy becomes. When the train rolls downhill and accelerates, it trades potential energy for kinetic. When it climbs a hill and slows down, the trade is in the reverse direction. The total energy is constant, so the train’s trajectory is analogous to a contour line in the energy landscape. However, trains have a third source of energy: coal, diesel, or electricity. By expending fuel, a train can climb a gradient or speed up, freeing itself from its natural free-running trajectory. The total energy still cannot change, but all else is negotiable.
It is much the same with spacecraft. The combined gravitational fields of the Sun, planets, and other bodies of the Solar System provide potential energy. The speed of the spacecraft corresponds to kinetic energy. And its motive power – be it rocket fuel, ions, or light-pressure – adds a further energy source, which can be switched on or off as required. The path followed by the spacecraft is a kind of contour line in the corresponding energy landscape, and along that path the total energy remains constant. And some types of contour line are surrounded by tubes, corresponding to nearby energy levels.
Those Victorian railway engineers were also aware that the terrestrial landscape has special features – peaks, valleys, mountain passes – which have a big effect on efficient routes for railway lines, because they constitute a kind of skeleton for the overall geometry of the contours. For instance, near a peak or a valley bottom the contours form closed curves. At peaks, potential energy is locally at a maximum; in a valley, it is at a local minimum. Passes combine features of both, being at a maximum in one direction, but a minimum in another. Similarly, the energy landscape of the Solar System has special features. The most obvious are the planets and moons themselves, which sit at the bottom of gravity wells, like valleys. Equally important, but less visible, are the peaks and passes of the energy landscape. All these features organise the overall geometry, and with it, the tubes.
The energy landscape has other attractive features for the tourist, notably Lagrange points. Imagine a system consisting only of the Earth and the Moon. In 1772 Joseph-Louis Lagrange discovered that at any instant there are precisely five places where the gravitational fields of the two bodies, together with centrifugal force, cancel out exactly. Three are in line with both Earth and Moon – L1 lies between them, L2 is on the far side of the Moon, and L3 is on the far side of the Earth. The Swiss mathematician Leonhard Euler had already discovered these around 1750. But there are also L4 and L5, known as Trojan points, which lie in the same orbit as the Moon but 60 degrees ahead of it or behind it. As the Moon rotates round the Earth, the Lagrange points rotate with it. Other pairs of bodies also have Lagrange points – Earth/Sun, Jupiter/Sun, Titan/Saturn.
The old-fashioned Hohmann transfer orbit is built from pieces of circles and ellipses, which are the natural trajectories for two-body systems. The new tube-based paths are built from pieces of the natural trajectories of three-body systems, such as Sun/Earth/spacecraft. Lagrange points play a special role, just as peaks and passes did for railways: they are the junctions where tubes meet. L1 is a great place to make small course changes, because the natural dynamics of a spacecraft near L1 is chaotic, Figure 16. Chaos has a useful feature (see Chapter 16): very small changes in position or speed can create large changes to the trajectory. So it is easy to redirect the spacecraft in a fuel-efficient, though possibly slow, manner.
The first person to take this idea seriously was the German-born mathematician Edward Belbruno, an orbital analyst at the Jet Propulsion Laboratory from 1985 to 1990. He realised that chaotic dynamics in many-body systems provided an opportunity for novel low-energy transfer orbits, naming the technique fuzzy boundary theory. In 1991 he put his ideas into practice. Hiten, a Japanese probe, had been surveying the Moon, and had completed its intended mission, returning to orbit the Earth. Belbruno designed a new orbit that would take it back to the Moon despite having pretty much run out of fuel. After approaching the Moon as intended, Hiten visited its L4 and L5 points to search for cosmic dust that might have been trapped there.
A similar trick was used in 1985 to redirect the almost-dead International Sun–Earth Explorer ISEE-3 to rendezvous with comet Giacobini–Zinner, and it was used again for NASA’s Genesis mission to bring back samples of the solar wind. Mathematicians and engineers wanted to repeat the trick, and to find others of the same kind, which meant finding out what really made it work. It turned out to be tubes.
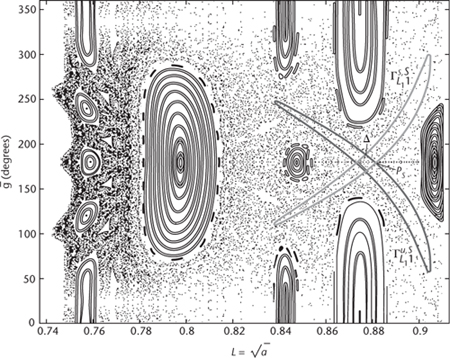
Fig 16 Chaos near Jupiter. The diagram shows a cross-section of orbits. The nested loops are quasiperiodic orbits and the remaining stippled region is a chaotic orbit. The two thin loops crossing each other at the right are cross-sections of tubes.
The underlying idea is simple but clever. Those special places in the energy landscape that resemble mountain passes create bottlenecks that would-be travellers cannot easily avoid. Ancient humans discovered, the hard way, that even though it takes energy to climb a pass, it takes more energy to follow any other route – unless you can go round the mountain in a totally different direction. The pass makes the best of a bad choice.
In the energy landscape, the analogues of passes include Lagrange points. Associated with them are very specific inbound paths, which are like the most efficient way to climb up the pass. There are also equally specific outbound paths, analogous to the natural routes down from the pass. To follow these inbound and outbound paths exactly, you have to travel at just the right speed, but if your speed is slightly different you can still stay near those paths. In the late 1960s American mathematicians Charles Conley and Richard McGehee followed up Belbruno’s pioneering work, pointing out that each such path is surrounded by a nested set of tubes, one inside the other. Each tube corresponds to a particular choice of speed; the further away it is from the optimal speed, the wider the tube is. On the surface of any given tube, the total energy is constant, but the constants differ from one tube to another. Much as a contour line is at a constant height, but that height is different for each contour.
The way to plan an efficient mission profile, then, is to work out which tubes are relevant to your choice of destination. Then you route your spacecraft along the inside of the first inbound tube, and when it gets to the associated Lagrange point you fire a quick burst on the motors to redirect it along the most suitable outbound tube, Figure 17. That tube naturally flows into the corresponding inbound tube of the next switching point. . . and so it goes.

Fig 17 Left: Tubes meeting near Jupiter. right: Close-up of region where the tubes join.
Plans for future tubular missions are already being drawn up. In 2000 Wang Sang Koon, Martin Lo, Jerrold Marsden, and Shane Ross used the tube technique to find a ‘Petit Grand Tour’ of the moons of Jupiter, ending with a capture orbit round Europa, which was very tricky with previous methods. The path involves a gravitational boost near Ganymede followed by a tube trip to Europa. A more complex route, requiring even less energy, includes Callisto as well. It makes use of another feature of the energy landscape – resonances. These occur when, say, two moons repeatedly return to the same relative positions, but one revolves twice round Jupiter while the other revolves three times. Any small numbers can replace 2 and 3 here. This route uses five-body dynamics: Jupiter, the three moons, and the spacecraft.
In 2005, Michael Dellnitz, Oliver Junge, Marcus Post, and Bianca Thiere used tubes to plan an energy-efficient mission from the Earth to Venus. The main tube here links the Sun/Earth L1 point to the Sun/Venus L2 point. As a comparison, this route uses only one third of the fuel required by the European Space Agency’s Venus Express mission, because it can use low-thrust engines; the price paid is a lengthening of the transit time from 150 days to about 650 days.
The influence of tubes may go further. In unpublished work, Dellnitz has discovered evidence of a natural system of tubes connecting Jupiter to each of the inner planets. This remarkable structure, now called the Interplanetary Superhighway, hints that Jupiter, long known to be the dominant planet of the Solar System, also plays the role of a celestial Grand Central Station. Its tubes may well have organised the formation of the entire Solar System, determining the spacings of the inner planets.
Why were the tubes not spotted sooner? Until very recently, two vital things were missing. One was powerful computers, capable of carrying out the necessary many-body calculations. They are far too cumbersome by hand. But the other, even more important, was a deep mathematical understanding of the geography of the energy landscape. Without this imaginative triumph of modern mathematical methods, there would be nothing for the computers to calculate. And without Newton’s law of gravity, the mathematical methods would never have been devised.