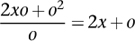
In 1665 Charles II was king of England and his capital city, London, was a sprawling metropolis of half a million people. The arts flourished, and science was in the early stages of an ever-accelerating ascendancy. The Royal Society, perhaps the oldest scientific society now in existence, had been founded five years earlier, and Charles had granted it a royal charter. The rich lived in impressive houses, and commerce was thriving, but the poor were crammed into narrow streets overshadowed by ramshackle buildings that jutted out ever further as they rose, storey by storey. Sanitation was inadequate; rats and other vermin were everywhere. By the end of 1666, one fifth of London’s population had been killed by bubonic plague, spread first by rats and then by people. It was the worst disaster in the capital’s history, and the same tragedy played out all over Europe and North Africa. The king departed in haste for the more sanitary countryside of Oxfordshire, returning early in 1666. No one knew what caused plague, and the city authorities tried everything – burning fires continually to cleanse the air, burning anything that gave off a strong smell, burying the dead quickly in pits. They killed many dogs and cats, which ironically removed two controls on the rat population.
During those two years, an obscure and unassuming undergraduate at Trinity College, Cambridge, completed his studies. Hoping to avoid the plague, he returned to the house of his birth, from which his mother managed a farm. His father had died shortly before he was born, and he had been brought up by his maternal grandmother. Perhaps inspired by rural peace and quiet, or lacking anything better to do with his time, the young man thought about science and mathematics. Later he wrote: ‘In those days I was in the prime of my life for invention, and minded mathematics and [natural] philosophy more than at any other time since.’ His researches led him to understand the importance of the inverse square law of gravity, an idea that had been hanging around ineffectually for at least 50 years. He worked out a practical method for solving problems in calculus, another concept that was in the air but had not been formulated in any generality. And he discovered that white sunlight is composed of many different colours – all the colours of the rainbow.
When the plague died down, he told no one about the discoveries he had made. He returned to Cambridge, took a master’s degree, and became a fellow at Trinity. Elected to the Lucasian Chair of Mathematics, he finally began to publish his ideas and to develop new ones.
The young man was Isaac Newton. His discoveries created a revolution in science, bringing about a world that Charles II would never have believed could exist: buildings with more than a hundred floors, horseless carriages doing 80 mph along the M6 motorway while the driver listens to music using a magic disc made from a strange glasslike material, heavier-than-air flying machines that cross the Atlantic in six hours, colour pictures that move, and boxes you carry in your pocket that talk to the other side of the world . . .
Previously, Galileo Galilei, Johannes Kepler, and others had turned up the corner of nature’s rug and seen a few of the wonders concealed beneath it. Now Newton cast the rug aside. Not only did he reveal that the universe has secret patterns, laws of nature; he also provided mathematical tools to express those laws precisely and to deduce their consequences. The system of the world was mathematical; the heart of God’s creation was a soulless clockwork universe.
The world view of humanity did not suddenly switch from religious to secular. It still has not done so completely, and probably never will. But after Newton published his Philosophiæ Naturalis Principia Mathematica (‘Mathematical Principles of Natural Philosophy’) the ‘System of the World’ – the book’s subtitle – was no longer solely the province of organised religion. Even so, Newton was not the first modern scientist; he had a mystical side too, devoting years of his life to alchemy and religious speculation. In notes for a lecture1 the economist John Maynard Keynes, also a Newtonian scholar, wrote:
Newton was not the first of the age of reason. He was the last of the magicians, the last of the Babylonians and Sumerians, the last great mind which looked out on the visible and intellectual world with the same eyes as those who began to build our intellectual inheritance rather less than 10,000 years ago. Isaac Newton, a posthumous child born with no father on Christmas Day, 1642, was the last wonderchild to whom the Magi could do sincere and appropriate homage.
Today we mostly ignore Newton’s mystic aspect, and remember him for his scientific and mathematical achievements. Paramount among them are his realisation that nature obeys mathematical laws and his invention of calculus, the main way we now express those laws and derive their consequences. The German mathematician and philosopher Gottfried Wilhelm Leibniz also developed calculus, more or less independently, at much the same time, but he did little with it. Newton used calculus to understand the universe, though he kept it under wraps in his published work, recasting it in classical geometric language. He was a transitional figure who moved humanity away from a mystical, medieval outlook and ushered in the modern rational world view. After Newton, scientists consciously recognised that the universe has deep mathematical patterns, and were equipped with powerful techniques to exploit that insight.
The calculus did not arise ‘out of the blue’. It came from questions in both pure and applied mathematics, and its antecedents can be traced back to Archimedes. Newton himself famously remarked, ‘If I have seen a little further it is by standing on the shoulders of giants.’2 Paramount among those giants were John Wallis, Pierre de Fermat, Galileo, and Kepler. Wallis developed a precursor to calculus in his 1656 Arithmetica Infinitorum (‘Arithmetic of the Infinite’). Fermat’s 1679 De Tangentibus Linearum Curvarum (‘On Tangents to Curved Lines’) presented a method for finding tangents to curves, a problem intimately related to calculus. Kepler formulated three basic laws of planetary motion, which led Newton to his law of gravity, the subject of the next chapter. Galileo made big advances in astronomy, but he also investigated mathematical aspects of nature down on the ground, publishing his discoveries in De Motu (‘On Motion’) in 1590. He investigated how a falling body moves, finding an elegant mathematical pattern. Newton developed this hint into three general laws of motion.
To understand Galileo’s pattern we need two everyday concepts from mechanics: velocity and acceleration. Velocity is how fast something is moving, and in which direction. If we ignore the direction, we get the body’s speed. Acceleration is a change in velocity, which usually involves a change in speed (an exception arises when the speed remains the same but the direction changes). In everyday life we use acceleration to mean speeding up and deceleration for slowing down, but in mechanics both changes are accelerations: the first positive, the second negative. When we drive along a road the speed of the car is displayed on the speedometer – it might, for instance, be 50 mph. The direction is whichever way the car is pointing. When we put our foot down, the car accelerates and the speed increases; when we stamp on the brakes, the car decelerates – negative acceleration.
If the car is moving at a fixed speed, it’s easy to work out what that speed is. The abbreviation mph gives it away: miles per hour. If the car travels 50 miles in 1 hour, we divide the distance by the time, and that’s the speed. We don’t need to drive for an hour: if the car goes 5 miles in 6 minutes, both distance and time are divided by 10, and their ratio is still 50 mph. In short,
speed = distance travelled divided by time taken.
In the same way, a fixed rate of acceleration is given by
acceleration = change in speed divided by time taken.
This all seems straightforward, but conceptual difficulties arise when the speed or acceleration is not fixed. And they can’t both be constant, because constant (and nonzero) acceleration implies a changing speed. Suppose you drive along a country lane, speeding up on the straights, slowing for the corners. Your speed keeps changing, and so does your acceleration. How can we work them out at any given instant of time? The pragmatic answer is to take a short interval of time, say a second. Then your instantaneous speed at (say) 11.30 am is the distance you travel between that moment and one second later, divided by one second. The same goes for instantaneous acceleration.
Except . . . that’s not quite your instantaneous speed. It’s really an average speed, over a one-second interval of time. There are circumstances in which one second is a huge length of time – a guitar string playing middle C vibrates 440 times every second; average its motion over an entire second and you’ll think it’s standing still. The answer is to consider a shorter interval of time – one ten thousandth of a second, perhaps. But this still doesn’t capture instantaneous speed. Visible light vibrates one quadrillion (1015) times every second, so the appropriate time interval is less than one quadrillionth of a second. And even then . . . well, to be pedantic, that’s still not an instant. Pursuing this line of thought, it seems to be necessary to use an interval of time that is shorter than any other interval. But the only number like that is 0, and that’s useless, because now the distance travelled is also 0, and 0/0 is meaningless.
Early pioneers ignored these issues and took a pragmatic view. Once the probable error in your measurements exceeds the increased precision you would theoretically get by using smaller intervals of time, there’s no point in doing so. The clocks in Galileo’s day were very inaccurate, so he measured time by humming tunes to himself – a trained musician can subdivide a note into very short intervals. Even then, timing a falling body is tricky, so Galileo hit on the trick of slowing the motion down by rolling balls down an inclined slope. Then he observed the position of the ball at successive intervals of time. What he found (I’m simplifying the numbers to make the pattern clear, but it’s the same pattern) is that for times 0, 1, 2, 3, 4, 5, 6, . . . these positions were
0 1 4 9 16 25 36
The distance was (proportional to) the square of the time. What about the speeds? Averaged over successive intervals, these were the differences
1 3 5 7 9 11
between the successive squares. In each interval, other than the first, the average speed increased by 2 units. It’s a striking pattern – all the more so to Galileo when he dug something very similar out of dozens of measurements with balls of many different masses on slopes with many different inclinations.
From these experiments and the observed pattern, Galileo deduced something wonderful. The path of a falling body, or one thrown into the air, such as a cannonball, is a parabola. This is a U-shaped curve, known to the ancient Greeks. (The U is upside down in this case. I’m ignoring air resistance, which changes the shape: it didn’t have much effect on Galileo’s rolling balls.) Kepler encountered a related curve, the ellipse, in his analysis of planetary orbits: this must have seemed significant to Newton too, but that story must wait until the next chapter.
With only this particular series of experiments to go on, it’s not clear what general principles underlie Galileo’s pattern. Newton realised that the source of the pattern is rates of change. Velocity is the rate at which position changes with respect to time; acceleration is the rate at which velocity changes with respect to time. In Galileo’s observations, position varied according to the square of time, velocity varied linearly, and acceleration didn’t vary at all. Newton realised that in order to gain a deeper understanding of Galileo’s patterns, and what they meant for our view of nature, he had to come to grips with instantaneous rates of change. When he did, out popped calculus.
You might expect an idea as important as calculus to be announced with a fanfare of trumpets and parades through the streets. However, it takes time for the significance of novel ideas to sink in and to be appreciated, and so it was with calculus. Newton’s work on the topic dates from 1671 or earlier, when he wrote The Method of Fluxions and Infinite Series. We are unsure of the date because the book was not published until 1736, nearly a decade after his death. Several other manuscripts by Newton also refer to ideas that we now recognise as differential and integral calculus, the two main branches of the subject. Leibniz’s notebooks show that he obtained his first significant results in calculus in 1675, but he published nothing on the topic until 1684.
After Newton had risen to scientific prominence, long after both men had worked out the basics of calculus, some of Newton’s friends sparked a largely pointless but heated controversy about priority, accusing Leibniz of plagiarising Newton’s unpublished manuscripts. A few mathematicians from continental Europe responded with counter-claims of plagiarism by Newton. English and continental mathematicians were scarcely on speaking terms for a century, which caused huge damage to English mathematicians, but none whatsoever to the continental ones. They developed calculus into a central tool of mathematical physics while their English counterparts were seething about insults to Newton instead of exploiting insights from Newton. The story is tangled and still subject to scholarly disputation by historians of science, but broadly speaking it seems that Newton and Leibniz discovered the basic ideas of calculus independently – at least, as independently as their common mathematical and scientific culture permitted.
Leibniz’s notation differs from Newton’s, but the underlying ideas are more or less identical. The intuition behind them, however, is different. Leibniz’s approach was a formal one, manipulating algebraic symbols. Newton had a physical model at the back of his mind, in which the function under consideration was a physical quantity that varies with time. This is where his curious term ‘fluxion’ comes from – something that flows as time passes.
Newton’s method can be illustrated using an example: a quantity y that is the square x2 of another quantity x. (This is the pattern that Galileo found for a rolling ball: its position is proportional to the square of the time that has elapsed. So there y would be position and x time. The usual symbol for time is t, but the standard coordinate system in the plane uses x and y.) Start by introducing a new quantity o, denoting a small change in x. The corresponding change in y is the difference
(x + o)2 − x2
which simplifies to 2xo + o2. The rate of change (averaged over a small interval of length o, as x increases to x + o) is therefore
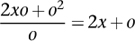
This depends on o, which is only to be expected since we are averaging the rate of change over a nonzero interval. However, if o becomes smaller and smaller, ‘flowing towards’ zero, the rate of change 2x + o gets closer and closer to 2x. This does not depend on o, and it gives the instantaneous rate of change at x.
Leibniz performed essentially the same calculation, replacing o by dx (‘small difference in x’), and defining dy to be the corresponding small change in y. When a variable y depends on another variable x, the rate of change of y with respect to x is called the derivative of y. Newton wrote the dy derivative of y by placing a dot above it: 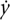 . Leibniz wrote
. Leibniz wrote 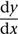 . For higher derivatives, Newton used more dots, while Leibniz wrote things like
. For higher derivatives, Newton used more dots, while Leibniz wrote things like 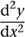 . Today we say that y is a function of x and write y = f(x), but this concept existed only in rudimentary form at the time. We either use Leibniz’s notation, or a variant of Newton’s in which the dot is replaced by a dash, which is easier to print: y’, y”. We also write f’(x) and f”(x) to emphasise that the derivatives are themselves functions. Calculating the derivative is called differentiation.
. Today we say that y is a function of x and write y = f(x), but this concept existed only in rudimentary form at the time. We either use Leibniz’s notation, or a variant of Newton’s in which the dot is replaced by a dash, which is easier to print: y’, y”. We also write f’(x) and f”(x) to emphasise that the derivatives are themselves functions. Calculating the derivative is called differentiation.
Integral calculus – finding areas – turns out to be the inverse of differential calculus – finding slopes. To see why, imagine adding a thin slice on the end of the shaded area of Figure 12. This slice is very close to a long thin rectangle, of width o and height y. Its area is therefore very close to oy. The rate at which the area changes, with respect to x, is the ratio oy/o, which equals y. So the derivative of the area is the original function. Both Newton and Leibniz understood that the way to calculate the area, a process called integration, is the reverse of differentiation in this sense. Leibniz first wrote the integral using the symbol omn., short for omnia, or ‘sum’, in Latin. Later he changed this to ∫, an old-fashioned long s, also standing for ‘sum’. Newton had no systematic notation for the integral.
Fig 12 Adding a thin slice to the area beneath the curve y = f(x).
Newton did make one crucial advance, however. Wallis had calculated the derivative of any power xa: it is axa−1. So the derivatives of x3, x4, x5 are 3x2, 4x3, 5x4, for example. He had extended this result to any polynomial – a finite combination of powers, such as 3x7 − 25x4 + x2 − 3. The trick is to consider each power separately, find the corresponding derivatives, and combine them in the same manner. Newton noticed that the same method worked for infinite series, expressions involving infinitely many powers of the variable. This let him perform the operations of calculus on many other expressions, more complicated than polynomials.
Given the close correspondence between the two versions of calculus, differing mainly in unimportant features of the notation, it is easy to see how a priority dispute might have arisen. However, the basic idea is a fairly direct formulation of the underlying question, so it is also easy to see how Newton and Leibniz could have arrived at their versions independently, despite the similarities. In any case, Fermat and Wallis had beaten them both to many of their results. The dispute was pointless.
A more fruitful controversy concerned the logical structure of calculus, or more precisely, the illogical structure of calculus. A leading critic was the Anglo-Irish philosopher George Berkeley, Bishop of Cloyne. Berkeley had a religious agenda; he felt that the materialist view of the world that was developing from Newton’s work represented God as a detached creator who stood back from his creation as soon as it got going and thereafter left it to its own devices, quite unlike the personal, immanent God of Christian belief. So he attacked logical inconsistencies in the foundations of calculus, presumably hoping to discredit the resulting science. His attack had no discernible effect on the progress of mathematical physics, for a straightforward reason: the results obtained using calculus shed so much insight into nature, and agreed so well with experiment, that the logical foundations seemed unimportant. Even today, physicists still take this view: if it works, who cares about logical hair-splitting?
Berkeley argued that it makes no logical sense to maintain that a small quantity (Newton’s o, Leibniz’s dx) is nonzero for most of a calculation, and then to set it to zero, if you have previously divided both the numerator and the denominator of a fraction by that very quantity. Division by zero is not an acceptable operation in arithmetic, because it has no unambiguous meaning. For example, 0 × 1 = 0 × 2, since both are 0, but if we divide both sides of this equation by 0 we get 1 = 2, which is false.3 Berkeley published his criticisms in 1734 in a pamphlet The Analyst, a Discourse Addressed to an Infidel Mathematician.
Newton had, in fact, attempted to sort out the logic, by appealing to a physical analogy. He saw o not as a fixed quantity, but as something that flowed – varied with time – getting closer and closer to zero without ever actually getting there. The derivative was also defined by a quantity that flowed: the ratio of the change in y to that of x. This ratio also flowed towards something, but never got there; that something was the instantaneous rate of change – the derivative of y with respect to x. Berkeley dismissed this idea as the ‘ghost of a departed quantity’.
Leibniz too had a persistent critic, the geometer Bernard Nieuwentijt, who put his criticisms into print in 1694 and 1695. Leibniz had not helped his case by trying to justify his method in terms of ‘infinitesimals’, a term open to misinterpretation. However, he did explain that what he meant by this term was not a fixed nonzero quantity that can be arbitrarily small (which makes no logical sense) but a variable nonzero quantity that can become arbitrarily small. Newton’s and Leibniz’s defences were essentially identical. To their opponents, both must have sounded like verbal trickery.
Fortunately, the physicists and mathematicians of the day did not wait for the logical foundations of calculus to be sorted out before they applied it to the frontiers of science. They had an alternative way to make sure they were doing something sensible: comparison with observations and experiments. Newton himself invented calculus for precisely this purpose. He derived laws for how bodies move when a force is applied to them, and combined these with a law for the force exerted by gravity to explain many riddles about the planets and other bodies of the Solar System. His law of gravity is such a pivotal equation in physics and astronomy that it deserves, and gets, a chapter of its own (the next one). His law of motion – strictly, a system of three laws, one of which contained most of the mathematical content – led fairly directly to calculus.
Ironically, when Newton published these laws and their scientific applications in his Principia, he eliminated all traces of calculus and replaced it by classical geometric arguments. He probably thought that geometry would be more acceptable to his intended audience, and if he did, he was almost certainly right. However, many of his geometric proofs are either motivated by calculus, or depend on the use of calculus techniques to determine the correct answers, upon which the strategy of the geometric proof relies. This is especially clear, to modern eyes, in his treatment of what he called ‘generated quantities’ in Book II of Principia. These are quantities that increase or decrease by ‘continual motion or flux’, the fluxions of his unpublished book. Today we would call them continuous (indeed differentiable) functions. In place of explicit operations of the calculus, Newton substituted a geometric method of ‘prime and ultimate ratios’. His opening lemma (the name given to an auxiliary mathematical result that is used repeatedly but has no intrinsic interest in its own right) gives the game away, because it defines equality of these flowing quantities like this:
Quantities, and the ratios of quantities, which in any finite time converge continually to equality, and before the end of that time approach nearer to each other than by any given difference, become ultimately equal.
In Never at Rest, Newton’s biographer Richard Westfall explains how radical and novel this lemma was: ‘Whatever the language, the concept . . . was thoroughly modern; classical geometry had contained nothing like it.’4 Newton’s contemporaries must have struggled to figure out what Newton was getting at. Berkeley presumably never did, because – as we will shortly see – it contains the basic idea needed to dispose of his objection.
Calculus, then, was playing an influential role behind the scenes of the Principia, but it made no appearance on stage. As soon as calculus peeped out from behind the curtains, however, Newton’s intellectual successors quickly reverse-engineered his thought processes. They rephrased his main ideas in the language of calculus, because this provided a more natural and more powerful framework, and set out to conquer the scientific world.
The clue was already visible in Newton’s laws of motion. The question that led Newton to these laws was a philosophical one: what causes a body to move, or to change its state of motion? The classical answer was Aristotle’s: a body moves because a force is applied to it, and this affects its velocity. Aristotle also stated that in order to keep a body moving, the force must continue to be applied. You can test Aristotle’s statements by placing a book or similar object on a table. If you push the book, it starts to move, and if you keep pushing with much the same force it continues to slide over the table at a roughly constant velocity. If you stop pushing, the book stops moving. So Aristotle’s views seem to agree with experiment. However, the agreement is superficial, because the push is not the only force that acts on the book. There is also friction with the surface of the table. Moreover, the faster the book moves, the greater the friction becomes – at least, while the book’s velocity remains reasonably small. When the book is moving steadily across the table, propelled by a steady force, the frictional resistance cancels out the applied force, and the total force acting on the body is actually zero.
Newton, following earlier ideas of Galileo and Descartes, realised this. The resulting theory of motion is very different from Aristotle’s. Newton’s three laws are:
First law. Every body continues in its state of rest, or of uniform motion in a right [straight] line, unless it is compelled to change that state by forces impressed upon it.
Second law. The change of motion is proportional to the motive power impressed, and is made in the direction of the right line in which that force is impressed. (The constant of proportionality is the reciprocal of the body’s mass; that is, 1 divided by that mass.)
Third law. To every action there is always opposed an equal reaction.
The first law explicitly contradicts Aristotle. The third law says that if you push something, it pushes back. The second law is where calculus comes in. By ‘change of motion’ Newton meant the rate at which the body’s velocity changes: its acceleration. This is the derivative of velocity with respect to time, and the second derivative of position. So Newton’s second law of motion specifies the relation between a body’s position, and the forces that act on it, in the form of a differential equation:
second derivative of position = force/mass
To find the position itself, we have to solve this equation, deducing the position from its second derivative.
This line of thought leads to a simple explanation of Galileo’s observations of a rolling ball. The crucial point is that the acceleration of the ball is constant. I stated this previously, using a rough-and-ready calculation applied at discrete intervals of time; now we can do it properly, allowing time to vary continuously. The constant is related to the force of gravity and the angle of the slope, but here we don’t need that much detail. Suppose that the constant acceleration is a. Integrating the corresponding function, the velocity down the slope at time t is at + b, where b is the velocity at time zero. Integrating again, the position down the slope is 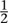 at2 + bt + c, where c is the position at time zero. In the special case a = 2, b = 0, c = 0 the successive positions fit my simplified example: the position at time t is t2. A similar analysis recovers Galileo’s major result: the path of a projectile is a parabola.
at2 + bt + c, where c is the position at time zero. In the special case a = 2, b = 0, c = 0 the successive positions fit my simplified example: the position at time t is t2. A similar analysis recovers Galileo’s major result: the path of a projectile is a parabola.
Newton’s laws of motion did not just provide a way to calculate how bodies move. They led to deep and general physical principles. Paramount among these are ‘conservation laws’, telling us that when a system of bodies, no matter how complicated, moves, certain features of that system do not change. Amid the tumult of the motion, a few things remain serenely unaffected. Three of these conserved quantities are energy, momentum, and angular momentum.
Energy can be defined as the capacity to do work. When a body is raised to a certain height, against the (constant) force of gravity, the work done to put it there is proportional to the body’s mass, the force of gravity, and the height to which it is raised. Conversely, if we then let the body go, it can perform the same amount of work when it falls back to its original height. This type of energy is called potential energy.
On its own, potential energy would not be terribly interesting, but there is a beautiful mathematical consequence of Newton’s second law of motion leading to a second kind of energy: kinetic energy. As a body moves, both its potential energy and its kinetic energy change. But the change in one exactly compensates for the change in the other. As the body descends under gravity, it speeds up. Newton’s law allows us to calculate how its velocity changes with height. It turns out that the decrease in potential energy is exactly equal to half the mass times the square of the velocity. If we give that quantity a name – kinetic energy – then the total energy, potential plus kinetic, is conserved. This mathematical consequence of Newton’s laws proves that perpetual motion machines are impossible: no mechanical device can keep going indefinitely and do work without some external input of energy.
Physically, potential and kinetic energy seem to be two different things; mathematically, we can trade one for the other. It is as if motion somehow converts potential energy into kinetic. ‘Energy’, as a term applicable to both, is a convenient abstraction, carefully defined so that it is conserved. As an analogy, travellers can convert pounds into dollars. Currency exchanges have tables of exchange rates, asserting that, say, 1 pound is of equal value to 1.4693 dollars. They also deduct a sum of money for themselves. Subject to technicalities of bank charges and so on, the total monetary value involved in the transaction is supposed to balance out: the traveller gets exactly the amount in dollars that corresponds to their original sum in pounds, minus various deductions. However, there isn’t a physical thing built into banknotes that somehow gets swapped out of a pound note into a dollar note and some coins. What gets swapped is the human convention that these particular items have monetary value.
Energy is a new kind of ‘physical’ quantity. From a Newtonian viewpoint, quantities such as position, time, velocity, acceleration, and mass have direct physical interpretations. You can measure position with a ruler, time with a clock, velocity and acceleration using both pieces of apparatus, and mass with a balance. But you don’t measure energy using an energy meter. Agreed, you can measure certain specific types of energy. Potential energy is proportional to height, so a ruler will suffice if you know the force of gravity. Kinetic energy is half the mass times the square of the velocity: use a balance and a speedometer. But energy, as a concept, is not so much a physical thing as a convenient fiction that helps to balance the mechanical books.
Momentum, the second conserved quantity, is a simple concept: mass times velocity. It comes into play when there are several bodies. An important example is a rocket; here one body is the rocket and the other is its fuel. As fuel is expelled by the engine, conservation of momentum implies that the rocket must move in the opposite direction. This is how a rocket works in a vacuum.
Angular momentum is similar, but it relates to spin rather than velocity. It is also central to rocketry, indeed the whole of mechanics, terrestrial or celestial. One of the biggest puzzles about the Moon is its large angular momentum. The current theory is that the Moon was splashed off when a Mars-sized planet hit the Earth about 4.5 billion years ago. This explains the angular momentum, and until recently was generally accepted, but it now seems that the Moon has too much water in its rocks. Such an impact should have boiled a lot of the water away.5 Whatever the eventual outcome, angular momentum is of central importance here.
Calculus works. It solves problems in physics and geometry, getting the right answers. It even leads to new and fundamental physical concepts like energy and momentum. But that doesn’t answer Bishop Berkeley’s objection. Calculus has to work as mathematics, not just agree with physics. Both Newton and Leibniz understood that o or dx cannot be both zero and nonzero. Newton tired to escape from the logical trap by employing the physical image of a fluxion. Leibniz talked of infinitesimals. Both referred to quantities that approach zero without ever getting there – but what are these things? Ironically, Berkeley’s gibe about ‘ghosts of departed quantities’ comes close to resolving the issue, but what he failed to take account of – and what both Newton and Leibniz emphasised – was how the quantities departed. Make them depart in the right way and you can leave a perfectly well-formed ghost. If either Newton or Leibniz had framed their intuition in rigorous mathematical language, Berkeley might have understood what they were getting at.
The central question is one that Newton failed to answer explicitly because it seemed obvious. Recall that in the example where y = x2, Newton obtained the derivative as 2x + o, and then asserted that as o flows towards zero, 2x + o flows towards 2x. This may seem obvious, but we can’t set o = 0 to prove it. It is true that we get the right result by doing that, but this is a red herring.6 In Principia Newton slid round this issue altogether, replacing 2x + o by his ‘prime ratio’ and 2x by his ‘ultimate ratio’. But the real key to progress is to tackle the issue head on. How do we know that the closer o approaches zero, the closer 2x + o approaches 2x? It may seem a rather pedantic point, but if I’d used more complicated examples the correct answer might not seem so plausible.
When mathematicians returned to the logic of calculus, they realised that this apparently simple question was the heart of the matter. When we say that o approaches zero, we mean that given any nonzero positive number, o can be chosen to be smaller than that number. (This is obvious: let o be half that number, for instance.) Similarly, when we say that 2x + o approaches 2x, we mean that the difference approaches zero, in the previous sense. Since the difference happens to be o itself in this case, that’s even more obvious: whatever ‘approaches zero’ means, clearly o approaches zero when o approaches zero. A more complicated function than the square would require a more complicated analysis.
The answer to this key question is to state the process in formal mathematical terms, avoiding ideas of ‘flow’ altogether. This breakthrough came about through the work of the Bohemian mathematician and theologian Bernard Bolzano and the German mathematician Karl Weierstrass. Bolzano’s work dates from 1816, but it was not appreciated until about 1870 when Weierstrass extended the formulation to complex functions. Their answer to Berkeley was the concept of a limit. I’ll state the definition in words and leave the symbolic version to the Notes.7 Say that a function f(h) of a variable h tends to a limit L as h tends to zero if, given any positive nonzero number, the difference between f(h) and L can be made smaller than that number by choosing sufficiently small nonzero values of h. In symbols,
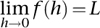
The idea at the heart of calculus is to approximate the rate of change of a function over a small interval h, and then take the limit as h tends to zero. For a general function y = f(x) this procedure leads to the equation that decorates the opening of this chapter, but using a general variable x instead of time:
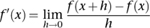
In the numerator we see the change in f; the denominator is the change in x. This equation defines the derivative f′(x) uniquely, provided the limit exists. That has to be proved for any function under consideration: the limit does exist for most of the standard functions – squares, cubes, higher powers, logarithms, exponentials, trigonometric functions.
Nowhere in the calculation do we ever divide by zero, because we never set h = 0. Moreover, nothing here actually flows. What matters is the range of values that h can assume, not how it moves through that range. So Berkeley’s sarcastic characterisation is actually spot on. The limit L is the ghost of the departed quantity – my h, Newton’s o. But the manner of the quantity’s departure – approaching zero, not reaching it – leads to a perfectly sensible and logically well-defined ghost.
Calculus now had a sound logical basis. It deserved, and acquired, a new name to reflect its new status: analysis.
It is no more possible to list all the ways that calculus can be applied than it is to list everything in the world that depends on using a screwdriver. On a simple computational level, applications of calculus include finding lengths of curves, areas of surfaces and complicated shapes, volumes of solids, maximum and minimum values, and centres of mass. In conjunction with the laws of mechanics, calculus tells us how to work out the trajectory of a space rocket, the stresses in rock at a subduction zone that might produce an earthquake, the way a building will vibrate if an earthquake hits, the way a car bounces up and down on its suspension, the time it takes a bacterial infection to spread, the way a surgical wound heals, and the forces that act on a suspension bridge in a high wind.
Many of these applications stem from the deep structure of Newton’s laws: they are models of nature stated as differential equations. These are equations involving derivatives of an unknown function, and techniques from calculus are needed to solve them. I will say no more here, because every chapter from Chapter 8 onwards involves calculus explicitly, mainly in the guise of differential equations. The sole exception is Chapter 15 on information theory, and even there other developments that I don’t mention also involve calculus. Like the screwdriver, calculus is simply an indispensable tool in the engineer’s and scientist’s toolkits. More than any other mathematical technique, it has created the modern world.