The Princeton Guide to Evolution

II.3

Molecular Clock Dating

Bruce Rannala and Ziheng Yang

OUTLINE

1. The molecular evolutionary clock

2. Molecular clock dating

3. Testing the molecular clock

4. Statistical methods for divergence time estimation

5. Maximum likelihood estimation of divergence times

6. Bayesian estimation of divergence times

7. Fossil calibrations

8. Relaxed clocks and prior model of rate drift

9. Perspectives

This chapter reviews the history of the molecular clock, its impact on molecular evolution, and the controversies surrounding mechanisms of evolutionary rate variation and the application of the clock to date species divergences. We review current molecular clock dating methods, including maximum likelihood and Bayesian methods, with an emphasis on relaxing the clock and on incorporating uncertainties into fossil calibrations.

GLOSSARY

Fossil Calibrations. The use of the fossil record to specify the ages of nodes (divergence events) on the phylogenetic tree. In the simplest case, an interior node on the tree is assigned a fixed age, and a molecular clock is then applied in an analysis of the sequence data to estimate the absolute ages of the remaining nodes. More sophisticated calibration methods use Bayesian methodology to accommodate uncertainties in the fossil record, by specifying a distribution for a node age (instead of a fixed constant).

Fossil/Sequence Information Plot. A regression-based method for determining how much remaining uncertainty for node ages is due to uncertainties in fossil calibration times (or lack thereof) and how much to insufficient sequence data.

Molecular Clock. The hypothesis (or observation) that DNA (or amino acid) sequences accumulate changes at a constant rate through time (and among species). A “relaxed” clock model allows rates to vary across lineages in an orderly way; there may be a “local clock” with constant rates in subsets of species (in a likelihood analysis), or there may be lineage-specific rates that are either independent observations from a common distribution or correlated between ancestral and descendant species (in a Bayesian analysis).

Nonparametric Rate-Smoothing Method. One of the first methods for modeling sequence substitution rate evolution among lineages (a relaxed molecular clock). This early heuristic procedure penalizes changes in rate between ancestral and descendant branches while maximizing the probability of the data (i.e., the likelihood), this was referred to as a penalized likelihood.

1. THE MOLECULAR EVOLUTIONARY CLOCK

In the early 1960s, it was observed that the amino acid differences between aligned hemoglobin or cytochrome c sequences from different species were roughly proportional to the times of divergence between the species (according to the fossil record). These observations led Emile Zuckerkandl and Linus Pauling to propose the hypothesis of a molecular evolutionary clock in 1965. The clock was envisaged as a stochastic one, with “ticks” corresponding to nucleotide or amino acid substitutions, which occur at random time intervals. Although particular substitutions occur at random times, the rate at which substitutions occur is assumed to be constant or “clocklike” through time and across lineages. The process is analogous to the way in which the random decay of isotopes can be used to construct an atomic clock. Furthermore, much the way that different isotopes have a characteristic rate of radioactive decay, different proteins can have different evolutionary rates, meaning that their molecular clocks tick at different rates.

The molecular clock hypothesis had an immediate and profound impact on the emerging field of molecular evolution, greatly expanding the role of molecular analysis in studies of phylogeny and the timing of significant evolutionary events; nonetheless, the molecular clock hypothesis has been a focus of controversy throughout the five decades of its history. The reliability of the clock and its implications for the mechanism of molecular evolution were a focus of immediate controversy. The molecular clock hypothesis was proposed at a time when the neo-Darwinian theory of evolution was generally accepted by evolutionary biologists, according to which the evolutionary process is dominated by natural selection. A constant rate of evolution among species as different as mice and monkeys was incompatible with that theory. Species living in different habitats, with different life histories and generation times, must be under very different regimes of selection (and therefore should have different substitution rates). When the neutral theory of molecular evolution was first proposed (by Motoo Kimura in 1968 and by Jack King and Thomas Jukes in 1969), the observed clocklike behavior of molecular evolution was considered major supporting evidence.

The neutral theory emphasizes random fixation of neutral or nearly neutral mutations (see chapter V.1). Under such a model, the rate of substitution is equal to the neutral mutation rate, independent of factors such as environmental change and population size variation. If the mutation rate is similar and the function of a protein remains the same across species (so that the same proportion of mutations are neutral), a constant substitution rate is expected. Rate differences among proteins are explained by the presupposition that different proteins are under different functional constraints, with a different proportion of amino acids experiencing neutral mutations.

The neutral theory is not the only mechanism compatible with clocklike evolution; neither does the neutral theory always predict a molecular clock. For example, the efficiency of DNA repair mechanisms may vary among lineages leading to differences in the rate of neutral mutations and a violation of the clock (but not of the neutral theory). Controversies also exist concerning whether the neutral theory predicts rate constancy over generations or over calendar time, or whether the clock applies only to silent (synonymous) DNA changes, or instead to protein evolution as well.

Since the 1980s, DNA sequences have accumulated rapidly, replacing the protein sequences predominantly used in earlier studies. DNA sequences have now been used to conduct extensive tests of the clock and to estimate evolutionary rates in different groups of organisms. An interesting early observation was that primates have lower rates of DNA substitution than rodents, and that humans have lower rates than other apes and monkeys—characterized as the primate slowdown and hominoid slowdown, respectively. Two major factors that could account for such between-species rate differences are generation time (with a shorter generation time causing more germ-line cell divisions per calendar year and a higher substitution rate) and DNA repair mechanism (with less reliable repair mechanisms associated with higher mutation [and substitution] rates). Perhaps because of the generation time effect or other correlated life history variables, for example metabolic rate, substitution rates tend to be negatively related to body size, with high rates in rodents, intermediate rates in primates, and slow rates in whales. Species with small body sizes tend to have shorter generation times and higher metabolic rates. The negative correlation between substitution rate and body size has been supported in some studies but questioned in others. The disagreements do not appear to have been resolved.

2. MOLECULAR CLOCK DATING

The molecular clock hypothesis provides a simple yet powerful way of dating evolutionary events. Under the clock assumption, the expected distance between sequences increases linearly with time of divergence. When external information about the geological ages of one or more divergence events on a phylogeny is available, based on the fossil record or certain geological events, the distances between sequences or the branch lengths on the tree can be converted into absolute geological times. This is known as molecular clock dating.

The earliest application of the clock to estimate divergence times was by Zuckerkandl and Pauling in 1962, who used an approximate clock to date duplication events among α, β, γ, and δ globins of the hemoglobin family. The molecular clock has since been used widely to date species divergences. The outcomes of molecular clock analyses have often produced controversies, usually because the molecular dates are at odds with the fossil record. One controversy concerns the origin of the major animal forms. Fossil forms of metazoan phyla appear as an “explosion” around 540 million years ago in the early Cambrian, but most molecular estimates of the ages of these divergence events have been much older, sometimes twice as old. Another controversy surrounds the origins and divergences of modern mammals and birds following the demise of the dinosaurs about 65 million years ago at the Cretaceous-Tertiary boundary (the KT boundary). Molecules again generated much older dates than expected by paleontologists.

Part of the discrepancy between molecular and fossil data is due to the incompleteness of the fossil record. Fossils provide information concerning the date by which a newly diverging lineage had developed diagnostic morphological characters. There may be a lag between the time that a lineage arose and the age of the first fossil with the derived traits of the descendants. Molecular dating, in contrast, infers ages of nodes (divergence events among ancestral lineages) in a phylogenetic tree. Fossil-based dates therefore tend to be younger than those derived from molecular data. Another source of discrepancy can be inaccuracies and deficiencies in molecular time estimation. Despite sometimes acrimonious controversies, the interactions between molecules and fossils have been a driving force in this research area, since they have prompted reinterpretations of fossils, critical evaluations of molecular dating techniques, and the development of more advanced analytical methods.

Our focus in this chapter is on statistical methods for testing the clock hypothesis, and on likelihood and Bayesian methods for dating species divergence events under global and local clock models. In such analyses, fossils are used to calibrate the clock, that is, to translate sequence distances into absolute geological times and substitution rates. A special case of molecular dating applies to viral genes, which evolve so fast that DNA substitutions may be observed over a few years (rather than thousands of millennia as with eukaryotes). One can use the dates at which particular viruses were isolated to calibrate the clock and to estimate divergence times, using essentially the same techniques as discussed here. Indeed, such dated viral sequences are sometimes referred to as “fossil sequences,” although most such samples were isolated during the last 100 years and are not true fossils.

3. TESTING THE MOLECULAR CLOCK

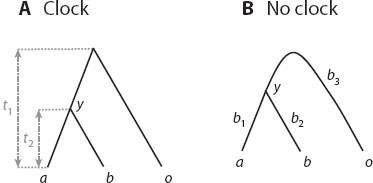
Several statistical tests have been developed to examine whether the rate of molecular evolution is constant over time. The simplest, known as the relative rate test, examines whether two species a and b evolve at the same rate by using a third out-group species o (figure 1). As species a and b share the same common ancestor y, the distance from y to a should equal the distance from y to b if the hypothesis of the molecular clock is true: d_ya = d_yb (figure 1A). Equivalently, one can formulate the clock hypothesis relative to the out-group as d_ao = d_bo and test whether the difference between the two calculated distances d = d_ao – d_bo is significantly different from 0. The sequence distances and their variances can be calculated under any model of nucleotide or amino acid substitution, and the calculated d and its standard error can be used to construct a test based on the normal distribution.

Figure 1. The relative rate test compares the rates of evolution in two species (a and b) using a third species o as the out-group.

It is also possible to conduct this relative-rate test using a likelihood ratio test. The null model assumes the clock and involves two parameters (t₁ and t₂ in figure 1A). The more general model does not assume the clock. The general model is unable to identify the root of the tree, so that the parameters in the model are the three branch lengths in the unrooted tree (b₁, b₂, b₃ in figure 1B). Note that the test is applied to sequence data alone, without knowledge of absolute times and rates, so that both the ts of figure 1A and bs of figure 1B are measured by distance, the expected number of changes per site. Using maximum likelihood analysis (see chapter II.2), one calculates the optimized log likelihood values under the null (clock) and alternative models (nonclock), ℓ₀ and ℓ₁, and then compares 2Δℓ = 2(ℓ₁ – ℓ₀) against a chi square distribution with one degree of freedom to decide whether the clock (the null model) should be rejected.

The likelihood ratio test may be applied to a tree of arbitrary size. Under the null hypothesis of the clock, there are s – 1 parameters corresponding to the ages of the s – 1 interior nodes on the rooted tree with s species. The more general nonclock model allows every branch on the unrooted tree to have its own rate, meaning there are 2s – 3 free parameters for the 2s – 3 branch lengths. Twice the log likelihood difference between the two models, 2Δℓ = 2(ℓ₁ – ℓ₀), can be compared with the χ² distribution with (2s – 3) – (s – 1) = s – 2 degrees of freedom to decide whether the clock is rejected.

Several caveats about these molecular clock tests should be noted. Although a constant rate implies the equality d_ya = d_yb in figure 1, the inverse is not necessarily true; the distances can be equal without a clock. For example, if the rate of evolution has been accelerating or decelerating over time, but the rate change affects all lineages in the same way, the tree will look clocklike, judged by the distances, even though the clock is violated. Information on absolute times of divergences is needed to detect such violations of the clock. Also, failure to reject the clock may simply be due to lack of information in the data or lack of power of the test. In general, the likelihood ratio test applied to multiple species has far more power than the relative-rate test applied to only three species.

Whether the molecular clock holds in empirical data sets depends on the level of species divergences. In general, the more ancient the divergences among the groups being studied, the less likely that a molecular clock hypothesis will be valid. For example, the molecular clock generally holds among the hominoids. Among primates, the clock may be acceptable for nuclear genes but is often rejected for faster-evolving mitochondrial genes. Among various orders of mammals, the clock is most often rejected even for nuclear data. Beyond vertebrates, the clock typically provides a very poor description of the evolutionary process.

4. STATISTICAL METHODS FOR DIVERGENCE TIME ESTIMATION

In recent years, more sophisticated statistical methods for estimating divergence times using both multiple fossil calibrations and sequence data have been developed. Both distance methods (based on calculations of pairwise distances) and likelihood methods (based on a simultaneous analysis of multiple sequences on a phylogenetic tree; see chapter II.2) can be used to estimate the distances from the internal nodes to the present time. The assumed substitution model may be important, as a simplistic model may not correct for multiple hits properly and may underestimate distances. Often the underestimation is more serious for large distances than for small ones, and the nonproportional underestimation may generate systematic biases in estimates of divergence time.

A rooted tree topology representing the ancestor-descendant relationships among lineages is typically assumed to be known in molecular clock dating, although some methods simultaneously estimate the tree and the divergence times. Uncertainties in the tree may (or may not) be important to the estimation of divergence times, for example depending on whether the uncertainties affect the placement of the fossil calibrations, and depending on the number and location of the calibration nodes. The use of several alternative, fully resolved phylogenetic tree topologies in a dating analysis may provide an assessment of the robustness of time estimation to uncertainties in the tree topology.

Besides possible errors of the substitution model and the tree topology, two additional problems that may arise are violations of the molecular clock and uncertainties in the fossil calibrations. In the past few years, considerable effort has been expended in dealing with these two problems in the likelihood and Bayesian frameworks. Below we discuss the likelihood and Bayesian methods of divergence time estimation, with an emphasis on the Bayesian method. The latter can incorporate uncertainties in fossil calibrations by specifying a prior distribution on divergence times, and it can deal with a violation of the clock through a prior model that allows substitution rate to vary across evolutionary lineages.

5. MAXIMUM LIKELIHOOD ESTIMATION OF DIVERGENCE TIMES

As mentioned above, a rooted tree of s species comprises s – 1 ancestral nodes. Suppose that the ages of c ancestral nodes are known without error, determined from fossil data. The model then involves s – c parameters: the substitution rate and the ages of the s – 1 – c nodes that are not calibration points. For example, the tree shown in figure 2 has s = 5 species, with four interior node ages: t₁, t₂, t₃, and t₄. Suppose nodes of ages t₂ and t₄ are fixed according to the fossil record. Then three parameters are estimated under the model: μ, t₁, and t₃. Given those rate and time parameters, each branch length (in units of expected substitutions) is simply the product of the rate and the time duration of the branch. For example, the length of the branch from nodes 2 to 3 in figure 2 is μ(t₂ – t₃). The likelihood function, that is to say the probability of the sequence data given the branch lengths on the tree, can be calculated using standard algorithms (see chapter II.2). Times and rates are estimated by maximizing the likelihood function.

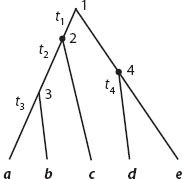
Figure 2. A tree of five species to explain the maximum likelihood and Bayesian methods for dating species divergences. Nodes 2 and 4 are the calibration nodes, while nodes 1 and 3 are the noncalibration nodes.

The description above assumes the molecular clock. What if a clock model is rejected? One possible solution is to remove some species so that the clock approximately holds for the remaining species. This may be useful if one or two lineages with grossly different rates can be identified and removed, but awkward if the rate variation is more complex. Another approach is to take explicit account of among-lineage rate variation when estimating divergence times. Considering the tree of figure 2, for example, one may assign one rate for all branches to the left of the root, and another for those to the right. This approach is known as the local-clock method. The implementation is very similar to that described for the strict molecular clock discussed above. The only difference is that, under a local-clock model with k rates of evolution, one estimates k – 1 extra rate parameters. The local-clock method may be straightforward to use if biological considerations allow us to assign branches to rate classes; however, in general, too much arbitrariness is involved in applying such a model.

Another method for accommodating among-lineage substitution rate variation in divergence date estimation, developed in the late 1990s, is Michael Sanderson’s nonparametric rate-smoothing (NPRS) method. This approach allows that the rate of substitution may evolve more slowly than the rate of lineage branching, so that closely related lineages will tend to share similar rates. One implementation of this approach, called penalized likelihood, penalizes changes in rate between ancestral and descendant branches while maximizing the probability of the data (i.e., the likelihood), thus allowing estimation of both rates and times. A smoothing parameter, λ, estimated through a cross-validation procedure, determines the importance of penalizing rate changes relative to the likelihood. Both the likelihood calculation and rate smoothing are achieved through heuristic search procedures. If a probabilistic model of rate change (see below) is instead adopted there is no need for either a rate-smoothing parameter or cross-validation. The NPRS method has the advantage that it can deal with uncertainties in the fossil calibrations, implemented by placing constraints on the ages of calibrated nodes (t_L < t < t_U); however, the NPRS method is identifiable (a necessary condition for reasonable results that depend on the data) only if at least one node age is known without error; thus the method does not provide a solution to the general problem that all fossil calibrations have some error associated with them.

6. BAYESIAN ESTIMATION OF DIVERGENCE TIMES

The Bayesian method is currently the only framework that can simultaneously incorporate multilocus sequence information, prior information on substitution rates, prior information on rates of cladogenesis, and so on, as well as fossil calibration uncertainties, to estimate divergence times. In a Bayesian analysis, one assigns prior distributions on evolutionary rates and nodal ages, and the analysis of the sequence data then generates the posterior distribution of rates and ages, on which all inference is based. Computation in Bayesian molecular dating is achieved through Markov chain Monte Carlo (MCMC) algorithms, which generate samples from the posterior distribution (see chapter II.2).

A Bayesian MCMC dating method was developed in the late 1990s by Jeff Thorne, Hiro Kishino, and Ian Painter. A model describing substitution rate change over time is used to specify the prior probability on rates, while fossil calibrations are incorporated as minimum and maximum bounds on node ages in the tree. This approach has formed the basis for several later extensions. Here we describe the general structure of these models.

Let x be the sequence data, t the s – 1 divergence times (nodal ages) and r the lineage-specific rates. Bayesian inference is based on the posterior probability of r, t, and other parameters (θ):

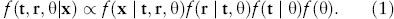
Here f(t) is the prior probability distribution on times and f(r | t, θ) is the prior on rates given the divergence times and model parameters, θ, while f(x | t, r, θ) is the likelihood function of the sequence data, x. The MCMC algorithm generates samples from the joint posterior probability distribution of times (t), rates (r) and model parameters (θ).

It should be noted that Bayesian estimation of species divergence times differs from a conventional Bayesian estimation problem, in that the errors in the posterior estimates do not approach zero when the amount of sequence data approaches infinity; indeed, theory developed by Yang and Rannala in 2006 specifies the limiting distribution of times and rates when the length of sequence approaches infinity. The theory predicts that the posterior distribution of times and rates condenses to a one-dimensional distribution as the amount of sequence data tends to infinity. Essentially there is only one free variable, and each divergence time is completely determined given the value of this variable; the variable encapsulates all the information jointly available from all the fossil calibrations. Any specific divergence time is obtained as a particular transformation of this single free variable, and the divergence time estimates are completely correlated across nodes. By examining the fossil/sequence information plot (figure 3), which is a regression of the width of the credible interval for the divergence time against the posterior mean of the divergence time, one can evaluate how closely the sequence data approach this limit. This can be used to determine whether the remaining uncertainties in the posterior time estimates are due mostly to the lack of precision in fossil calibrations or to the limited amount of sequence data. If the correlation coefficient of the regression is near 1, then little improvement in divergence dates can be gained by sequencing additional genes. This method thus allows a decision to be made as to whether digging for fossils or doing additional sequencing, or both, would be a better investment of effort. The theory highlights the critical importance of reliable and precise fossil calibrations in molecular clock dating.

Figure 3. The fossil/sequence information plot for a Bayesian analysis of primate divergence times. Two large nuclear loci are analyzed, using two fossil calibrations derived from a Bayesian analysis of primate fossil occurrence data. The rooted tree has 15 species, with 14 internal nodes. The posterior means of the ages for the 14 internal nodes are plotted against the 95% posterior credibility intervals. The correlation r = 0.9 indicates that the sequences are informative, but improvement is likely with more sequence data. The slope of the regression b = 0.49 reflects the precision of the fossil calibrations: every 100 million years of divergence adds 49 million years to the Bayesian credibility interval. (Wilkinson et al. 2011.)

7. FOSSIL CALIBRATIONS

Fossil calibrations are incorporated into a Bayesian analysis through the prior probability distribution placed on divergence times (node ages). Thorne and colleagues allowed minimum and maximum age bounds on node ages, implemented in the MCMC algorithm by not proposing new divergence times that violate such bounds. The prior for the ages of the noncalibration nodes assumes that the tree is the result of a random cladogenesis (speciation) process (a Yule pure-birth process), possibly with extinction (a birth-death process).

The bounds on node ages were “hard,” since they assign zero probability for any ages outside the interval. Such priors represent strong conviction on the part of the biologist and may not always be appropriate. In particular, fossils often provide good minimum bounds but rarely provide good maximum bounds. As a result, the researcher may be forced to use an unrealistically large maximum age bound to avoid precluding an unlikely (but not impossible) ancient age for the node. Such a “safe” approach may be problematic because the bounds may greatly influence posterior time estimation. On the other hand, failing to use a sufficiently old maximum bound can also have a pathological outcome. For example, if the true age of a fossil is larger than a hard maximum bound used in an analysis, the molecular data may conflict strongly with the fossil-based prior, resulting in overinflated confidence in the ages of other nodes.

Yang and Rannala (2006) subsequently developed more flexible distributions to mathematically describe fossil calibration uncertainties. These distributions use so-called soft bounds and assign low (but nonzero) probabilities over the whole positive half-line (t > 0). A few examples are shown in figure 4. The basic model used is a birth-death process, generalized to account for species sampling with fossil calibration information incorporated into the probability distribution by multiplying the probabilities for the branching process conditioned on the calibration ages and the probability distribution on calibration ages based on fossil information alone. A subsequent Bayesian approach to this problem by Ho and colleagues, implemented in the program Beast, did not use the “conditional” birth-death prior described above, instead multiplying unconditional probabilities, which is incorrect according to the rules of the probability calculus. The effects of this error on inferences obtained using the Beast program is difficult to judge, and the results should therefore be interpreted with caution.

Figure 4. Probability densities used to describe the likely age of a node based on the fossil record. (Redrawn according to Yang and Rannala 2006.)

Considerable effort has been spent on developing objective priors that best summarize the fossil record to represent our state of knowledge concerning the ages of calibration nodes. Studies of fossil preservation and discovery, errors in fossil dating techniques, and morphological character evolution in fossils and modern species may all contribute to this goal.

8. RELAXED CLOCKS AND PRIOR MODEL OF RATE DRIFT

Thorne and colleagues implemented a Bayesian “relaxed clock” in which substitution rates may vary across species. In their model, the rate at each node is specified by conditioning on the rate at its ancestral node. Specifically, given the rate r_A at the ancestral node, the rate r at the current node has a lognormal distribution. This means that the logarithm of the rate “drifts” according to a Brownian motion process, while the rate itself drifts according to a geometric Brownian motion process (figure 5). Parameter σ² in the Thorne et al. model controls how rapidly the rate drifts, which is to say how clocklike the tree is. A large σ² means that the rates vary rapidly over time or among branches and the clock is seriously violated, while a small σ² means that the clock roughly holds.

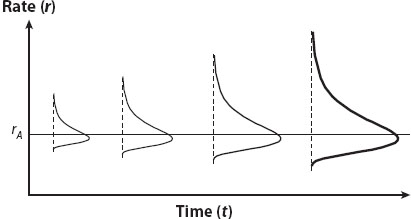
Figure 5. The geometric Brownian motion model of rate drift. Given the ancestral rate r_A time t ago, the current rate r has a lognormal distribution centered around r_A, with the variance being greater the larger t is. In other words, the logarithm of the rate y = log(r) drifts according to a Brownian motion process: given the ancestral log rate y_A = log(r_A) time t ago, the current log rate y = log(r) has a normal distribution with variance tσ². Parameter σ² measures the degree of variability of the evolutionary rate.

An alternative model of rate variation assuming independent rates was independently implemented in the late 2000s by Rannala and Yang, and by Alexei Drummond and colleagues. In this model, the rate for a branch is a random variable drawn from a common probability distribution such as the lognormal or the gamma. The rates effectively evolve independently on each lineage, but the extent of rate variation has some form of evolutionary constraint (imposed by the prior distribution on rates).

9. PERSPECTIVES

Bayesian statistics is currently the only framework that can integrate information and uncertainties from different sources in order to obtain reasonable statistical estimates of nodal ages. In particular, it can deal with violation of the molecular clock through its use of the prior model of evolutionary rate change, and it can incorporate uncertainties in the fossil calibrations by specifying prior distributions on divergence times. In contrast, attempts to achieve those two objectives in the maximum likelihood framework have been unsuccessful; nevertheless, a number of challenging problems remain in Bayesian molecular clock dating. First, use of multiple fossil calibrations in a Bayesian analysis may impose significant computational challenges. This is suggested by the observation that different dating programs may produce very different priors and thus different posterior time estimates. Second, fossil calibrations in a molecular dating analysis should be a statistical summary of the relevant part of the fossil record; thus, to generate good calibrations for a molecular dating analysis, probabilistic modeling and statistical analysis of fossil data (in particular, fossil occurrences and morphological measurements) will be necessary. Methods for molecular dating are currently the subject of intensive research and can be expected to change dramatically over the next decade. With improvements in sequence and fossil data sets, as well as more refined analytical methods, the degree of conflict between fossils and molecular data is gradually diminishing.