Game Theory and Behavior
John M. McNamara
OUTLINE
1. The basic ideas
2. Examples
3. Issues for consideration
4. Applications
5. Future directions
GLOSSARY
Best Response. A strategy that has the highest fitness given the resident strategy.
Convergence Stable. A strategy that is a local attractor under evolutionary dynamics; that is, the population strategy will evolve to this strategy if it is initially close to it.
Evolutionarily Stable Strategy (ESS). A resident strategy such that any mutant strategy (different from that of the resident) is selected against while rare and so cannot increase in frequency.
Frequency Dependence. The dependence of fitness of a given strategy on the frequency of other strategies in a population.
Mixed Strategy. A strategy in which actions are chosen probabilistically.
Monomorphic Population. A population in which only one (genetically determined) strategy is present.
Mutant Strategy. Any strategy that can arise (as a mutation); usually thought of as rare compared with the resident strategy.
Payoff Matrix. A table specifying how the increment to fitness as a result of playing a game depends on the action of the individual and that of its opponent(s).
Polymorphic Population. A population in which more than one (genetically determined) strategy is present.
Resident Strategy. A strategy that is used by almost all population members.
Symmetric Game. A game in which all players have the same set of possible actions and the same payoff matrix, and there are no role asymmetries.
1. THE BASIC IDEAS
The two main motivating ideas of evolutionary game theory are described in this section. These ideas are, however, just the basics; other necessary ingredients are discussed in section 3.
Frequency Dependence
Suppose that the environment experienced by a species is constant over many generations. Then, natural selection can be envisaged as a hill-climbing process in which species members become fitter over evolutionary time. The end point of this process is that species members will behave so as to approximately maximize fitness within this constant environment. This idea of fitness maximization is useful, since it allows us to predict and understand end points of the process of evolution without considering details of the dynamic process that led to the “top of the hill.”
However, the fitness of members of a population typically depends on the behavioral strategies of other members of the population as well as on their own behavior. For example, suppose that a foraging animal contests a food item with another population member. Then, it will be worth the animal’s being aggressive and attacking its rival if the rival is not aggressive and liable to run away if attacked; but if the rival is also liable to be aggressive, it may be better to be nonaggressive. The best strategy for the focal animal thus depends on the frequency of aggressive individuals in the population; that is, fitness, and hence the action of selection, is frequency dependent.
Even if the physical environment remains constant, when selection is frequency dependent, the “environment” experienced by members of a species changes over evolutionary time as the strategies of members of the species evolve. Thus as natural selection tends to hill climb, the shape of the hill and the position and height of its summit change. Evolutionary game theory is concerned with the outcome of evolution by natural selection in this more complex setting.
Evolutionary End Points
It is not clear that the evolutionary process will settle down to some end point when there is frequency-dependent selection; for example, strategies might cycle in their distribution of occurrence. Most of evolutionary game theory is, however, concerned with situations in which stable end points are achieved. The theory attempts to characterize the properties of possible end points.
To analyze outcomes when there is frequency dependence we use the following notation. Suppose that almost all members of a population follow a genetically determined strategy π. We then refer to π as the resident strategy. Let π′ be some possibly different strategy that is rare in occurrence compared with the resident strategy. We denote the fitness of this mutant strategy by W(π′, π). This formalism thus explicitly expresses the fitness of an individual as a function of the resident strategy as well as its own strategy.
We expect any end point to be uninvadable; that is, no mutant strategy can invade the population under the action of natural selection. To formalize this concept, suppose that the resident strategy is π*. Then, for π* to be uninvadable it is necessary that
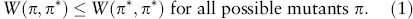
That is, when the resident strategy is π*, the fitness of residents is at least as great as that of any mutants. As we explain later, although this condition is necessary for uninvadability, it is not sufficient and needs to be strengthened.
Game theory has its roots in economics, where property (1) is the defining condition for π* to be a Nash equilibrium; the theory developed somewhat independently in biology. The concept of uninvadability is present in the early work of William D. Hamilton on stable sex ratios. Later, John Maynard Smith and George Price (1973) formalized the concept mathematically. Nowadays there is much mutual interplay between the fields of economic and evolutionary game theory.
2. EXAMPLES
The following are classic games that illustrate the basic principles of evolutionary game theory.
The Hawk-Dove Game
In their seminal paper Maynard Smith and Price modeled the behavior of two individuals that contest a resource such as a food item or mate. It is assumed that gaining the resource increases fitness by V. The model sought to explain why contests are often settled by ritualized display rather than all-out fighting. In their interaction each contestant can take one of two actions, hawk or dove. Hawks attack their opponent; doves display to their opponent and run away once attacked. The possible outcomes are as follows. When two doves interact, they share the resource. If a hawk interacts with a dove, the hawk gets the resource, since the hawk attacks and the dove runs away. If two hawks interact, they fight, and each wins the fight with probability 1/2; the winner obtains the resource, and the loser pays a fitness cost C representing the loss of fitness as a result of injuries incurred in the fight. Table 1 summarizes these fitness consequences to one (focal) individual. The opponent has exactly the same payoff matrix. We assume that the cost of injury exceeds the value of the resource (V < C).
Table 1. Payoff matrix for the Hawk-Dove game in which two population members contest a resource of value V
Payoff (fitness increment) to focal individual |
Opponent chooses hawk |
Opponent chooses dove |
Focal chooses hawk |
½V – ½C |
V |
Focal chooses dove |
0 |
½V |
For this game we may take a strategy π to specify the probability of playing hawk; that is, an individual following strategy π plays hawk with probability π and dove with probability 1 – π. Consider the payoff to a mutant that uses strategy π′ when the resident strategy is π. There are four possibilities in a contest between the mutant and a resident: (1) mutant plays hawk and resident plays hawk (a combination of actions that occurs with probability π′π), (2) mutant plays hawk and resident plays dove (occurs with probability π′(1 – π)), (3) mutant plays dove and resident plays hawk (occurs with probability (1 – π′)π), and (4) mutant plays dove and resident plays dove (occurs with probability (1 – π′)(1 – π)). Averaging over the possibilities and taking the associated payoffs into consideration (table 1), we see that the mean payoff to the mutant is
Rearranging terms, we can rewrite the preceding equation as
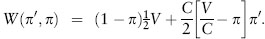
The difference between the payoff to the mutant and that to a resident is thus
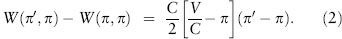
We are now in a position to find the Nash equilibrium for this game. If π < V/C, then the right-hand side of expression 2 is positive provided π′ > π. Thus any mutant that is more aggressive than the resident strategy can invade the population. If π > V/C, then expression 2 is positive provided π′ < π. Thus any mutant that is less aggressive than the resident strategy can invade. Finally, if π = V/C, then expression 2 is zero for all π. Thus when the resident strategy is to play hawk with probability π* = V/C, all possible mutants are equally fit and have the same fitness as the residents. Thus equation 1 is satisfied, and the strategy π* = V/C is a Nash equilibrium for this game. This is the only Nash equilibrium.
A Sex-Ratio Game
Suppose that female members of a population can control the sex of their offspring; should they produce sons or daughters? To consider this question in its simplest setting we consider a large population with discrete nonoverlapping generations: individuals born in one year reach maturity the next year, attempt to breed, and then die. During breeding each female mates with a single male chosen at random from the males present. The strategy of a female specifies the proportion of offspring that are sons; a female with strategy π produces a proportion π sons and a proportion 1 – π daughters. Again, for simplicity, we suppose that the number of offspring that survive to maturity does not depend on their sex.
With these assumptions, the sex of offspring does not affect the number that survive to maturity but can affect the total numbers of matings obtained by these offspring and, hence, affects the number of grandchildren produced. We take the payoff to a female to be the number of matings obtained by her offspring.
If the resident population strategy is to produce more sons than daughters (π* > 1/2), then the breeding population is male biased. Thus every male in the breeding population gets less than one mating on average. Since breeding females get exactly one mating, breeding females get more matings than males. It follows that a mutant female that produces all daughters will get a bigger payoff than resident females, so the population is invadable. If the resident strategy is to produce more daughters than sons (π* < 1/2), then each breeding male gets more than one mating on average. Thus a mutant female that produces all sons will get a higher payoff than resident females, and the population is again invadable. Finally, suppose that the resident strategy is to produce equal numbers of sons and daughters (π* = 1/2). Then, it can be seen that any mutant female that does otherwise will do exactly as well as resident females. Thus the strategy of producing equal number of sons and daughters satisfies condition 1 and is hence a Nash equilibrium.
3. ISSUES FOR CONSIDERATION
The preceding simple examples introduced some basics of evolutionary game theory, but many details and subtleties were passed over in describing them. Some of these issues are discussed next.
Strategies
Strategies are rules for choosing actions. As the Hawk-Dove game illustrates, we may allow actions to be chosen probabilistically. In the Hawk-Dove game a strategy is then simply a rule specifying the probability with which each action is chosen. In this game the Nash equilibrium is a mixed strategy in that both hawk and dove are chosen with positive probability. If instead we had constrained population members to adopt deterministic strategies, so that each either always played hawk or always played dove, then we would have predicted that the population would evolve to be polymorphic, in which a proportion 1 – (V/C) of individuals follow the strategy of always playing dove, and a proportion V/C follow the strategy of always playing hawk.
A strategy specifies the action chosen in every possible circumstance. For example, in a generalization of the Hawk-Dove game we might allow individuals to differ in fighting ability; an individual knows its own ability but not that of an opponent. A strategy for this game would specify how the probability of playing hawk depended on fighting ability. We would expect a single Nash equilibrium for this game to be of the following form: if ability exceeds a given threshold, then play hawk; otherwise play dove. Thus the existence of an underlying state (fighting ability) has changed the Nash equilibrium from a mixed strategy to one in which there are deterministic but contingent decisions. In nature most decisions are likely to be based on state rather being determined probabilistically, so the mixed-strategy Nash equilibria of much of game theory are really idealized simplifications.
Payoffs
The payoffs in a game are intended to represent the changes in fitness as a result of playing the game. Thus if a contestant receives the resource in the Hawk-Dove game, its fitness is increased by V. As this game illustrates, the payoff an individual receives can vary; for example, it can depend on the action chosen by the opponent. In an analysis of a game the mean (average) payoff is the relevant factor (see the discussion of fitness).
In considering a game-theoretical situation it is usual to specify payoffs in advance; however, this approach isolates a single play of a particular game from other parts of an individual’s life. This tactic is often artificial and can be misleading. For example, consider a game in which parents are caring for common young and each must decide whether to desert the young, leaving the partner to care for them. Suppose that the male benefits from desertion because he can attempt to find a single female and initiate another breeding attempt with her. However, his chances of finding another single female depend on how many have become available by deserting their young, and on the competition from other males that have deserted. Thus the payoff depends on the outcome of the games played by other population members. In this scenario the payoff of desertion for the male cannot be specified in advance; instead, it emerges from a holistic view of what is happening during the breeding season.
Fitness
It is usually envisaged that strategies are genetically determined and so are inherited. Natural selection acts to change the frequencies with which strategies occur. Also, the population is seen as large, with many copies of each possible genotype, so that it is possible to average; that is, the change in the frequency of strategies is determined by a suitable measure of their average reproductive success. It is this measure that is referred to as fitness. Thus, although payoffs are usually assigned to combinations of actions, in evolutionary terms what matters is the average payoff under each strategy.
In the simplest setting the fitness of a strategy is the mean number of surviving offspring produced over the lifetime of an individual that follows the strategy. In some situations, however, this measure is not adequate. For example, in the sex-ratio game outlined earlier, all females produce the same number of surviving offspring but may differ in terms of the numbers of matings obtained by these offspring and, hence, differ in terms of the numbers of their grandchildren. The mean number of surviving grandchildren is thus an appropriate fitness measure. If females differ in their phenotypic quality (for example, in dominance status), and offspring tend to inherit the quality of their mother, then even this fitness measure may not be adequate; fitness may need to be based on the mean number of great-grandchildren or beyond. The preceding fitness measures are all based on mean descendant numbers. In other situations the variance in descendant numbers may also be important.
Invasion of Mutants
The Nash equilibrium condition (inequality 1) is necessary for evolutionary stability but does not guarantee it. This condition states that if resident population members follow the Nash equilibrium strategy, then no rare mutant has higher fitness than that of the residents; but this condition does not specify what happens when a mutant has fitness equal to that of the residents. For example, the Hawk-Dove game and the sex-ratio game are both examples in which all possible rare mutants do as well as the residents at the Nash equilibrium. If rare mutants do as well as the residents, the proportion of mutants could increase by genetic drift. Furthermore, once mutants start to become common, the fitness of all population members may change, and mutants may become fitter than residents.
Motivated by these considerations Maynard Smith defined π* to be an evolutionarily stable strategy (ESS) if for every mutant strategy π ≠ π* either
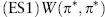
or
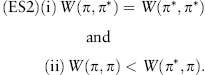
This definition of an ESS applies to a two-player game but must be modified to deal with “games against the field” such as the sex-ratio game.
For two-player games the idea behind the definition is as follows. A mutant is certainly selected against when rare if it has a strictly lower payoff against residents than residents do when playing against one another (condition ES1). Suppose, however, that a mutant does equally well when rare [condition ES2(i)]. Then, if mutant numbers start to increase by drift, they will play against one another as well as against residents. Mutants will then be selected against if they do less well than residents in interactions with other mutants [condition ES2(ii)].
In the Hawk-Dove game the Nash equilibrium strategy is to play hawk with probability V/C. This strategy is also the unique ESS for this game.
Adaptive Dynamics and Convergence Stability
The ESS condition is concerned with determining whether a population adopting a particular resident strategy π* can be invaded but says nothing about whether strategy π* will evolve in the first place. To analyze this latter question we first have to specify how the resident strategy changes as the population evolves; in other words, we have to specify the evolutionary dynamics. The exact dynamics depend on assumptions about the underlying genetic system; however, one especially simple approach known as adaptive dynamics ignores genetic detail and assumes that selection acts to locally hill climb. Given this dynamic we may consider whether a population that initially has some resident strategy π will evolve so that the resident strategy becomes π*. If this occurs for every π close to π*, then we can think of strategy π* as convergence stable.
The ESS for the Hawk-Dove game is convergence stable, but many games have at least one ESS that is not. Conversely, a strategy π* may be convergence stable but not an ESS. In such cases evolution leads toward π*, but at π* the resident strategy is at a local fitness minimum. Mutants with both smaller and greater trait values than the resident strategy can then invade, producing disruptive selection, with the possibility of evolutionary branching.
Population Fitness and Evolutionary Stability
In the Hawk-Dove game there are two contestants per contest and one resource of value V. Thus whatever strategies are used, the average value of resources obtained per individual is ½V; however, the average payoff may be lower than this owing to the cost of fighting. If all individuals play dove with probability 1, then there is no cost of fighting, and the average payoff is ½V. If instead all individuals play the ESS strategy, then there is fighting, and the average payoff is less than ½V. Thus the average payoff per individual is not maximized at the ESS.
Game theory provides many such examples in which fitness is not maximized at evolutionary stability: individuals are all doing the best for themselves, but this is not best for the population as a whole. In economic game theory an analogous idea is captured in the example of the “tragedy of the common.”
Role Asymmetries
The basic Hawk-Dove game is symmetric—there are no a priori differences in the two contestants. In contrast, consider a version of this game in which the resource contested is ownership of a territory; one individual is the current territory owner and the opponent is an intruder, with both contestants aware of their roles. Otherwise the specification of actions and payoffs are as before. For this version of the game a strategy is a rule specifying two probabilities: the probability of playing hawk when a territory owner and the probability of playing hawk when an intruder. In the original game the unique Nash equilibrium was to play hawk with probability V/C. This strategy is an ESS. In the new game there are other possibilities. For example, if all owners play hawk, then the best response in the role of intruder is to play dove. Conversely, if all intruders play dove, the best response in the role of owner is to play hawk. Thus the strategy always to play hawk when owner and always to play dove when intruder is a Nash equilibrium strategy. There are actually three Nash equilibria: (1) play hawk with probability V/C regardless of role; (2) play hawk with probability 1 when owner, and dove with probability 1 when intruder; and (3) play hawk with probability 1 when intruder, and dove with probability 1 when owner. Of these Nash equilibria the first is not an ESS; the other two are ESSs.
The preceding example illustrates a general property of games: the mere presence of asymmetry, even if it has no effect on payoffs (e.g., “owner” or “intruder”), can completely alter the predicted evolutionary outcome.
The Importance of Process
The predicted outcome of a game depends not just on the payoff structure but also on the process by which decisions are reached. For example, consider a game between parents over the care of their common young (see chapter VII.8). Each parent decides whether to care for the young. Suppose that the payoffs are as shown in table 2. These payoffs are motivated by the idea that the young do better if cared for by both parents rather than by one (and die if they receive no care), although there are costs of care. In addition, the male can get benefits from deserting (e.g., by obtaining extra-pair copulations). Note that for these payoffs the best action of the female is to care for the young whatever the action of the male.
Table 2. Payoff matrices for a game in which each of two parents decides whether to care for or to desert their common young
Payoff to the male |
Female cares |
Female deserts |
Male cares |
6 |
3 |
Male deserts |
7 |
2 |
Payoff to the female |
Male cares |
Male deserts |
Female cares |
6 |
3 |
Female deserts |
5 |
0 |
Consider first a version of the game in which both parents decided on their action without knowing the action of their partner. Suppose that the resident strategy is for the male to always desert and the female always to care. Then, no individual can do as well if it changes its action. Thus the resident strategy is a Nash equilibrium (it is also an ESS). Furthermore, it is easy to see that it is the only Nash equilibrium. Thus we predict female-only care.
In contrast, suppose that the female decides on her action first and then the male decides on his action knowing the female’s action. For this game a strategy for the female just specifies her choice of action. A strategy for the male is a contingent rule specifying what action to take if the female is caring and what action to take if she has deserted. Consider a resident population in which all females desert, and all males adopt the strategy to care if the female deserts, and desert if the female cares. In this population there is male-only care. It can be seen that this population is at a Nash equilibrium: resident males are doing the best given whatever action is taken by the female; resident females get a payoff of 5 (since males care) but would get a lower payoff of 3 if they cared (since then males would desert).
This example illustrates that the decision process is crucial to the outcome predicted. When parents are ignorant of each other’s actions, there is female-only care, and the male gets a payoff of 7. When the female chooses first, there is male-only care, and the male gets a payoff of 3. Thus knowing the action of the female lowers the male’s predicted payoff. This is an unexpected feature of behavior that game theory has uncovered—having information may put an individual at a disadvantage.
4. APPLICATIONS
Frequency dependence occurs in many aspects of an organism’s life. It is therefore not surprising that evolutionary game theory has been applied to a huge range of problems, including territorial behavior, the distribution of animals across resources, antipredator behavior, and foraging games such as those between producers and scroungers. Some further applications are described next in more detail.
Mate Choice
Suppose that males differ in some aspects of their quality, and females are choosy about their partner (see chapter VII.6). If males are no longer available to other females once chosen, there will be competition for the best males. Partner search by females will then be frequency dependent: the best strategy for a female will depend on the search and choice strategies adopted by other females.
If males are also choosy, partner choice has another game-theoretical aspect. How choosy an individual should be about his or her partner will depend on the choosiness of members of the opposite sex, as well as on his or her own quality. At a game-theoretical equilibrium the choice of strategy for males will be the best given the strategy of females, and vice versa. At this equilibrium there is liable to be assortative pairing in the population.
Parental Effort
In species with biparental care of offspring there are costs and benefits associated with parental effort. Increased care by either parent increases the prospects of the young and hence contributes to the fitness of both parents; however, an increase in level of parental care is usually costly to that parent. One obvious cost to males is the loss of opportunity to have extra-pair matings with other females. Care can also have mortality costs. For example, obtaining food for the young may incur an extra risk of predation or may require the parent to work so hard its condition suffers, and it becomes more prone to dying of disease. Since there is a joint benefit (the offspring), but costs are paid individually, there is a conflict of interest: each parent is better off if the other parent does most of the care.
The predicted level of care can be analyzed using game theory because the optimal level of care by one parent depends on the level of care provided by the other parent. Predictions depend on the assumptions made. In the simplest setting we might assume that the level of care is genetically determined, and individuals do not respond to the amount of care provided by the partner or to the state of the offspring. If instead we allow more flexible strategies, with individuals responding to circumstances, predicted levels of care are liable to be very different.
Alternative Male Mating Strategies
In some species, males in a population adopt different mating strategies (see chapter VII.4). In the Pacific salmon, males can mature as a “hook” or as a “jack.” Hooks are large individuals that defend territories and attempt to attract females to their territories to mate. Jacks are smaller, mobile individuals that attempt to sneak matings with females in the territories of hooks. The advantage of being a jack is frequency dependent; if there are many jacks, they compete with one another, and there are fewer territories. Evolutionary game theory thus provides a suitable tool for analyzing this situation.
The three examples considered all concern reproductive behavior, an area that provides the motivation for many games. Furthermore, there is often interaction among these games, so a holistic approach is required. For example, whether females should prefer a particular male may depend on the parental effort he will provide. How much effort a male should provide depends on his chances of attracting a new mate should he cease care. Thus mate choice games and parental effort games are linked.
The Evolution of Cooperation
The action of natural selection produces population members that do the best for themselves (or their genes), so it is not immediately apparent why we see cooperation between unrelated individuals in natural populations (see chapters VII.9 and VII.10). Work in this area has focused on the issue of why an individual might help another at a cost to itself, and the Prisoner’s Dilemma game has often been used to capture the underlying conundrum. In this symmetric two-player game each player can either cooperate or defect. In the simplest version of this game cooperation benefits the opponent by an amount b but costs the cooperator an amount c, where b > c. The payoff matrix is given in table 3. As can be seen, the best response of each player is to defect regardless of the action chosen by the other player. Thus the only Nash equilibrium is for both players to defect. Consequently, both receive a payoff of 0, whereas both could have received the larger payoff b – c had they both cooperated. Thus cooperation is mutually advantageous in this game but will not evolve, since a population with cooperation as the resident strategy can be invaded by an uncooperative mutant.
Table 3. The payoff matrix for a version of the Prisoner’s Dilemma game
Payoff to player 1 |
Player 2 cooperates |
Player 2 defects |
Player 1 cooperates |
b−c |
−c |
Player 1 defects |
b |
0 |
Various mechanisms that promote cooperation have been proposed. The mechanism of direct reciprocity involves population members helping those who have previously helped them (and possibly punishing those who have not given help). This mechanism has often been modeled using the Prisoner’s Dilemma game; population members pair up and play repeated rounds of this game against one another. In this interaction the action of an individual is allowed to depend on the actions chosen by itself and its opponent in previous rounds. The mechanism of indirect reciprocity involves helping those who have helped others in the past. The mechanism of generalized reciprocity involves helping another if help has been received in the past. A common feature of explanations of the evolution of cooperative behavior is that the mechanism tends to produce an assortment in which cooperators tend to interact with other cooperators.
5. FUTURE DIRECTIONS
Evolutionary game theory will continue to be applied to a range of phenomena in biology. In past applications games were largely schematic and simple, which allowed biologists to capture and understand some aspects of the world. It is increasingly being recognized, however, that important aspects that could radically alter predictions were ignored. Some of these features requiring further investigation are as follows: (1) A holistic view needs to be taken in which payoffs are not just imposed but arise as a result of embedding the game in an ecological context. (2) Game theory has largely ignored the existence of variability in natural populations and has effectively treated variability as noise. The type and amount of variability can, however, be crucial in determining the predictions of game theory. (3) Most games have assumed contestants choose a single action without knowing how the opponent(s) chose. However, the process by which individuals interact and hence reach decisions is critical to predictions. Game theory needs to pay more attention to this process. (4) Individuals are not completely flexible in their behavior; instead, they have behavioral consistencies both within and across contexts. In this sense a range of animal personalities exist within natural populations. Researchers need to better understand how much of this variation can be explained using game theory. They also need to explore the consequences of the lack of flexibility for the predictions of game theory. (5) Game theorists need to pay more attention to the decision-making mechanisms employed by animals. For example, emotions such as anger and mental states such as trust are important in human decision making, and it could be profitable to incorporate these mental states more explicitly into models.
Diekmann, O. 2004. A beginner’s guide to adaptive dynamics. Banach Center Publications 63: 47–86. Adaptive dynamics is now an important tool in game theory.
Gintis, H. 2000. Game Theory Evolving: A Problem-Centered Introduction to Modeling Strategic Interaction. Princeton, NJ: Princeton University Press. Some nice examples of simple games, from biology and other areas.
Houston, A. I., and J. M. McNamara. 1999. Models of Adaptive Behaviour: An Approach Based on State. Cambridge: Cambridge University Press. Chapter 7 provides examples of games in which players take a sequence of actions that depend on state and time.
Maynard Smith, J. 1982. Evolution and the Theory of Games. Cambridge: Cambridge University Press. A classic general introduction, although incomplete, as it does not contain more recent developments such as adaptive dynamics.
McNamara, J. M., and O. Leimar. 2010. Variation and the response to variation as a basis of successful cooperation. Philosophical Transactions of the Royal Society B 365: 2627–2633. Emphasizes how between-individual variation in population members can completely change the predictions of game theory.
McNamara, J. M., and F. J. Weissing. 2010. Evolutionary Game Theory. In T. Szekely, A. J. Moore, and J. Komdeur, eds., Social Behaviour: Genes, Ecology and Evolution. Cambridge: Cambridge University Press. A general overview that goes into more depth on some issues than this chapter does.
Oliveira, R., M. Taborsky, and H. J. Brockmann. 2008. Alternative Reproductive Tactics: An Integrative Approach. Cambridge: Cambridge University Press.
Reeve, H. K., and L. A. Dugatkin, eds. 1998. Game Theory and Animal Behavior. Oxford: Oxford University Press. Examples of the application of game theory to a variety of biological phenomena.
Sinervo, B., and R. Calsbeek. 2006. The developmental, physiological, neural, and genetical causes and consequences of frequency-dependent selection in the wild. Annual Review of Ecology and Systematics 37: 581–610.
Smith, J. M., and G. Price. 1973. The logic of animal conflict. Nature 246: 15–18. The original article that formalized game theory in biology.
van Doorn, G. S., G. M. Hengeveld, and F. J. Weissing. 2003. The evolution of social dominance. Behaviors 140: 1305–1358.