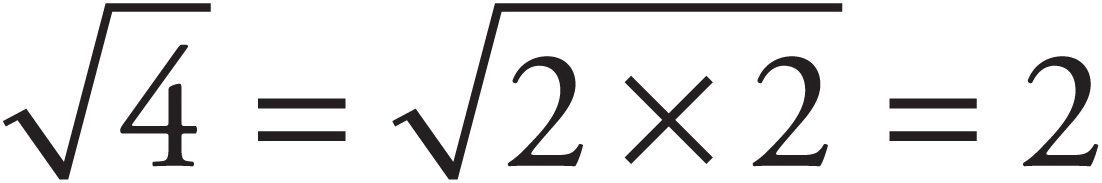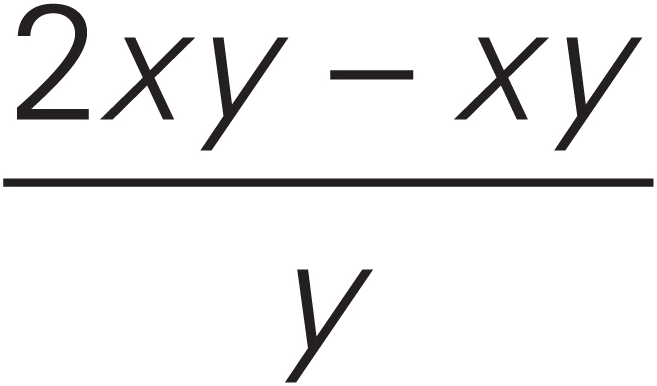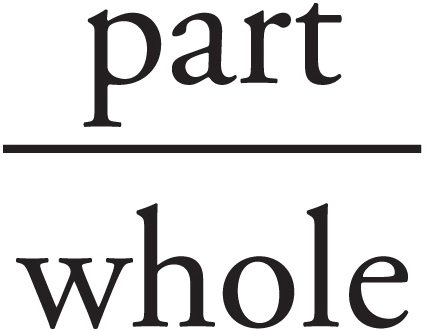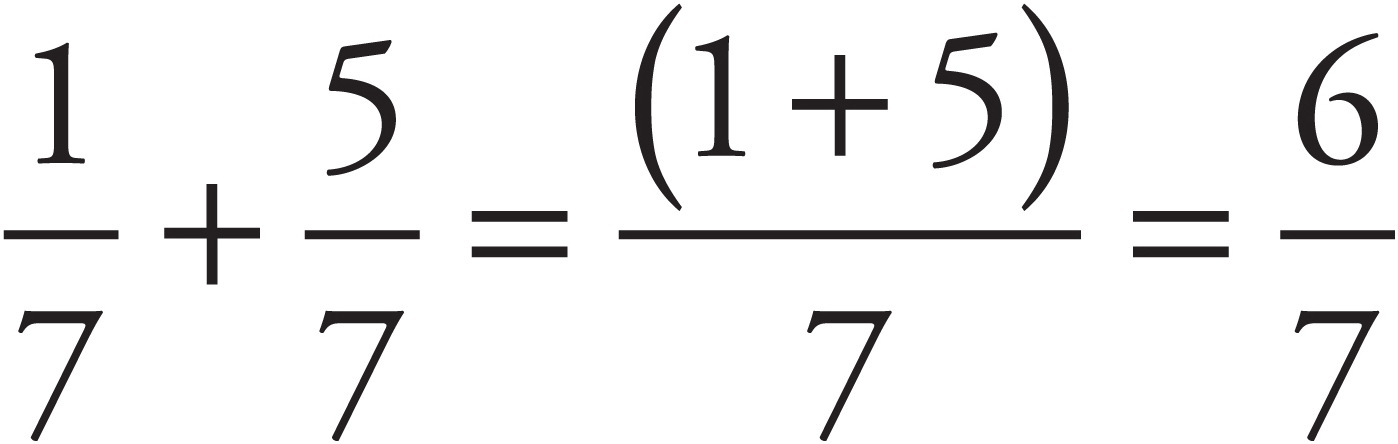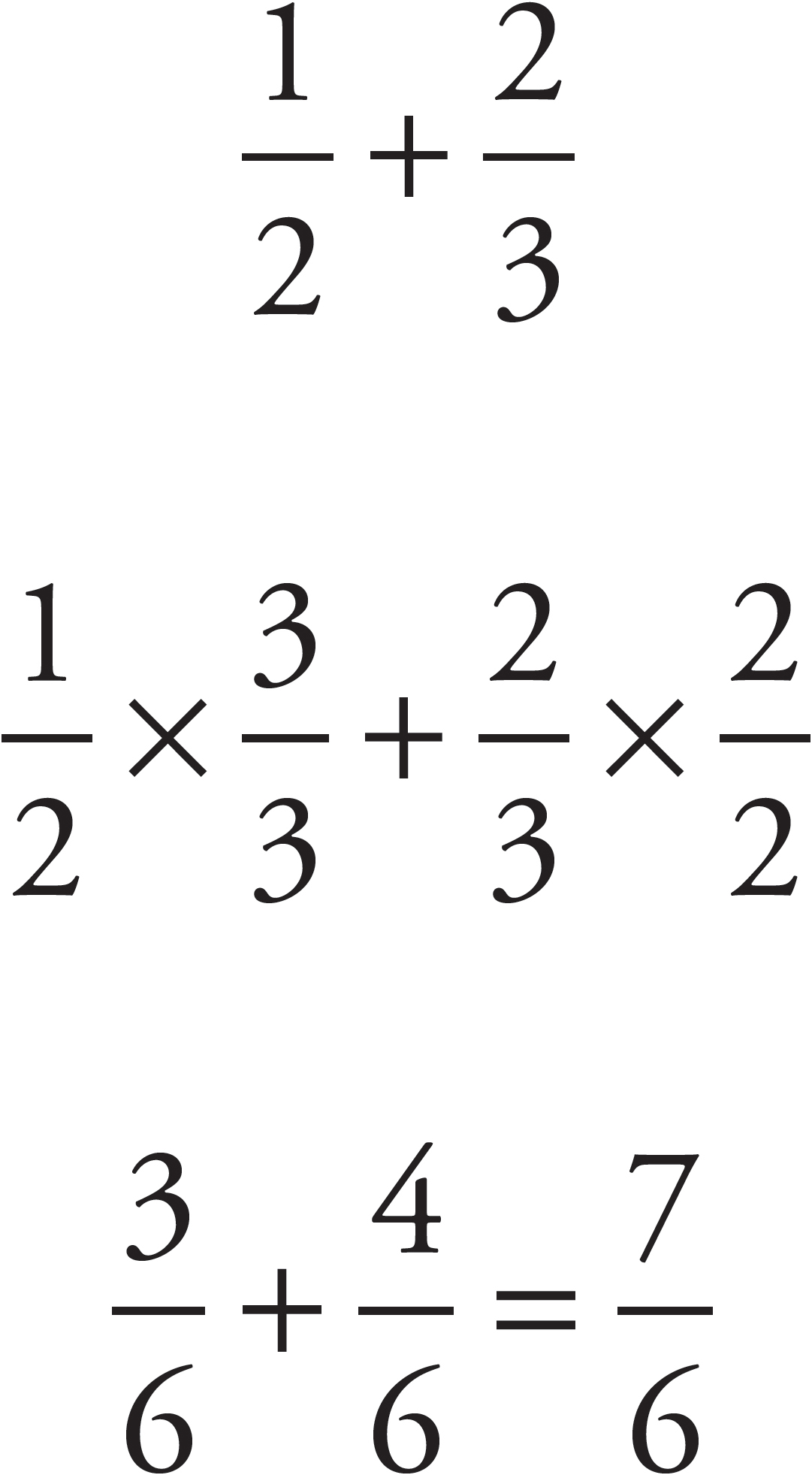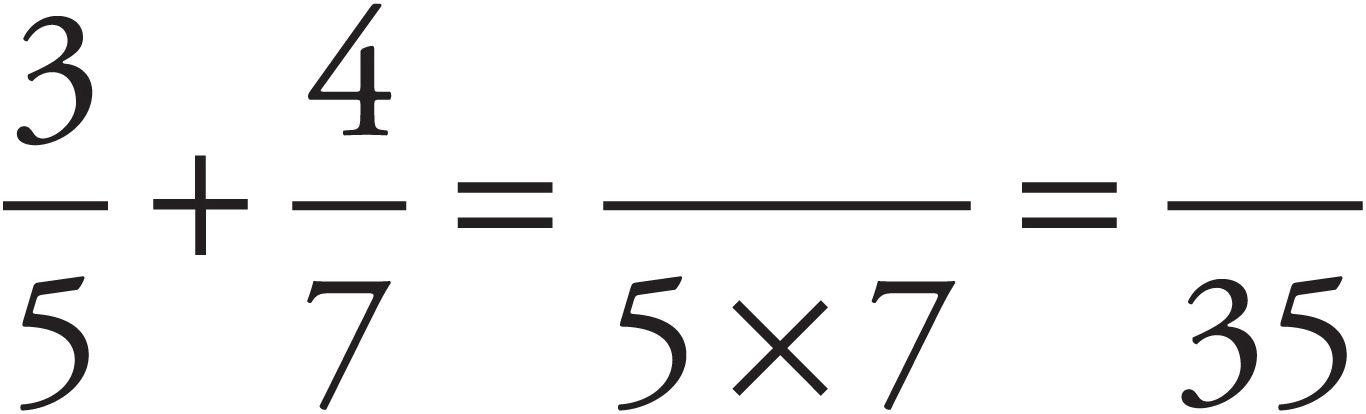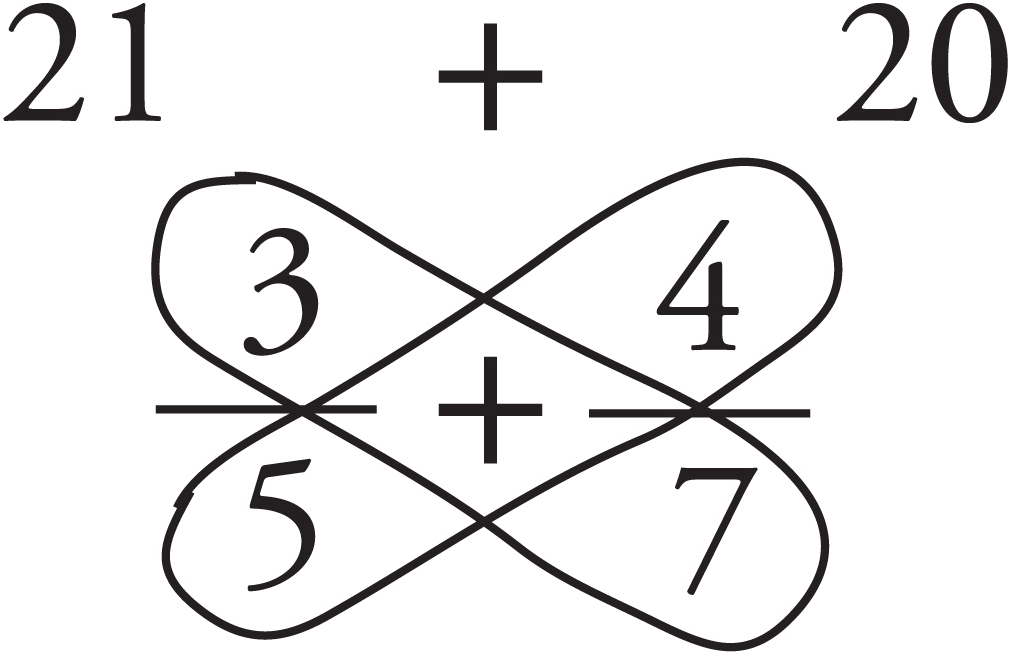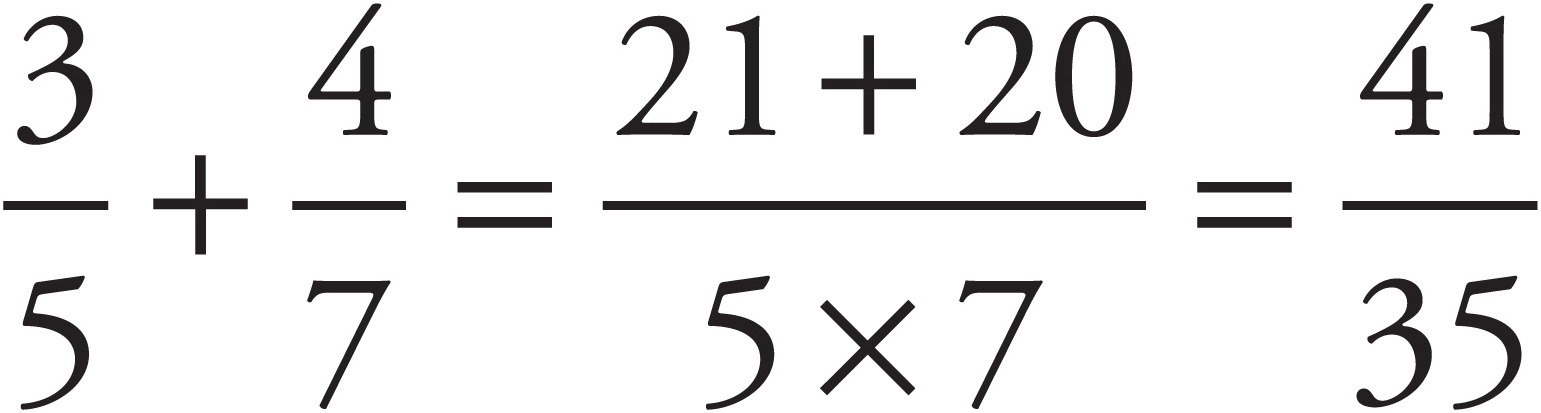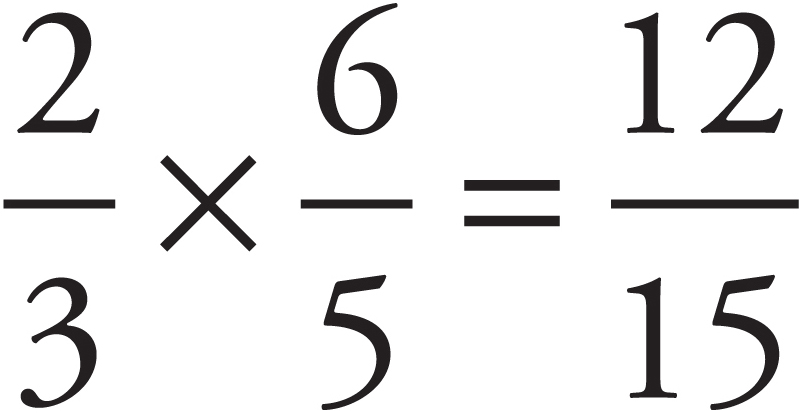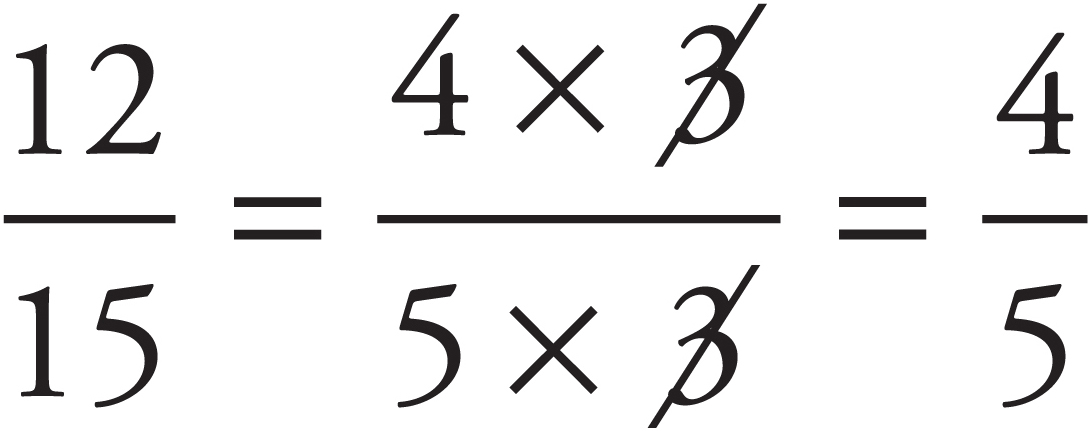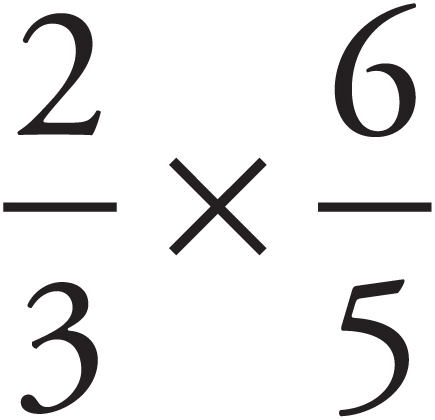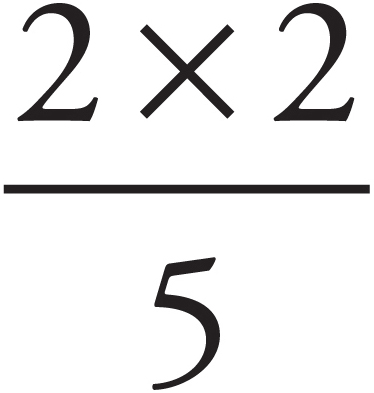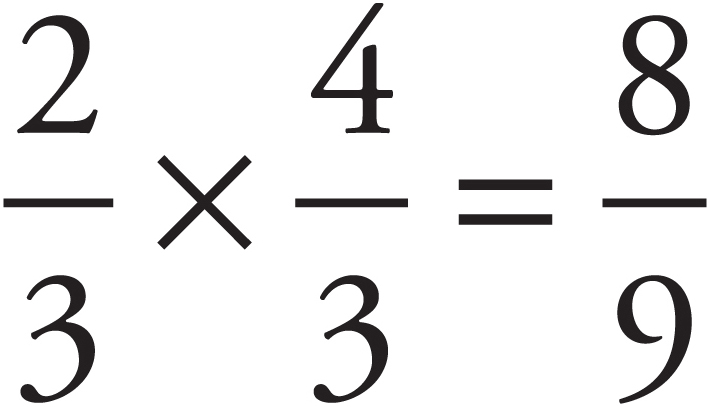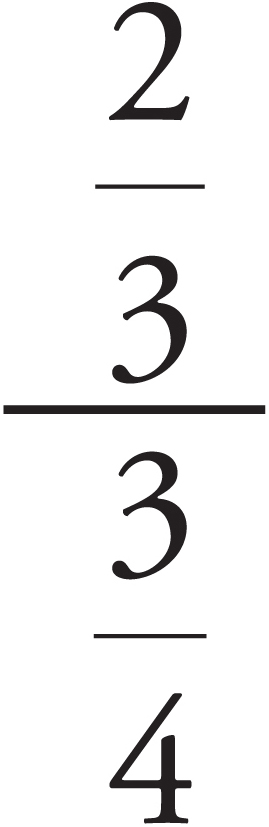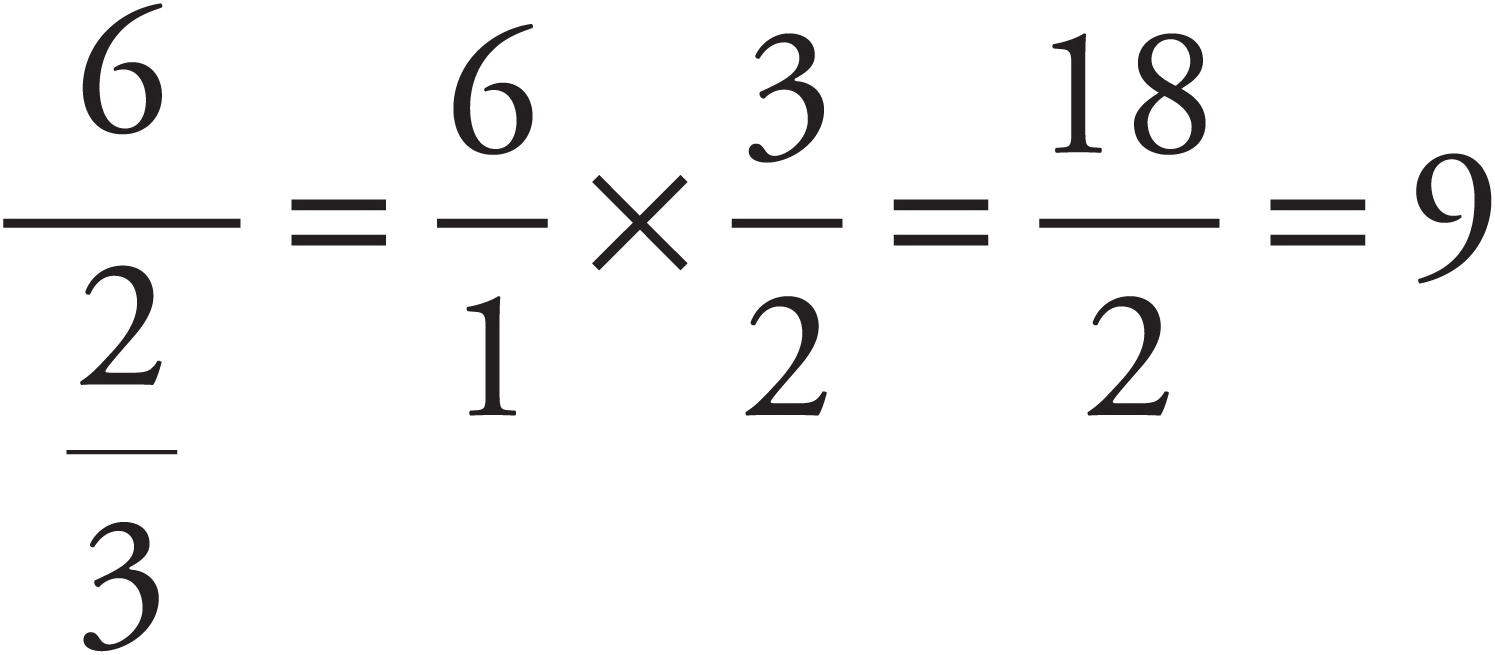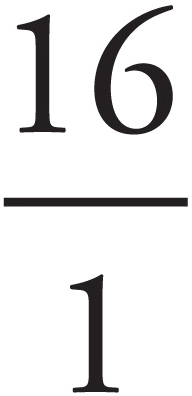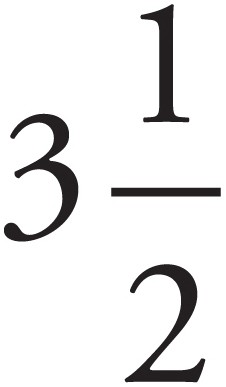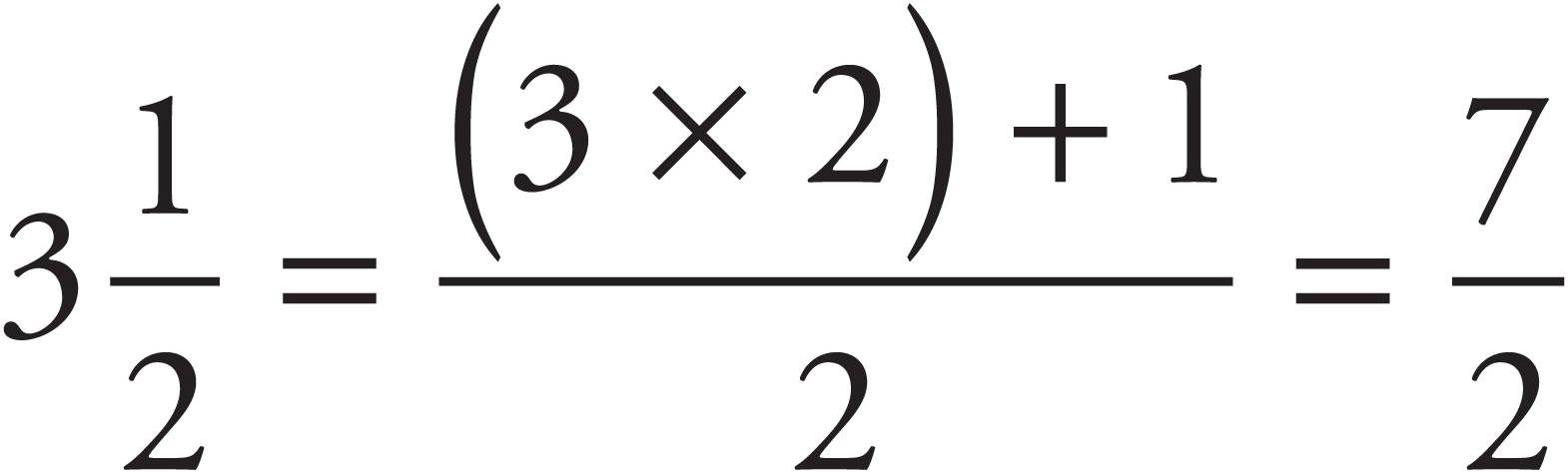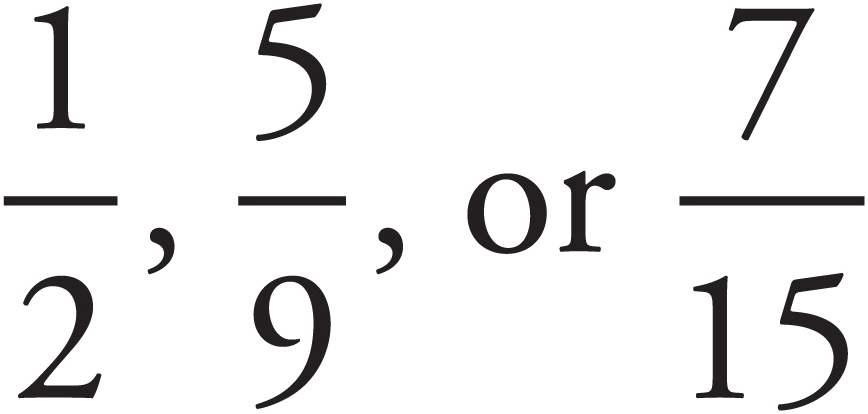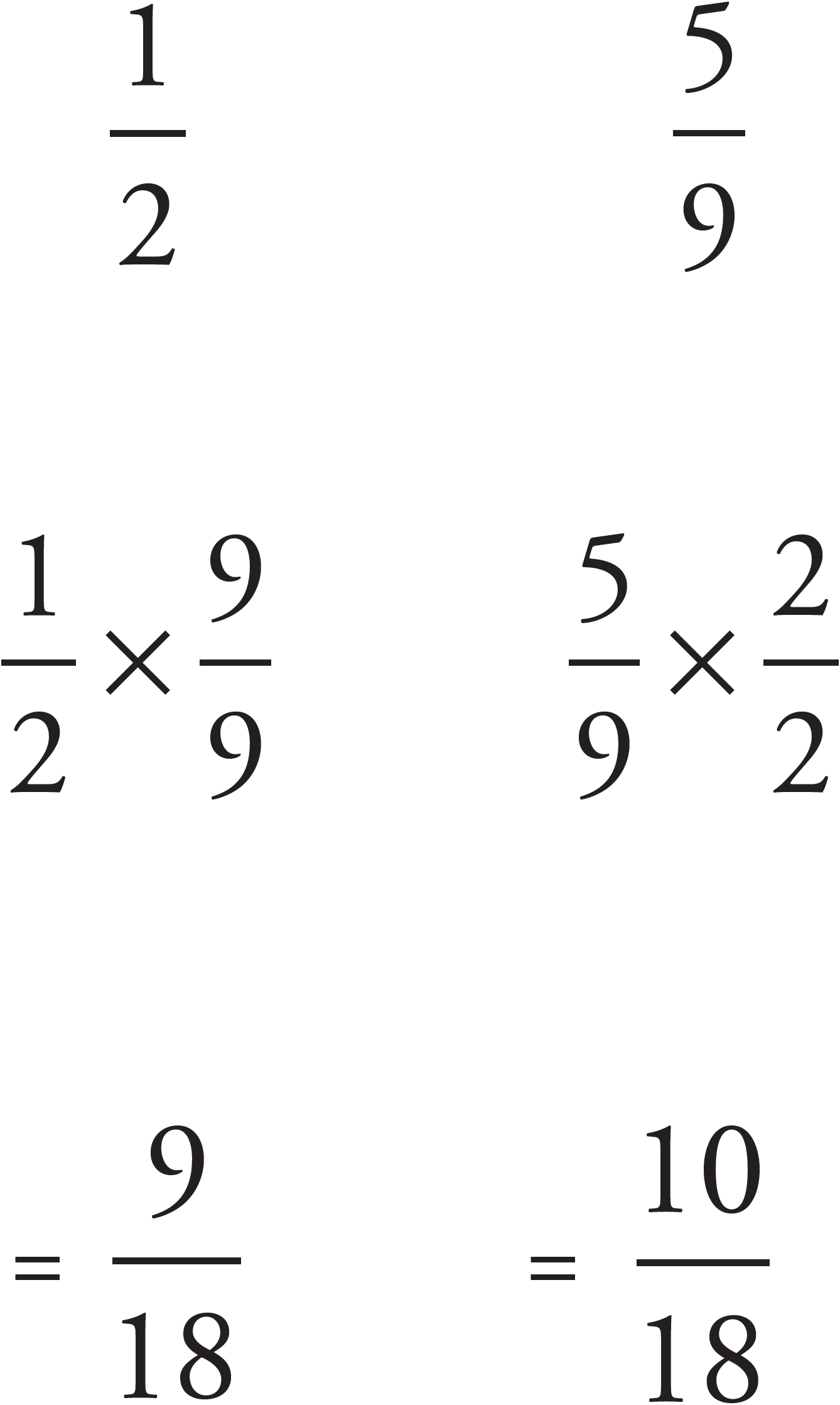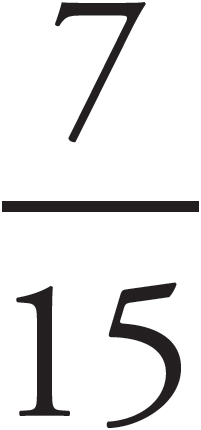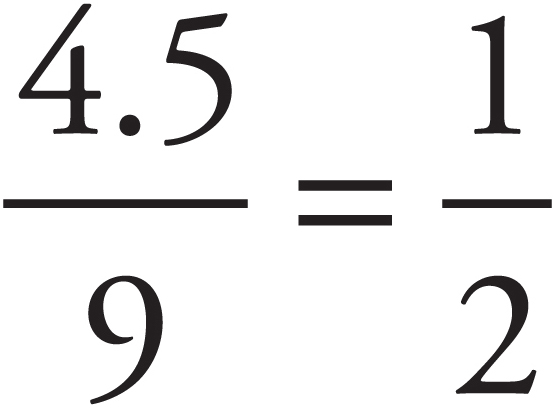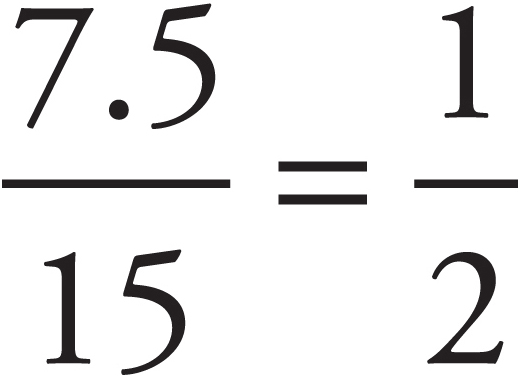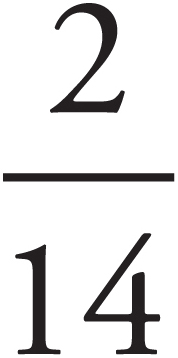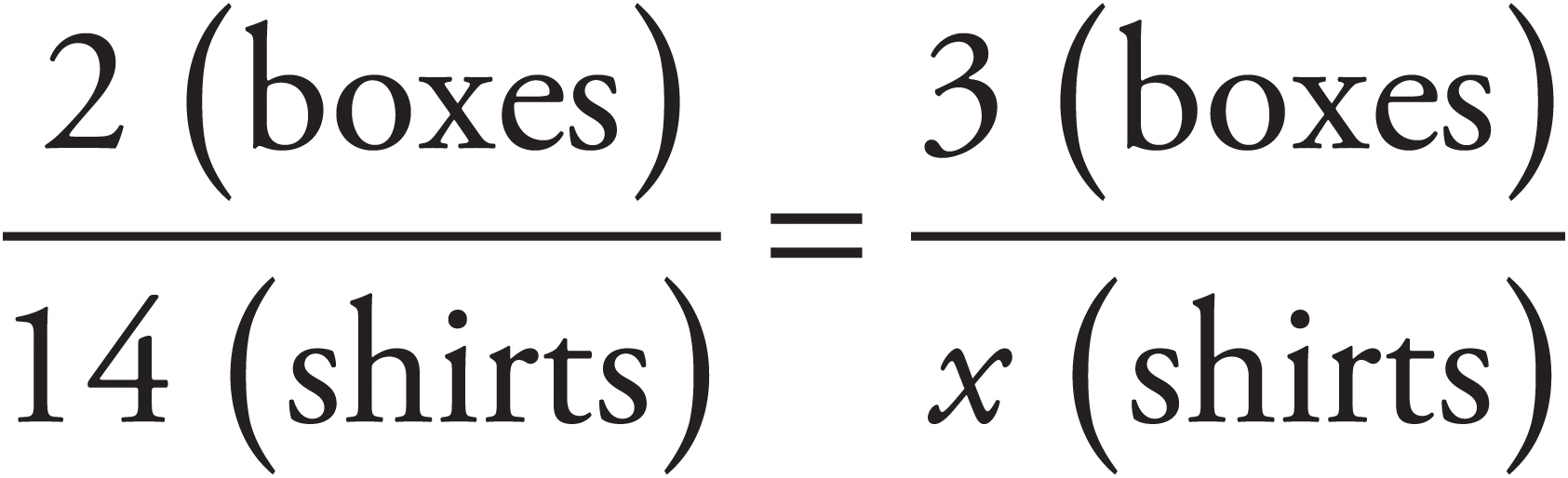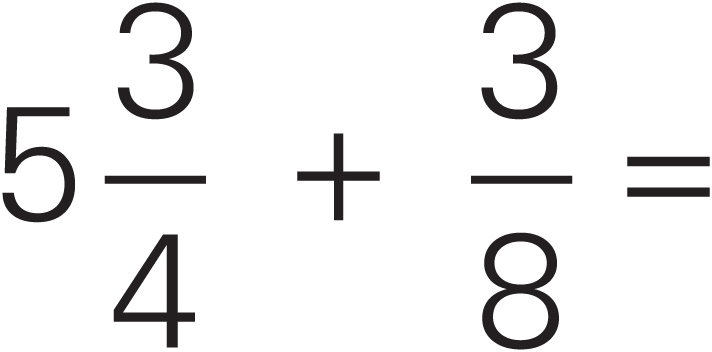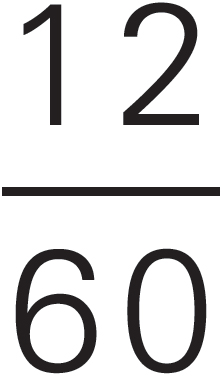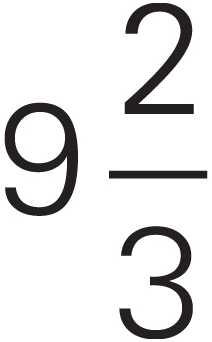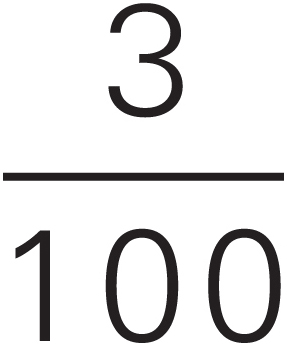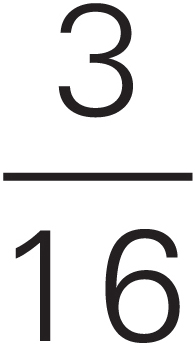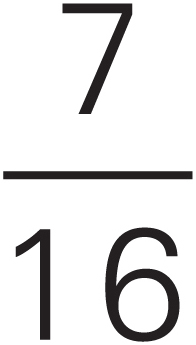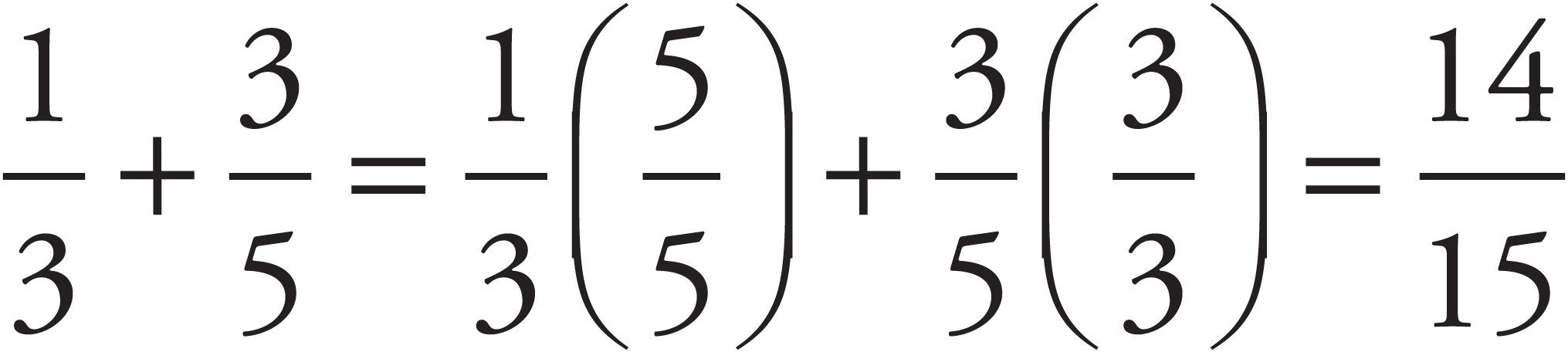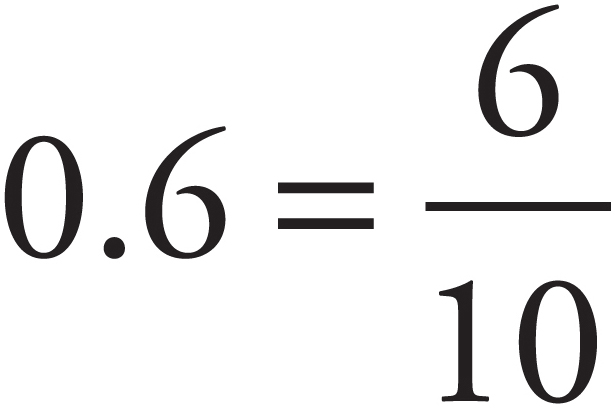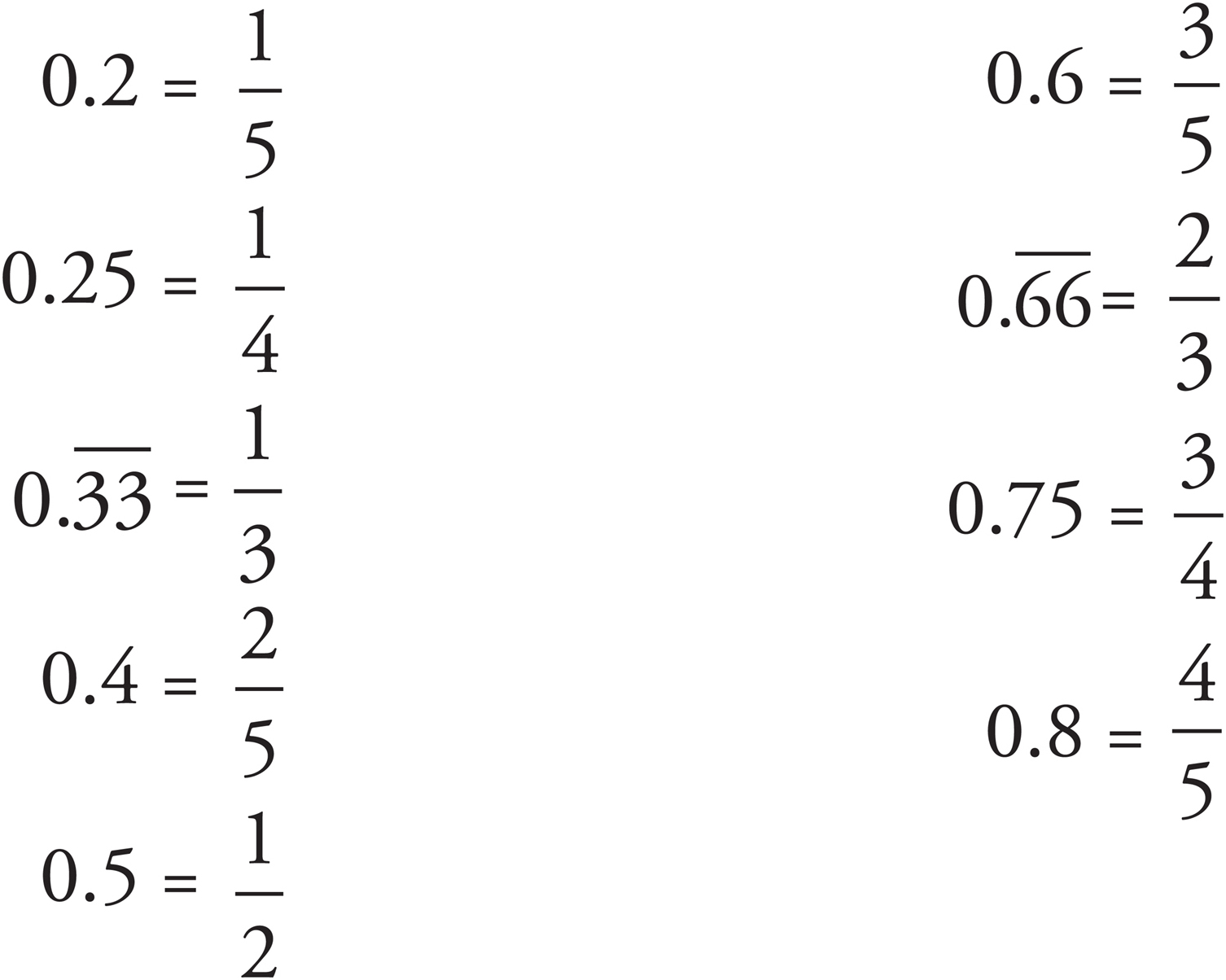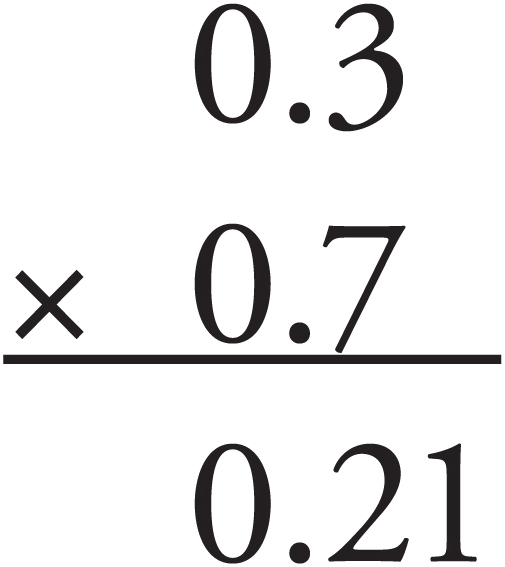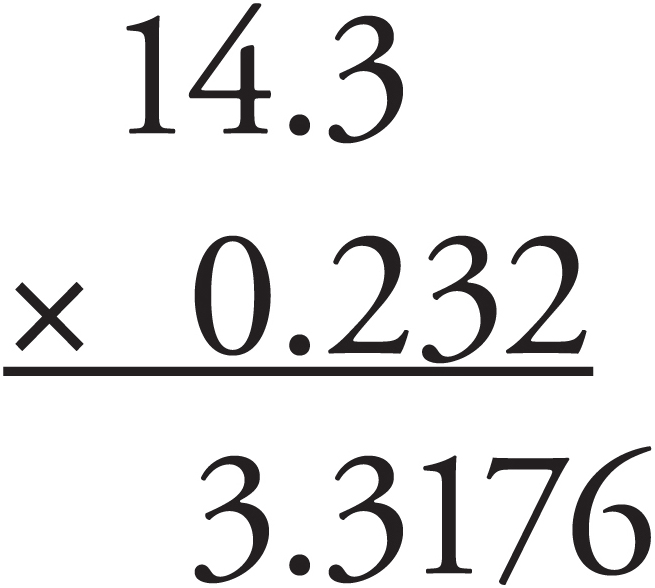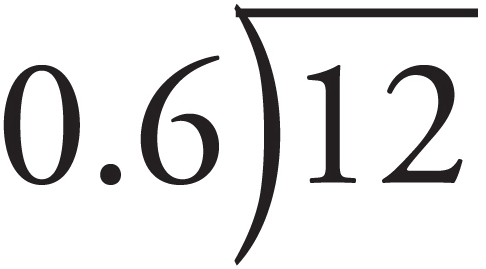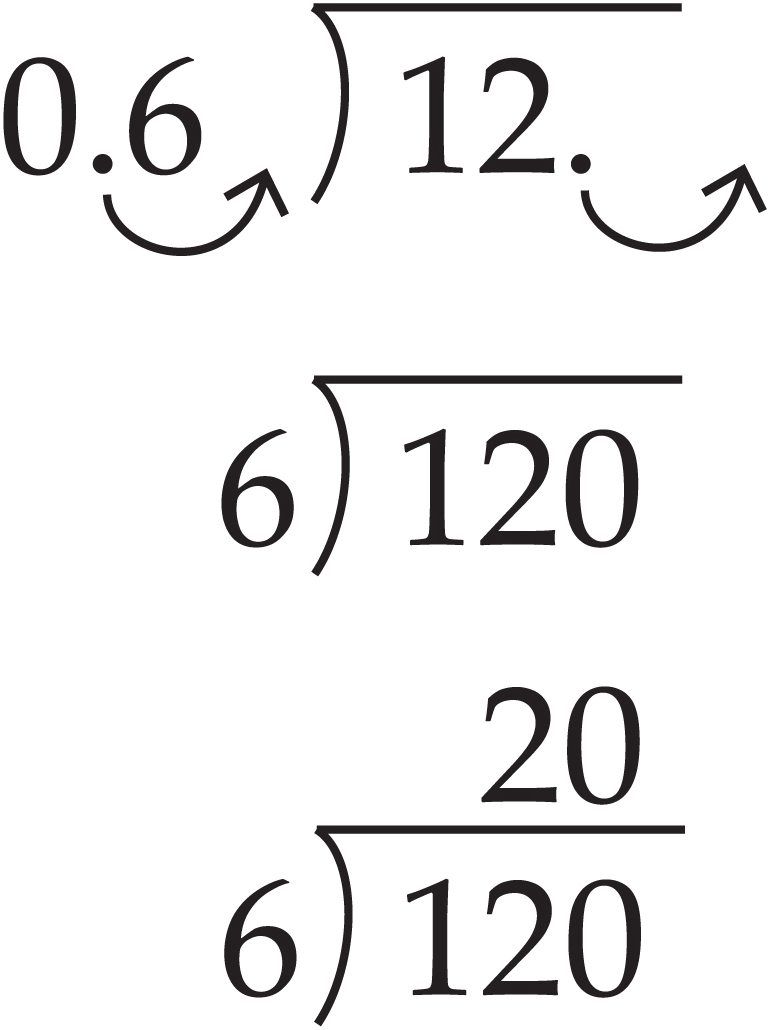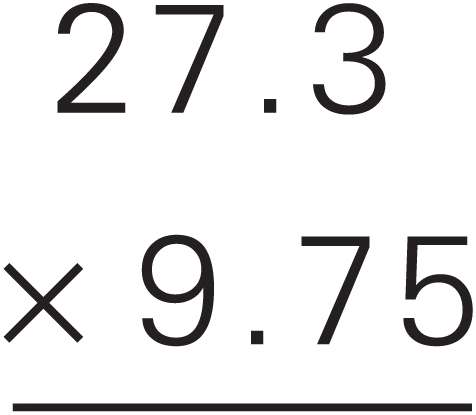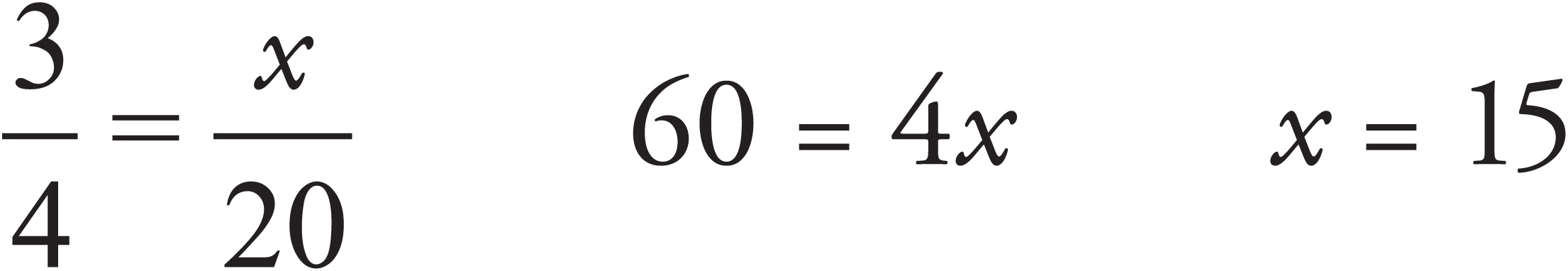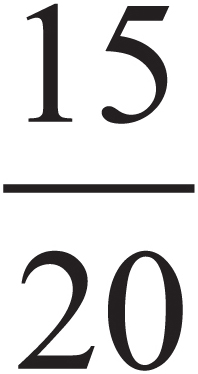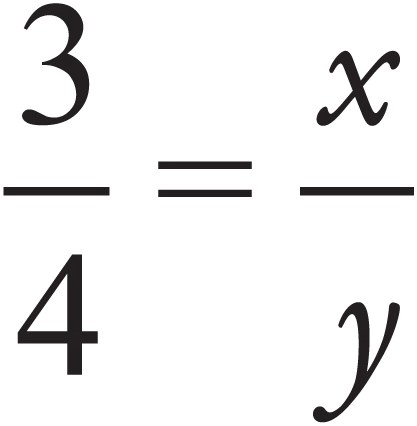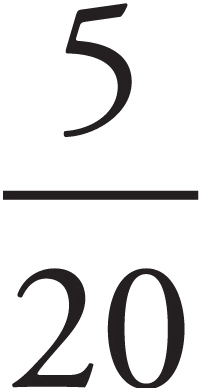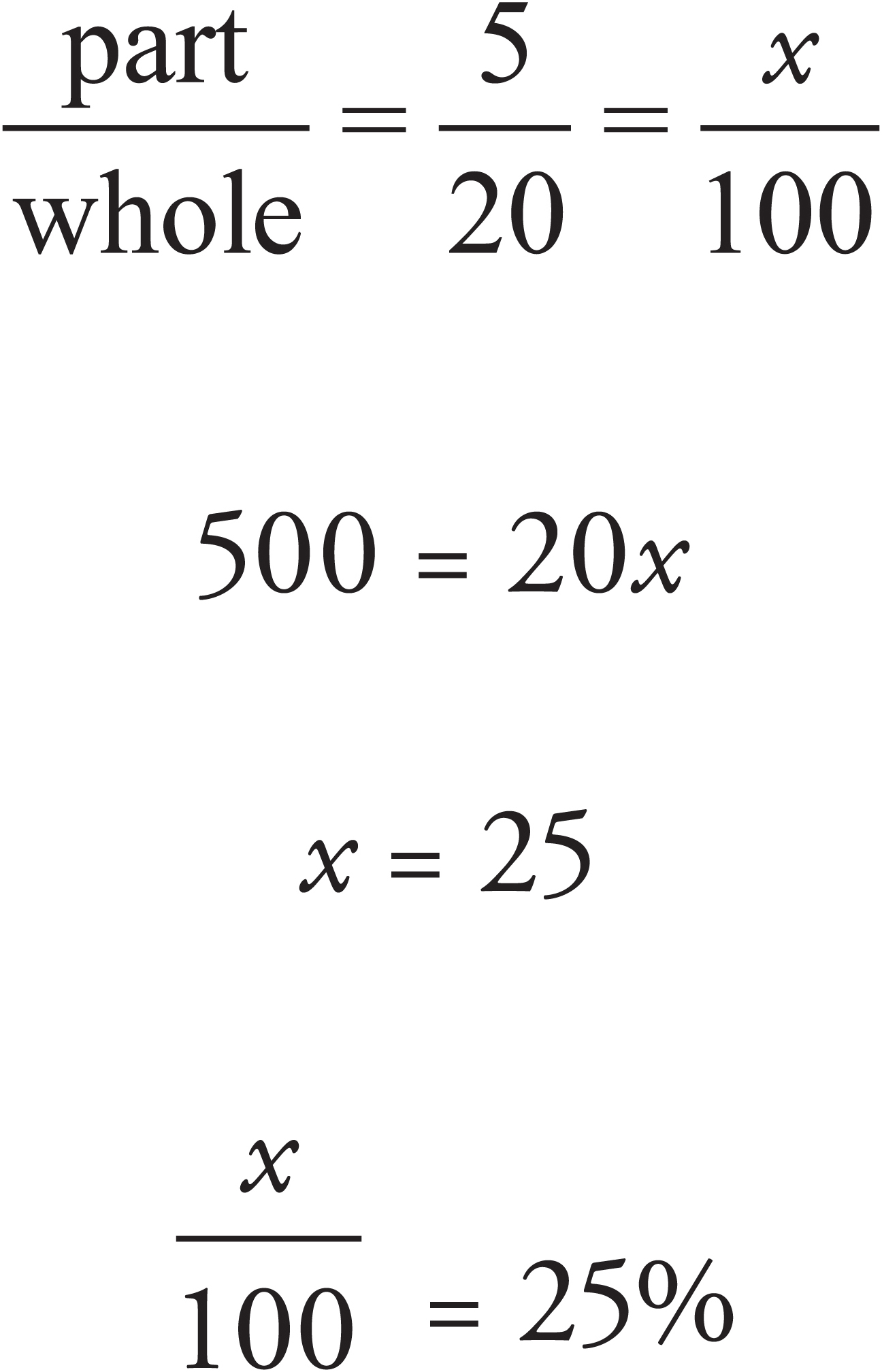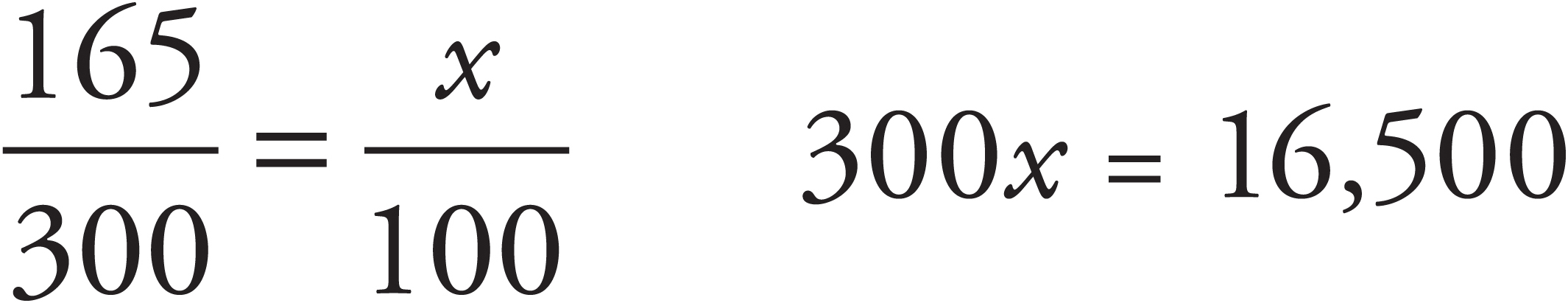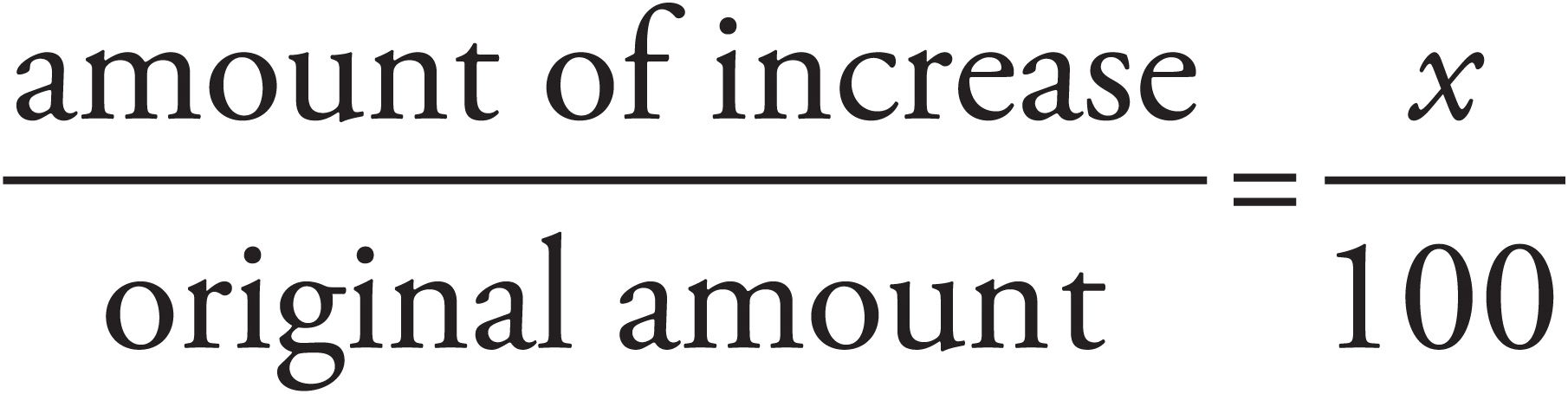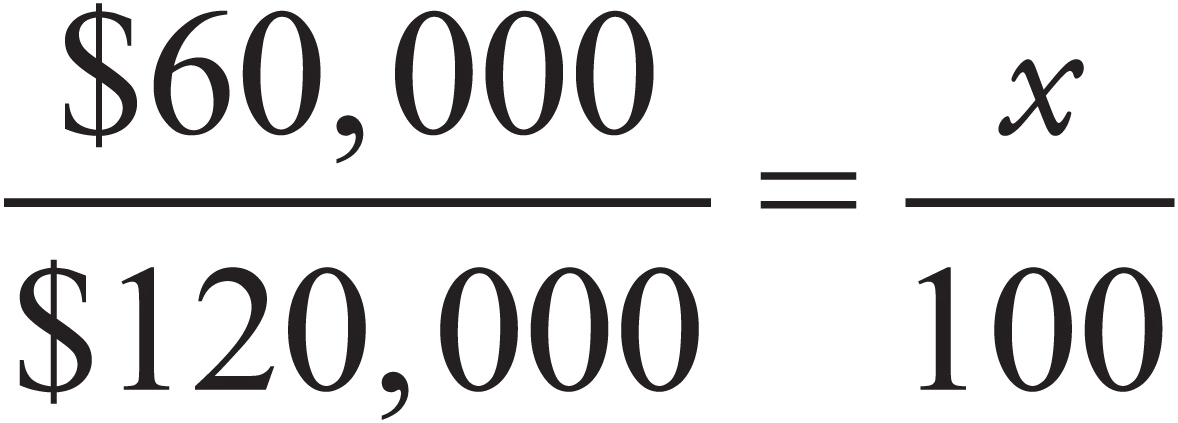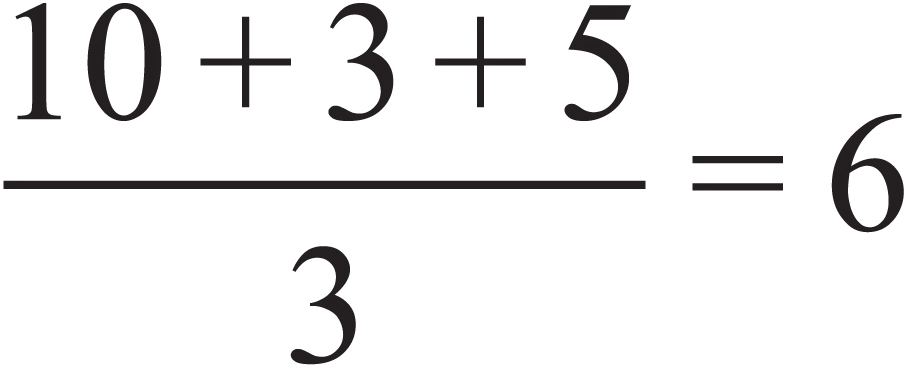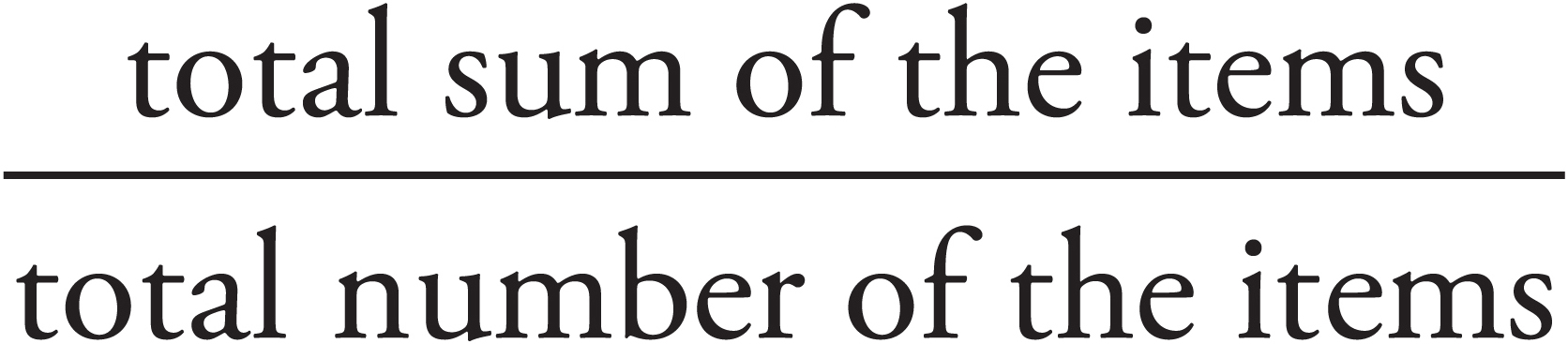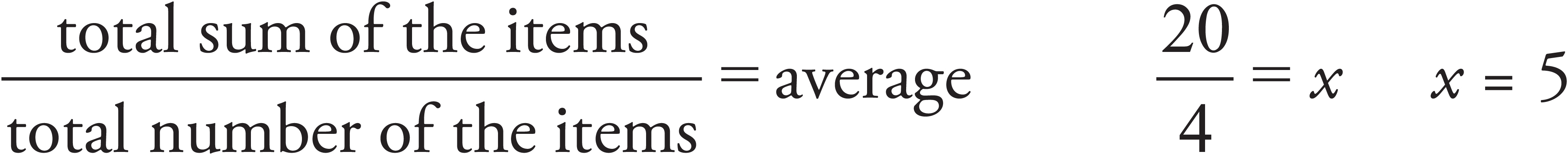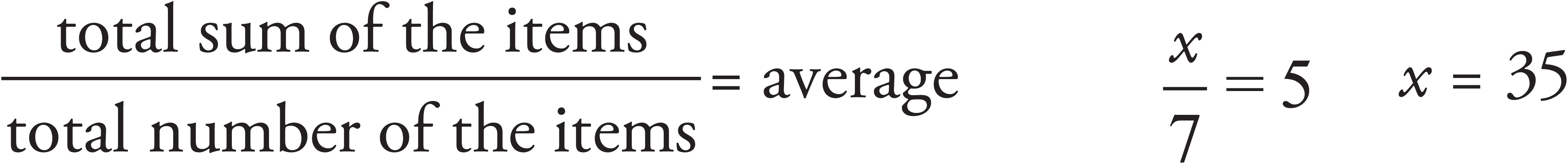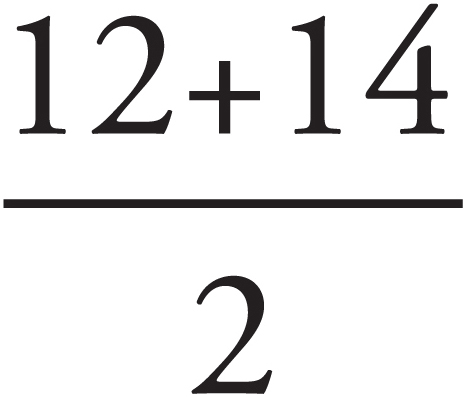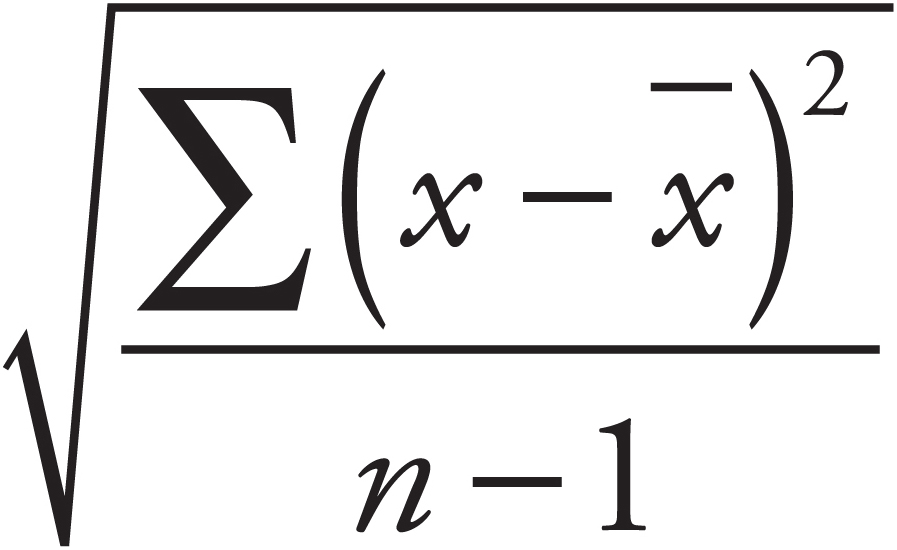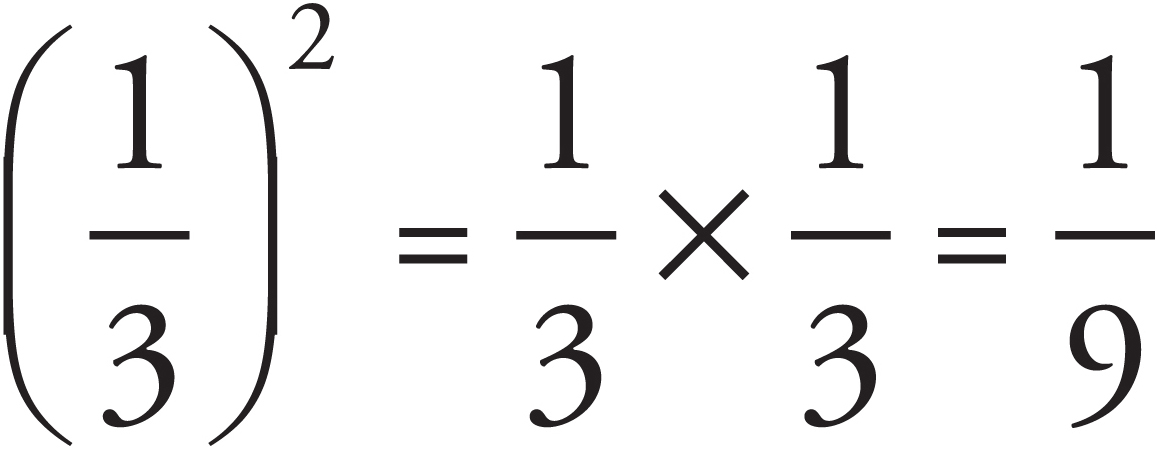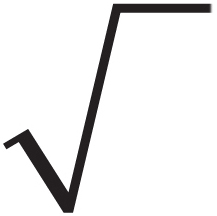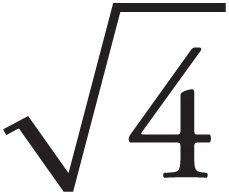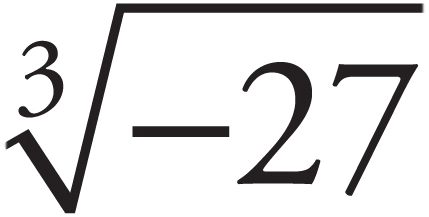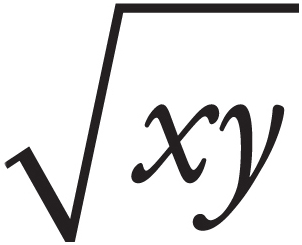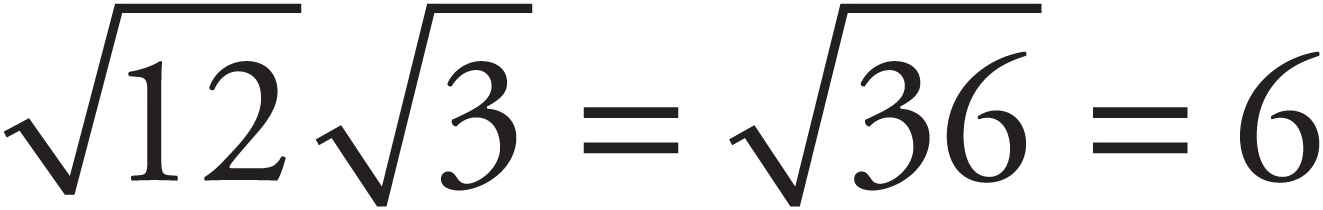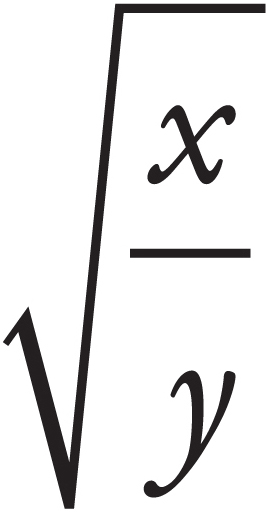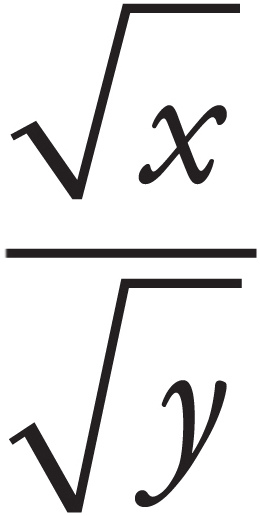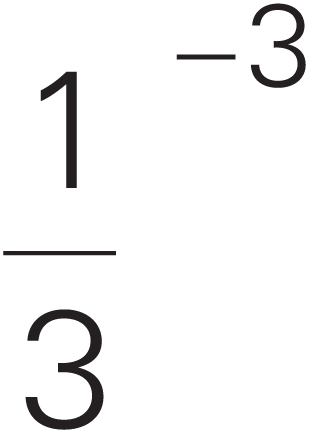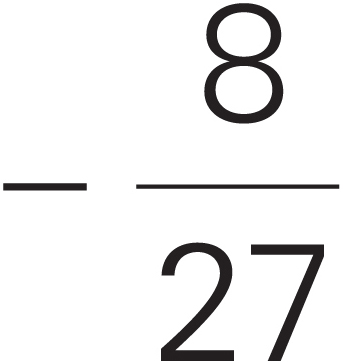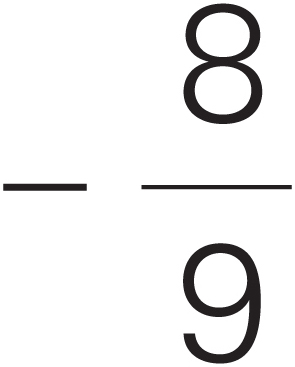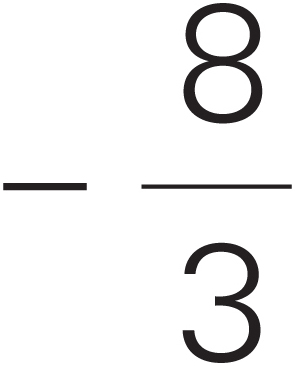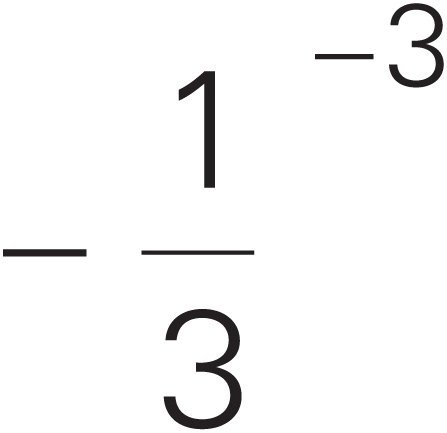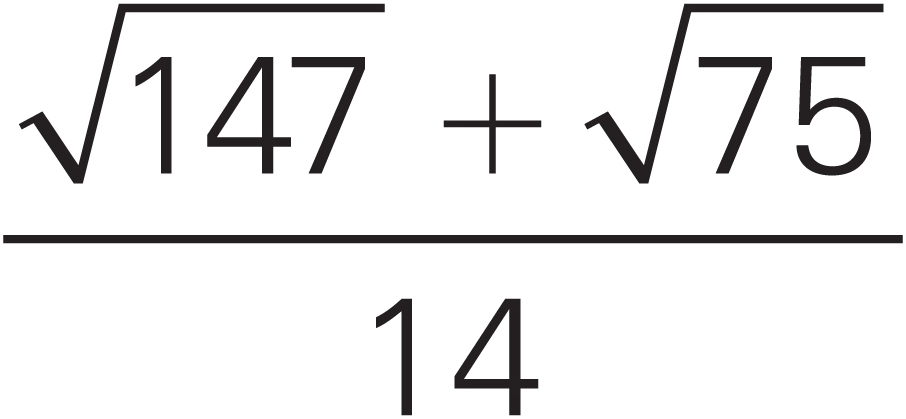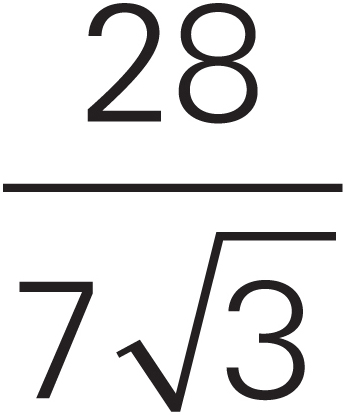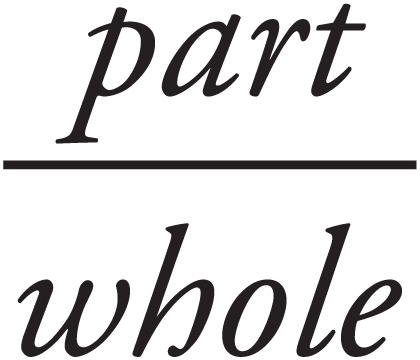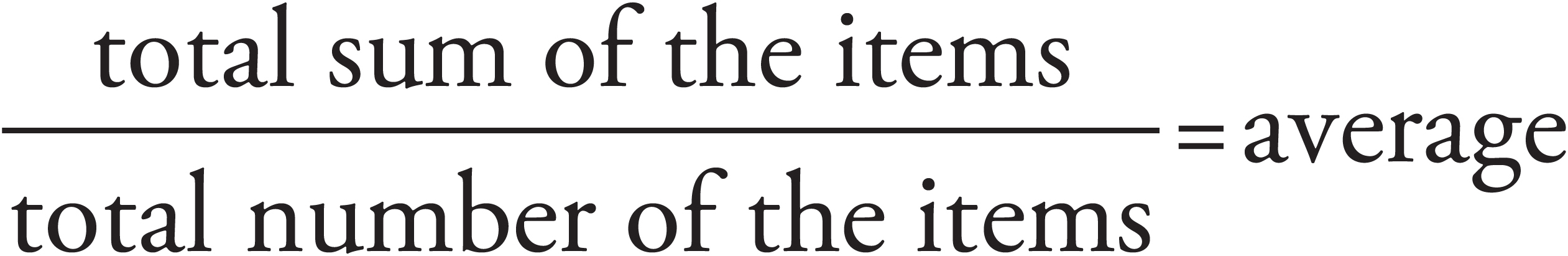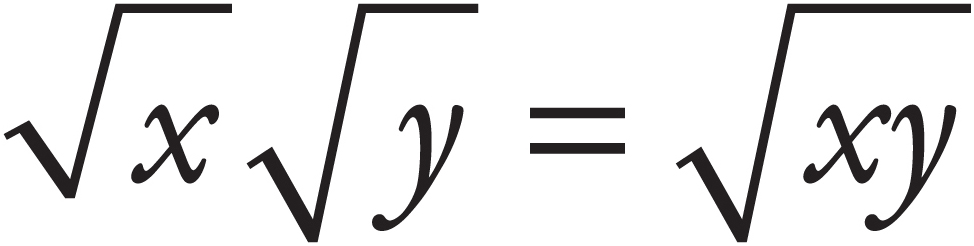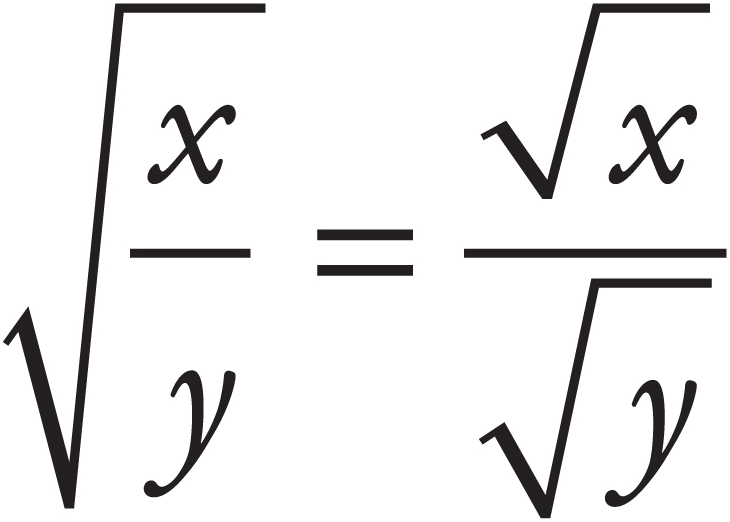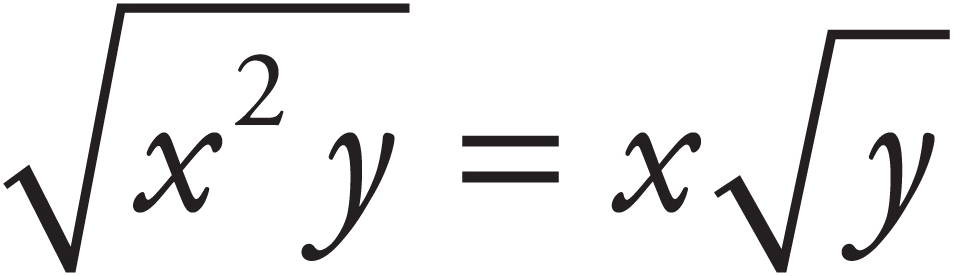Chapter 10
Arithmetic
Do you remember all the rules for exponents? This chapter will review rules for those and other important mathematical concepts and teach you how to solve problems involving fractions, proportions, decimals, ratios, percentages, averages, medians, modes, standard deviation, exponents, and radicals.
Although arithmetic is only one of the three types of math tested on the GMAT, arithmetic problems comprise about half of the total number of math questions.
Here are the specific arithmetic topics tested on the GMAT:
-
Axioms and Fundamentals (properties of integers, positive and negative numbers, even and odd). These were covered in Chapter 7.
-
Arithmetic Operations
-
Fractions
-
Decimals
-
Ratios
-
Percentages
-
Averages
-
Exponents and Radicals
In this chapter, we will first discuss the fundamentals of each topic and then show how the test writers construct questions based on that topic.
ARITHMETIC OPERATIONS
There are six arithmetic operations you will need for the GMAT:
| 1. |
Addition (2 + 2) |
The result of addition is a sum or total. |
| 2. |
Subtraction (6 – 2) |
The result of subtraction is a difference. |
| 3. |
Multiplication (2 × 2) |
The result of multiplication is a product. |
| 4. |
Division (8 ÷ 2) |
The result of division is a quotient. |
| 5. |
Raising to a power (x2) |
In the expression x2, the little 2 is called an exponent.
|
| 6. |
Finding a square root ( ) )
|
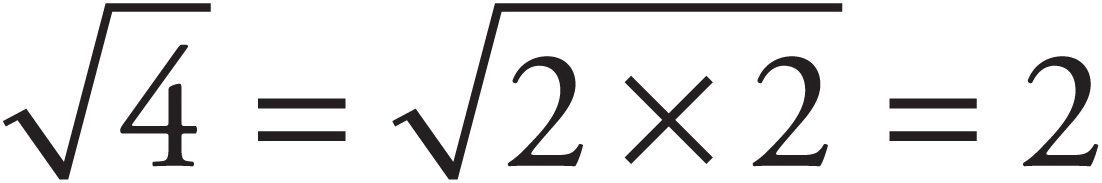 |
Which One Do I Do First?
In a problem that involves several different operations, the operations must be performed in a particular order, and occasionally GMAC likes to see whether you know what that order is. Here’s an easy way to remember the order of operations:
Please Excuse My Dear Aunt Sally
or
PEMDAS
The first letters stand for Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. Do operations that are enclosed in parentheses first; then take care of exponents; then multiply and divide; then add and subtract, going from left to right.
The Drill on Drills
-
You can’t use a calculator on the math section of the GMAT, so please don’t use one as you work through the math drills in this book.
-
To mimic the actual conditions of the test, get used to using scratch paper rather than writing in the book directly.
DRILL 2
Just to get you started, solve each of the following problems by performing the indicated operations in the proper order. The answers can be found in Part VI.
1.74 + (27 – 24) =
2.(8 × 9) + 7 =
3.2(9 – (8 ÷ 2)) =
4.2(7 – 3) + (–4)(5 – 7) =
Here’s an easy question that shows how GMAC might test PEMDAS.
5.4(–3(3 – 5) + 10 – 17) =
 –27
–27
 –4
–4
 –1
–1
 32
32
 84
84
It is not uncommon to see a Data Sufficiency problem like this on the GMAT:
6.What is the value of x ?
(1)x3 = 8
(2)x2 = 4
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are not sufficient.
Statements (1) and (2) TOGETHER are not sufficient.
There are two operations that can be done in any order, provided they are the only operations involved: When you are adding or multiplying a series of numbers, you can group or regroup the numbers any way you like.
2 + 3 + 4 is the same as 4 + 2 + 3
and
4 × 5 × 6 is the same as 6 × 5 × 4
This is called the associative law, but the name will not be tested on the GMAT.
Another law that GMAC likes to test states that
a(b + c) = ab + ac and a(b – c) = ab – ac.
This is called the distributive law but, again, you don’t need to know that for the test. Sometimes the distributive law can provide you with a shortcut to the solution of a problem. If a problem gives you information in “factored form”—a(b + c)—you should distribute it immediately. If the information is given in distributed form—ab + ac—you should factor it.
DRILL 3
If the following problems are in distributed form, factor them; if they are in factored form, distribute them. Then do the indicated operations. Answers are in Part VI.
1.x 2 + x
2.(55 × 12) + (55 × 88)
3.a(b + c – d)
4.abc + xyc
A GMAT problem might look like this:
5.If x = 6 what is the value of 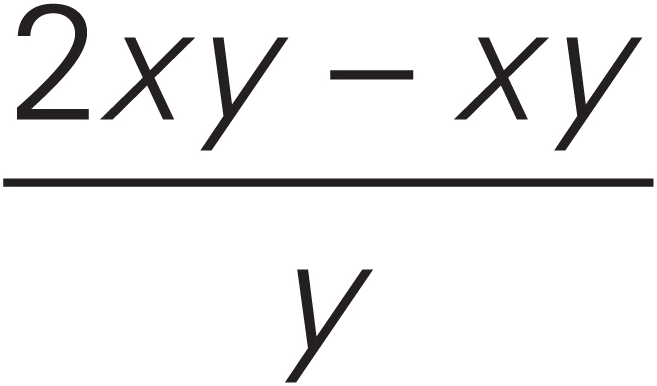 ?
?
 –30
–30
 6
6
 8
8
 30
30
 It cannot be determined from the information given.
It cannot be determined from the information given.
It is not uncommon to see a Data Sufficiency problem like this on the GMAT:
6.If ax + ay + az = 15, what is x + y + z ?
(1) x = 2
(2) a = 5
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are not sufficient.
Statements (1) and (2) TOGETHER are not sufficient.
A device calculates the worth of gem stones based on quality such that a gem with a quality rating of q – 1 is worth 5 times more than a gem with a quality rating of q. According to this device, the worth of a gem with a quality rating of p – r is how many times greater than that of a gem with a rating of p ?
 p5 – r5
p5 – r5
 r5
r5
 (p – r)5
(p – r)5
 5r
5r
 5r
5r
FRACTIONS
Fractions can be thought of in two ways:
Adding and Subtracting Fractions with the Same Denominator
To add two or more fractions that have the same denominator, simply add up the numerators and put the sum over the common denominator. For example:
Subtraction works exactly the same way:
Adding and Subtracting Fractions with Different Denominators
Before you can add or subtract two or more fractions with different denominators, you must give all of them the same denominator. To do this, multiply the numerator and denominator of each fraction by a number that will give it a denominator in common with the others. If you multiplied each fraction by any old number, the fractions wouldn’t have their original values, so the number you multiply by has to be equal to 1. For example, if you wanted to change  into sixths, you could do the following:
into sixths, you could do the following:
We haven’t actually changed the value of the fraction, because  equals 1.
equals 1.
If we wanted to add:
The Bowtie
The Bowtie method has been a staple of The Princeton Review’s materials since the company began in a living room in New York City in 1981. It’s been around so long because it works so simply.
To add  and
and  , for example, follow these three steps:
, for example, follow these three steps:
Step One: Multiply the denominators together to form the new denominator.
Step Two: Multiply the first denominator by the second numerator (5 × 4 = 20) and the second denominator by the first numerator (7 × 3 = 21) and place these numbers above the fractions, as shown below.
Step Three: Add the products to form the new numerator.
Subtraction works the same way.
Note that with subtraction, the order of the numerators is important. The new numerator is 21 – 20, or 1. If you somehow get your numbers reversed and use 20 – 21, your answer will be  , which is incorrect. One way to keep your subtraction straight is to always multiply up from denominator to numerator when you use the Bowtie.
, which is incorrect. One way to keep your subtraction straight is to always multiply up from denominator to numerator when you use the Bowtie.
Multiplying Fractions
To multiply fractions, just multiply the numerators and put the product over the product of the denominators. For example:
Reducing Fractions
When you add or multiply fractions, you often end up with a big fraction that is hard to work with. You can usually reduce such a fraction. To reduce a fraction, find a factor of the numerator that is also a factor of the denominator. It saves time to find the biggest factor they have in common, but this isn’t critical. You may just have to repeat the process a few times. When you find a common factor, cancel it. For example, let’s take the product we just found when we multiplied the fractions above:
Get used to reducing all fractions (if they can be reduced) before you do any work with them. It saves a lot of time and prevents errors in computation.
For example, in that last problem, we had to multiply two fractions together:
Before you multiplied 2 × 6 and 3 × 5, you could have reduced  ×
×  =
=  =
= 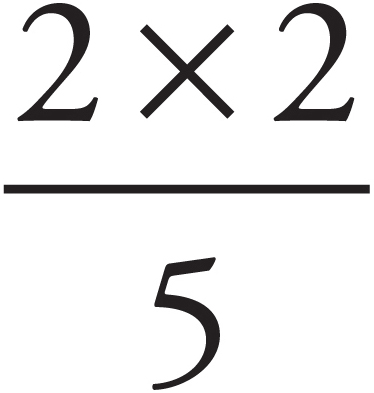 =
=  .
.
Dividing Fractions
To divide one fraction by another, just invert the second fraction and multiply:
which is the same thing as…
You may see this same operation written like this:
Again, just invert and multiply. This next example is handled the same way:
When you invert a fraction, the new fraction is called a reciprocal.  is the reciprocal of
is the reciprocal of  . The product of two reciprocals is always 1.
. The product of two reciprocals is always 1.
Converting to Fractions
An integer can be expressed as a fraction by making the integer the numerator and 1 the denominator: 16 = 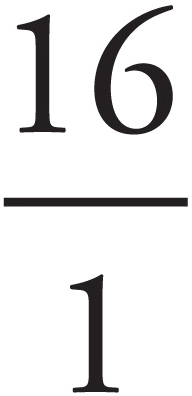 .
.
The GMAT sometimes gives you numbers that are mixtures of integers and fractions, for example, 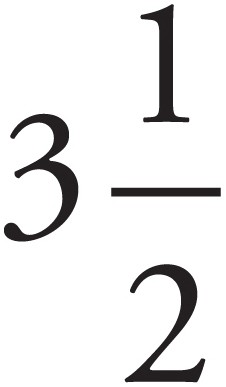 . It’s easier to work with these numbers if you convert them into fractions. Simply multiply the denominator by the integer, then add the numerator, and place the resulting number over the original denominator.
. It’s easier to work with these numbers if you convert them into fractions. Simply multiply the denominator by the integer, then add the numerator, and place the resulting number over the original denominator.
Comparing Fractions
In the course of a problem, you may have to compare two or more fractions and determine which is greater. This is easy to do as long as you remember that you can compare fractions directly only if they have the same denominator. Suppose you had to decide which of these three fractions is greatest:
To compare these fractions directly, you need a common denominator, but finding a common denominator that works for all three fractions would be complicated and time consuming. It makes more sense to compare these fractions two at a time. We showed you the classical way to find common denominators when we talked about adding fractions earlier.
Let’s start with  and
and  . An easy common denominator for these two fractions is 18 (9 × 2).
. An easy common denominator for these two fractions is 18 (9 × 2).
Because  is greater, let’s compare it with
is greater, let’s compare it with 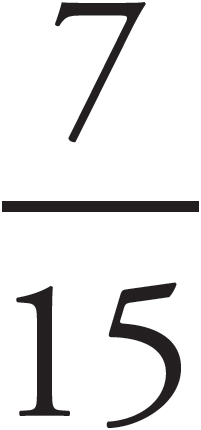 . Here the easiest common denominator is 45. But before we do that…
. Here the easiest common denominator is 45. But before we do that…
Two Shortcuts
Comparing fractions is another situation where we can use the Bowtie. The idea is that if all you need to know is which fraction is greater, you just have to compare the new numerators. Again, simply multiply the denominator of the first fraction by the numerator of the second and the denominator of the second by the numerator of the first, as shown here.
You could also have saved yourself some time on the last problem by a little fast estimation. Again, which is greater?  ,
,  , or
, or 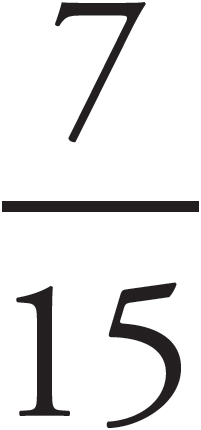 ?
?
Let’s think about  in terms of
in terms of  . How many ninths equal a half? To put it another way, what is half of 9? 4.5. So
. How many ninths equal a half? To put it another way, what is half of 9? 4.5. So 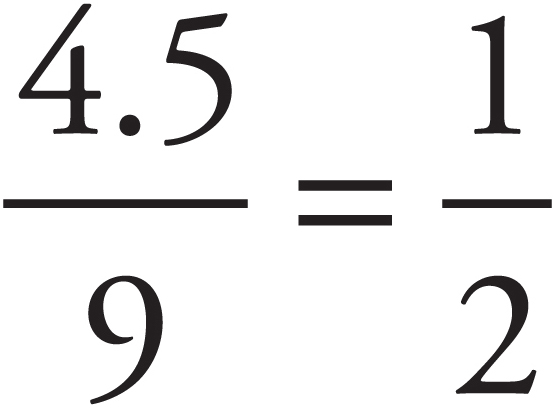 . That means
. That means  is greater than
is greater than  .
.
Now let’s think about 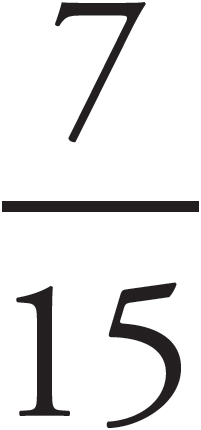 . Half of 15 is 7.5.
. Half of 15 is 7.5. 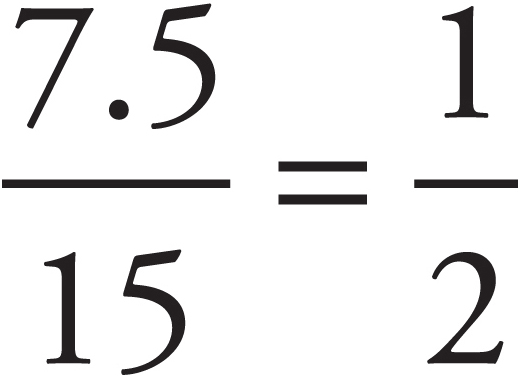 , which means that
, which means that 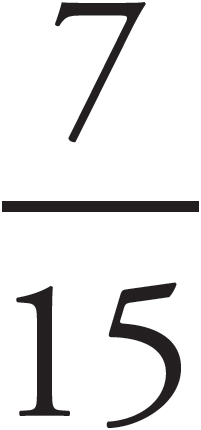 is less than
is less than  .
.
PROPORTIONS
A fraction can be expressed in many ways.  also equals
also equals  or
or  , etc. A proportion is just a different way of expressing a fraction. Here’s an example:
, etc. A proportion is just a different way of expressing a fraction. Here’s an example:
If 2 boxes hold a total of 14 shirts, how many shirts are contained in 3 boxes?
Here’s How to Crack It
The number of shirts per box can be expressed as a fraction. What you’re asked to do is express the fraction 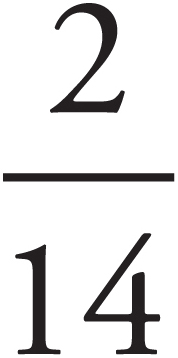 in a different way.
in a different way.
To find the answer, all you need to do is find a value for x such that 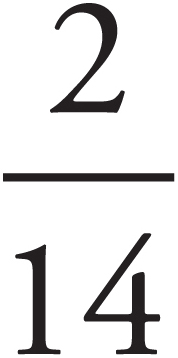 =
=  . The easiest way to do this is to cross-multiply.
. The easiest way to do this is to cross-multiply.
2x = 42, which means that x = 21. There are 21 shirts in 3 boxes.
DRILL 4
The answers to these questions can be found in Part VI.
1.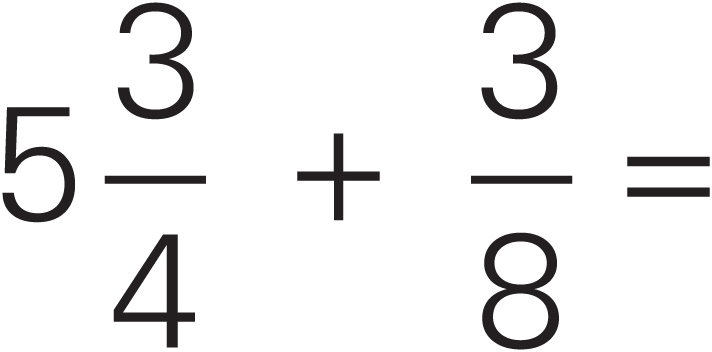
2.Reduce 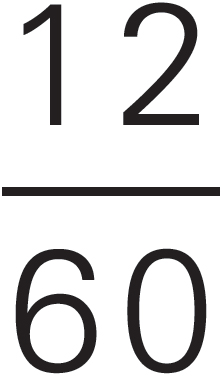
3.Convert 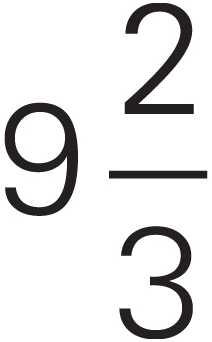 to a fraction
to a fraction
4.
A relatively easy GMAT fraction problem might look like this:
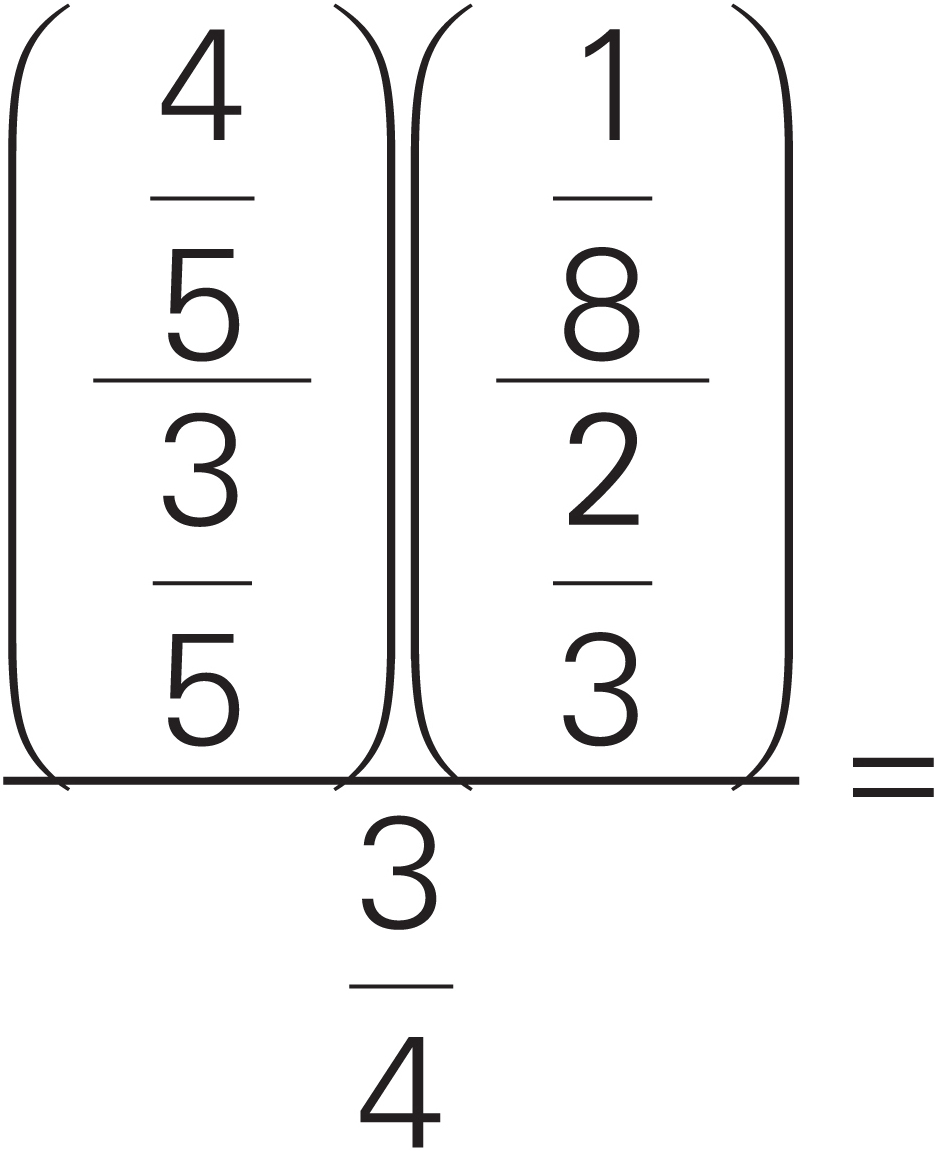
5.

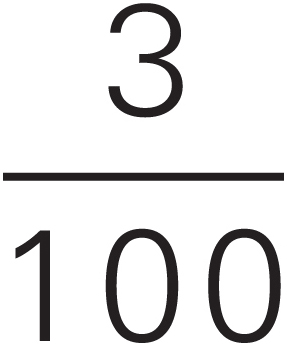

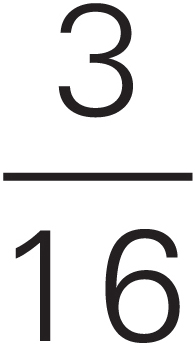


 1
1

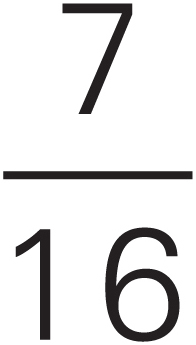
Fractions: Advanced Principles
Now that you’ve been reacquainted with the basics of fractions, let’s go a little further. More complicated fraction problems usually involve all of the rules we’ve just mentioned, with the addition of two concepts: 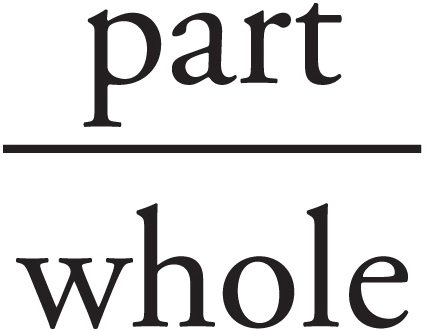 , and the rest. Here’s a typical medium fraction problem:
, and the rest. Here’s a typical medium fraction problem:
A cement mixture is composed of 3 elements. By weight,  of the mixture is sand,
of the mixture is sand,  of the mixture is water, and the remaining 12 pounds of the mixture is gravel. What is the weight of the entire mixture in pounds?
of the mixture is water, and the remaining 12 pounds of the mixture is gravel. What is the weight of the entire mixture in pounds?
 4
4
 8
8
 36
36
 60
60
 180
180
Easy Eliminations
Before we even start doing serious math, let’s use some common sense. The weight of the gravel alone is 12 pounds. Because we know that sand and water make up the bulk of the mixture—sand  , water
, water  (which is a bit more than half)—the entire mixture must weigh a great deal more than 12 pounds. Choices (A) and (B) are out of the question. Eliminate them.
(which is a bit more than half)—the entire mixture must weigh a great deal more than 12 pounds. Choices (A) and (B) are out of the question. Eliminate them.
Here’s How to Crack It
The difficulty in solving this problem is that sand and water are expressed as fractions, while gravel is expressed in pounds. At first there seems to be no way of knowing what fractional part of the mixture the 12 pounds of gravel represent; nor do we know how many pounds of sand and water there are.
The first step is to add up the fractional parts that we do have:
Sand and water make up 14 parts out of the whole of 15. This means that gravel makes up what is left over—the rest: 1 part out of the whole of 15. Now the problem is simple. Set up a proportion between parts and weights.
Cross-multiply: x = 180. The answer is (E).
DECIMALS ARE REALLY FRACTIONS
A decimal can be expressed as a fraction, and a fraction can be expressed as a decimal.
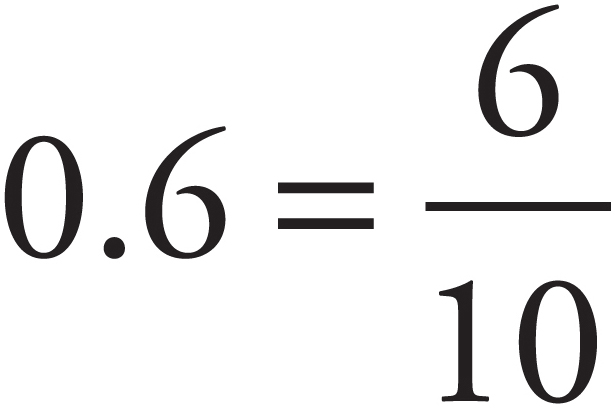 , which can be reduced to
, which can be reduced to 
 is the same thing as 3 ÷ 5
is the same thing as 3 ÷ 5
Which would you rather figure out—the square of  or the square of 0.25? There may be a few of you out there who’ve had so much practice with decimals in your work that you prefer decimals to fractions, but for the rest of us, fractions are infinitely easier to deal with.
or the square of 0.25? There may be a few of you out there who’ve had so much practice with decimals in your work that you prefer decimals to fractions, but for the rest of us, fractions are infinitely easier to deal with.
Occasionally, you will have to work with decimals. Whenever possible, however, convert decimals to fractions. It will save time and eliminate careless mistakes. In fact, it makes sense to memorize the fractional equivalent of some commonly used decimals:
Adding and Subtracting Decimals
To add or subtract decimals, just line up the decimal points and proceed as usual. Adding 6, 2.5, and 0.3 looks like this:
Multiplying Decimals
To multiply decimals, simply ignore the decimal points and multiply the two numbers. When you’ve finished, count all the digits that were to the right of the decimal points in the original numbers you multiplied. Now place the decimal point in your answer so that there are the same number of digits to the right of it. Here are two examples:
There were a total of two digits to the right of the decimal point in the original numbers, so we place the decimal so that there are two digits to the right in the answer.
There were a total of four digits to the right of the decimal point in the original numbers, so we place the decimal such that there are four digits to the right in the answer.
Dividing Decimals
The best way to divide one decimal by another is to convert the number you are dividing by (in mathematical terminology, the divisor) into a whole number. You do this simply by moving the decimal point as many places as necessary. This works as long as you remember to move the decimal point in the number that you are dividing (in mathematical terminology, the dividend) the same number of spaces.
For example, to divide 12 by 0.6, set it up the way you would an ordinary division problem: 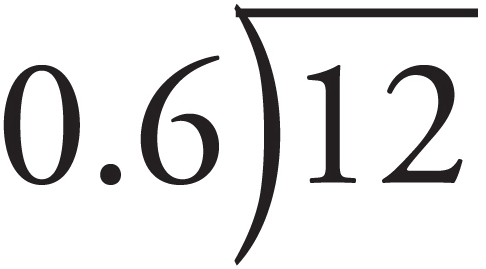
To make 0.6 (the divisor) a whole number, you simply move the decimal point over one place to the right. You must also move the decimal one place to the right in the dividend. Now the operation looks like this:
Rounding Decimals
9.4 rounded to the nearest whole number is 9.
9.5 rounded to the nearest whole number is 10.
When GMAC asks you to give an approximate answer on an easy question, it is safe to round numbers. But you should be leery about rounding numbers on a difficult question. If you’re scoring in a high percentile, rounding off numbers will be useful to eliminate answer choices that are out of the ballpark, but not to decide between two close answer choices.
DRILL 5
The answers to these questions can be found in Part VI.
On the GMAT, there might be questions that mix decimals and fractions:
5.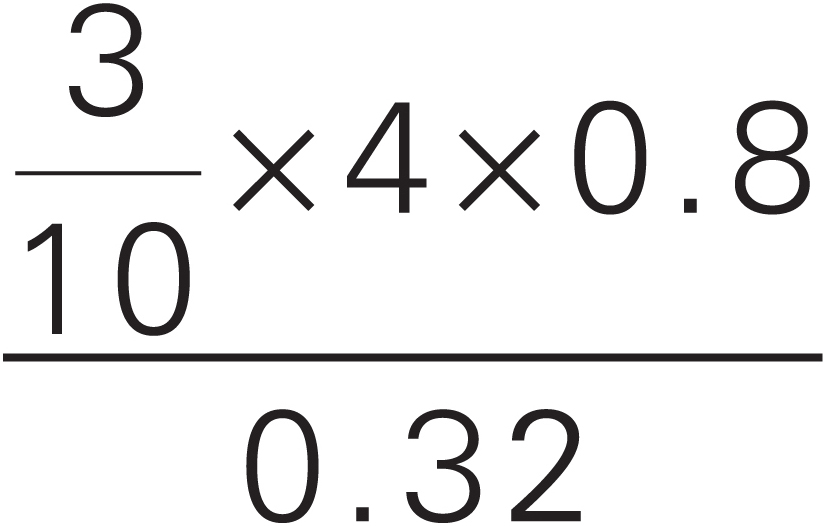
 0.96
0.96
 0.333
0.333
 3.0
3.0
 30.0
30.0
 96.0
96.0
6.If x and y are reciprocals, what is the value of x + y rounded to the nearest hundredth?
(1) x = 0.2
(2) y = 5
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are not sufficient.
Statements (1) and (2) TOGETHER are not sufficient.
RATIOS
Ratios are close relatives of fractions. A ratio can be expressed as a fraction and vice versa. The ratio 3 to 4 can be written as  as well as in standard ratio format: 3 : 4.
as well as in standard ratio format: 3 : 4.
There Is Only One Difference Between a Ratio and a Fraction
A fraction compares a part to whole relationship. A ratio compares a part to part relationship. It’s that simple. Check out the box below for a handy visual representation.
|
Fraction:
|
Ratio:
|
|
part: 3 women
|
part: 3 women
|
|
__________
|
___________
|
|
whole: 7 people
|
part: 4 men
|
(The whole is 7.)
Aside from That, All the Rules of Fractions Apply to Ratios
A ratio can be converted to a percentage or a decimal. It can be cross-multiplied, reduced, or expanded—just like a fraction. The ratio of 1 to 3 can be expressed as:
An Easy Ratio Problem
The ratio of men to women in a room is 3 to 4. If there are 20 women, what is the number of men in the room?
Here’s How to Crack It
No matter how many people are actually in the room, the ratio of men to women will always stay the same: 3 to 4. What you’re asked to do is find the numerator of a fraction whose denominator is 20, and which can be reduced to  . Just set one fraction equal to another and cross-multiply:
. Just set one fraction equal to another and cross-multiply:
The answer to the question is 15 men. Note that 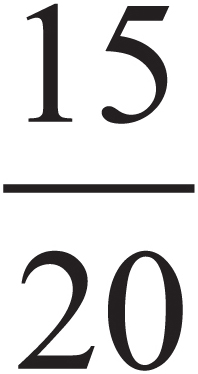 reduces to
reduces to  .
.
A More Difficult Ratio Problem
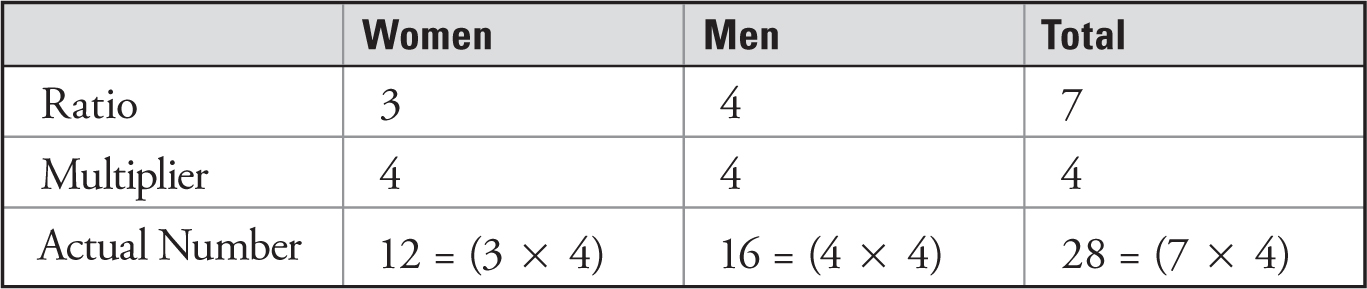
The ratio of women to men in a room is 3 to 4. If there are a total of 28 people in the room, how many are women?
This problem is more difficult because, while we are given the ratio of women to men, we are not given a specific value for either the women or the men. If we tried to set up this problem as we did the previous one, it would look like this:
Of course, you can’t solve an equation that has two variables.
Here’s How to Crack It
You need a way to see how the total number of people in the room, which you know is 28, can be broken down into groups of 3 women and 4 men.
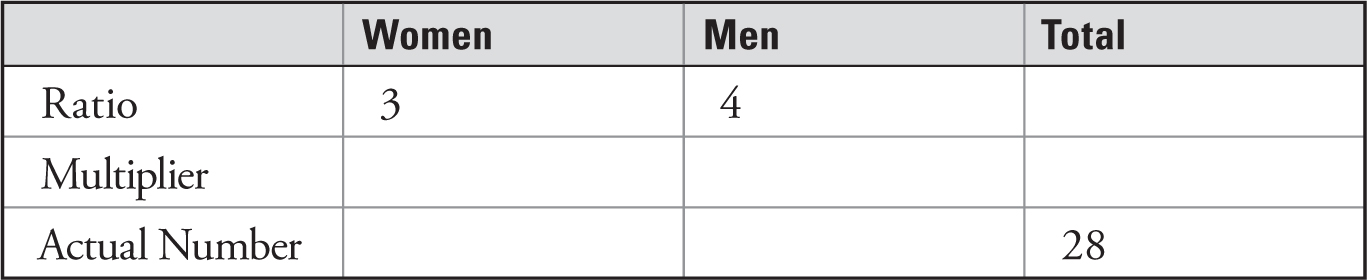
A good way to solve the problem is to use a ratio box. Here’s what that looks like for the information provided by the problem:
To use a ratio box, you need a ratio and an actual number. Now, remember that ratios compare parts to parts. So, if you add up the parts, you get a group (or total) of 7 people.
Next, the key idea of a ratio is the multiplier, which allows you to make the group greater or lesser while keeping everything in the same ratio. For this problem, you don’t want a group of 7 people. You want a group of 28. So, you multiply 7 × 4 = 28.
To keep everything in the same ratio, you just need to remember that whatever you do to one part, you need to do to every part. So, multiply the ratio numbers for both the women and men by 4.
Here’s what the box looks like when it is completed:
There are 12 women in the room.
PERCENTAGES
A percentage is just a fraction in which the denominator is always equal to 100. Fifty percent means 50 parts out of a whole of 100. Like any fraction, a percentage can be reduced, expanded, cross-multiplied, converted to a decimal, or converted to another fraction: 50% =  = 0.5.
= 0.5.
An Easy Percent Problem
5 is what percent of 20 ?
Here’s How to Crack It
Whenever you see a percent problem, you should be thinking 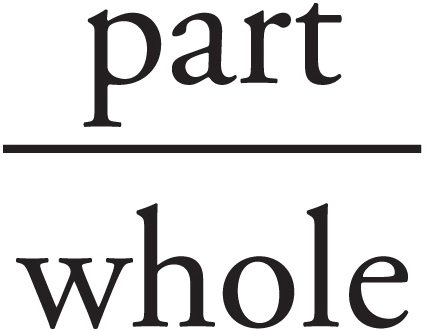 . In this case, the question asks you to expand
. In this case, the question asks you to expand 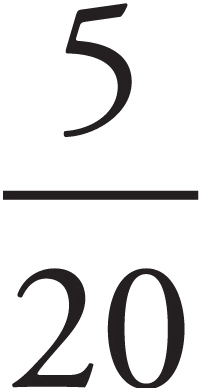 into another fraction in which the denominator is 100.
into another fraction in which the denominator is 100.
Percent Shortcuts
In the last problem, reducing 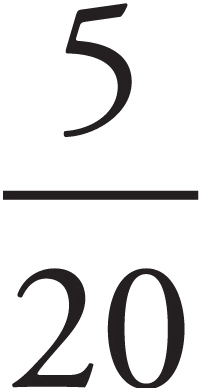 to
to  would have saved you time if you knew that
would have saved you time if you knew that  = 25%. Here are some fractions and decimals whose percent equivalents you should know:
= 25%. Here are some fractions and decimals whose percent equivalents you should know:
Some percentages simply involve moving a decimal point: To get 10 percent of any number, you simply move the decimal point of that number over one place to the left:
10% of 6 = 0.6
10% of 60 = 6
10% of 600 = 60
-
To get 1 percent of any number, you just move the decimal point of that number over two places to the left:
1% of 600 = 6
1% of 60 = 0.6
1% of 6 = 0.06
-
To find a more complicated percentage, it’s easy to break the percentage down into easy-to-find chunks:
20% of 60: 10% of 60 = 6; 20% of 60 is double 10%, so the answer is 2 × 6, or 12.
30% of 60: 10% of 60 = 6; 30% of 60 is three times 10%, so the answer is 3 × 6, or 18.
3% of 200: 1% of 200 = 2; 3% of 200 is just three times 1%, so the answer is 3 × 2, or 6.
23% of 400: 10% of 400 = 40. Therefore, 20% equals 2 × 40, or 80. 1% of 400 = 4. Therefore, 3% equals 3 × 4, or 12. Putting it all together, 23% of 400 equals 80 + 12, or 92.
A Medium Percent Problem
Like medium and difficult fraction problems, medium and difficult percent problems often involve remembering the principles of 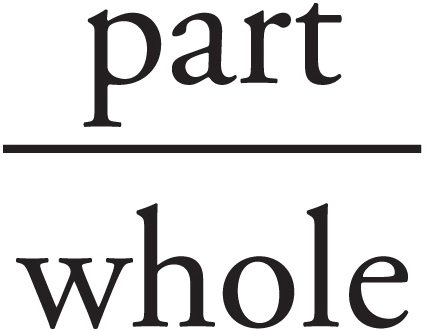 and the rest.
and the rest.
A motor pool has 300 vehicles of which 30 percent are trucks. 20 percent of all the vehicles in the motor pool are diesel, including 15 trucks. What percent of the motor pool is composed of vehicles that are neither trucks nor diesel?
 165%
165%
 90%
90%
 65%
65%
 55%
55%
 10%
10%
Here’s How to Crack It
Do this problem one sentence at a time.
-
A motor pool has 300 vehicles, of which 30% are trucks. Thirty percent of 300 = 90 trucks, which means that 210 (the rest) are not trucks.
-
Twenty percent of all the vehicles are diesel, including 15 trucks. Twenty percent of 300 = 60 diesel vehicles, 15 of which are trucks, which means there are 45 diesel vehicles that are not trucks.
-
What percent of the motor pool is composed of vehicles that are neither truck nor diesel? We know from sentence number 1 that there are 210 nontrucks. We know from sentence number 2 that of these 210 nontrucks, 45 are diesel. Therefore, 210 – 45, or 165, are neither diesel nor truck.
The question asks what percent of the entire motor pool these 165 nondiesel nontrucks are.
x = 55 and the answer is (D).
Easy Process of Elimination
-
Because the problem asks us to find a portion of the entire motor pool, it’s impossible for that portion to be greater than the motor pool itself. Therefore, (A), 165%, can be eliminated via Ballparking.
-
If the problem simply asked what percent of the motor pool was not made up of trucks, the answer would be 70%. But because there is a further condition (the vehicles must be both nontruck and nondiesel), the answer must be even less than 70%. So, (B) can be eliminated via Ballparking as well.
-
Choice (C) is a partial answer that you can get by simply adding 30 + 20 + 15, all numbers found within the problem. Choice (C) can be reasonably eliminated.
Percent Increase or Decrease
Another type of percent problem you may see on the GMAT has to do with percent increase or percent decrease. In these problems, the trick is always to put the increase or decrease in terms of the original amount. See the following example:
The cost of a one-family home was $120,000 in 1980. In 1988, the price had increased to $180,000. What was the percent increase in the cost of the home?
 60%
60%
 50%
50%
 55%
55%
 40%
40%
 33.3%
33.3%
Here’s How to Crack It
The actual increase was $60,000. To find the percent increase, set up the following equation:
In this case, 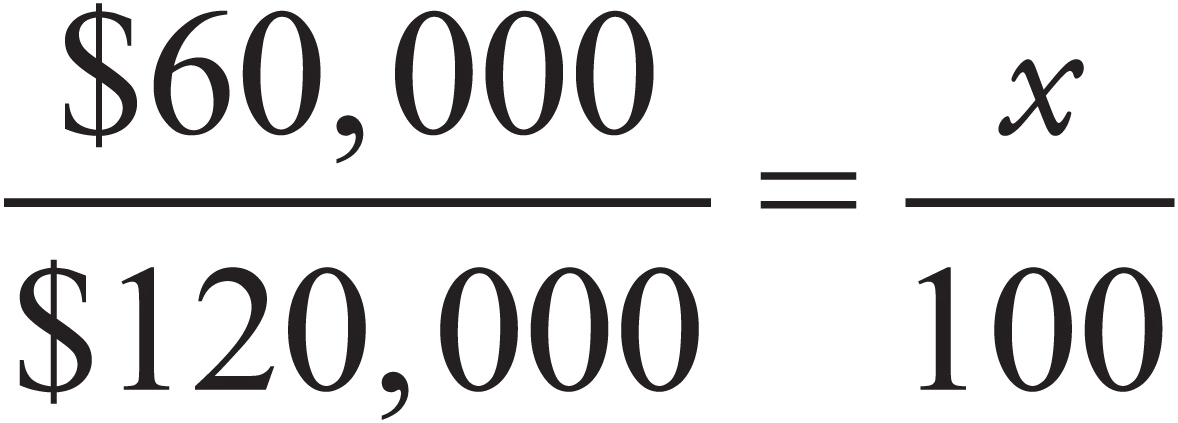 . So, x = 50 and the answer is (B).
. So, x = 50 and the answer is (B).
To solve a percent decrease problem, simply put the amount of the decrease over the original amount.
What’s the Original Amount?
GMAT test writers like to see if they can trick you into mistaking which number was the original amount. On percent decrease problems (sometimes called “percent less” problems), the original is the larger number; on percent increase problems (sometimes called “percent greater” problems), the original is the smaller number.
Compound Interest
Another type of percent problem involves compound interest. If you kept $1,000 in the bank for a year at 6% simple interest, you would get $60 in interest at the end of the year. Compound interest would pay you slightly more. Let’s look at a compound-interest problem:
Ms. Lopez deposits $100 in an account that pays 20% interest, compounded semiannually. How much money will there be in the account at the end of one year?
 $118.00
$118.00
 $120.00
$120.00
 $121.00
$121.00
 $122.00
$122.00
 $140.00
$140.00
Easy Process of Elimination
How would you work this problem if you were running out of time, or not sure how to find compound interest? Look for answer choices that can be eliminated via POE. The question asks for compound interest but (B) is the calculation of simple interest. Because finding simple interest is how to start a compound interest problem, (B) is a partial answer and can be eliminated. If you know that compound interest is always a little bit more than simple interest, you can eliminate (A) and (E) via Ballparking. Solving this problem from here requires knowledge of calculating compound interest. But, if you were having difficulty with this problem or were running out of time, POE can make this a 50-50 guess!
Here’s How to Crack It
To find compound interest, divide the interest into as many parts as are being compounded. For example, if you’re compounding interest semiannually, you divide the interest into two equal parts. If you’re compounding quarterly, you divide the interest into four equal parts.
When Ms. Lopez deposited $100 into her account at a rate of 20% compounded semiannually, the bank divided the interest into two equal parts. Halfway through the year, the bank put the first half of the interest into her account. In this case, because the full rate was 20% compounded semiannually, the bank deposited 10% of $100 (10% of $100 = $10). Halfway through the year, Ms. Lopez had $110.
For the second half of the year, the bank paid 10% interest on the $110 (10% of $110 = $11). At the end of the year, Ms. Lopez had $121.00 in her account. She earned $1 more than she would have earned if the account had paid only simple interest. The answer is (C).
AVERAGES
To find the average of a list of n numbers, you simply add the numbers and divide by n. For example:
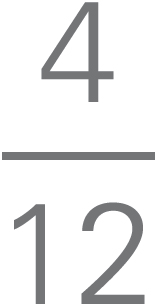
The average of 10, 3, and 5 is 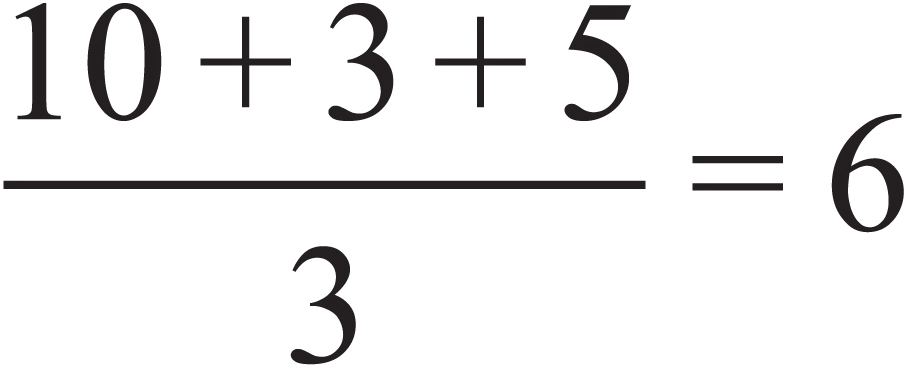 .
.
A good way to handle average problems is to set them up in the same way every time. Whenever you see the word average, you should think:
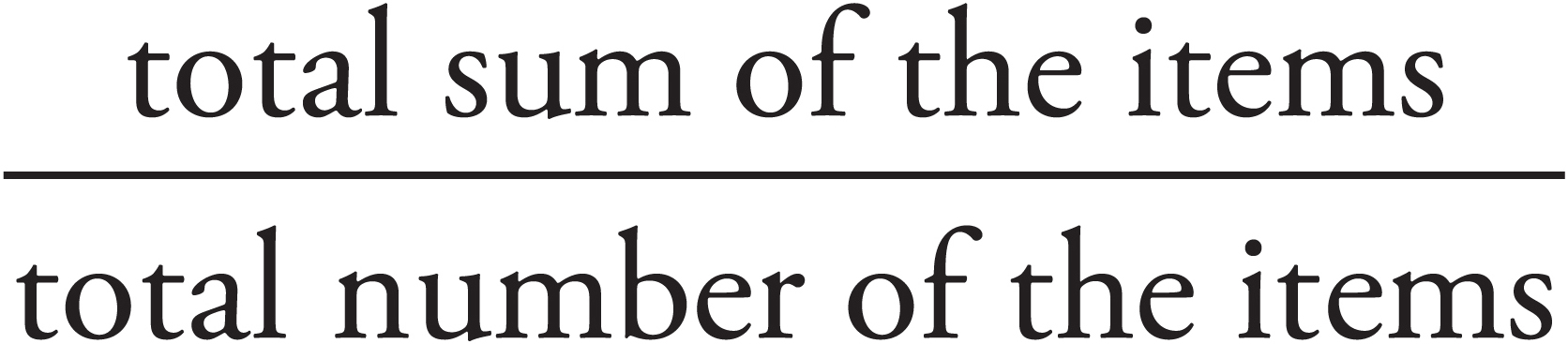 = average
= average
A One-Step Average Problem
In a simple problem, GMAC will give you two parts of this equation, and it will be up to you to figure out the third. Let’s warm up those old average skills.
What is the average (arithmetic mean) of the numbers 3, 4, 5, and 8 ?
Here’s How to Crack It
In this case they’ve given us the actual numbers, which means we know the total sum (3 + 4 + 5 + 8 = 20) and the total number of items (there are four numbers). What we’re missing is the average.
Here’s another one:
If the average (arithmetic mean) of 7 numbers is 5, what is the sum of the numbers?
Here’s How to Crack It
In this case we know the total number of items and the average, but not the total sum of the numbers.
A Two-Step Average Problem
This is the same problem you just did, made a little more difficult:
The average (arithmetic mean) of 7 numbers is 5. If two of the numbers are 11 and 14, what is the average of the remaining numbers?
The Average Test Taker
A common mistake by the average test taker is thinking you can take the average of two averages. Take a look at the following question:
If Fred’s average score on his first two tests was 70, and his average score on his next three tests was 80, what was his average score on all the tests?
The average test taker wants to say the answer is 75, which is just the average of 70 and 80. This test taker either forgets, ignores, or misses the information that the first average was based on two tests, while the second average was based on three tests. Therefore, the average test taker is not 75, and the average would get this question wrong.
Avoid this mistake by slowing down and reading the full question!
Here’s How to Crack It
Always set up an average problem the way we showed you above. With more complicated average problems, take things one sentence at a time. The first sentence yields:
The sum of all the numbers is 35. If two of those numbers are 11 and 14, then the sum of the remaining numbers is 35 – (11 + 14), or 10. The question asks, “What is the average of the remaining numbers?” Again, let’s set this up properly:
Why did we divide the total sum of the remaining numbers by 5? There were only 5 remaining numbers!
Medians and Modes
Calculating the average of a list of numbers is one way to find the “middle” of these numbers, but there are two other ways that yield slightly different results. To find the median of a list of n numbers, just reorder the numbers from least to greatest, and pick the middle number.
If n is odd, this is a piece of cake:
The median of 4, 7, 12, 14, 20 = 12.
If n is even, it’s still easy—just add the two middle numbers together and divide by 2:
The median of 4, 12, 14, 20 = 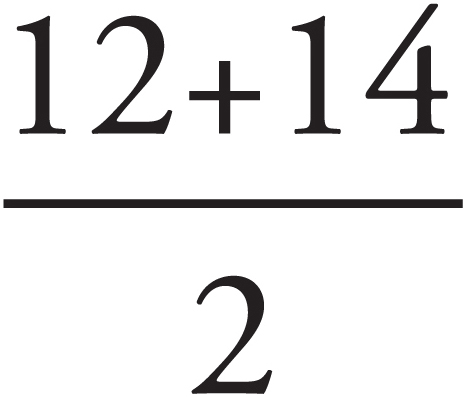 = 13.
= 13.
To find the mode of a list of n numbers, just pick the number that occurs most frequently…
The mode of 5, 6, 3, 9, 3, 28, 3, 5 = 3.
…but remember that a list of numbers can have more than one mode:
The modes of 3, 3, 3, 4, 5, 5, 5 = both 3 and 5.
Here’s a relatively easy problem:
4, 6, 3, y
If the mode of the list of numbers above is 3, then what is the average (arithmetic mean) of the list?
 7
7
 3
3
 4
4
 9
9
 12
12
Here’s How to Crack It
The mode of the list of numbers is 3, which means that y must also equal 3 (because the mode is the number that occurs most frequently in the list). So now all we have to do is find the average of 4, 6, 3, and 3. The correct answer is (C).
RANGE AND STANDARD DEVIATION
To find the range of a list of n numbers, take the least number and subtract it from the greatest number. This measures how widely the numbers are dispersed.
The range of 4, 3, 8, 12, 23, 37 = 37 – 3 = 34.
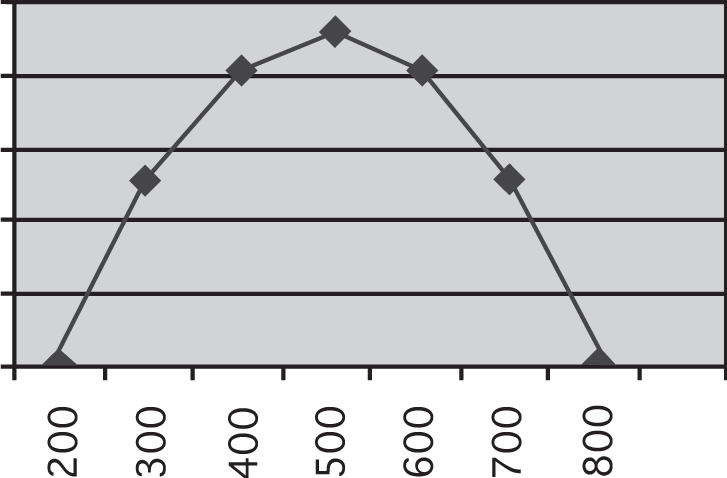
Another way to measure the dispersion of a list of numbers is standard deviation, which measures the distance between the arithmetic mean and each of the numbers in that list. Even if you think you’ve never heard of this concept before, you’ve actually seen one example of standard deviation in the form of a graph that is near and dear to the test writers’ hearts: the bell-shaped curve.
In the graph of approximate score frequencies below, you’ll notice that many people’s GMAT scores are clustered around the mean (500), with some people’s scores below and others above. The standard deviation is a number that expresses the degree to which the list of numbers vary from the mean, either above it or below it. The greater the standard deviation, the greater the degree of variation.
To calculate the standard deviation of a list of n numbers (not that the GMAT is likely to ask you to), first find the average (arithmetic mean) of the numbers. Then find the difference between that average and each number in the set and square each of the differences. And finally, find the average of the squared differences and take the square root of this average. The rather intimidating formula looks like this:
But you won’t need it.
Standard deviation usually comes down to a single number such as 2.4 or 3.0. Most GMAT questions about standard deviation concern the difference between standard deviation and the mean. Here’s a typical problem:
If the average (arithmetic mean) of a list of numbers is 12 and the standard deviation of that list of numbers is 1.3, then which of the following numbers is more than two standard deviations from the mean?
I.14.7
II.12.3
III.9.3
 I only
I only
 I and II only
I and II only
 II only
II only
 III only
III only
 I and III only
I and III only
Here’s How to Crack It
One standard deviation above the mean of 12 is 13.3, and two standard deviations is 14.6. So 14.7 (Roman numeral I) is definitely more than two standard deviations. Is the correct answer (A)? We don’t know yet—but we can definitely cross off (C) and (D) because they don’t include Roman Numeral I. Let’s look at Roman Numeral II. 12.3 is definitely less than two standard deviations, so we can cross off (B). Now, you may have wanted to cross off (E) as well, because 9.3 (Roman Numeral III) is much less than 14.6—but remember, standard deviation means a deviation either above or below the mean. Two standard deviations below 12 is 9.4, so 9.3 is actually more than two standard deviations from the mean. The correct answer is (E).
EXPONENTS
An exponent is a short way of writing the value of a number multiplied several times by itself. 4 × 4 × 4 × 4 × 4 can also be written as 45. This is expressed as “four to the fifth power.” The large number (4) is called the base, and the little number (5) is called the exponent.
There are several rules to remember about exponents:
-
Multiplying numbers with the same base: When you multiply numbers that have the same base, you simply add their exponents.
62 × 63 = 6(2 + 3) = 65(y4)(y6) = y(4 + 6) = y10
-
Dividing numbers with the same base: When you divide numbers that have the same base, you simply subtract the bottom exponents from the top exponents.
-
Raising a power to a power: When you raise a number with an exponent to another power, you can simply multiply the exponents.
(43)2 = 4(3 × 2) = 46(z2)4 = z(2 × 4) = z8
There are several operations that seem like they ought to work with exponents, but don’t.
| • |
Does x2 + x3 = x5 ?
|
NO! |
| • |
Does x6 – x2 = x4 ?
|
NO! |
| • |
Does 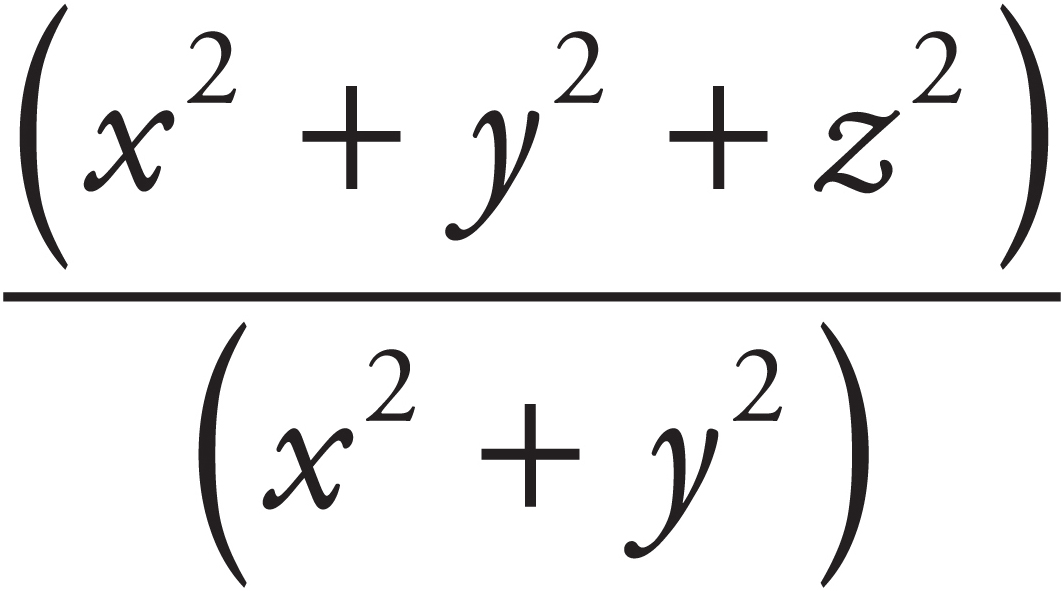 = z2 ? = z2 ?
|
NO! |
But note that in the first example, x2 + x3 can be written in another form, using the distributive property: x2 + x3= x2(1 + x).
The Strange Powers of Powers
If you raise a positive integer to a power, the result is greater than the original integer. For example, 62 = 36. However, raising a number to a power can sometimes have unexpected results:
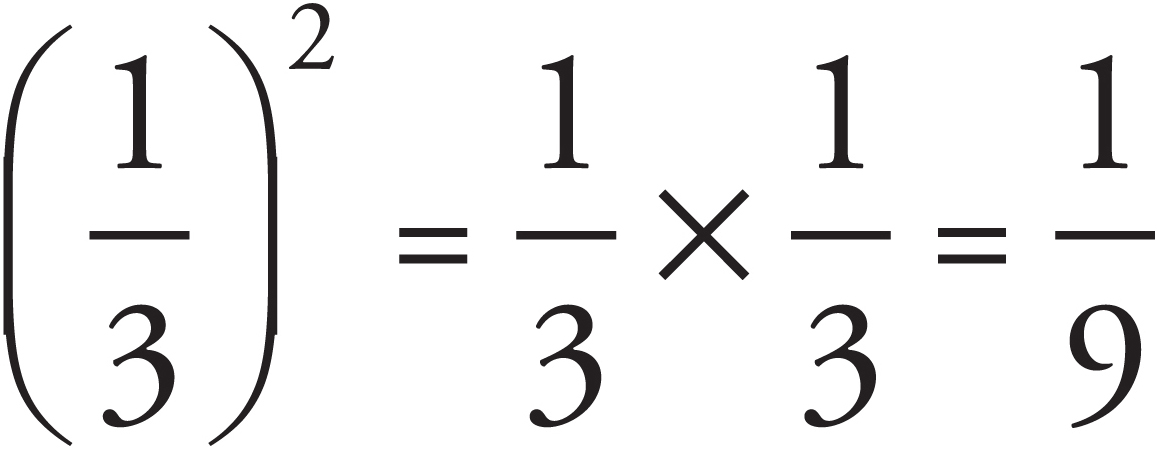
-
If you raise a negative number to an odd power, the result is less than the original number.
(–3)3 = (–3)(–3)(–3) = –27
(Remember, –27 is smaller than –3.)
-
If you raise a negative number to an even power, the result is positive.
(–3)2 = (–3)(–3) = 9
(Remember, negative times negative = positive.)
-
Any number to the first power = itself.
-
Any nonzero number raised to the 0 power = 1.
RADICALS
The square root of a positive number x is the number that, when squared, equals x. By definition, you can take the square root of only a nonnegative number and the square root function returns only nonnegative values. The symbol for a square root is 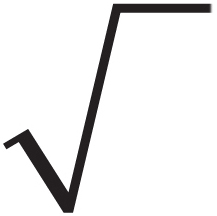 . A number inside the
. A number inside the 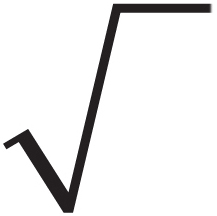 is called a radical. Thus, in
is called a radical. Thus, in 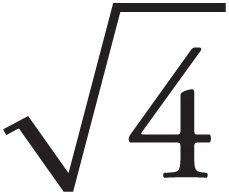 = 2, 4 is the radical and 2 is its square root.
= 2, 4 is the radical and 2 is its square root.
The cube root of a positive number x is the number that, when cubed, equals x. For example, the cube root of 8 is 2, because 2 × 2 × 2 = 8. The symbol for a cube root is  . Thus, the cube root of 27 would be represented as
. Thus, the cube root of 27 would be represented as  = 3, because 3 × 3 × 3 = 27. The cube root of –27 would be represented as
= 3, because 3 × 3 × 3 = 27. The cube root of –27 would be represented as 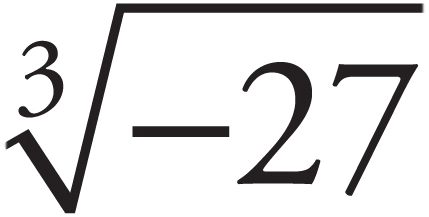 = –3 because –3 × –3 × –3 = –27.
= –3 because –3 × –3 × –3 = –27.
There are several rules to remember about radicals:
-
 =
=  . For example,
. For example, 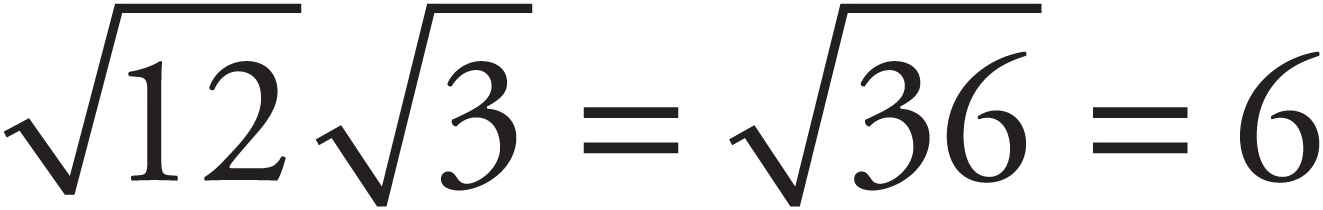 .
.
-
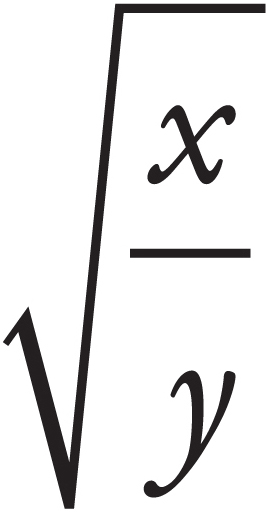 =
= 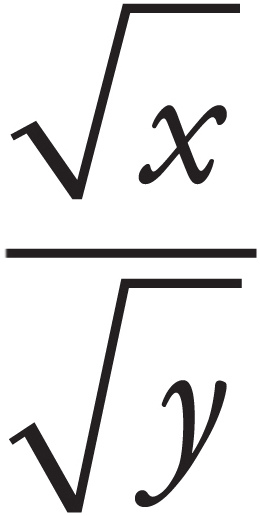 . For example,
. For example,  .
.
-
To simplify a radical, try factoring. For example,  .
.
-
The square root of a positive fraction less than 1 is actually larger than the original fraction. For example,  .
.
DRILL 6
The answers to these questions can be found in Part VI.
1. If 2 men and 1 woman drop out of a certain class, the ratio of men to women in the class would be 8 to 7. If the current ratio of men to women in the class is 6 to 5, then how many men are currently in the class?
 14
14
 16
16
 18
18
 20
20
 22
22
2. The average (arithmetic mean) of five numbers is 7. If the average of three of the numbers is 5, then what is the average of the other two numbers?
 5
5
 10
10
 12
12
 15
15
 20
20
3. 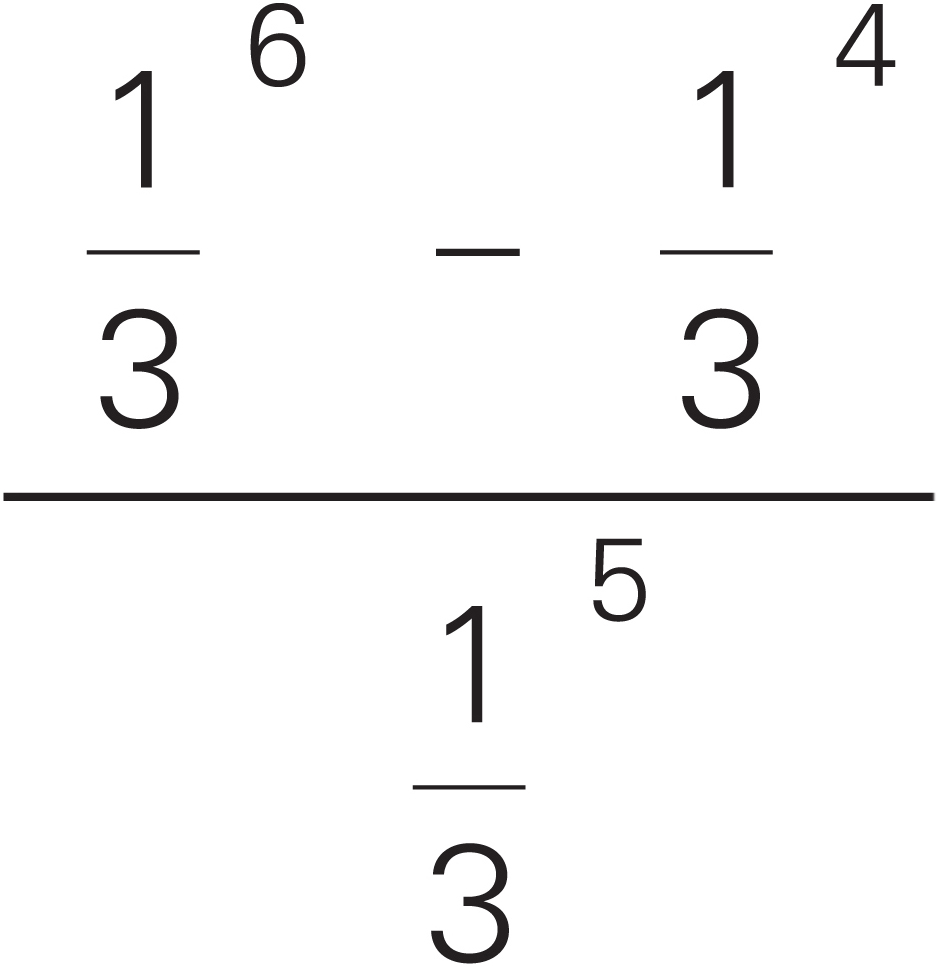 =
=

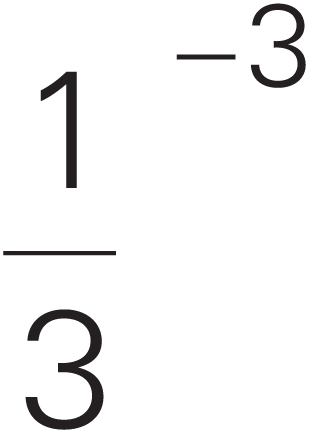

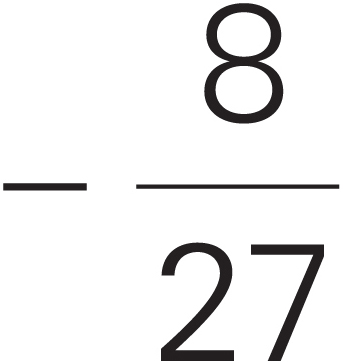

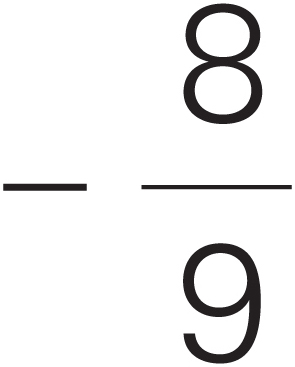

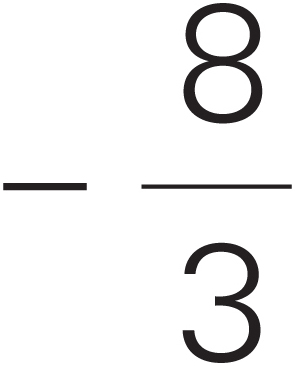

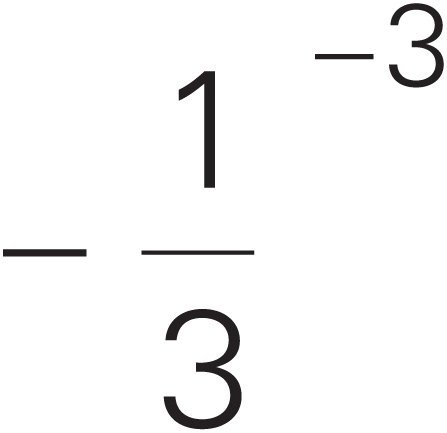
4. The ratio 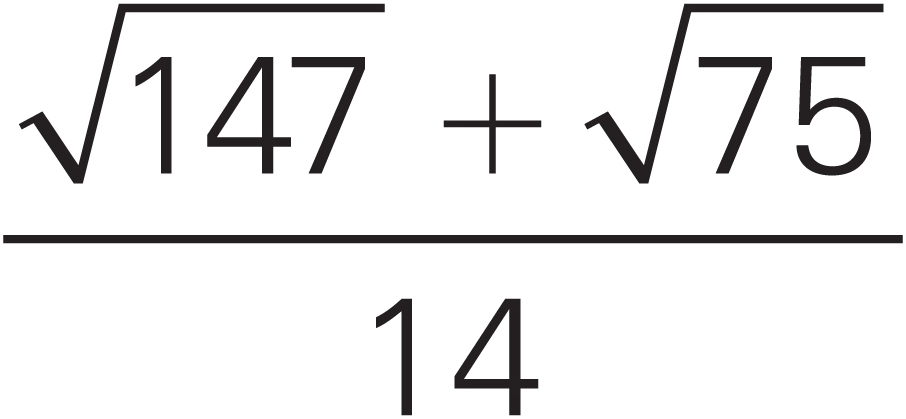 to
to 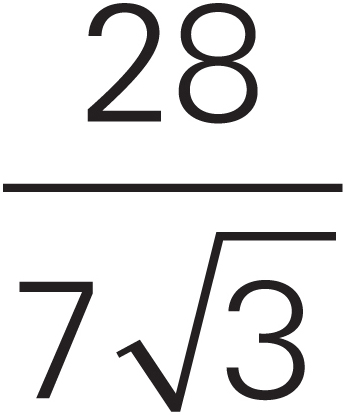 is equal to
is equal to

 to 2
to 2
 24 to 7
24 to 7
 14 to 9
14 to 9
 9 to 14
9 to 14
 7 to 24
7 to 24
5. If $5,000 is invested in an account that earns 8% interest compounded semi-annually, then the interest earned after one year would be how much greater than if the $5,000 had been invested at 8% simple yearly interest?
 $4
$4
 $8
$8
 $12
$12
 $16
$16
 $432
$432
6. If the average of ten numbers is 10, then which of the following could be the standard deviation of the ten numbers?
I. 0
II. 10
III. 20
 I only
I only
 I and II
I and II
 I and III
I and III
 II and III
II and III
 I, II, and III
I, II, and III
7. List I: {y, 2, 4, 7, 10, 11}
List II: {3, 3, 4, 6, 7, 10}
If the median of List I is equal to the sum of the median of list II and the mode of List II, then y equals
 5
5
 7
7
 8
8
 9
9
 10
10
A bar over a digit in a decimal indicates an infinitely repeating decimal.
333,333.3 × (10–3 – 10–5) =
 3,333.3
3,333.3
 3,330
3,330
 333.3
333.3
 330
330
 0
0
Summary
-
The six arithmetic operations are addition, subtraction, multiplication, division, raising to a power, and finding a square root.
-
These operations must be performed in the proper order (Please Excuse My Dear Aunt Sally).
-
If you are adding or multiplying a group of numbers, you can regroup them in any order. This is called the associative law.
-
If you are adding or subtracting numbers with common factors, you can regroup them in the following way:
ab + ac = a(b + c)
ab – ac = a(b – c)
This is called the distributive law.
-
A fraction can be thought of in two ways:
-
You must know how to add, subtract, multiply, and divide fractions. You must also know how to raise them to a power and find their roots.
-
Always reduce fractions (when you can) before doing a complicated operation. This will reduce your chances of making a careless error.
-
In tough fraction problems, always think 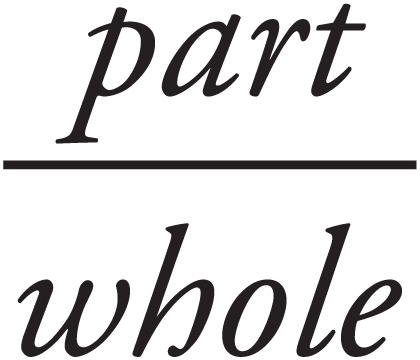 and the rest.
and the rest.
-
A decimal is just another way of expressing a fraction.
-
You must know how to add, subtract, multiply, and divide decimals.
-
In general it is easier to work with fractions than with decimals, so convert decimals to fractions.
-
A ratio is a fraction in all ways but one:
-
A percentage is just a fraction whose denominator is always 100.
-
You must know the percentage shortcuts outlined in this chapter.
-
In tough percent problems, like tough fraction problems, think 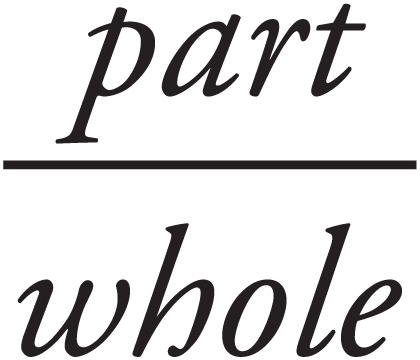 and the rest.
and the rest.
-
In a percentage increase or decrease problem, you must put the amount of the increase or decrease over the original amount.
-
In compound interest problems, the answer will always be a little bit more than it would be in a similar simple interest problem.
-
To find the average of several values, add the values and divide the total by the number of values.
-
Always set up average problems in the same way:
-
To find the median of a list of n numbers, reorder the numbers from least to greatest, and pick the middle number if n is odd. Take the average of the two middle numbers if n is even.
-
To find the mode of a list of n numbers, pick the number that occurs most frequently.
-
To find the range of a list of n numbers, subtract the smallest number from the greatest number.
-
Standard deviation measures the distance between a set of numbers and its arithmetic mean. Most GMAT problems about this concept hinge on the difference between the standard deviation and the arithmetic mean.
-
An exponent is a shorter way of expressing the result of multiplying a number several times by itself.
-
When you multiply numbers with the same base, you simply add the exponents.
-
When you divide numbers with the same base, you simply subtract the exponents.
-
When you raise a power to a power, you multiply the exponents.
-
You cannot add or subtract numbers with the same or different bases by adding their exponents.
-
The three radical rules you need to know:
-
There are some unusual features of exponents and radicals:
-
The square root of a positive fraction that’s less than 1 is larger than the original fraction.
-
When you raise a positive fraction that’s less than 1 to an exponent, the resulting fraction is smaller.
-
When you raise a negative number to an even exponent, the resulting number is positive.
-
When you raise a negative number to an odd exponent, the resulting number is still a negative number.
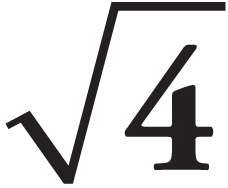 )
)