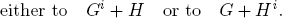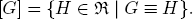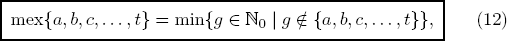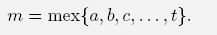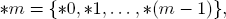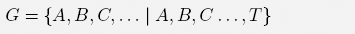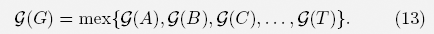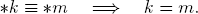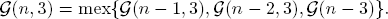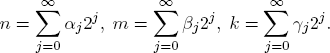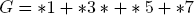Chapter 2
Combinatorial Games
Games can always be understood as to involve two players that execute moves alternatingly. This aspect reveals a recursive character of games. The chapter takes a look at games that are guaranteed to end after a finite number of moves. Finite games are said to be combinatorial. Under the normal winning rule, combinatorial games have an algebraic structure and behave like generalized numbers. Game algebra allows one to explicitly compute winning strategies for nim games, for example.
1.Alternating players
Let Γ be a game that is played on a system 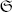 and recall that Γ represents the collection of all possible stages in an abstract sense. Assume that a concrete instance of Γ starts with the initial state σ0 ∈
and recall that Γ represents the collection of all possible stages in an abstract sense. Assume that a concrete instance of Γ starts with the initial state σ0 ∈ 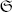 . Then we may imagine that the evolution of the game is caused by two “superplayers” that alternate with the following moves:
. Then we may imagine that the evolution of the game is caused by two “superplayers” that alternate with the following moves:
(1)The beginning player chooses a stage γ1 = σ0σ1 ∈ Γ.
(2)The second player extends γ1 to a stage γ2 = σ0σ1σ2 ∈ Γ.
(3)Now it is again the turn of the first player to realize the next feasible stage γ3 = σ0σ2σ3 ∈ Γ and so on.
(4)The game stops if the player which would be next to move cannot find a feasible extension γt+1 ∈ Γ of the current stage γt.
This point of view allows us to interpret the evolution of a game as the evolution of a so-called alternating 2-person game. For such a game  , we assume
, we assume
| (A0) |
There is a set  and two players L and R and an initial element G0 ∈ and two players L and R and an initial element G0 ∈  . . |
| (A1) |
For every G ∈  , there are subsets GL ⊆ , there are subsets GL ⊆  and GR ⊆ and GR ⊆  . . |
The two sets GL and GR in (A1) are the sets of options of the respective players relative to G.
The rules of the alternating game  are:
are:
| (A3) |
The beginning player chooses an option G1 relative to G0. Then the second player chooses an option G2 relative to G1. Now the first player may select an option G3 relative to G2 and so on. |
| (A4) |
The game stops with Gt if the player whose turn it is has no option relative to Gt (i.e., the corresponding option set is empty). |
EX. 2.1 (Chess). Chess is an obvious example of an alternating 2-person game. Its stopping rule (A4) says that the game ends when a player’s king has been taken (“checkmate”).
REMARK 2.1. While a chess game always starts with a move of the white player, notice that we have not specified whether L or R is the first player in the general definition of an altenating 2-person game. This lack of specification will offer the necessary flexibility in the recursive analysis of games below.
2.Recursiveness
An alternating 2-person game  as above has a recursive structure:
as above has a recursive structure:
| (R) |
A feasible move G → G′ of a player reduces the current game to a new alternating 2-player game with initial element G′. |
To make this conceptually clear, we denote the options of the players L (“left”) and R (“right”) relative to G as

and think of G as the (recursive) description of a game that could possibly be reduced by L to a game 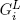 or by R to a game
or by R to a game 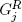 , depending on whose turn it is to make a move.
, depending on whose turn it is to make a move.
3.Combinatorial games
Consider an alternating 2-person game in its recursive form (11):

Denoting by |G| the maximal number of subsequent moves that are possible in G, we say that G is a combinatorial game if

i.e., if G is guaranteed to stop after a finite number of moves (no matter which player starts). Clearly, all the options 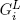 and
and 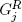 of G must then be combinatorial games as well:
of G must then be combinatorial games as well:

EX. 2.2 (Chess). According to its standard rules, chess is not a combinatorial game because the players could move pieces back and forth and thus create a never ending sequence of moves. In practice, chess is played with an additional rule that ensures finiteness and thus makes it combinatorial (in the sense above). The use of a timing clock, for example, limits the the number of moves.
EX. 2.3 (Nim). The nim game G = G(N1, . . . , Nk) has two alternating players and starts with the initial configuration of a collection of k finite and pairwise disjoint sets N1, . . . , Nk. A move of a player is:
•Select one of these sets, say Nj, and remove one or more of the elements from Nj.
Clearly, one has

So nim is a combinatorial game.a
_____________________________
aA popular version of nim starts from four sets N1, N2, N3, N4 of pieces (pebbles or matches, etc.) with |N1| = 1, |N2| = 3, |N3| = 5 and |N4| = 7 elements.
EX. 2.4 (Frogs). Having fixed numbers n and k, two frogs L and R sit n positions apart. A move of a frog consists in taking a leap of at least 1 but not more than k positions toward the other frog:

The frogs are not allowed to jump over each other. Obviously, the game ends after at most n moves.
REMARK 2.2. The game of frogs in Ex. 2.4 can be understood as a nim game with an additional move restriction. Initially, there is a set N with n elements (which correspond to the positions separating the frogs). A player must remove at least 1 but not more than k elements.
Creation of combinatorial games. The class  of all combinatorial games can be created systematically. We first observe that there is exactly one combinatorial game G with |G| = 0, namely the game
of all combinatorial games can be created systematically. We first observe that there is exactly one combinatorial game G with |G| = 0, namely the game

in which no player has an option to move. Recall furthermore that all options GL and GR of a game G with |G| = t must satisfy |GL| ≤ t−1 and |GR| ≤ t − 1. So we can imagine that  is “created” in a never ending process from day to day:
is “created” in a never ending process from day to day:
DAY 0: The game O = {· | ·} is created and yields  0 = {O}.
0 = {O}.
DAY 1: The games {O|·}, {· | O}, {O | O} are created and one obtains the class

of all combinatorial games G with |G| ≤ 1.
DAY 2: The creation of the class  2 of those combinatorial games with options in
2 of those combinatorial games with options in  1 is completed. These include the games already in
1 is completed. These include the games already in  1 and the new games
1 and the new games

DAY t: The class  t of all those combinatorial games G with options in
t of all those combinatorial games G with options in  t−1 is created.
t−1 is created.
So one has  0 ⊂
0 ⊂  1 ⊂ . . . ⊂
1 ⊂ . . . ⊂  t ⊂ . . . and
t ⊂ . . . and

EX. 2.5. The number of combinatorial games grows rapidly:
(1)List all the combinatorial games in  2.
2.
(2)Argue that many more than 6000 combinatorial games exist at the end of DAY 3 (see Ex. 2.6).
EX. 2.6. Show that rt = | t| grows super-exponentially fast:
t| grows super-exponentially fast:

(Hint: A finite set S with n = |S| elements admits 2n subsets.)
4.Winning strategies
A combinatorial game is started with either L or R making the first move. This determines the first player. The other player is the second player. The normal winning rule for an alternating 2-person games is:
| (NR) |
If a player i ∈ {L, R} cannot move, player i has lost and the other player is declared the winner. |
Chess matches, for example, are played under the normal rule: A loss of the king means a loss of the match (see Ex. 2.1).
REMARK 2.3 (Misère). The misère rule declares the player with no move to be the winner of the game.
A winning strategy for player i is a move (option) selection rule for i that ensures i to end as the winner.
THEOREM 2.1. In any combinatorial game G, an overall winning strategy exists for either the first or the second player.
Proof. We prove the theorem by mathematical induction on t = |G|. In the case t = 0, we have

Because the first player has no move in O, the second player is automatically the winner in normal play and hence has a winning strategy trivially guaranteed. Under the misère rule, the first player wins.
Suppose now t ≥ 1 and that the theorem is true for all games that were created on DAY t − 1 or before. Consider the first player in G and assume that it is R. (The argument for L would go exactly the same way!)
If R has no option, L is the declared winner in normal play while R is the declared the winner in misère play. Either way, G has a guaranteed winner.
If options GR exist, the induction hypothesis says that each of R’s options leads to a situation in which either the first or the second player would have a winning strategy.
If there is (at least) one option GR with the second player as the winner, R can take this option and win as the second player in GR.
On the other hand, if all of R’s options have their first player as the winner, there is nothing R can do to prevent L from winning. So the originally second player L has a guaranteed overall strategy to win the game.

Note that the proof of Theorem 2.1 is constructive in the following sense:
(1)Player i marks by υ(Gi) = +1 all the options Gi in G that would have i winning as the then second player and sets υ(Gi) = −1 otherwise.
(2)Player i follows the strategy to move to an option with the highest υ-value.
(3)Provided a winning strategy exists at all for i, strategy (2) is a winning strategy for i.
The reader must be cautioned, however. The concrete computation of a winning strategy may be a very difficult task in real life.
EX. 2.7 (DE BRUIJN’s game). Two players choose a natural number n ≥ 1 and write down all n numbers

A move of a player consists in selecting one of the numbers still present and erasing it together with all its (proper or improper) divisors.
Note that a winning strategy exists for the first player in normal play. Indeed, if it existed for the second player, the first player could simply erase “1” on the first move and afterwards (being now the second player) follow that strategy and win. Alas, no practically efficient method for the computation of a winning strategy is known.
REMARK 2.4. If chess is played with a finiteness rule, then a winning strategy exists for one of the two players. Currently, however, it is not known what it looks like. It is not even known which player is the potentially guaranteed winner.
Playing in practice. While winning strategies can be computed in principle (see the proof of Theorem 2.1), the combinatorial structure of many games is so complex that even today’s computers cannot perform the computation efficiently.
In practice, a player i will proceed according to the following υ-greedy strategy1:
| (υgi) |
Assign a quality estimate υ(Gi) ∈ ℝ to all the options Gi and move to an option with a highest υ-value. |
A quality estimate υ is not necessarily completely pre-defined by the game in absolute terms but may reflect previous experience and other considerations. Once quality measures are accepted as “reasonable”, it is perhaps natural to expect that the game would evolve according to greedy strategies relative to these measures.
EX. 2.8. A popular rule of thumb evaluates the quality of a chess configuration σ for a player W, say, by assigning a numerical weight υ to the white pieces on the board. For example:

Where υ(σ) is the total weight of the white pieces, a υ-greedy player W would choose a move to a configuration σ with a maximal value υ(σ). (Player B can, of course, evaluate the black pieces similarly.)
5.Algebra of games
For the rest of the chapter we will (unless explicitly said otherwise) assume:
•The combinatorial games under consideration are played with the normal winning rule.
The set  of combinatorial games carries an algebraic structure which allows us to do computations with games as generalized numbers. This section wants to give a short sketch of the idea.2
of combinatorial games carries an algebraic structure which allows us to do computations with games as generalized numbers. This section wants to give a short sketch of the idea.2
Negation. We first define the negation (–G) for the game

as the game that arises from G when the players L and R interchange their roles: L becomes the “right” and R the “left” player.
So we obtain the negated games recursively as

Also –G is a combinatorial game and one has the straightforward algebraic rule

Addition. The sum G + H of the games G and H is the game in which a player i ∈ {L, R} may choose to play either on G or on H. This means that i chooses an option Gi in G or an option Hi in H and accordingly reduces the game
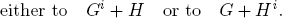
The reader is invited to verify the further algebraic rules:

Moreover, we write

EX. 2.9. The second player wins G − G (= G + (−G)) in normal play with the obvious strategy:
•Imitate every move of the first player:
When the first player chooses the option Gi in G, the second player will answer with the option (−Gi) in (−G), etc.
5.1.Congruent games
Motivated by Ex. 2.9, we say that combinatorial games G and H are congruent (notation: “G ≡ H”) if
| (C) |
G − H can be won by the second player (in normal play). |
In particular, G ≡ O means that the second player has a winning strategy for G.
THEOREM 2.2 (Congruence Theorem). For all G, H, K ∈  , one has:
, one has:
| (a) |
If G ≡ H, then H ≡ G. |
| (b) |
If G ≡ H, then G + K ≡ H + K. |
| (c) |
If G ≡ H and H ≡ K, then G ≡ K. |
Proof. The verification of the commutativity rule (a) is left to the reader. To see that (b) is true, we consider the game

The game K − K can always be won by the second player (Ex. 2.9). Hence, if the second player can win G − H, then clearly M as well:
•It suffices for the second player to apply the respective winning strategies to G – H and to K – K.
The proof of the transitivity rule (c) is similar. By assumption, the game

can be won by the second player. We must show that the second player can therefore win G – K.
Suppose to the contrary that G – K ≢ O were true and that the game G – K could be won by the first player. Then the first player could win T by beginning with a winning move in G – K and continuing with the win strategy whenever the second player moves in G – K. If the second player moves in K – K, the first player becomes second there and thus is assured to win on K – K! So the first player would win T, which would contradict the assumption however.
Hence we conclude that G – K ≡ O must hold.

Congruence classes. For any G ∈  , the class of congruent games is
, the class of congruent games is
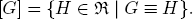
Theorem 2.2 says that addition and subtraction can be meaningfully defined for congruence classes:

In particular, we obtain the familiar algebraic rule

where [O] is the class of all combinatorial games that are won by the second player. Hence we can re-cast the optimal strategy for a player (under the normality rule):
•Winning strategy:
Make a move G → G′ to an option G′ ∈ [O].
5.2.Strategic equivalence
Say that the combinatorial games G and H are strategically equivalent (denoted “G ~ H”) if one of the following statements is true:
| (SE1) |
G and H can be won by the first player (i.e., G ≢ O ≢ H). |
| (SE2) |
G and H can be won by the second player (i.e., G ≡ O ≡ H). |
THEOREM 2.3 (Strategic equivalence). Congruent games G, H ∈  are strategically equivalent, i.e.,
are strategically equivalent, i.e.,

Proof. We claim that strategically non-equivalent games G and H cannot be congruent.
So assume, for example, that the first player wins G (i.e., G ≢ O), and the second player wins H (i.e., H ≡ O and hence (−H) ≡ O). We will argue that the first player has a winning strategy for G − H, which means G ≢ H.
Indeed, the first player can begin with a winning strategy on G. Once the second player moves on (−H), the first player, being now the second player on (−H), wins there. Thus an overall victory is guaranteed for the first player.

6.Impartial games
A combinatorial game G is said to be impartial (or neutral) if both players have the same options. The formal definition is recursive:
•O = {· | ·} is impartial.
•G = {A, B, . . . , T | A, B, . . . } is impartial if all the options A, B, . . . , T are impartial.
Notice the following rules for impartial games G and H:
(1)G = −G and hence G + G = G – G ∈ [O].
(2)G + H is impartial.
EX. 2.10. Show that the frog game of Ex. 2.4 is impartial.
Nim is the prototypical impartial game (as the SPRAGUE–GRUNDY Theorem 2.4 will show below).
To formalize this claim, we use the notation *n for a nim game relative to just one single set N1 with n = |N1| elements. The options of *n are the nim games

Moreover,

is the nim game described in Ex. 2.3 with k piles of sizes n1, n2 , . . . , nk.
We now define the mex3 of numbers a, b, c . . . , t as the smallest natural number g that equals none of the numbers a, b, c, . . . , t:
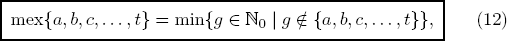
The crucial observation is stated in Lemma 2.1.
LEMMA 2.1. For any finitely many numbers a, b, c, . . . , t ∈ ℕ0, one has

i.e., the impartial game G with the nim options *a, *b, *c, . . . , *t is congruent with the simple nim game *m with
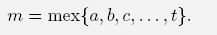
Proof. In view of *m = –*m, we must show: G + *m ≡ O, i.e., the second player wins G + *m. Indeed, if the first player chooses an option *j from
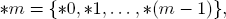
then the second player can choose *j from G (which must exist because of the definition of m as the minimal excluded number) and continue to win *j + *j as the second player.
If the first player selects an option from G, say *a, we distinguish two cases. If a > m then the second player reduces *a to *m and wins. If a < m, then the second player can reduce *m to *a and win. (Note that a = m is impossible by the definition of mex.)

THEOREM 2.4 (SPRAGUE–GRUNDY). Every impartial combinatorial game
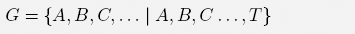
is congruent to a unique nim game of type *m. m is the so-called GRUNDY number of G and denoted by  (G).
(G).
 (G) of can be computed recursively from the GRUNDY numbers of the options:
(G) of can be computed recursively from the GRUNDY numbers of the options:
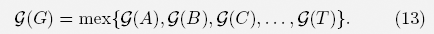
Proof. We prove the theorem by induction on |G| and note G ≡ O if |G| = 0. By induction, we now assume that the theorem is true for all options of G, i.e., A ≡ *a, B ≡ *b etc. with a =  (A), b =
(A), b =  (B), etc.
(B), etc.
Hence we can argue G ≡ *m = * (G) exactly as in the proof of Lemma 2.1. G cannot be congruent with another nim game *k since (as Ex. 2.11 below shows):
(G) exactly as in the proof of Lemma 2.1. G cannot be congruent with another nim game *k since (as Ex. 2.11 below shows):
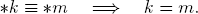

EX. 2.11. Show for all natural numbers k and n:

EX. 2.12 (GRUNDY number of frogs). Let F(n, k) be the (impartial) frog game of Ex. 2.4 and  (n, k) its GRUNDY number. For k = 3, F(n, k) has the options
(n, k) its GRUNDY number. For k = 3, F(n, k) has the options

So the associated GRUNDY number  (n, 3) has the recursion
(n, 3) has the recursion
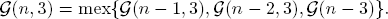
Clearly,  (0, 3) = 0,
(0, 3) = 0,  (1, 3) = 1 and
(1, 3) = 1 and  (2, 3) = 2. The recursion then produces the subsequent GRUNDY numbers:
(2, 3) = 2. The recursion then produces the subsequent GRUNDY numbers:

The second player wins the nim game *m if and only if m = 0. So the first player can win exactly the impartial games G with GRUNDY number  (G) ≠ 0. In general, we note:
(G) ≠ 0. In general, we note:
•Winning strategy for impartial games:
Make a move G → G′ to an option G′ with a GRUNDY number  (G′) = 0.
(G′) = 0.
6.1.Sums of GRUNDY numbers
If G and H are impartial games with GRUNDY numbers m =  (G) and n =
(G) and n =  (H), the GRUNDY number of their sum is
(H), the GRUNDY number of their sum is

Indeed, if G ≡ *m and H ≡ *n, then G + H ≡ *m + *n must hold.4 For the study of sums, we may therefore restrict ourselves to nim games. Moreover, the fundamental property

suggests to study sums in the context of binary algebra.
Binary algebra. Recall that every natural number n has a unique binary representation in terms of powers of 2,

with binary coefficients αj ∈ {0, 1}. We define binary addition of 0 and 1 (as in Section 1.2.3) according to the rules

and extend it to natural numbers:

REMARK 2.5. Notice that the binary representation of a natural number has only finitely many non-zero summands. Indeed, αj = 0 must hold for all j > log2 n if

EX. 2.13. Show for the binary addition of natural numbers m, n, k:

The sum theorem. We consider nim games with three piles of n, m and k objects, i.e., sums of three single nim games *n, *m, and *k.
LEMMA 2.2. For all numbers n, m, k ∈ ℕ0, one has:
(1)If n⊕m⊕k ≠ 0, then the first player wins *n + *m + *k.
(2)If n⊕m⊕k = 0, then the second player wins *n+*m+*k.
Proof. We prove the lemma by induction on n + m + k and note that the statements (1) and (2) are obviously true in the case

By induction, we now assume that the lemma is true for all n′, m′, k′ ∈ ℕ0 such that

We must then show that the lemma holds for n, m, k with the binary representations
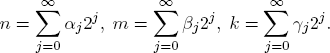
In the case (1) with n ⊕ m ⊕ k ≠ 0, there must be at least one j such that

Let J be the largest such index j. Two of these coefficients αJ, βJ, γJ must be equal and the third one must have value 1. So suppose αJ = βJ and γJ = 1, for example, which implies

Let k′ = n ⊕ m. We claim that the first player can win by reducing *k to *k′. Indeed, the induction hypothesis says that the lemma is true for n, m, k′. Since

property (2) guarantees a winning strategy for the second player in the reduced nim game

But the latter is the originally first player! So statement (1) is found to be true.
In case (2), when n ⊕ m ⊕ k = 0, the first player must make a move on one of the three piles. Let us say that *n is reduced to *n′. Because n = m ⊕ k, we have

Because the lemma is assumed to be true for n′, m, k, statement (1) guarantees a winning strategy for the first player in the reduced game

which is the originally second player.

THEOREM 2.5 (Sums of impartial games). For any impartial combinatorial games G and H, one has

Proof. Let n =  (G) and m =
(G) and m =  (H) and k = n ⊕ m. Then n ⊕ m + k = 0 holds. So Lemma 2.2 says that the second player wins
(H) and k = n ⊕ m. Then n ⊕ m + k = 0 holds. So Lemma 2.2 says that the second player wins

which yields

Consequently, n ⊕ m must be the GRUNDY number of G + H.

We illustrate Theorem 2.5 with the nim game
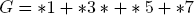
of four piles with 1,3,5 and 7 objects respectively. The binary representations of the pile sizes are

So the GRUNDY number of G is

Hence G can be won by the second player in normal play.
EX. 2.14. Suppose that the first player removes 3 objects from the pile of size 7 in G = *1 + *3 * + *5 + *7. How should the second player respond?
EX. 2.15. There is a pile of 10 red and another pile of 10 black pebbles. Two players move alternatingly with the following options:
•EITHER: take at least 1 but not more than 3 of the red pebbles OR: take at least 1 but not more than 2 of the black pebbles.
Which of the players has a winning strategy in normal play? (Hint: Compute the GRUNDY numbers for the red and black piles separately (as in Ex. 2.4) and apply Theorem 2.5.)
_____________________________
1 Also chess computer programs follow this idea.
2 (Much) more can be found in the highly recommended treatise of CONWAY [7].
3 “Minimal excluded”.
4 Recall Theorem 2.2!
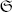 and recall that Γ represents the collection of all possible stages in an abstract sense. Assume that a concrete instance of Γ starts with the initial state σ0 ∈
and recall that Γ represents the collection of all possible stages in an abstract sense. Assume that a concrete instance of Γ starts with the initial state σ0 ∈ 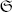 . Then we may imagine that the evolution of the game is caused by two “superplayers” that alternate with the following moves:
. Then we may imagine that the evolution of the game is caused by two “superplayers” that alternate with the following moves: , we assume
, we assume and two players L and R and an initial element G0 ∈
and two players L and R and an initial element G0 ∈ 
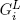 or by R to a game
or by R to a game 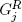 , depending on whose turn it is to make a move.
, depending on whose turn it is to make a move.




 of all combinatorial games can be created systematically. We first observe that there
of all combinatorial games can be created systematically. We first observe that there