 that is in a state σ with probability πσ. Then
that is in a state σ with probability πσ. Then  has the entropy
has the entropyPotentials and Temperature
The temperature of a system depends on the measuring device in use, which is mathematically represented as a potential function. BOLTZMANN’s approach to the notion of temperature in statistical thermodynamics extends to general systems. Of particular interest are n-person matrix games where the temperature reflects the activity of the player set as a whole with respect to the total utility. The interpretation of the activity as a METROPOLIS process moreover indicates how the strategic decisions of individual players influence the expected value of the measuring device.
Consider a finite system  that is in a state σ with probability πσ. Then
that is in a state σ with probability πσ. Then  has the entropy
has the entropy

The expected value of a potential υ ∈ ℝ will be
will be

Let us think of υ as a numerical measuring device for a certain characteristic feature of  . In a physical model, the number υσ could describe the level of inherent “energy” of
. In a physical model, the number υσ could describe the level of inherent “energy” of  in the state σ, for example. In economics, the function υ :
in the state σ, for example. In economics, the function υ :  → ℝ could be a representative statistic for the general state of the economy. In the context of an n-person game, υσ could possibly measure a degree of “activity” of the set N of players in the state σ, etc.
→ ℝ could be a representative statistic for the general state of the economy. In the context of an n-person game, υσ could possibly measure a degree of “activity” of the set N of players in the state σ, etc.
Of course, the activity level υσ depends on the particular characteristic feature that is investigated under υ. Different features of  may display different activity levels in the same state σ.
may display different activity levels in the same state σ.
1. Temperature
If the expected value μ = E(υ, π) is a measure for the degree of activity of  relative to the probability distribution π and the potential υ, there may nevertheless be other probability distributions π′ with the same expected value
relative to the probability distribution π and the potential υ, there may nevertheless be other probability distributions π′ with the same expected value

The idea is now to derive a canonical probability distribution β with a given expected value μ. To this end, we select β as the distribution with the largest entropy:

As it turns out (Lemma 7.1 below), every other probability distribution π yielding the same expected value μ of υ will have a strictly smaller entropy H(π) < H(β), which means that its specification would require more information. In this sense, β is the unique “freest” (i.e., least biased) distribution with expectation μ.
1.1.BOLTZMANN distributions
Given the potential υ :  → ℝ with values υσ = υ(σ), any t ∈ ℝ defines a related BOLTZMANN1 (probability) distribution β(t) on
→ ℝ with values υσ = υ(σ), any t ∈ ℝ defines a related BOLTZMANN1 (probability) distribution β(t) on  with the components
with the components

REMARK 7.1. The distributions β(t) are also known as BOLTZMANN-GIBBS2 distributions. The function Z(t) is the associated so-called partition function.
Computing derivatives, one finds3 that the expected value of υ relative to b(t) can be expressed as the logarithmic derivative of the partition function:

NOTA BENE. Under a BOLTZMANN distribution β(t) with t ∈ ℝ, no state of  will be impossible (i.e., occur with probability 0) and no state will occur with certainty (i.e., with probability 1) if
will be impossible (i.e., occur with probability 0) and no state will occur with certainty (i.e., with probability 1) if  has more than one state.
has more than one state.
In the special case t = 0, one has Z(0) = | |. So β(0) is the uniform distribution on
|. So β(0) is the uniform distribution on  with the average potential value as its expectation:
with the average potential value as its expectation:

Moreover, one observes the limiting behavior

In fact, one finds that any value μ between the minimum and the maximum of υ can be achieved as the expected value relative to a unique BOLTZMANN distribution. Moreover, the BOLTZMANN distribution is the one with the largest entropy relative to a prescribed expected value:
LEMMA 7.1. Let υ∗ = minσ∈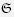 and υ* = maxσ∈
and υ* = maxσ∈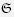 υσ. Then:
υσ. Then:
| (0) | υ* = υ* ⇒ μ(t) = υ*(= υ*) holds for all t ∈ ℝ. |
| (1) | For every υ* < μ < υ*, there exists a unique t ∈ ℝ such that μ = μ(t). |
| (2) | H(π) < H(β(t)) holds for every probability distribution π ≠ β(t) on  mit expectation E(υ, π) = μ(t). mit expectation E(υ, π) = μ(t). |
From Lemma 7.1, it is clear that one could characterize the expected value μ of a non-constant potential υ equally well by specifying the parameter t ∈ ℝ ∪ {−∞, +∞} of the BOLTZMANN distribution β(t) with expectation

In analogy with the BOLTZMANN model in statistical thermodynamics for the temperature, we call the related parameter

the temperature of the system  relative to a potential with the expected value μ(1/T). Adjusting the notation accordingly to
relative to a potential with the expected value μ(1/T). Adjusting the notation accordingly to

the BOLTZMANN distribution β(T) has the coefficients

As the system “freezes” to the temperature T = 0, one obtains the extreme values of the potential υ as the expectations in the limit, depending on whether the limit 0 is approached from the positive or the negative side:

In contrast, all states of  are equally likely at when the temperature T is infinite.
are equally likely at when the temperature T is infinite.
METROPOLIS et al. [29] have pointed out that BOLTZMANN distributions may result dynamically as limiting distributions of quite general stochastic processes.
To formulate the process, we associate with each σ ∈  a neighborhood
a neighborhood 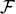 (σ) ⊆
(σ) ⊆  that renders
that renders  connected in the following sense:
connected in the following sense:
•For any σ, τ ∈  , there are σ1, . . . , σk ∈
, there are σ1, . . . , σk ∈  such that
such that

where σ0 = σ and σk+1 = τ.
The METROPOLIS process specifies a parameter t ∈ ℝ and proceeds from an initial state σ0 in a (possibly infinite) sequence of state transitions relative to the potential υ in the following way.
When the process has reached the state σ, a neighbor τ ∈ 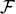 (σ) is selected at random as a candidate for a transition σ → τ and then proceeds as follows:
(σ) is selected at random as a candidate for a transition σ → τ and then proceeds as follows:
(1)If υτ ≥ υσ, then the transition σ → τ is made with certainty, i.e., with probability

(2)If υτ < υσ, then the transition σ → τ is made with probability

and repeated otherwise. Hence the transition selection procedure is repeated with probability 1 − αστ.
It follows that the METROPOLIS state transitions define a MARKOV chain4 on  with transition probabilities
with transition probabilities

The METROPOLIS process converges as a MARKOV chain to a limiting distribution on  under quite general conditions. A sufficient condition is, for example:
under quite general conditions. A sufficient condition is, for example:
PROPOSITION 7.1. Assume that all neighborhoods 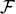 (σ) have the same size f = |F(σ)|. Then the METROPOLIS process converges to the BOLTZMANN probability distribution β(t) in the limit.
(σ) have the same size f = |F(σ)|. Then the METROPOLIS process converges to the BOLTZMANN probability distribution β(t) in the limit.
In other words: The process will arrive at the state σ ∈  after n iterations with probability
after n iterations with probability

Proof. By Ex. A.12 of Section 7 of the Appendix, it suffices to check that the condition

is satisfied by any σ, τ ∈  . So assume υτ < υσ, for example. Then
. So assume υτ < υσ, for example. Then

Simulated annealing. The METROPOLIS process suggests a simple intuitive method for maximizing a function υ : X → ℝ over a finite set X:

There is no guarantee that the simulating annealing heuristic will find a maximizer of υ. However, the analogy with the METROPOLIS procedure makes it intuitively plausible that the method might generate elements xn with the property

The schematic description of the simulated annealing heuristic leaves many implementation details vague. For example:
•What is the best neighborhood structure in (S0)?
•How should the numbers t0, t1, . . . in (S1)be chosen best?
Nevertheless, the method often produces quite good results in practice5 and has become a standard in the tool box for discrete optimization problems.
REMARK 7.2. The terminology “annealing” (= cooling) derives from the interpretation of the related parameters Tn = 1/tn as temperatures which simulate a cooling schedule Tn → 0.
REMARK 7.3. The import of the simulated annealing method is not so much the generation of BOLTZMANN distributions at fixed temperature levels but the convergence of the expected potential values μ(t) to the extremum:

The latter property can be guaranteed under much more general conditions than are formulated in Proposition 7.1.6
3.Temperature of matrix games
Let Γ = Γ(ui | i ∈ N) be an n-person game with player set N = {1, . . . , n} where each player i ∈ N has a finite set Xi of strategic resources and a utility function

In the model of randomized matrix games, it is assumed that the players i choose probability distributions π(i) on their strategy sets Xi independently from each other and then select elements xi ∈ Xi according to those distributions.
Let us drop the stochastic independence assumption and consider the more general model where the joint strategy

would be chosen by the player set N with a certain probability πx. The aggregated total utility value is then expected to be

The players’ total utility

is a potential on  . So one may consider the (BOLTZMANN) temperature relative to u. In the case
. So one may consider the (BOLTZMANN) temperature relative to u. In the case

we say that Γ is is played at temperature T. If |T| ≈ ∞ (i.e., |T| is very large), we expect about the average value of the total utility:

If T > 0 is very small (i.e., T ≈ 0), then we may expect about the maximal total utility:

Similarly, if T ≈ 0 and T < 0 holds, about the minimal total utility value is to be expected:

A METROPOLIS model. In order to model the dynamic behavior of the player set N as a METROPOLIS process, define the set

A selection (i, y) ∈ 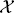 , when the game is in the state x ∈
, when the game is in the state x ∈  , corresponds to a possible transition
, corresponds to a possible transition

with the interpretation that player i considers the alternative strategy y ∈ Xi as a candidate for an exchange against the current xi ∈ Xi. Hence, if (i, y) is chosen randomly, the probability for the corresponding transition is

So each x ∈  has the same number f = |
has the same number f = | | of neighbors. Clearly, this neighborhood structure is connected. Hence Proposition 7.1 shows that the process converges to a BOLTZMANN probability distribution:
| of neighbors. Clearly, this neighborhood structure is connected. Hence Proposition 7.1 shows that the process converges to a BOLTZMANN probability distribution:

Recall that every state x occurs with strictly positive probability in a BOLTZMANN distribution at temperature T ≠ 0. So we should not expect convergence towards an equilibrium with respect to u.
This observation does not contradict the guaranteed existence of an equilibrium in the randomized version of a matrix game (Theorem 6.1). The reason can be found in the different roles of the players in the models:
(1)In a randomized matrix game, each player i ∈ N chooses, individually, a probability distribution π(i) for the selection a xi ∈ Xi with the goal of optimizing the individual utility ui.
(2)In the METROPOLIS process, the total utility u of the group N of players is the key objective.
REMARK 7.4 (Social justice). It appears to be in the joint interest of the community N of players to play Γ at a temperature T that is close to 0 but positive if a large total utility value is desired and negative if a minimal value is sought.
The potential function u is equivalent (up to the scaling factor n) to the average utility function  of the members of N:
of the members of N:

A high group average does not necessarily imply a guaranteed high utility value for each individual member in N, however.
To formulate it bluntly:
•Even when a high average utility value is used as a criterion for “social justice” in N, there may still be members of N that are not treated “fairly”.
The interplay of different interests (individual utility of the players vs. combined utility of the set of all players) is studied in more details within the framework of cooperative games in Chapter 8.
_____________________________
1 L. BOLTZMANN (1844–1906).
2 J.W. Gibbs (1839–1903).
3 See also Section 6 of the Appendix.
4 See Section 7 in the Appendix.